MARS-like Feistel 结构的量子攻击
钱 新, 尤启迪, 周 旋, 张 洋, 赵晓晶
1. 北京卫星信息工程研究所 信息科学工程技术中心, 北京 100086
2. 清华大学 计算机科学与技术系, 北京 100084
1 引言
Feistel 结构[1]自1973 年由Feistel 等人提出之后便成为了分组密码设计的主流整体结构. Feistel 结构具备相似的加解密操作, 轮函数的选择也较为灵活多变, 很多广泛应用的分组密码, 如DES、Camellia、FEAL、RC5 等都采用了Feistel 结构.
广义Feistel 结构(generized Feistel structure, GFS) 是对Feistel 结构的一般形式的推广, 可以随着分支数的增加以更小规模的轮函数实现更大的分组, 从而在设计轻量级分组密码时具备比Feistel 结构更大的优势, 更适用于资源受限的通信环境中. 在1989 年美密会上, Zheng 等人[2]总结了三类广义Feistel结构, 分别为Type-1 型、Type-2 型和Type-3 型广义Feistel. 随后Schneier 等人[3]将Feistel 结构推广到了非平衡Feistel 结构, 此后出现了各种各样的广义Feistel 结构以及相应代表性的分组密码, 包括CAST 256-like Feistel 结构(Type-1)[4], CLEFIA-like Feistel 结构(Type-2)[5], SMS4-like Feistel 结构[6], MARS-like Feistel 结构[7]. MARS-like Feistel 结构是在AES 候选密码MARS 分组密码的基础上定义的一种广义Feistel 结构. Moriai 等人[7]在2000 年给出了MARS-like 广义Feistel 结构的随机性证明, 并提出5 轮4 分支MARS-like Feistel 结构具有伪随机性, 8 轮4 分支MARS-like 结构具有超伪随机性; 当分支数为d时,d+1 轮MARS-like 结构具有伪随机性, 2d轮MARS-like 结构具有超伪随机性. 对于MARS-like 结构的密码性质研究主要集中在不可能差分分析. 目前最好的结果是, 当分支数(子块数)d为偶数时, 可以构造长为3d −1 轮的不可能差分特征, 而当d为奇数时, 可以构造任意长轮数的不可能差分特征.
随着量子理论的发展迅速, 量子信息科学的发展为密码学的发展也带来了一定挑战. 后量子密码成为了密码学的研究热点. 量子计算机的出现意味着人类计算能力的上限又得到极大的提升. Grover 提出了一种无序数据库的标准搜索算法, 以Grover 算法[8]为代表的量子搜索算法以及推广算法在量子计算环境下的计算复杂度是对经典算法的平方加速, 可用于加速密钥的搜索, 对所有密码产生了一定威胁; Shor算法[9,10]可用于分解大整数、求解离散对数, 在在量子计算环境下的计算复杂度是对经典算法的指数加速, 可用于相关公钥密码中的数学难题的加速求解, 对RSA、ECC 等为代表的公钥密码产生了一定威胁.相比于公钥密码, 由于对称密码算法通常不具有明显的代数结构, 对称密码方案的设计也并非基于相应数学难题的计算困难性, 在一段时间内, 密码学界的普遍观点是, 针对对称密码没有明显有效的量子攻击方法. 这种观点在2010 年之后被Simon 算法[11]在量子区分攻击Feistel 结构中的应用, 以及Simon 算法与Grover 算法的结合在量子密钥恢复攻击中的应用打破. Kuwakado 和Morii[12]首先利用Simon 算法构造了3 轮Feistel 结构的多项式时间量子区分器. 随后, Even-Mansour 算法的量子密钥恢复攻击[13]、各种MAC 算法的伪造攻击[14]、AEZ 的量子破解[15]、FX 结构的密钥恢复攻击[16], 以及Feistel 结构的量子密钥恢复攻击[17–21]和量子安全性证明[22]等相继被提出. 广义Feistel 结构的量子分析首先由Dong 等[23]提出并给出了Type-1、Type-2 广义Feistel 结构的量子区分攻击以及密钥恢复. 随后倪博煜等[24,25]和罗宜元[26]对相关结果进行了改进. 对SMS4-like 广义Feistel 结构以及SMS4 算法的量子安全性分析由钱新等[27]提出.
需要指出的是, 考虑到针对对称密码进行量子分析时的攻击者具备的不同攻击能力, 可分为量子选择明文攻击和量子选择密文攻击[28]. 此外根据Zhandry[29]的研究工作, 分组密码的量子分析模型主要有两种: 标准安全模型、量子安全模型. 两种分析模型的区别在于: 在标准安全模型中, 攻击者对预言机的查询只能通过经典方法进行, 对数据的处理可以使用量子计算机; 在量子安全模型中, 攻击者对预言机的查询可以以量子叠加态的方式进行, 并获得相应的输出叠加态, 对数据的处理也可以使用量子计算机.
本文基于量子安全模型, 结合Simon 算法和Grover 搜索算法, 给出了MARS-like 广义Feistel 结构的量子选择明文攻击(quantum chosen-plaintext attack,QCPA)和量子选择密文攻击(quantum chosenciphertext attack, QCCA). 在量子选择明文攻击条件下, 给出d分支MARS-like 结构的d轮多项式时间量子区分攻击, 以及2d轮量子密钥恢复攻击; 在量子选择密文攻击条件下, 给出d分支MARS-like 结构的d+1 轮多项式时间量子区分攻击, 以及2d+1 轮量子密钥恢复攻击.
2 预备知识
2.1 Simon 算法
Simon 问题: 给定一个布尔函数f:{0,1}n →{0,1}n, 该布尔函数f满足Simon 承诺, 即满足x ⊕y={0n,s} ⇔f(x) =f(y). 求出n比特的s使得布尔函数f满足Simon 承诺的问题即为Simon 问题. 在经典计算环境下, 利用生日攻击解决这个问题的时间复杂度约为O(2n2). Simon 算法[11]由Simon 于1994 年提出, 主要用于解决Simon 问题——求解特殊布尔函数f的周期. 在量子计算环境下, 利用Simon 量子算法可以对布尔函数f以O(n) 的时间复杂度求出周期s.
Simon 算法包括以下步骤:
(1) 初始化: 将2n个量子比特的寄存器的状态初始化为|0〉⊗n|0〉⊗n, 将Hadamard 变换应用于前n个量子比特得到平均叠加态
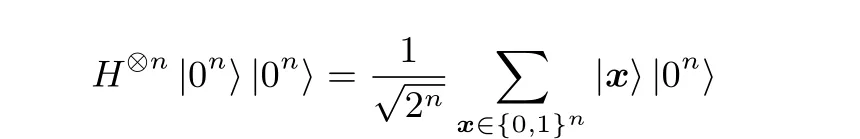
(2) 对量子预言机Uf:Uf|x〉|b〉=|x〉|b ⊕f(x)〉, 进行量子询问得到当前的状态
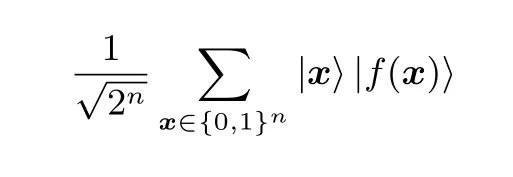
(3) 测量后n个量子比特, 前n个量子比特塌缩为状态
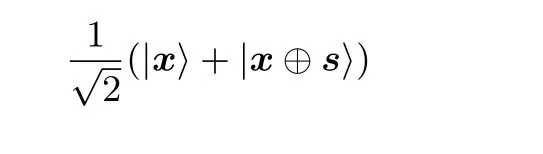
(4) 将Hadamard 变换应用于前n个量子比特得到状态
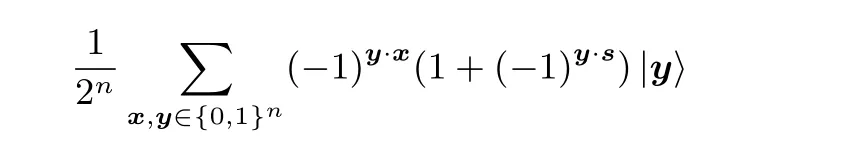
(5) 测量前n个量子比特, 显然该叠加态中满足y·s=1 则|y〉的振幅为0, 即
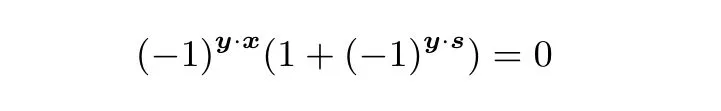
因此, 测量所有|y〉都必然满足y·s=0.
重复以上步骤O(n) 次, 即可得到函数f的周期s.
Simon 算法对应的操作可以简单描述为
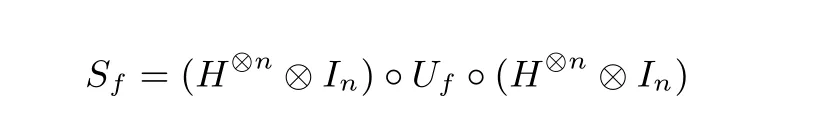
Simon 算法的整个过程可以表示为
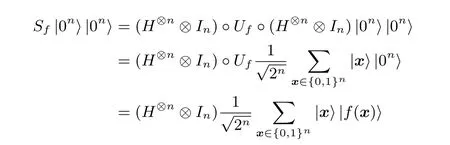
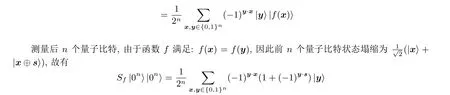
测量前n个量子比特, 所得|y〉满足y·s= 0. 重复以上步骤O(n) 次, 可以得到n −1 个线性无关方程组成方程组, 求解该线性方程组即可得到函数f的非零周期s.
需要指出的是, 参考Santoli 等人[18]提出在构建区分器进行密钥恢复攻击时, 无需真正计算得到函数f的周期s, 通过运行Simon 算法
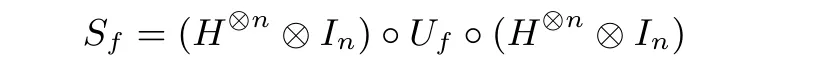
得到满足y·s=0 的, 对应n −1 个线性无关方程组的向量|y1〉,|y2〉,|y3〉,···所张成的空间的维数. 如果函数f存在非零周期s, 也就意味着方程组y·s=0 存在非零解, 则向量|y1〉,|y2〉,|y3〉,···所张成的空间的维数至多为|s|−1; 如果函数f不存在任何周期, 也就意味着方程组y·s=0 不存在非零解, 则向量|y1〉,|y2〉,|y3〉,···所张成的空间的维数将可以达到|s|. 因此无需真正计算得到函数f的周期s, 即使函数f存在几个局部周期, 或是周期不等于s的情况下, 仍可以通过检查空间维数来验证函数f的周期性.
2.2 Grove 算法

(1) 初始化: 将n量子比特的初始状态设置为|0〉⊗n, 将Hadamard 变换应用于n量子比特得到相应的叠加态|φ〉
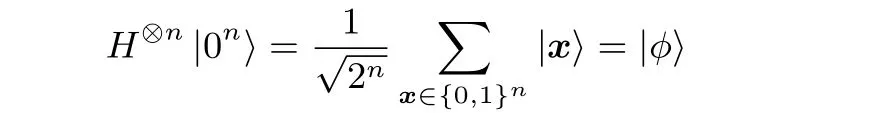

其中Grover 迭代包括以下几个步骤:
(1) 翻转目标态|x0〉的相位, 其余态保持不变
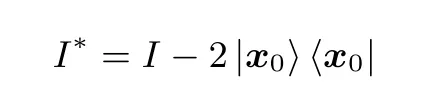
对目标态的相位反转是通过查询量子预言机Of来完成的;
(2) 进行n量子比特Hadamard 变换H⊗n;
(3) 保持|0〉态的相位不变, 翻转其余态的相位
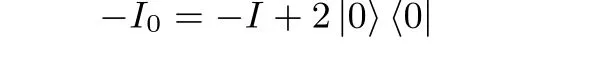
(4) 进行n量子比特Hadamard 变换H⊗n.
其中后面三步称为扩散操作.
Grover 迭代对应的操作可以简单描述为
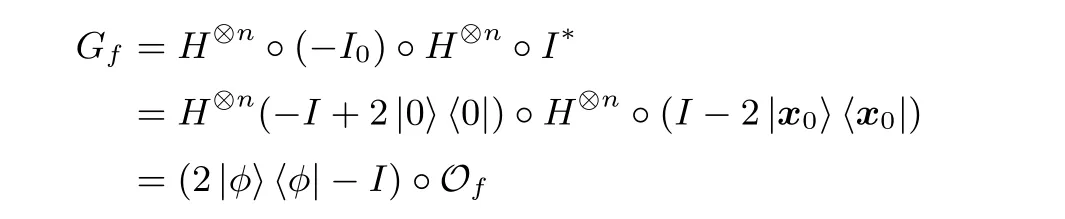
2.3 量子密钥恢复攻击
Leander 等人于2017 年提出对FX 结构的量子密钥恢复攻击[16],该FX 结构满足Enc(x)=Ek0(x+k1)+k2,通过构造函数f(k,x)=Enc(x)+Ek(x)=Ek0(x+k1)+k2+Ek(x),若猜测的密钥正确,k=k0,满足f(k,x)=f(k,x+k1). 若猜测的密钥错误,k ̸=k0, 不存在f(k,x)=f(k,x+k1),f(k,·) 不是周期的. Leander 等人在量子选择明文条件下结合Simon 算法和Grover 算法来实施对FX 结构的量子攻击.
本文分别在量子选择明文条件和量子选择密文条件下, 基于Simon 算法给出MARS-like 结构的具有多项式时间的量子区分器, 并基于Grover 算法结合Simon 算法对MARS-like 结构进行相应的量子密钥恢复攻击.
3 QCPA 条件下对MARS-like 结构的量子攻击
MARS 密码算法是AES 加密标准的五个最终候选算法之一, 其分组长度为128 比特, 包括四个分支, 采用非平衡Feistel 结构, 轮函数fi的输出长度大于输入长度. 其主要带密钥变换部分, 也称密码核(cryptographic core), 每轮中使用一个子块作为轮函数的输入, 得到三个32 比特的输出, 分别和其他三个子块相加或者异或, 因而每轮变换中作为轮函数输入的一个子块以及轮密钥将影响到其他所有子块. 在密码核的前后分别是前向混合层和后向混合层. MARS-like 结构在MARS 密码算法的密码核的基础上做了简化, 其轮函数的输出与其他分支之间均采用异或运算, 并且省略了作为轮函数输入的子块的移位变换,与MARS 密码算法四个分支相比MARS-like 结构还可以有更多的分支.

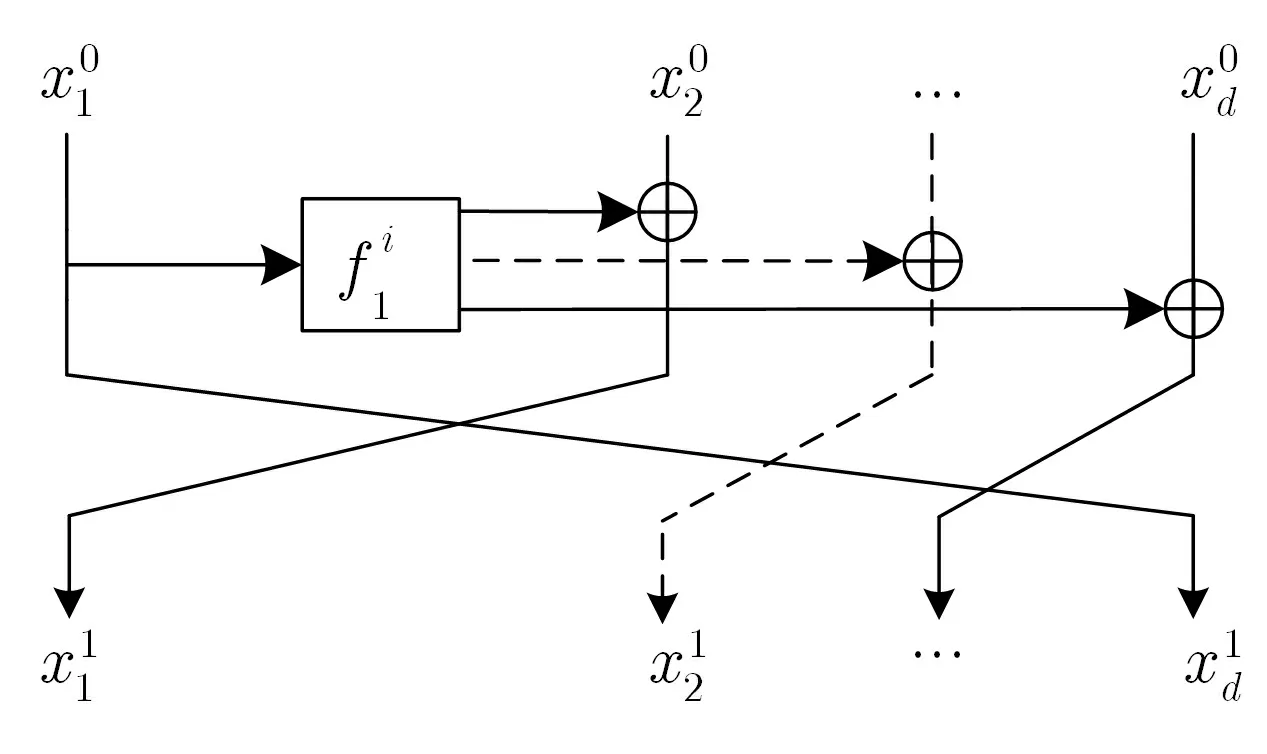
图1 1 轮d 分支MARS-like 结构Figure 1 Structure of 1-round MARS-like of d branches
下面本文将先以四分支MARS-like 结构分别给出量子选择明文条件和量子选择密文条件下的具体量子攻击过程, 并推广到针对d分支MARS-like 结构的量子攻击.
3.1 QCPA 条件下的量子区分攻击
对四分支MARS-like 结构构造得到周期函数f如下:
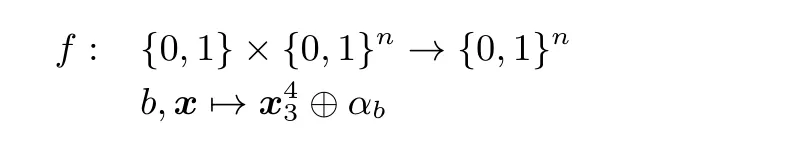

下面验证函数f为周期函数并求得其周期T.

当s=f3(f2(f1(x0)⊕x1)⊕f1(x0)⊕α0)⊕f3(f2(f1(x0)⊕x1)⊕f1(x0)⊕α1) 时, 显然有f(0,x)=f(1,x ⊕s), 因此验证得到函数f满足Simon 承诺, 具有周期T=1||s.
借助周期函数f构造具有多项式时间的4 轮量子区分器如图2 所示.
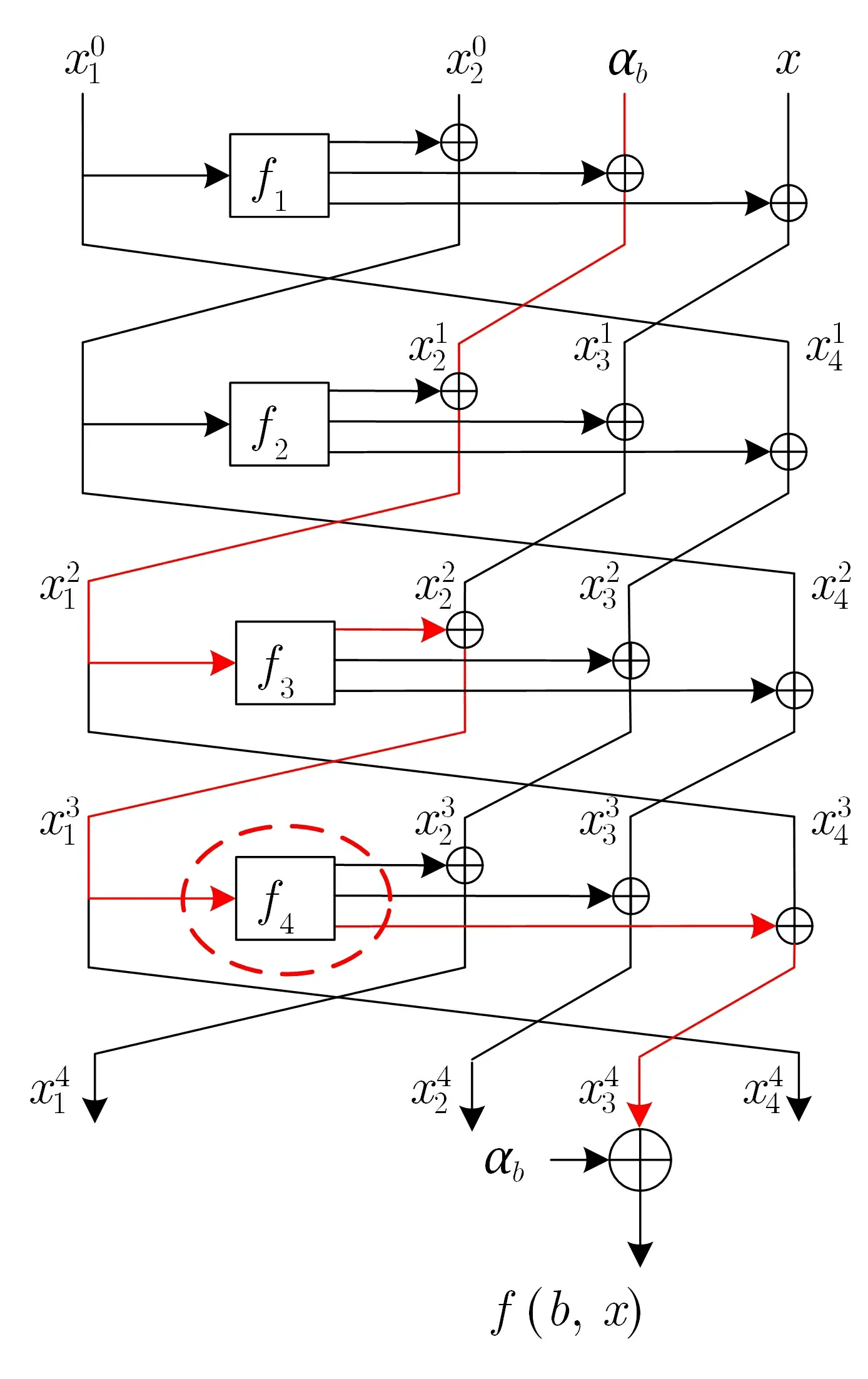
图2 四分支MARS-like 结构的4 轮量子区分器Figure 2 4-round quantum distinguisher on MARS-like of 4 branches
推广至一般情形, 对d分支MARS-like 结构构造得到周期函数f如下:
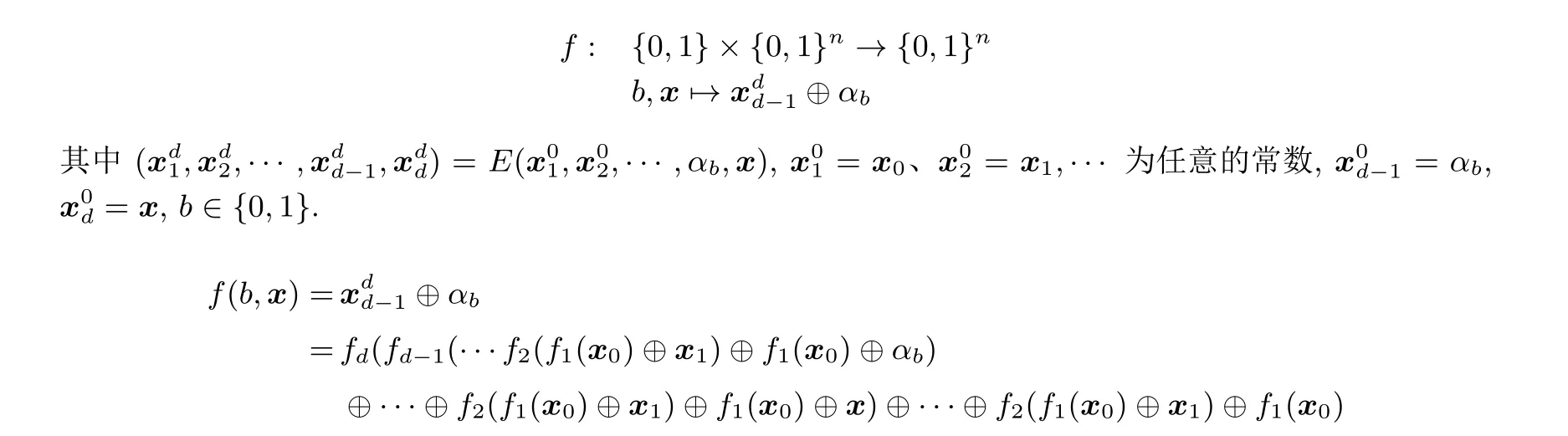
类似地可验证函数f为周期函数并求得其周期T=1||s, 其中
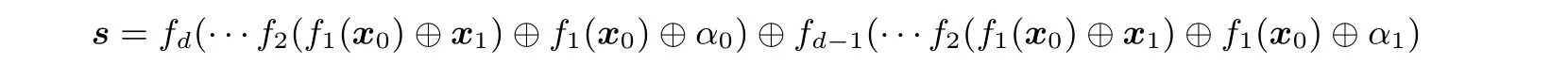
借助周期函数f构造可具有多项式时间的d轮量子区分器, 进行量子区分攻击.
3.2 QCPA 条件下的量子密钥恢复攻击

8 轮量子密钥恢复攻击如图3 所示.
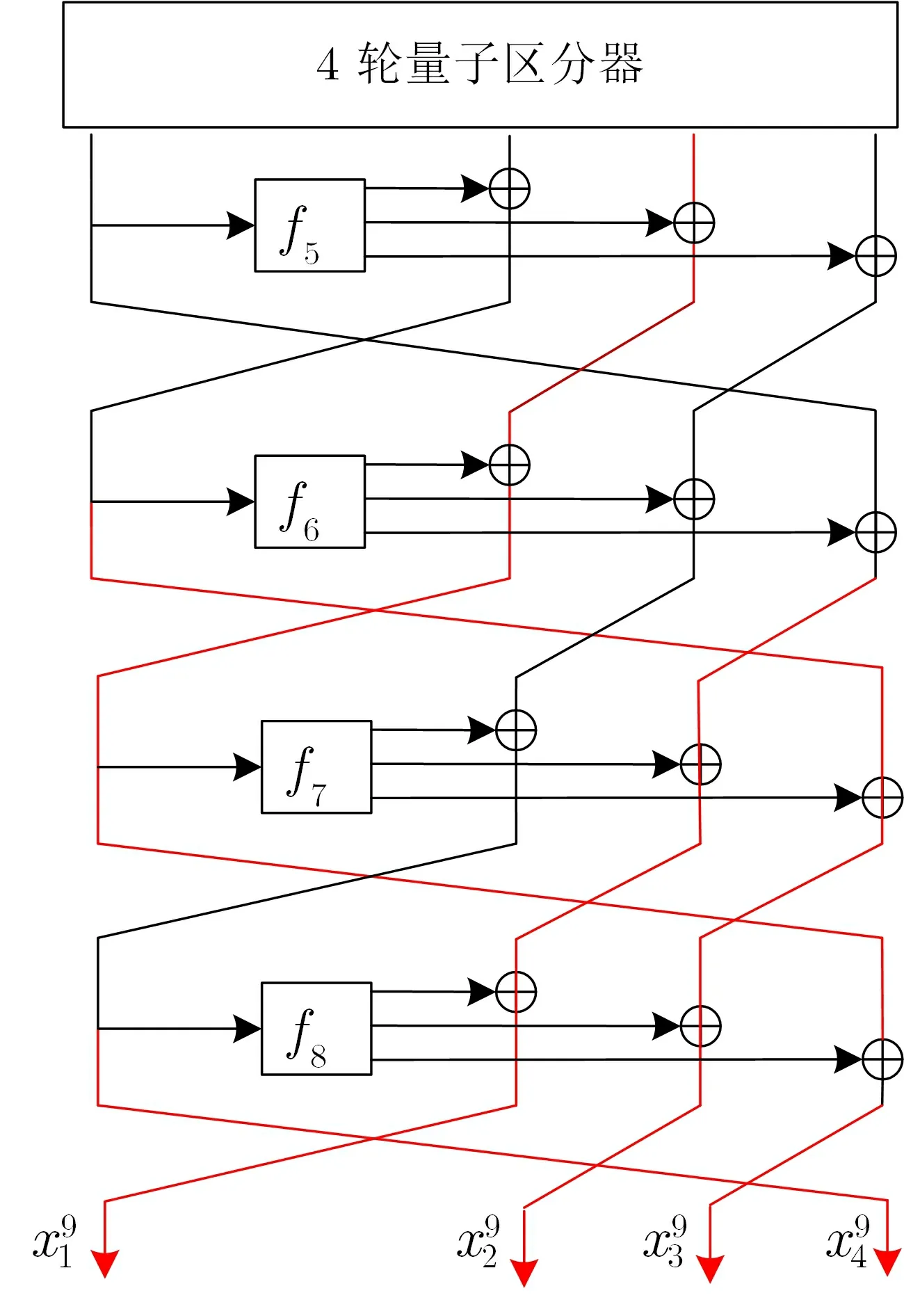
图3 四分支MARS-like 结构的8 轮量子密钥恢复攻击Figure 3 8-round quantum key recovery attack on MARS-like of 4 branches
利用量子区分器进行r轮量子密钥恢复攻击过程如下:


整体攻击架构如图4 所示.
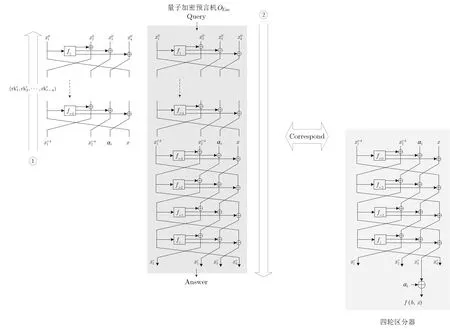
图4 整体攻击架构Figure 4 Construction of quantum attack

4 QCCA 条件下对MARS-like 结构的量子攻击
和QCPA 条件中不同的是, 在QCCA 条件下敌手不仅可以询问量子加密预言机, 还可以访问量子解密预言机.
4.1 QCCA 条件下的量子区分攻击
对四分支MARS-like 结构构造得到周期函数f如下:

当s=α0⊕α1时, 有f(0,s)=f(1,x ⊕s), 验证得到函数f满足Simon 承诺, 具有周期T=1||s.借助周期函数f构造具有多项式时间的5 轮量子区分器如图5 所示.
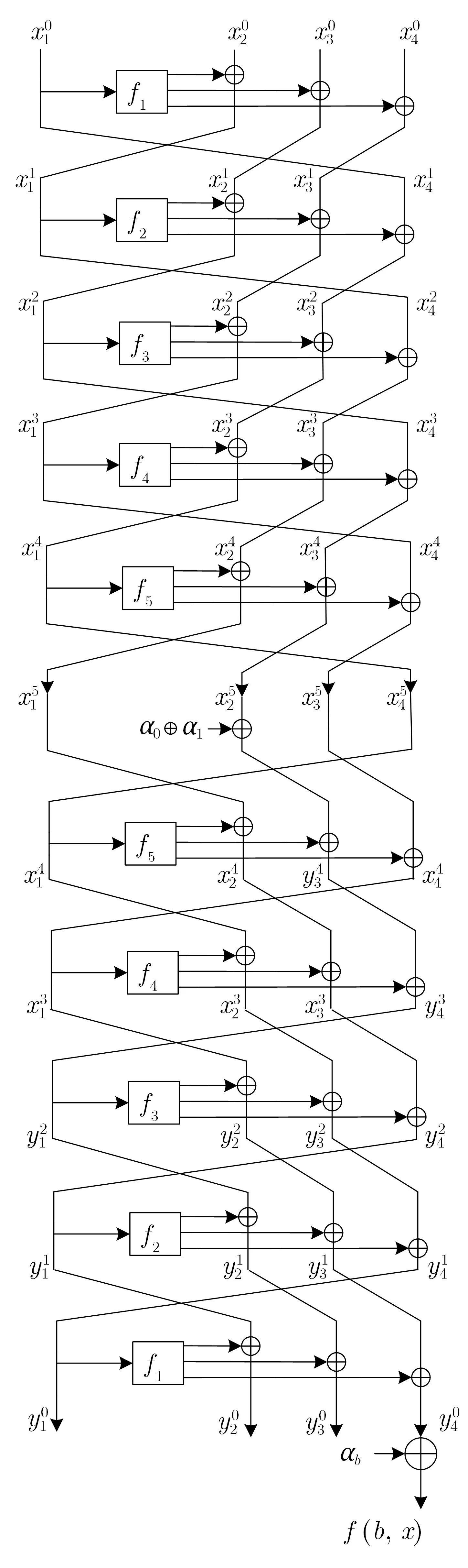
图5 四分支MARS-like 结构的5 轮量子区分器Figure 5 5-round quantum distinguisher on MARS-like of 4 branches
推广至一般情形, 对d分支MARS-like 结构构造得到周期函数f如下:


借助周期函数f构造可具有多项式时间的d+1 轮量子区分器, 进行量子区分攻击.
4.2 QCCA 条件下的量子密钥恢复攻击

8 轮量子密钥恢复攻击如图6 所示.
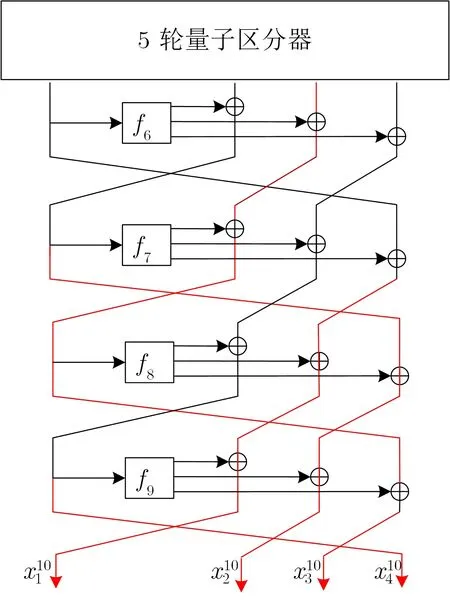
图6 四分支MARS-like 结构的9 轮量子区分器Figure 6 9-round quantum key recovery attack on MARS-like of 4 branches
利用量子区分器进行r轮量子密钥恢复攻击过程如下:


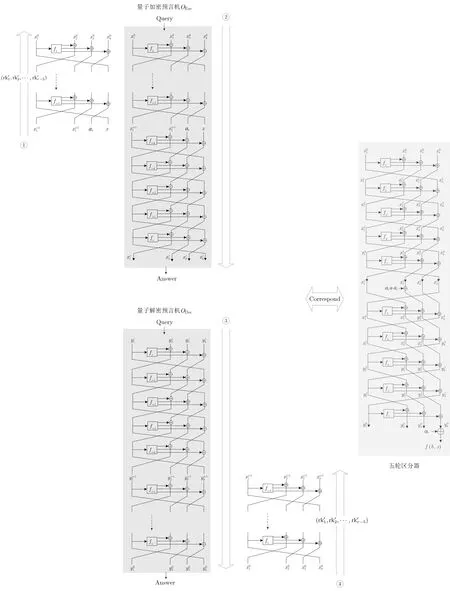
图7 整体攻击架构Figure 7 Construction of quantum attack
5 总结
本文介绍了对MARS-like 结构在量子选择明文条件下以及量子选择密文条件下的量子攻击, 总结了利用Simon 量子算法和Grover 搜索算法对分组密码中的MARS-like 结构进行量子算法攻击的方法. 本文给出了首次对MARS-like 结构的量子算法攻击. 通过利用Simon 算法, 借助周期函数f构建量子区分器, 进行量子密钥恢复攻击. 在量子选择明文条件下, 对四分支MARS-like 结构, 我们在4 轮量子区分器附加4 轮进行8 轮量子密钥恢复攻击; 对d分支MARS-like 结构, 我们在d轮量子区分器附加2d轮进行2d轮量子密钥恢复攻击. 在量子选择密文条件下, 对四分支MARS-like 结构, 我们在5 轮量子区分器附加4 轮进行9 轮量子密钥恢复攻击; 对d分支MARS-like 结构, 我们在d+1 轮量子区分器附加d轮进行2d+1 轮量子密钥恢复攻击.
——日晕

