低开销三进制域Eta 双线性对硬件加速器*

李翔宇

清华大学微电子学研究所北京信息科学与技术国家研究中心, 北京 100084

1 引言

基于身份标识的加密算法(identity-based encryption, IBE) 是一种可以使用任意字符串的公钥密码体制, 它因此不需要公钥证书的发放, 简化了密钥管理和密钥分配, 而且在同等安全级别下, 比其他公钥密码算法有更小的参数, 因而计算速度更快、存储空间更小, 符合以无线传感器网络(wireless sensor network, WSN) 为代表的物联网(internet-of-things, IoT) 应用对低开销安全机制的需求[1]. 我国国家密码管理局发布的商用标识密码算法SM9 就是一种IBE 算法[2]. 双线性对是实现IBE 的关键运算, 在IBE 涉及的各种主要运算中, 它最为耗时[3], 它的性能对IBE 计算的时间有着重要影响. 采用软件方式实现的双线性对难以满足当下网络性能的要求, 因此, 在加密硬件中增加专用的双线性对硬件加速器可以有效地提高IBE 的计算速度和能量利用率.

现有的双线性对硬件加速器设计都是以计算时间为优先考虑的指标, 普遍具有较大的硬件开销或功耗, 并不适用于IoT 节点的应用场景. 鉴于此, 本文开展低开销的双线性对硬件加速器研究, 提出了一种具有更小面积时间积的电路方案.

2 相关研究

用于IBE 的双线性对有早期的Weil[4]对和后来提出的Tate 对[5], 以及基于Tate 对的多种改进的双线性对: 如eta (ηT[6])、ate[7]、reduced ate[8]和optimal ate[9]等. 其中定义在Barreto-Naehrig(BN) 曲线上的Optimal Ate 对计算速度最快, 也是近年研究较多的双线性对, 但是素数域Ate 对的存储开销较大, 不适合应用在WSN 上. 而eta 对因为是对称对, 所以支持更多的协议[10], 而且三进制域GF(3m) 中的乘法及加法电路简单、同等安全性下操作数需要的存储空间要小, eta 对在三进制域上的安全性最高[11], 因此, 三进制eta 对更适合低开销需求的系统, 基于此, 本文选取三进制eta 对的硬件设计进行研究.

在双线性对硬件加速器设计方面, Kömürcü 等人[12]首次实现了Tate 对的ASIC 硬件加速器.Beuchat 等人[13]对三进制域eta 对实现算法进行分析, 提出了无立方根(cube-root-free) 运算算法, 并将Miller 循环进行循环展开, 设计了一个能够运算模乘、立方、累加运算的复合运算模块, 实现了一个更简单的eta 对的FPGA 设计. 此后, Beuchat 等人[14]利用KOM 乘法器(Karatsub-Ofman Multiplier)设计了一个流水线结构的高速eta 对硬件. 2010 年, Beuchat 等[15]又通过对Miller 循环中GF(36m)的稀疏乘法(Sparse Multiplication) 进行优化和调度, 在FPGA 上实现了高效的GF(397)上的eta 对硬件结构. 2012 年, Li 等人[16]设计并实现了800 MHz 的BN 曲线上的optimal Ate 对硬件处理器. 在此基础上, Jun 等人[17]利用高基Montgomery 模乘器提升了该处理器的性能. 在2015 年, Chung 等人[10]设计了全流水的eta 对硬件加速芯片, 成为目前运算速度最快的GF(397)上的eta 对ASIC 硬件加速器.

3 Eta 对和Miller 算法

Eta 对是定义在三进制域GF(3m) 超奇异椭圆曲线y2=x3−x+b上的对称双线性对, 其中参数b ∈{1,−1}. 目前普遍采用的三进制eta 对的计算方法是无立方根的逆向eta 对算法, 如算法1 所示:

算法1 三进制域无立方根的逆向eta 对算法[13]Input: P (xP,yP),Q(xQ,yQ) ∈E(GF(3m))[r], 中间变量t ∈GF(3m),R,S ∈GF(36m)Output: ηT (P,Q)M ∈GF(36m)1 xP = xP +b, yP = −µbyP;2 xQ = x3Q,yQ = y3Q;3 t = xP +xQ;4 R[0] = (yP t −yQσ −yP ρ)·(−t2 +yP yQσ −tρ −ρ2);5 for i = 0 →(m −1)/2 −1 do R[i])3; [1 次GF(36m)立方]7 xQ = x9Q −b,yQ = −y9Q; [4 次GF(3m) 立方]8 t = xP +xQ,u = yP yQ,k = t2; [2 次GF(3m) 乘法]9 S = −k+uσ −tρ −ρ2;10 R[i+1] = R[i] ·S; [1 次GF(36m)乘法]11 end 12 返回RM; [GF(36m)幂运算]6 R[i] =(

其中参数µ满足:

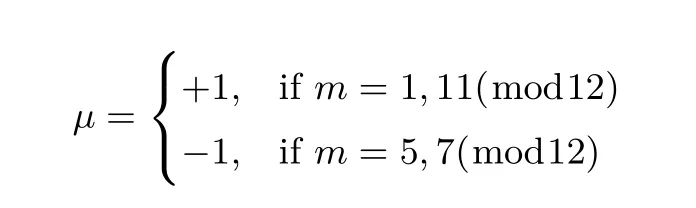
其中R[i]表示第i轮循环得到的R,是GF(36m)中的元素. 其中ρ,σ ∈GF(36m),而且满足ρ3−ρ−b=0和σ2+1 = 0. 由它们构造的集合{1,σ,ρ,σρ,ρ2,σρ2}是有限域GF(36m)关于GF(3m) 的基, 因此可以将R表示为:

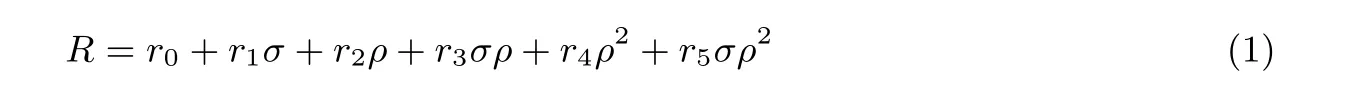
其中ri ∈GF(3m),i=0,··· ,5.

上述算法由两部分组成, 第一部分是Miller 算法和一个M次的最终幂运算(算法1 第12 行). 其中Miller 循环是加速器设计的重点.

4 三进制eta 对硬件加速器设计

4.1 顶层设计

由于幂运算是对Miller 算法的结果进行计算, 并且是由一系列串行的运算来完成的, 其本身以及和Miller 算法之间并没有太大的并行度, 即使增加运算单元, 也不会明显缩短运算周期数. 如果将Miller 运算和幂运算设计在一个电路中, 共用一个数据通路, 则电路在进行幂运算的时候不能完全利用电路中的运算单元, 效率较低. 因此我们将Miller 算法和最后的幂运算分开设计. 考虑到在本文设计中这两个运算时间相当, 我们将Miller 算法和幂运算流水线执行, 这样电路的吞吐率可以提升接近一倍.

而在控制方面, 由于本文的电路规模较大, 并且Miller 算法和幂运算是不同的数据通路, 因此在控制上采用微码控制器来实现: 通过微码单元输出指令来控制数据通路.

4.2 主要运算的硬件电路

4.2.1 GF(3m) 模乘器

GF(3m) 模乘是最主要的基本运算, 本设计采用了字串行的MSE 模乘器(Most-Significant-Element first Multiplier)[18]完成. MSE 模乘器把m位的乘数分解成多个D位的字, 一次用一个字与被乘数相乘, 并进行模多项式f(x) 的运算, 整个m×m位的乘法在k=「m/个周期内完成. 选用字串行方案是因为相比位串行的乘法器结构, 字串行结构更加灵活, 通过选定不同的字长D, 可以实现具有不同面积和速度的模乘器. 为了兼顾电路的面积与速度, 本文选取字长D= 3 进行实现. 得到的m×m位MSE电路结构如图1 所示. 注意: 在电路中每个三进制位使用2 比特信号表示. 其中的乘数B使用2m比特移位寄存器保存, 每个时钟周期向左移2D位(对应D个三进制位), 每一轮运算先由部分积运算电路(图中用乘号表示) 产生D个部分积并移位, 同时模运算单元对上一轮运算的结果取模并移位, 最后将这些结果进行累加. 其中部分积的产生由m个GF(3m) 乘法单元完成.

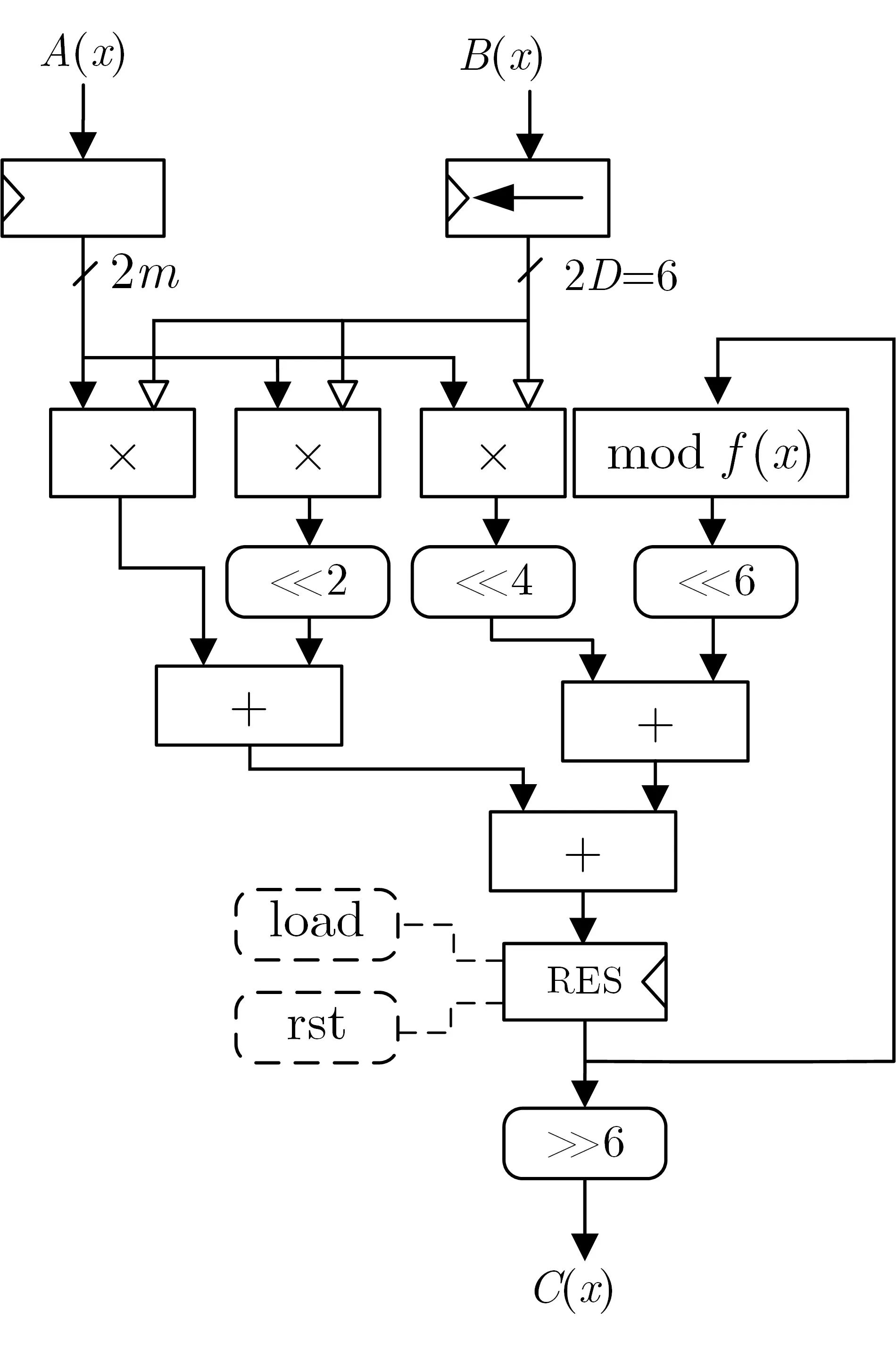
图1 MSE 模乘器结构Figure 1 MSE multiplier

4.2.2 GF(3m) 立方-加法单元

在Miller 算法和最后的幂运算中都需要较多的立方运算. 如果直接用两次GF(3m) 模乘来计算的话开销太大时间也太长. 本文采用文献[19] 的方法—将立方运算用两次GF(3m) 的加法完成, 具体原理不再赘述. 首先将扩域的阶数m表示为m= 3µ+r, 其中µ> 0,r=mmod 3∈{0,1,2}, 然后计算式如式(2)所示. 其核心是计算3 个系数(C0、C1、C2), 它们都是操作数各位的线性组合(如式(3)), 然后通过两次加法进行累加. 在本文设计中根据算法运算规律, 我们将立方运算和加法运算合并构成立方-加法运算单元, 如图2 所示. 这个单元可以完成A3+B的运算, 当B=0 时, 即是立方运算单元; 当左右两个多路选择器分别选择1 和0 时, 即执行A+B.

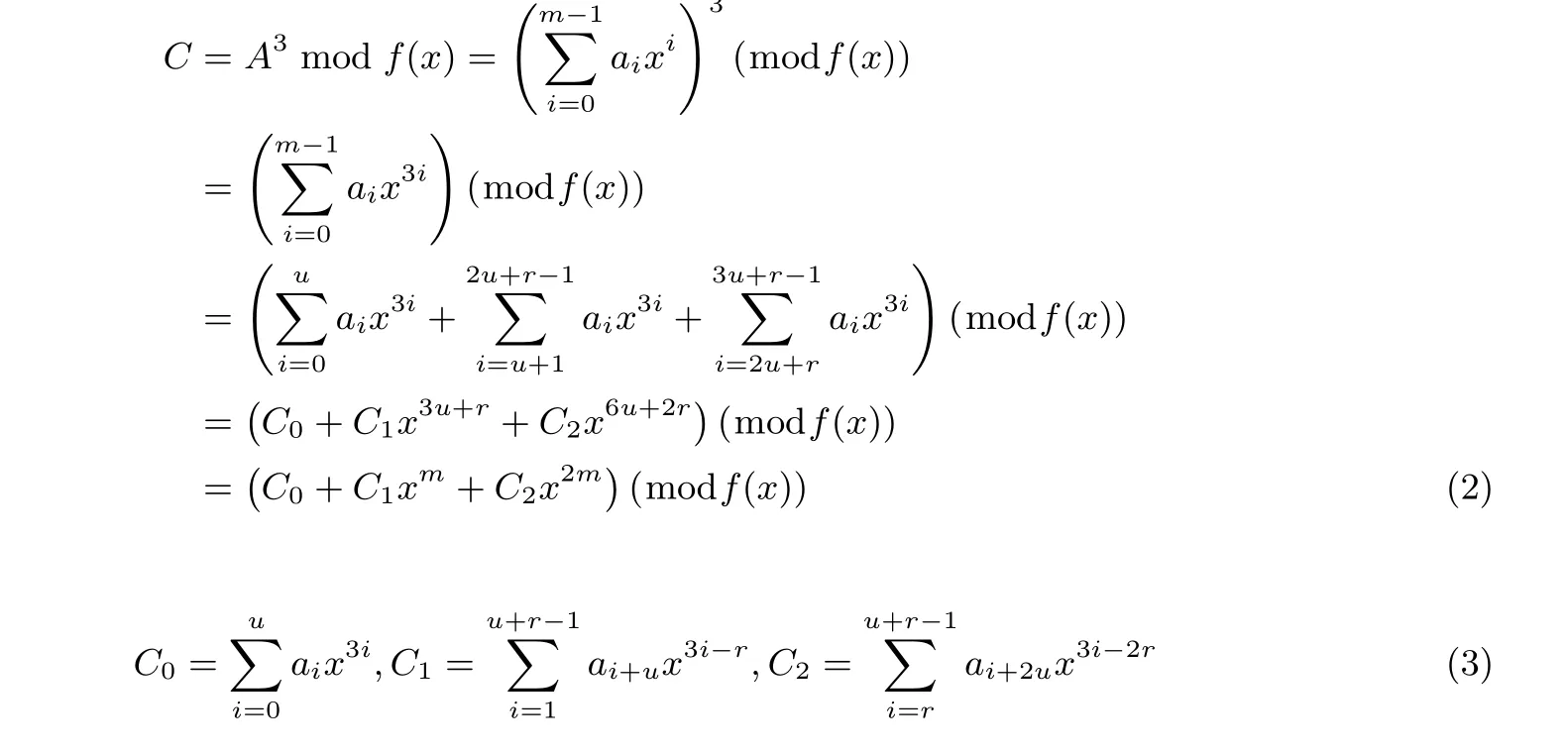
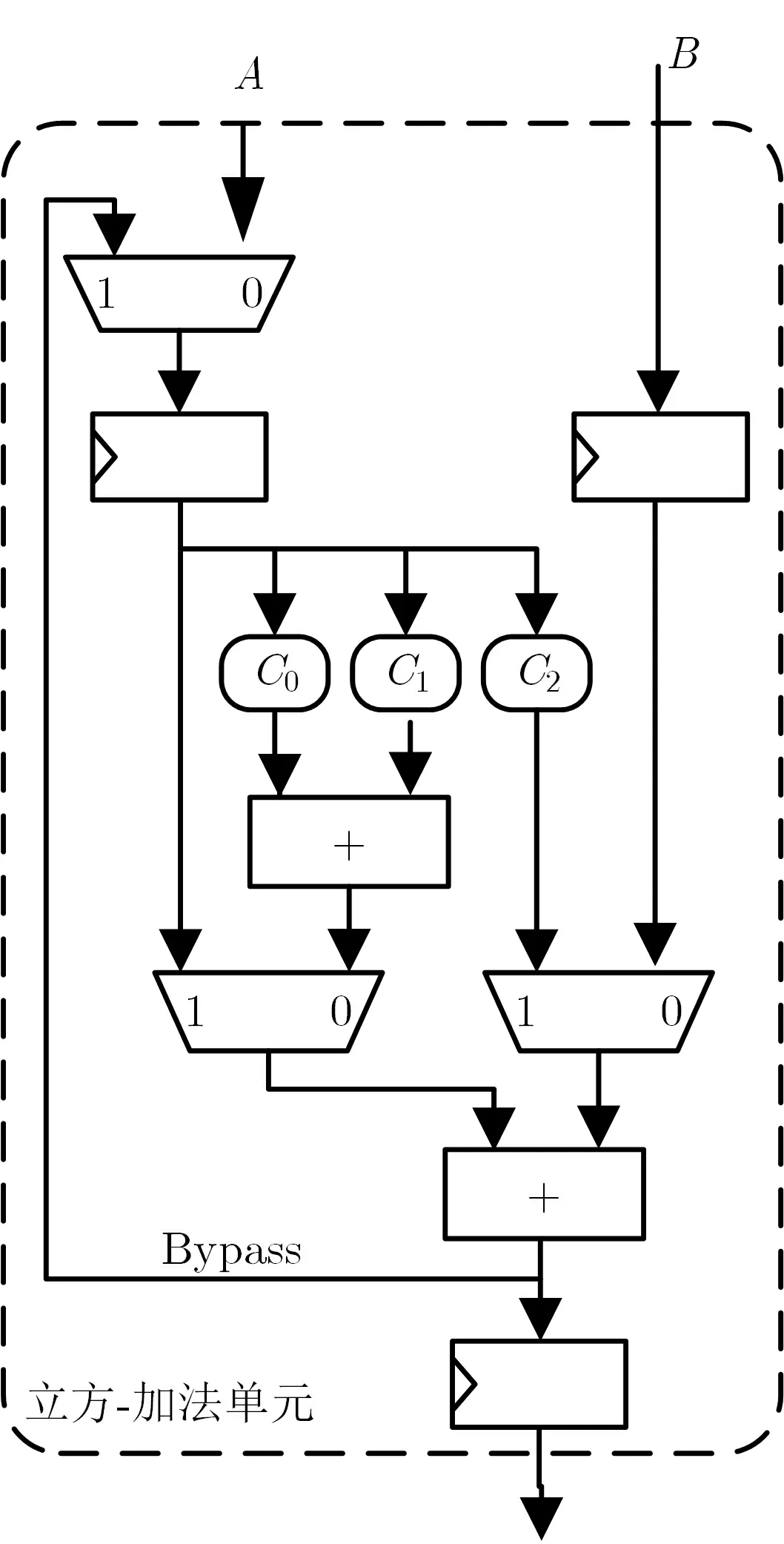
图2 立方-加法单元电路结构Figure 2 Structure of cube-addition unit

4.3 Miller 算法的硬件设计

Miller 循环中的R的迭代乘法(算法1 的第10 行) 是GF(36m)的乘法, 由于多项式S只有4 项非0 系数, 因此该步乘法被称为稀疏乘法. 前人的工作重点普遍是对GF(36m)的稀疏乘法进行优化, 努力减少GF(3m) 模乘运算的次数来降低运算的复杂度. 虽然乘法次数的降低有利于硬件面积的降低, 但是加法次数也在急剧地增加, 而控制逻辑也更加复杂. 为了控制电路规模和功耗, 本文并不一味地追求乘法次数的降低, 而是通过乘法和加法次数之间的平衡, 此外, 考虑到Miller 运算的中间结果具有较大的长度,通常为几百上千比特, 对于运算中间结果的存储和传输开销也进行优化——通过调度尽量减少中间值的存储和传输来提高硬件实现效率, 比如让各个运算之间共享操作数.

4.3.1 算法调度与优化

首先, 我们把GF(36m)的立方与稀疏乘法(算法1 的第6 行与第10 行) 结合起来进行优化, 寻求更大的并行度和可共享的操作, 整合后的Miller 循环运算式变为:

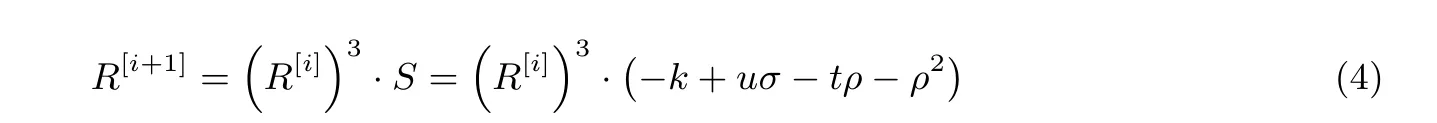
为了直观表达运算结果, 先定义中间变量:

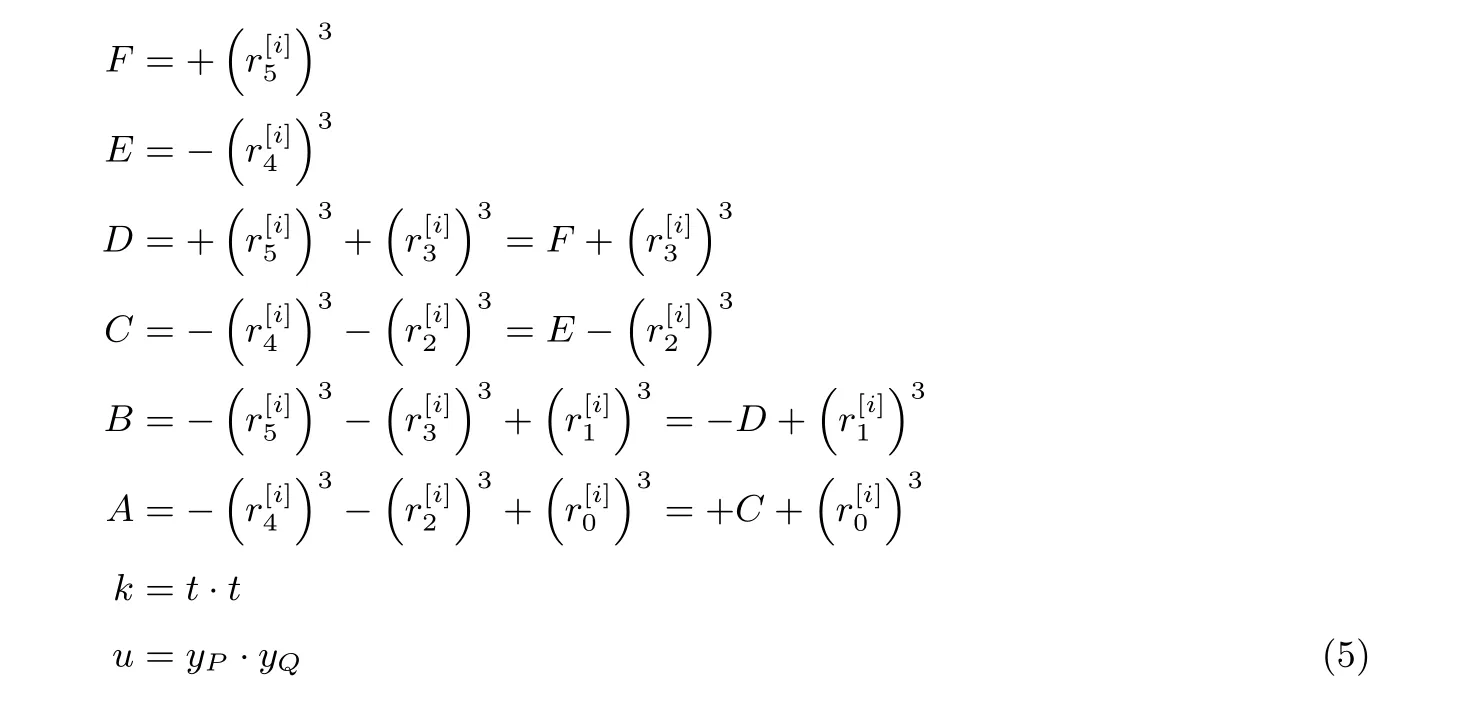
并定义A′=−A −E,B′=−B −F, 又因为根据式(1)以及ρ和σ的性质, 有[14]:

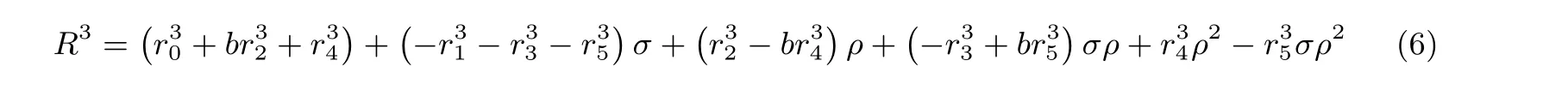
将式(6)代入式(4), 整理可得:

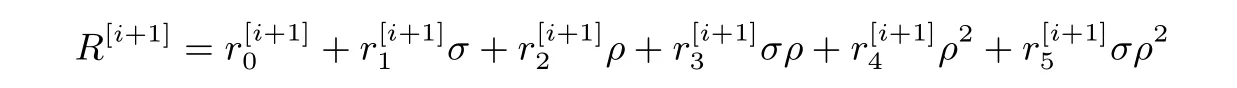
其中:

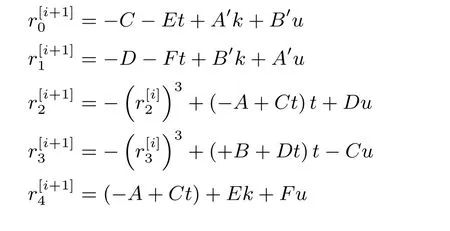
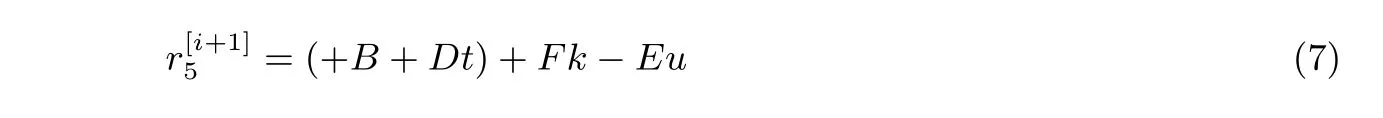
Miller 循环的主要内容就是计算式(7)中的系数. 在式(7)中我们可以发现多个重复出现的因子, 在计算时可以充分利用减少运算量和数据传输.

进行硬件数据通路设计时, 考虑到上述计算方案中乘法运算之间存在一些数据依赖关系, 最多可以有6 个GF(3m) 乘法同时运算, 所以将18 次乘法运算分成三组, 每组用6 个模乘器并行进行计算. 经过调度优化, 式(5)和式(7)的计算过程可以分解为3 个“相位”, 完成6 次乘法, 如表1所示.

表1 Miller 循环的乘法调度Table 1 Multiplication scheduling of Miller’s loop

表1 的调度方案, 包括计算参数k和u的两次乘法在内, 一次Miller 循环需要18 次GF(3m) 乘法、23 次GF(3m) 加法以及10 次GF(3m) 的立方. 相对于Beuchat 等人[15]的方案——14 次GF(3m) 的乘法、58 次GF(3m) 的加法和10 次GF(3m) 的立方, 本文方案虽然增加了4 次乘法, 但把加法次数减少了一半以上.

从上述的调度可以看出, 在每一轮模乘运算中, 第2–5 个MSE 模乘器都有一个相同的操作数, 因此在硬件实现的时候, 这4 个模乘器可以共享一个移位寄存器单元, 从而减少了寄存器的使用. 同时, 这4个模乘器每一个相位的另一个操作数保持不变——除了相位3 中有2 个操作数需要被替换, 这样也大大减少了寄存器的刷新次数和存储器的读写, 可以降低寄存器翻转引起的功耗. 根据以上方案, 我们就可以对Miller 算法进行硬件实现.

4.3.2 Miller 算法单元

所设计的Miller 算法数据通路电路结构如图3 所示. 由坐标更新单元、模乘器阵列和参数计算单元三部分组成, 在控制器的控制下迭代运算. 每轮迭代的中间结果由两个寄存器堆(RF1 和RF2) 保存, 寄存器堆的输出反馈给模乘阵列用于迭代. 采用两个寄存器堆可以提高数据读写的并行度.

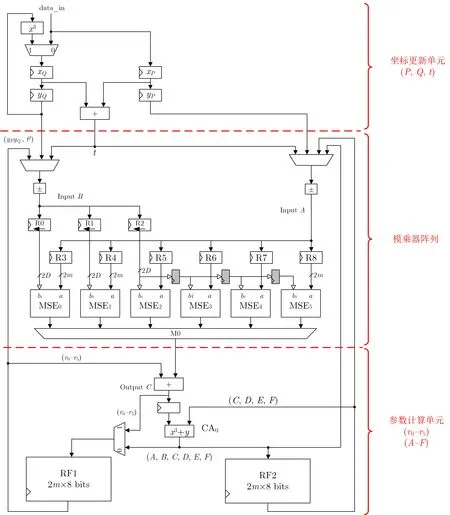
图3 Miller 算法硬件的数据通路结构(µ=1, b=1)Figure 3 Datapath structure of Miller’s algorithm (µ=1 and b=1)

坐标更新单元是eta 对数据的输入与更新模块, 点P(xP,yP) 和Q(xQ,yQ) 的坐标从data_in 端口依次输入, 分别存在4 个相应的寄存器中. 根据eta 对的算法,Q坐标在初始化以及每一轮Miller 循环中都需要进行立方运算, 所以坐标更新单元中用一个立方运算电路实时计算x3Q和y3Q, 加法器用于计算t=xQ+yQ, 并将操作数yP, yQ, t输出给MSE 模乘器, 用于Miller 循环中的模乘运算.

第二部分是6 个模乘器组成的模乘器阵列, 完成GF(36m)稀疏乘法, 是整个设计的主要部分. 其中的6 个MSE 模乘器在每个相位所执行的运算如表1 所示. 其中u,k和t是多个乘法的输入数据, 使用R0, R1 和R2 三个移位寄存器存储, 因为操作数相同, MSE2–MSE5共享R2 输入寄存器, 这减少了3 个2m比特寄存器. 由于存储器的读写带宽存在限制, 每一相位的并发模乘运算的输入和输出必须分时进行,每一轮的6 次模乘运算不是同时开始而是从左到右依次开始的, 在操作数载入以及结果输出时以类似于流水线的方式运行. 相应地, 在MSE3–MSE5的输入端路径上插入了3 级2D比特的延迟寄存器, 把同一个操作数从左到右依次传递给3 个模乘器, 减少了存储器的访问. 模乘运算的结果经过多路选择器分时输出.

参数计算单元计算r0–r5与中间项A–F. 首先RF1 和加法器构成了一个累加结构, 对模乘运算的结果做累加, 用于计算r0–r5(式(7)). 其次, 在一轮运算完成后, 也就是r0–r5依次计算完成时, 继续进行立方累加(由其中的立方-加法单元(图中用x3+y表示) 完成), 得到中间项A–F并且在把结果存入RF2中的同时直接旁路给模乘器进行下一轮的Miller 循环运算.

上述调度方案允许实时计算和更新操作数, 节省了等待数据和访问存储器的时间.

表2 Miller 算法硬件调度表Table 2 Computation procedure of the i-th iteration in Miller’s algorithm

4.4 GF(36m)幂运算电路

算法1 中最终的GF(36m)幂运算采用了论文[20]中的算法, 其电路结构如图4 所示. 由于算法是一系列的串行运算, 包括GF(3m) 上的立方、加法和乘法, 因此, 为了减小面积, 硬件结构中只配置了一个GF(3m) 上的模乘器和一个立方-加法单元执行运算. 另有一个双端口RAM 作为数据存储器. 最终幂运算也是通过微指令进行控制. 幂运算步骤较多且是串行计算, 所以将幂运算的指令固化到ROM 中, 通过计数器产生相应指令的地址.

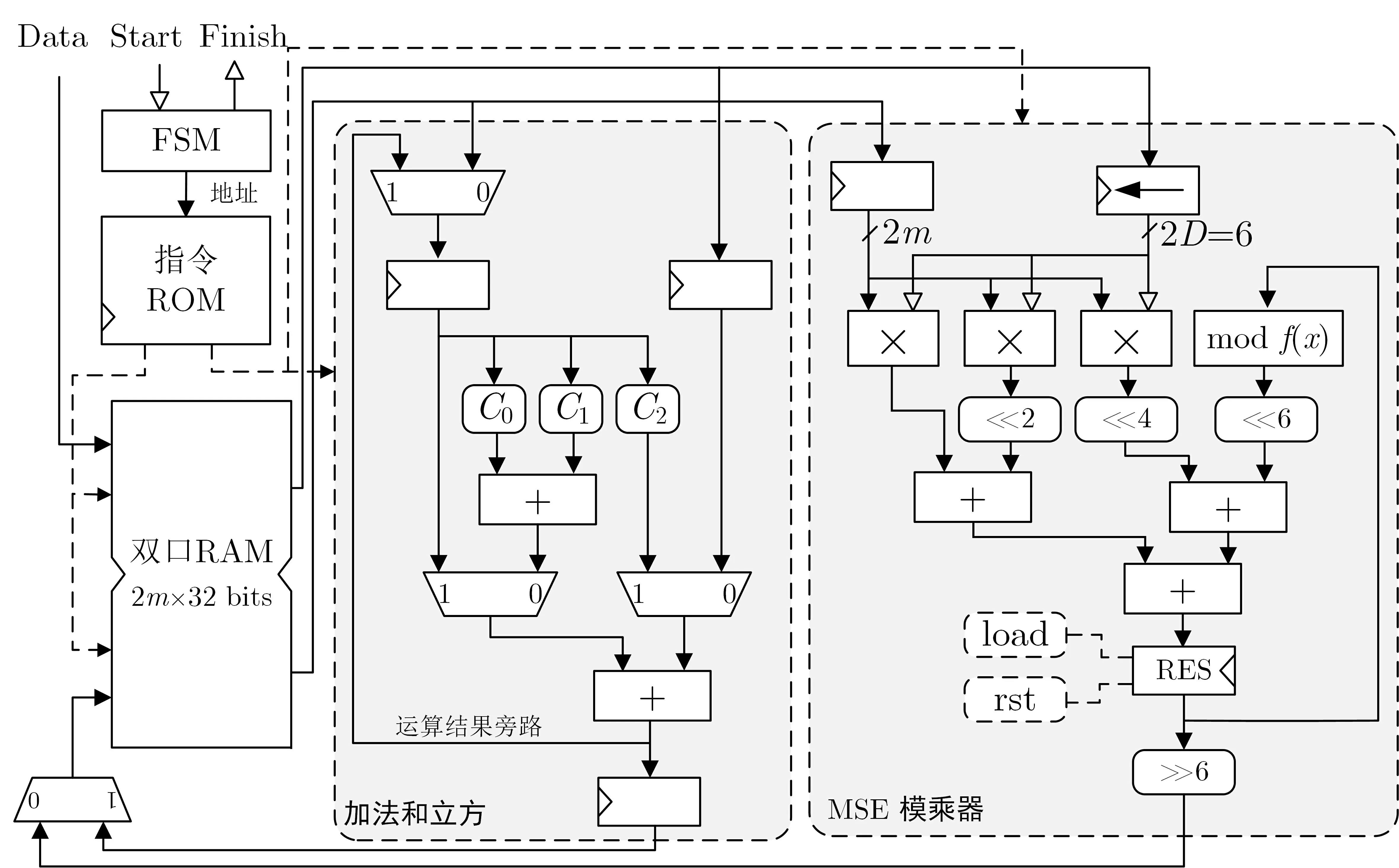
图4 最终幂运算单元电路结构Figure 4 Structure of final exponentiation unit

4.5 eta 对硬件加速器整体结构

在上述Miller 算法单元和最终幂运算单元的基础上实现的eta 对硬件加速器整体结构如图5 所示.Miller 算法单元和最终幂运算单元各自有分立的控制器, 二者之间存在一个交互信号, 当Miller 算法结束,就会触发幂运算开始工作, 二者以流水线的方式工作.

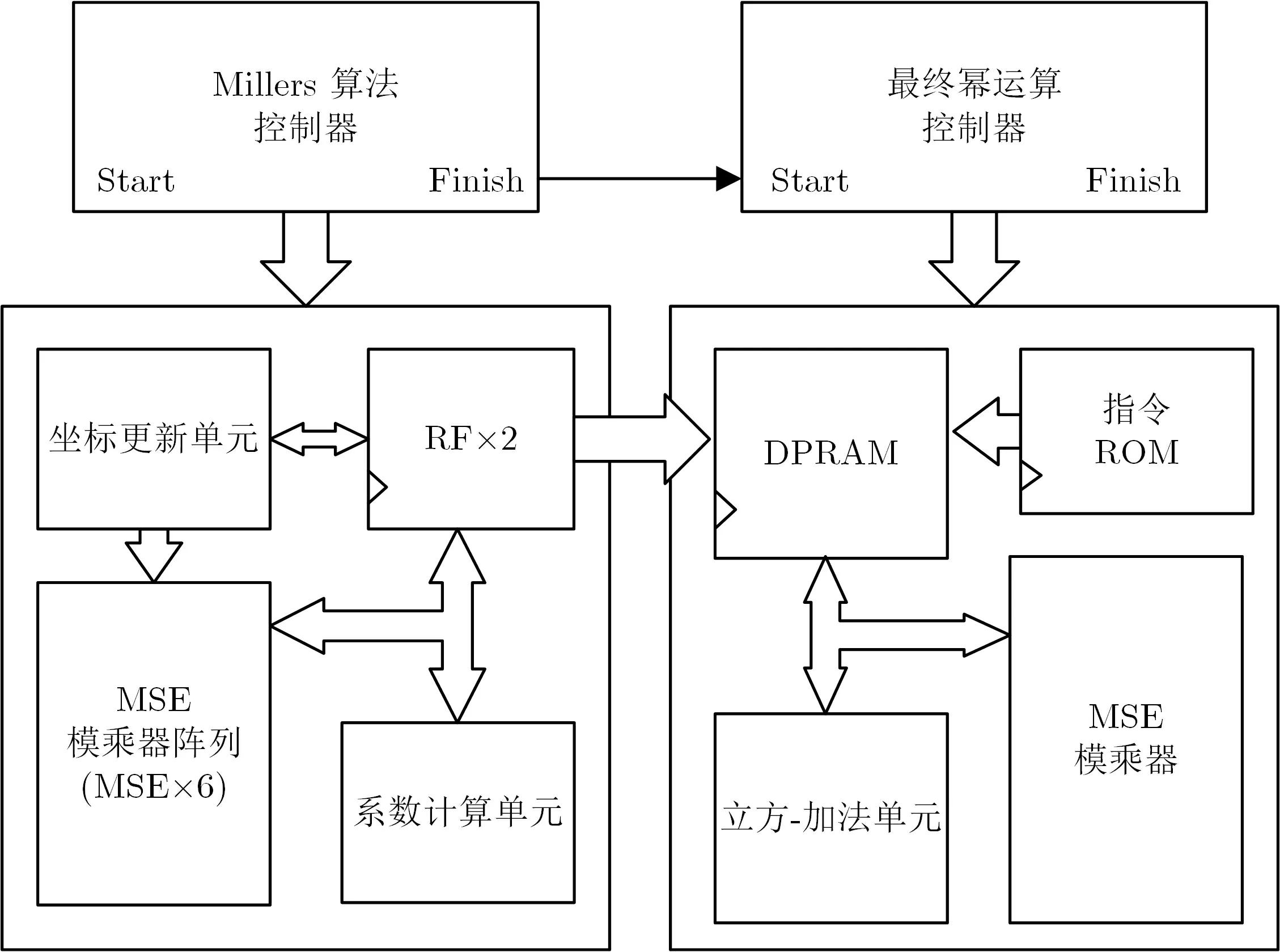
图5 eta 对硬件加速器整体结构Figure 5 Top-level structure of proposed eta pairing accelerator

5 性能评估

我们以上述结构实现了m= 97,D= 3 的三进制eta 对加速器, 能够为IBE 提供相当于66 比特的AES 的安全性. 为了简化模运算与立方运算, 选取了f(x) =x97+x12−1 做为运算中的不可约三项式.在该参数下, Miller 运算和最终幂运算分别需要4851 和3272 个周期. 使用Synopsys Design Compiler(DC), 和Synopsys IC Compiler (ICC) 完成了设计的综合和版图, 工艺为SMIC 90 nm 工艺. 所得的设计版图如图6 所示, 面积为650×650 µm2. 表3 列出了基于布局布线后时序分析和功耗仿真得到的设计参数对比情况, 所有对比设计都是GF(397)的eta 对ASIC 设计. 从表中数据可以发现: 相比于Chung等人的全流水ASIC 设计[10], 本文设计尽管运算时间较长, 但是面积时间积降低了38.8%. 因此硬件实现效率更高, 且电路的功耗也低于对比设计, 更适合用于IoT 设备.

图6 eta 对硬件加速器版图Figure 6 Layout of proposed eta pairing accelerator

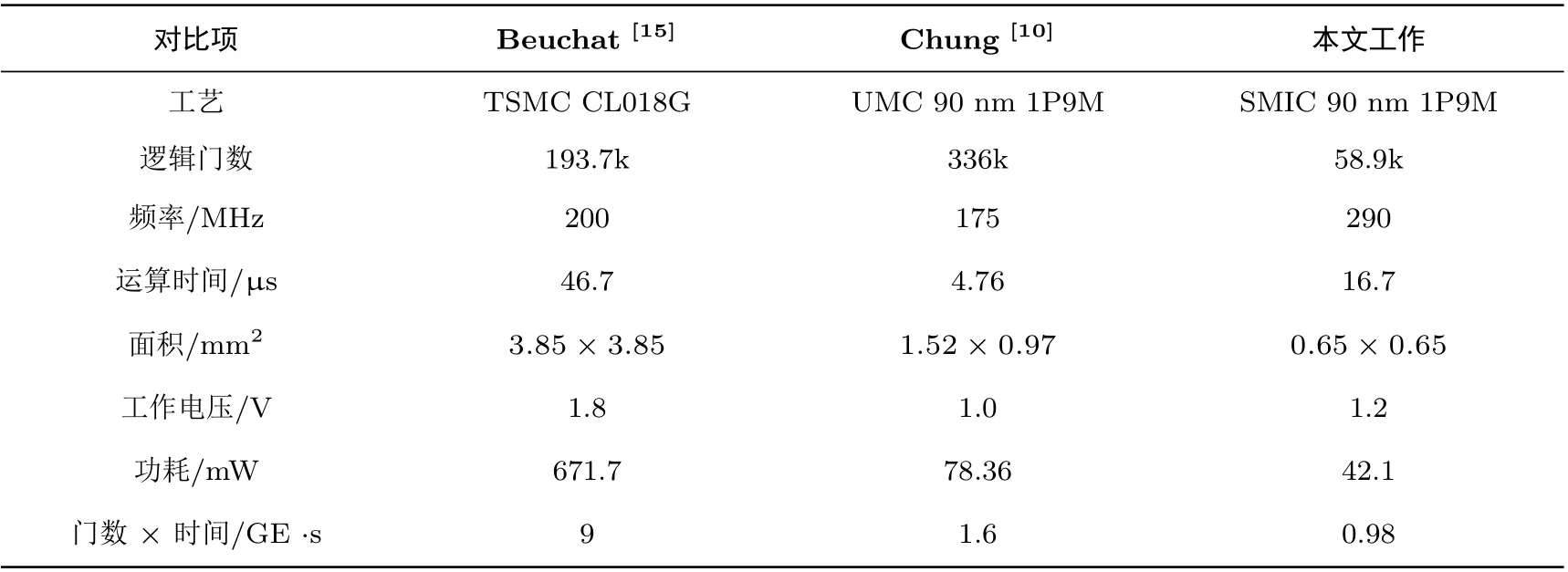
表3 GF(397) eta 对硬件加速器ASIC 性能对比示例Table 3 Performance comparison of GF(397) eta pairing accelerators

6 结论

本文设计了一个低开销的三进制eta 对硬件加速器. 对Miller 循环中的运算进行整合后, 提取公共项、优化调度、平衡乘法和加法运算的数量、充分共享中间结果, 以减少数据传输、暂存和存储器访问的数量. 顶层设计将Miller 算法和最终幂运算以流水线方式运行, 提高了整体的硬件效率, 实现了一个更加高效的双线性对硬件加速器. 版图后仿真结果表明, 该设计比现有相同功能的ASIC 的面积延时积减小了38.8%. 它更加适合物联网等轻量级应用场景. 此外, 虽然由于SM9 算法基于的是素数域椭圆曲线和扩域上椭圆曲线上的双线性对, 支持的双线性对类型限于Weil 对、Tate 对、Ate 对、R-ate 对4 种[2], 本文设计无法直接用于SM9 算法的实现, 但是Miller 算法的核心运算——切线函数的模幂-乘, 是一致的, 本文的设计思想——将模幂-乘运算进行整合优化对于其它对的Miller 算法的优化仍具有借鉴意义, 我们未来将探索SM9 算法的低高面积效率硬件设计.