电子投票协议下的基于格的可链接门限环签名*
庄立爽, 陈 杰,2, 王启宇
1. 西安电子科技大学ISN 国家重点实验室, 西安 710071
2. 西安电子科技大学 西电密码研究中心, 西安 710071
1 引言
在信息安全技术和计算机网络技术的支撑下, 传统的投票方式已经难以满足人们的需求, 而日益兴起的电子投票逐渐成为各种政治、娱乐活动中用于民意统计的主要方法, 它以其高效、便捷的特性而为人们所普遍接受. 一般来说, 安全的电子投票必须满足以下八个特性: 合法性、匿名性、公正性、完备性、可验证性、正当性、唯一性和无争议性. 当今的电子投票大多数都是建立在密码学基础上的, 大致可以分为以下几种类型: 混合网模型[1]、盲签名模型[2]以及同态加密模型.
Fujioka 等人采用比特承诺和盲签名技术, 实现了第一个实用的适合于大群体的电子投票方案(FOO)[2], 协议较混合网模型一类效率提升很大, 但该方案存在选票碰撞、选票可能无法打卡以及管理中心可以冒充投票者进行投票等问题. 此后出现大量基于群签名、盲签名的电子投票方案[3–5]. 文献[3]提出一种基于RSA 密码体制的电子投票协议, 该方案不允许投票者中途弃权, 难以满足实际要求. 2003年, 陈晓峰等利用群签名协议和时限承诺协议设计了一个电子投票方案[4], 虽然解决了选票碰撞问题, 但只有在注册机构或计票机构诚信公正的前提下才能保证投票者身份的匿名性, 否则将会通过选票追踪到投票人的所有信息. 2013 年, Ghavamipoor 等设计了一个匿名电子投票协议[5], 该协议利用投票者无需生成公私钥对的方法提高了协议效率, 但投票阶段必须依赖于一个不可追踪的安全电子邮件系统向认证机构发送选票, 妨碍了其实际应用. 从对目前国内外研究的整体分析来看, 如何保证电子投票中的匿名性、不可重用性、公开可验证性和防止管理中心冒充投票人选票这些问题是学者们一直以来在电子投票安全性上的重点研究方向.
抗量子的电子投票系统直到2016 年才首次提出, Chillotti 提出的基于LWE 算法的电子投票系统[6],该方案基于格密码, 大大简化了正确性、隐私性和可验证性的证明. 该方案是基于LWE 的电子投票协议的第一个实例, 也是第一个真正意义上的、具有完整的系统架构和较完备密码学性质的抗量子电子投票系统. 但该方案面临无法对选票合法性进行验证、效率低等问题, 实践性不强. 2017 年, 文献[7] 提出的基于混合网的电子投票系统, 该方案虽然在基于混合网模型的电子投票类型中实现了公开验证和效率上的提升, 满足电子投票的基本安全特性, 但不能防止二次投票. 2018 年, 文献[8] 提出了一个安全、实用的抗量子电子投票系统, 并给出了详细的证明. 文献[8] 的系统比Chillotti 方案的效率有所提高, 但该方案仅仅是一个完备的电子投票系统, 不能防止二次投票. 如何应对量子计算机的攻击并克服现有方案的不足, 构建一个基于抗量子密码的高效可验证电子投票的系统正是我们研究的主要问题. 2019 年, Naranjo[9]基于困难问题构建的同态加密系统设计了一个抗量子的电子投票系统. 2020 年, 文献[10] 构造了一种基于SEAL 库的同态加权电子投票系统, 该同态加密系统的安全性格上RLWE 困难问题, 该系统可以满足多个候选人投票、加权投票和高效计票的应用需求.
为解决以上问题, 本方案基于格密码为环签名增加抗量子性, 应用消息块共享技术和填充排列技术构造门限环签名以适应一种新的电子投票场景, 以及为环签名增加可链接性质使得签名具有不可重复性. 本文提出一种基于格的可链接门限环签名(LTRS) 方案, 给出了LTRS 方案安全性证明和性能分析, 并将LTRS 应用到电子投票协议中, 该协议满足合法性、匿名性、公正性、完备性、可验证性、正当性、不可重用性、无争议性、坚固性、实用性和抗量子性.
在最后一部分, 我们将本方案与之前的方案分别从安全特性和签名大小两个方面进行了对比. 文献[11] 的算法是由Choi 和Kim 基于LWE 困难问题提出的, 可以抵抗已知攻击且使用了消息块共享的技术, 但此算法效率不高. 文献[12] 是基于SIS 困难问题提出的算法, 能够抵抗已知攻击, 但不具有可链接性. 文献[13] 是基于双线性对的困难性假设提出的一种可链接环签名, 但该方案不具有抗量子性质. 文献[14] 是基于格的困难问题SIVP 提出一种门限环签名, 其优点是由于基于格密码, 其操作步骤较线性更快且具有门限机制, 在环成员为100 个的情况下, 其签名大小达到0.26 Mbytes. 本文提出的LTRS 方案基于理想格, 能够抵抗已知攻击, 且具有可链接性, 当环成员为100 个且门限值为2 时, LTRS 签名大小为0.0351 Mbytes. 在计算开销上, 我们证明了LTRS 方案在参数设置、密钥分配、签名和验证的运行时间是安全参数内多项式可计算的. 在通信开销上, 我们给出了LTRS 方案与其它方案在签名大小上的对比.
2 预备知识和系统模型
2.1 符号定义
R 表示正实数集合. Z 表示整数集合. 对于所有正整数d, [d] :{1,2,··· ,d}. 已知集合S,x ←S表示为:x是均匀随机从集合S中抽取的样本. Zp表示商环Z/pZ.D: ZP[x]/〈xn+1〉,xn+1 是不可约多项式, 其中n是2 的幂,p是素数且p ≡3 mod 8,D中元素的多项式次数为n −1, 系数在{−(p −1)/2,··· ,(p −1)/2}之内. 多项式向量用(a,b,···) 表示(注解:a1,a2,··· ,am ∈D,m是正整数, (a1,a2,··· ,am) 的多项式向量由a表示). 对于一个多项式a, 它的无穷范数l∞:||a||∞=maxi|a(i)|,其中a(i)是a的系数. 相似地,a=(a1,a2,··· ,am) 的最小范数定义为:||α||∞=maxi||ai||∞,i ∈[m].
令n为系统的安全参数, 其他参数由n隐式确定. ploy(n) :f(n) =O(nc)(f(n) 是可忽略的当且仅当f(n)
2.2 格
定义1(格) 格是Rm一类具有周期性结构离散点的集合. 格是m维欧式空间Rm的n(m ≥n) 个线性无关向量组b1,b2,··· ,bn的所有整系数线性组合, 即
一般情况下,λ1(L(B)) 表示格L(B) 中最短向量.
定义2(SIVPγ问题) 给定一个n维格L,SIVPγ找到n个线性独立格向量,其长度最大为γ·λn(L).以上, 关于格的计算复杂性问题请读者参考文献[15].
2.3 抗碰撞哈希函数
定义3对于整数m和D×⊆D,H(D,D×,m) ={ha:a ∈Dm}, 对于任意z ∈Dm×, 等式ha(z)=az=∑aizi成立, 其中a=(a1,a2,··· ,am) 且z=(z1,z2,··· ,zm),aizi的内积在D中计算.
对于任意y,z ∈Dm,c ∈D,H(D,D×,m) 内的哈希函数满足式(2)和式(3)两个条件.

2.4 统计距离
统计距离即两个概率分布的区分.
定义5(统计距离) 令X和X′是一个集合S的不同变量,X和X′的统计距离如式(4)定义.
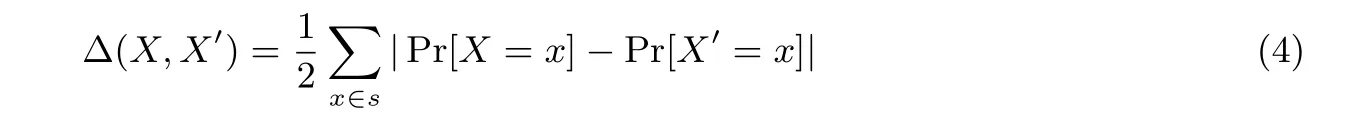
假设1 表明, 统计距离不会随着变量增加而增长.
假设1[16]令X和X′是一个集合S的不同变量, 对于∀f ∈S,f(X) 和f(X′) 的统计距离至多为∆(f(X),f(X′))≤∆(X,X′).
即, 如果两个随机变量(Xλ) 和(Xλ′) 是可忽略的, 攻击者在区分带样本的(Xλ) 和(Xλ′) 上只有一个可忽略的优势, 在假设1 中, 没有假设函数f的计算复杂性, 所以不管攻击者是有界还是无界的, 它都成立.
但当考虑多个变量时, 统计距离可能会增加. 可由统计距离的定义得到一个结论, 如果X,Y来自分布φ,X′,Y′来自分布φ′, 可以得到不等式(5).
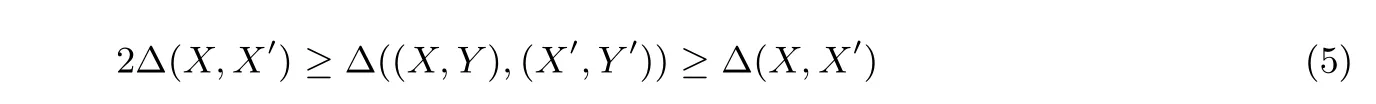
一个拥有同一分布的多个样本的攻击者可能比起只拥有一个样本的攻击者更容易区分, 因此, 如果两个随机变量的统计距离有上界ε(k), 已知同一分布的s个变量, 攻击者盲目猜想的上界是s·ε(k).
以上, 更多关于统计距离的细节请参考文献[16].
2.5 消息块共享

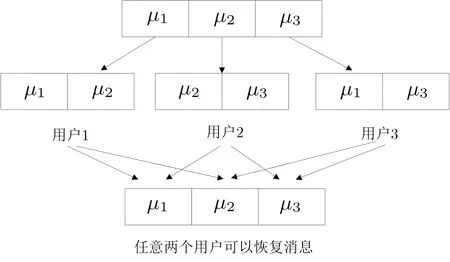
图1 消息块共享Figure 1 Message block sharing

2.6 填充排列技术
Choi 等人[11]使用一个参数提取算法——门限参数提取算法, 把消息及其长度作为输入, 输出(λ,N,t),λ是安全参数,N是环的大小,t是生成有效签名的成员数门限值. 这种方法在签名方案的实际应用时存在严重的缺陷. 首先, 门限参数提取算法要求消息至少有d位, 因此如果消息很短, 门限签名就不能工作. 其次, 要签名的消息的位长决定了门限值t和N的大小, 由于生成消息的门限签名之前, 门限值总是与系统参数一起设置的, 因此这在实践中不可行. 为了避免这些缺点, 本文使用了称为填充排列的消息预处理技术, 使门限签名更实用.

2.7 模型
2.7.1 系统模型
石怡等人[17]曾提出一个投票问题: 一个公司包含两类董事, 一类任职董事(8 人), 另一类不在公司任职(12 人); 要通过一个提案时, 需半数以上董事同意外, 为保证可操作性, 还要求其至少包括6 名任职董事, 同时保证表决的匿名性.
本文提出的方案的系统模型如图2 所示, 在这种类型的方案中, 存在多个地位相同的管理中心, 注册工作由管理中心完成, 选票的认证及计票工作由计票中心完成. 通常来说, 电子投票协议一般包括: 投票人V, 投票管理中心A, 计票机构C.
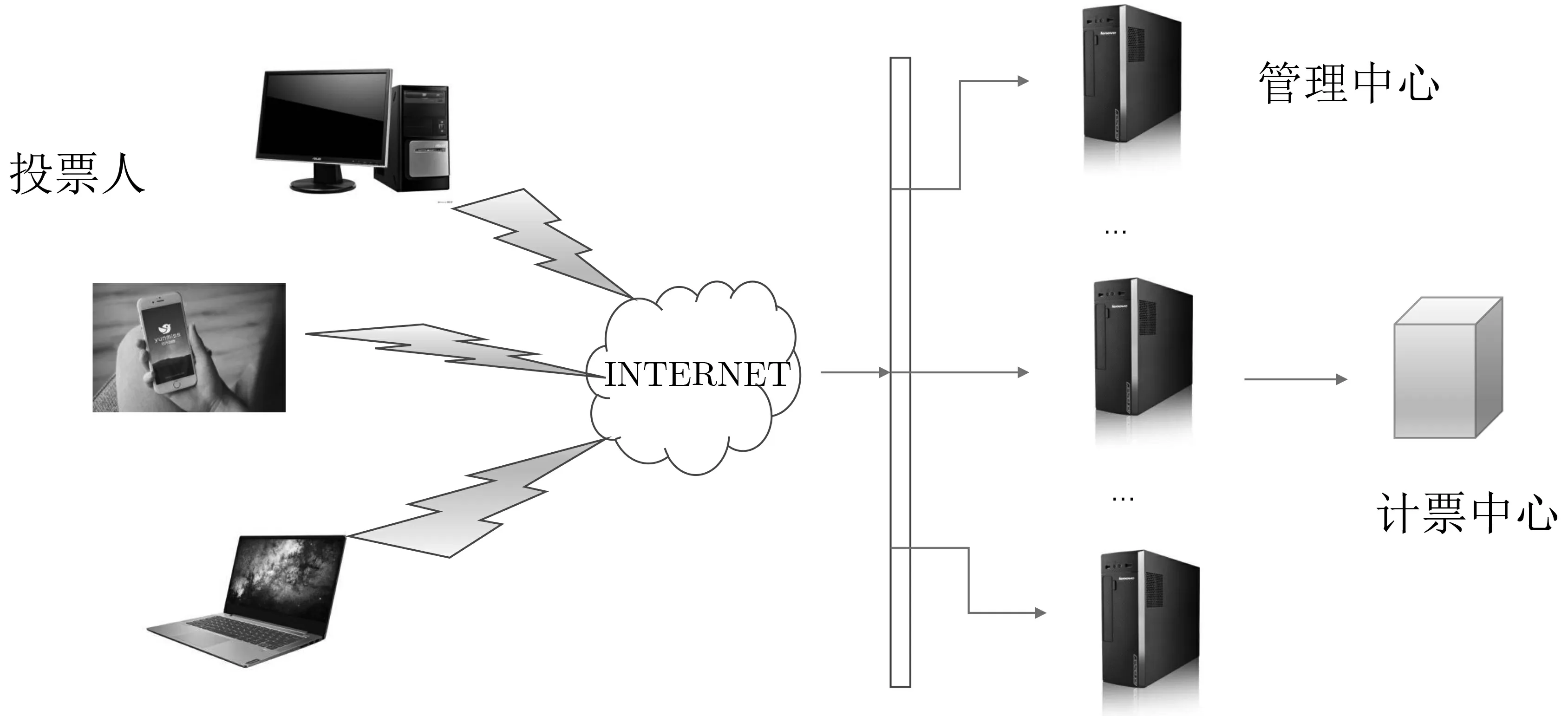
图2 电子投票系统模型Figure 2 E-voting system model
2.7.2 形式化定义
可链接门限环签名方案由以下五个多项式时间内的算法组成:
初始化: 输入安全参数, 输出公共参数和门限参数(λ,N,t).
密钥提取: 为每位用户i ∈U生成公私钥对(pki,ski).
签名算法(µ,U,S): 此算法是一个交互式协议, 将U内t个用户的一组公钥,S内t个用户一组私钥和消息µ作为输入, 输出µ的t/N的门限环签名σ.
签名验证算法(µ,σ,t,U): 此算法是一个确定性算法, 输出accept 或者reject.
可链接验证算法: 输入σ和σ′, 输出Link 或者Unlink.
3 可链接门限环签名
本文提出一种基于格的可链接门限环签名(LTRS), 并将此签名应用到电子投票协议中, 该方案引入了可链接的环签名, LTRS 协议交互由管理中心、用户和验证者共同完成, 交互流程图如图3 所示, 该算法由初始化、密钥提取、消息生成、签名、签名验证和可链接验证一共6 个步骤组成.

图3 LTRS 交互流程图Figure 3 LTRS’s interactive diagram
3.1 形式描述
步骤1: 初始化
管理中心给定安全参数λ,N和t, 输出公共参数P1={λ,t,N,d,n,m,p,C,H0,H,H′}.
输入:λ,N和t.

(4) 令C ←D,C ̸=0.
(5)H0={0,1}∗→Ds,c是一个公共的抗碰撞哈希函数, 将用于验证消息的完整性.
(6)H′={0,1}∗→Ds,c,H={0,1}∗→Ds,c是两个抗碰撞哈希函数, 在安全性证明中模拟随机预言机.
输出:P1={λ,t,N,d,n,m,p,C,H0,H,H′}.
步骤2: 密钥提取
管理中心为用户Ui生成公私钥对(pki,ski)=(hi,si).
输入:P1.
(1) 令si=(si,1,si,2,··· ,si,m)←Dms,c.
(2) 如果si,j中没有一个是可逆的, 返回步骤(1).
(3) 令j0∈{1,2,··· ,m}使得si,j0是可逆的.
(4) (ai,1,ai,2,··· ,ai,j−1,ai,j+1,··· ,ai,m)←Dm−1.
(5) 令ai,j0=s−1i,j0(C −∑j̸=j0ai,jsi,j) 且(ai=ai,1,ai,2,··· ,ai,m).
(6) 输出(pki,ski)=(hi,si),h是由ai定义的哈希函数族H中的哈希函数.
步骤3: 消息生成
给定消息µ, 管理中心进行填充排列操作, 最后把µ分成d个消息区块{µ1,µ2,··· ,µd}.
输入:P1,µ.

(2) 对µ进行填充操作, 将µ用0 bits 从g填充至ω·d, 表示为ˆµ.
(3) 从ω·dbits 置换集合中随机选取一个置换π.
(4) 计算并且将π(ˆµ) 分为d个消息区块{µ1,µ2,··· ,µd}.
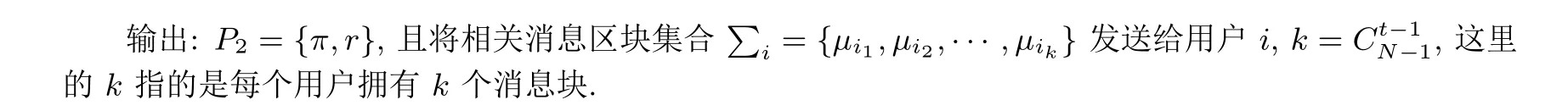
注意: 用户要保证消息区块保密.
步骤4: 签名
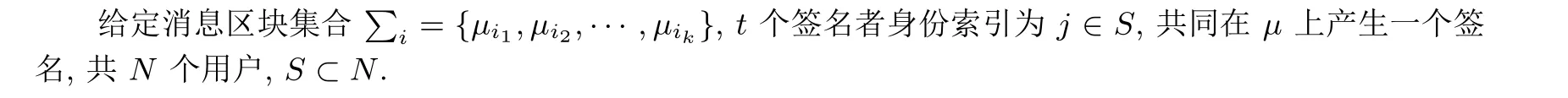
输入:P1,P2, ski,µ.

(4) 一旦收到Ω, 每个签名者确保它的hj(yj) 是在h1(y1),h2(y2),··· ,hN(yN) 之内的, 并且检查Ω和y∗的正确性. 然后, 它令µ[j]=µj1||µj2||···||µjk, 再计算关联标签j=H(Ω,µ[j],y∗,r)(可得j在Ds,c内),zj=sjj+yj.
(5) 如果zj/∈Dmz, 返回步骤(2).
输出:σ={z∗,e∗,y∗}.
步骤5: 签名验证

输出: 如果所有条件都满足, 验证者输出1, 否则输出0.
步骤6: 可链接性验证

4 安全性分析
本节将从LTRS 签名正确性、不可区分源匿名性和一定概率的不可伪造性来对LTRS 签名的安全性进行证明.
定理1LTRS 方案是正确的.
证明:假定σ={z∗,e∗,y∗}是对µ的签名, 消息块共享技术使得消息经处理后来自环中至少t个签名者, 否则的话消息不能被完整组合而成. 所以一个合法签名必须满足步骤5 的(1). 由于步骤4 的(2)–(5) 保证了签名只包含Dmz中的元素, 那么步骤5 的(2) 也是成立的. 关于步骤5 的(3):
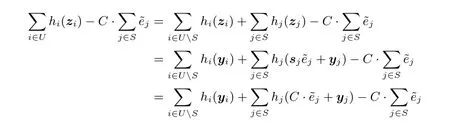
由于

因此对于一个有效签名来说, 步骤5 的(3) 成立.
定理2假设Melchor 等人的环签名步骤[18]是匿名的, LTRS 在具有统计上不可区分源匿名性.
证明:在不可区分的源匿名游戏中, 敌手可依赖一个随机比特b和系统公共参数P1获得一个签名,两个不同的私钥集合sk0={ski1,0,ski2,0,··· ,skit,0},sk1={ski1,1,ski1,1,··· ,skit,1}, 和消息µ. 除了{ski1,0,ski2,0,··· ,skit,0}和随机比特b, 其余参数对敌手已知. 令Xb,P,skbµ是随机变量, 代表敌手通过一系列已知参数获得的签名. 相似于Melchor 签名[18]的匿名性证明, 可以将本方案的skb与其环签名方案的skib对照来看. 本方案和Melchor 方案[18]的不同之处在于: 在Melchor 方案中, 本方案中的ˆz是由ˆzi ←ˆsi·ei+ ˆyi生成的分量, 其中ˆsi是私钥, ˆyi是从Dmy中随机选择的,ei是通过哈希函数H计算的, 其他元素是从Dmz中随机选择的. 但是在本方案中,z∗有t个部分是由ˆzi ←ˆsi·ei+ ˆyi产生的, ˆyi是从Dmy中随机选择的,ei是通过哈希函数H计算的, 其他N −t个元素是从Dmz中随机选择的.
在Lyubashevsky 方案[19]中的定理6.5 阐述, 对于任意由哈希函数族H选择的h, 消息µ, 和任意两个私钥ˆs,ˆs′∈Dms, 使得对于随机变量ˆz(ˆz′) 和e(e′)(其中e(e′) 分别是签名算法的输出结果),h(ˆs)=h(ˆs′), ∆((ˆz,e),(ˆz′,e′))=n−ω(1)成立. 令Xb,P,skib,µ,R是描述Ring-sign(P,skib,µ,R) 输出结果的随机变量.P1={λ,t,N,d,n,m,p,C,H0,H,H′},P2={π,r},skib,µ和R是算法的输入. 在Melchor的方案中, 如果这些变量的域都不是则failed, 当b ∈{0,1},∆(X0,P,ski0,µ,R,X1,P,ski1,µ,R) =n−ω(1). 在本方案中, 迭代此结果t −1 次, 可得出结论∆(X0,P,ski0,µ,R,X1,P,ski1,µ,R)=n−ω(1).
定理3假定存在一个多项式时间的伪造者F, 至多可进行t −1 次破坏性询问, 可以对提出的可链接门限环签名以概率ε输出一个有效伪造结果. 通过利用F, 可构造一个算法B以至少(N −t+1)tε/N2的概率输出一个伪造结果.
证明:假定存在伪造者F, 可以对提出的可链接门限环签名以不可忽略的概率ε输出一个有效伪造结果. 通过应用F, 构造一个多项式时间算法B, 算法B为Lyubashevsky 方案以不可忽略的优势输出伪造结果[20].
B收到作为输入的一个公钥pk∗,B应用带有输入公钥pk={pk1,pk2,··· ,pkN}的F.B选择一个指引i∗←{1,2,··· ,N}和集合pki∗=pk∗. 其他公钥由密钥生成算法生成.B模拟F的预言查询如下:
(1) 当F对消息µ作签名询问,B通过运行签名算法生成响应, 其中有t个签名者, 其身份指引i ̸=i∗.

(4)B诚实地回答F为用户i ̸=i∗提交的任何破坏性询问, 若F对i∗作一个破坏性询问,B简单地中止. 那么F完全可以作t −1 次破坏性询问.

定理4LTRS 方案是可链接的.
证明:根据定理3 可知非环成员是不能够伪造合法的环签名的. 我们只需要考虑敌手F伪造与其它环成员签名链接的签名. 假定敌手F能够成功, 即σ={z∗,e∗,y∗}是合法伪造. 根据定义, 我们知道tag ==H(Ω,µ[j],y∗,r), 且知道SIVPγ问题是困难的, 且定理3 已被证明. 又因为可链接标志是j=H(Ω,µ[j],y∗,r), 每个签名者的tag 都是不同的, 当两个签名具有相同的tag 时, 那么这两个签名就是由同一个签名者所签.
5 性能分析
5.1 安全特性对比
在这一节, 我们将LTRS 方案与文献[11–14] 四个方案在安全特性上进行对比. 由表1可知, 五个方案都可抵抗已知攻击, 在可链接性质上, 只有文献[13] 和LTRS 方案具备可链接性质, 但文献[13] 是基于双线性对的困难问题构造的可链接环签名, 不可抵抗量子攻击. 在门限性上, 文献[14] 的方案和LTRS 都具备门限性质, 但文献[14] 不具备可连接性.
由表1 可知, LTRS 既具备可链接性质和门限性, 也具备抗量子特性. 以上三个性质为签名应用的场景提供了更多可能.

表1 安全特性对比Table 1 Comparison of security features
5.2 计算开销

定理5参数设置、密钥分配、签名和验证的运行时间是安全参数内多项式可计算的.
证明:显然, 参数设置和验证算法是在多项式时间内执行的, 只需考虑密钥分配和签名两个算法的迭代.
定理3 显示, 步骤2 中的(1) 中选择的每个多项式都是可逆的概率以指数形式接近于1, 因此预期的迭代大约是1. 所以密钥分配算法的运行时间是多项式时间的.

以上, 本方案的计算开销很小. 步骤1 的计算开销主要包括一些参数的采样和哈希函数的选择. 步骤2 中只需要一个向量的选择以及向量内积. 步骤3 的计算包括比特值填充和一个随机置换. 步骤4 的计算主要包括两个哈希函数计算、几个向量的采样和计算. 步骤5 也包含几个哈希函数和向量的运算. 步骤6只需要一个向量的选择以及向量内积. LTRS 签名的参数设置、密钥分配、签名和验证的运行时间是安全参数内多项式可计算的.
5.3 通信开销
表2 和表3 给出了本文提出的LTRS 方案与其它方案在签名大小上的对比. 其中包含王启宇等人提出的BVLRS 方案[13], Cayrel 等人提出的CLRS 方案和T-CLRS 方案[21], 与Bettaieb 等人提出的改进的基于格的门限环签名方案[14].
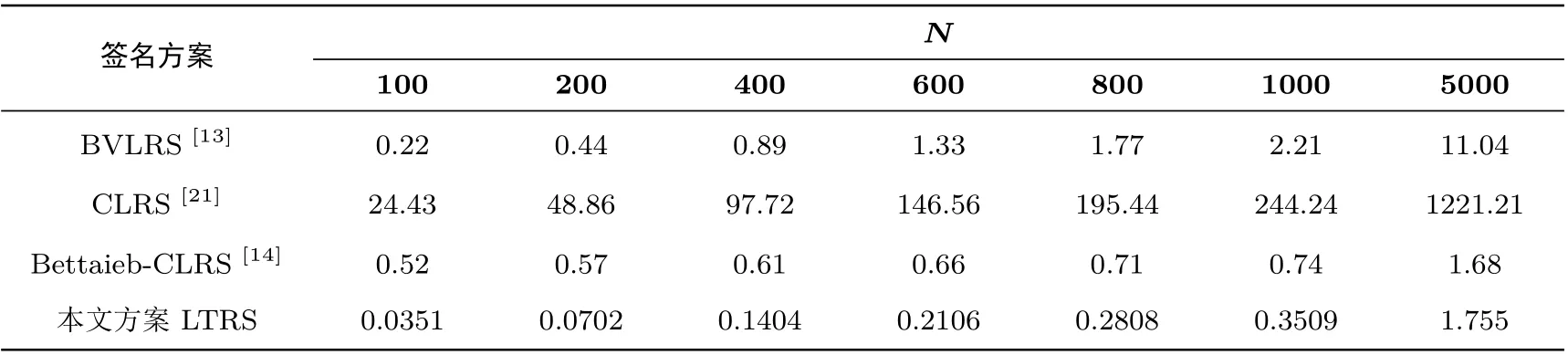
表3 t = 2 时签名大小对比(Mbytes)Table 3 Comparison of signature’s size with t = 2 (Mbytes)
相较于BVLRS 方案, LTRS 方案具有抗量子性和门限性以及签名长度较短的优势. 相较于T-CLRS方案, 在N相同的情况下, LTRS 方案的签名大小相对较短, 除此之外, 由表2也可看出, 同T-CLRS 方案类似的是,t大小的改变对LTRS 方案的签名大小几乎不产生影响.

表2 N = 100 时签名大小对比(Mbytes)Table 2 Comparison of signature’s size with N = 100 (Mbytes)
令参数设置为n=64,m=2048,q=257, 承诺长度224 比特将提供111 的安全级别. LTRS 方案的构造中, 签名由两个部分组成, 第一部分的每个元素属于Dmz, 第二部分的每个元素属于Ds,c(具体参考步骤5(1)).
各方案签名大小对比:

由表2 和3 可知, LTRS 方案的签名大小是随着t和N的大小的改变而改变的, 通过和Bettaieb-CLRS[14]的工作对比, 在N相同的情况下, 我们的签名大小相对较小. 然而随着t的增加, LTRS 方案的签名大小并不会发生明显变化. 除此之外, 本方案还同BVLRS 方案[13]进行了签名大小的对比. BVLRS方案是基于双线性对的可链接环签名, LTRS 是基于格的可链接环签名, 相较于BVLRS 方案, LTRS 方案虽然在计算上的步骤相对复杂一些, 但LTRS 方案是具有抗量子性质的, 并且如表3 所示, LTRS 方案在签名长度上也相对BVLRS 方案较短, 通信开销较小.
通过图4 和5 也可直观看出本方案与其它方案在签名长度上的对比.
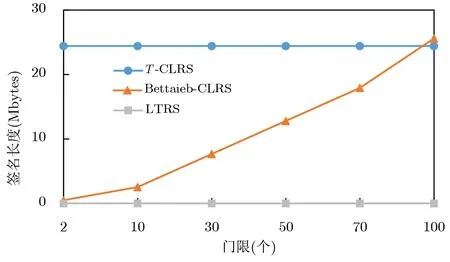
图4 与T-CLRS [21] 和Bettaieb-CLRS [14] 签名长度对比图Figure 4 Comparison of signature’s size with T-CLRS [21] and Bettaieb-CLRS [14]
由图4 可知, 当环成员的个数固定时, 门限值的改变并不会对签名长度大小产生很大影响, 且在门限值相同的条件下, LTRS 方案相对于文献[14] 的算法的签名长度较短. 由图5 可知, 当门限值一定时, 签名长度会随着环成员的增加而增大, 但较文献[14] 相比签名长度较短; 当环成员数基数较大时, LTRS 签名长度的增长速率较BVLRS 签名较小, 也就是说, 在大规模成员的签名场景下, LTRS 签名的实用性更强, 效率更高.

图5 与BVLRS [13] 和Bettaieb-CLRS [14] 签名长度对比图Figure 5 Comparison of signature’s size with BVLRS [13] and Bettaieb-CLRS [14]
6 电子投票协议
LTRS 交互流程是由管理中心A初始化整个系统, 生成公私钥和公共参数, 投票时, 投票人通过比特承诺技术来隐匿自己的选择, 将自己所属的类别信息嵌入到选票中, 随后发送选票给n个管理中心申请签名, 签名采用LTRS 方案. 管理中心检验投票人的身份和类别信息, 为合法投票人的选票进行签名, 并将投票人所属类别标识嵌入到签名信息中, 用来区分不同的类别, 最后将签名返还给投票人, 投票人计算出最后的有效签名. 最后, 计票中心验证签名并进行计票. 整个投票过程中的数据均可公开公布, 根据这些数据, 任何人都可以验证投票结果是否正确. 交互流程图如图6 所示, 共由以下6 个步骤组成.
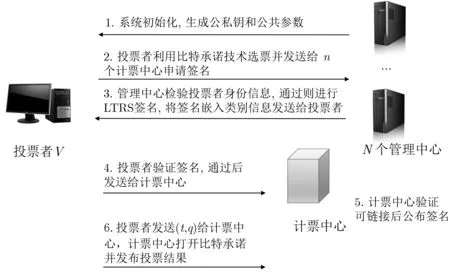
图6 电子投票协议交互图Figure 6 E-voting protocol’s interactive diagram
协议的具体步骤如下:
(1) 本方案参与人员及其担任角色:
投票人v: 其身份为ID.
管理中心A:{A1,A2,··· ,An}, 检验投票人的身份和类别信息, 为合法投票人的选票进行签名.
计票中心: 负责收票, 计算最终的投票结果.

(2) 管理机构运行初始化算法, 系统的公私钥为(pki,ski) = (hi,si), 设Sub1,Sub2,··· ,SubI是I个类别的标识信息.且y∗=H′(h1(y1),h2(y2),··· ,hN(yN),Ω), 然后L将h1(y1),h2(y2),··· ,hN(yN) 和Ω 以及y∗分享给剩下t −1 个签名者. 投票人随机选择q, 对选票v进行比特承诺x=f(v,q). 计算令x[j]=xj1||xj2||···||xjk. (ID,h,Subi,Ω) 发送给每个管理中心Ai.
(4) 每个签证中心Aj检验投票人的身份ID 和他所属类别标识Subi, 若二者都合法则一旦收到Ω,每个签名者确保它的hj(yj) 是在h1(y1),h2(y2),··· ,hN(yN) 之内的, 并且检查Ω 和y∗的正确性. 再计算关联标签j=H(Ω,x[j],y∗,r),zj=sjj+yj. 发送σ={z∗,e∗,y∗}给投票人.

(6) 计票中心收到签名后, 运行可链接验证算法. 若可链接则舍弃签名, 否则接受.
(7) 投票人看到自己的选票被公布出来以后, 发送t,q给计票中心, 计票中心利用q打开比特承诺,计票并公布结果. 利用Subi信息, 计票中心可以很方便地统计每类投票人的投票情况.
7 电子投票协议安全性分析
新的电子投票协议满足合法性、匿名性、公正性、完备性、可验证性、正当性、不可重用性、无争议性、坚固性、实用性和抗量子性.
(1) 完备性: 在协议中, 当诚实管理中心的个数≥t时, 合法的投票人必然能够获得签名. 当他发现自己的选票没有被计票机构公布时, 可以提出抗议. 计票时, 投票人发送解密选票的承诺因子q, 所有能正确解密的选票即为合法的选票, 而所有不能解密的选票则为不合法的选票. 因此所有有效的选票必然会被正确统计, 满足完备性.
(2) 合法性: 签证中心会检验投票人的身份ID 及其所属的类别Subi, 只有合乎条件的人, 才能获得签证中心的签名.
(3) 不可重用(唯一) 性: 计票中心收到签名后, 运行可链接验证算法. 如果是可链接的, 则计票机构认为这是两张相同的选票, 只保留一张, 投票人不可能投出多张选票, 因此方案满足不可重用性.
(4) 匿名性: 投票人将选票进行比特承诺之后, 依据消息共享技术令x[j]=xj1||xj2||···||xjk, 然后对其使用环签名进行加密. 而通过匿名通讯信道发送选票和承诺因子, 也不会暴露投票人的身份.
(5) 公正性: 管理中心对选票内容是不可见的, 只有投票者本人才能够验证选票的内容. 并且只有当计票机构公布了所有合法的选票后, 投票人才投出承诺因子, 解密选票获得选票的真实内容.
(6) 可验证性: 利用公告牌上公布的签名和t、q, 任何人都可以利用管理中心的公钥及参数验证选票的合法性, 同时可以利用承诺因子q检验计票中心解密的正确性.
(7) 正当性: 方案的注册部分可以防止恶意的投票者进行投票.
(8) 无争议性: 由于本方案是基于LTRS 和比特承诺技术, 因此方案的安全性是可证明的, 方案中的各方的公钥都是公开的, 任何投票人或第三方都可验证方案过程的正确性.
(9) 坚固性: 本方案采用了门限签名方案, 能够容忍部分管理中心的作弊行为. 一张合法的选票只需要经过t个管理中心的签名就可以了. 而且消息块共享保证了当有投票人弃权时, 可以有效地防止签证中心冒名投票的现象.
(10) 抗量子性: 本协议的LTRS 签名是基于格的环签名, 具有抗量子特性.
(11) 实用性: 本协议可将投票人划分为若干个不相交的类别, 可以分别统计每个类别中投票人的观点,也可以像一般的投票方案一样, 统计所有人的观点, 这只需要将最后的投票结果汇总起来就可以了. 无论划分的类别个数是多少, 本协议所需进行的投票轮数都固定不变. 因而本协议满足实用性.
8 结束语
电子投票系统虽然日益完善, 但由于量子计算机的快速发展, 提出一种抗量子的电子投票系统对于电子投票的安全性的保证具有重要意义. 本文提出的LTRS 方案使用消息块共享技术, 在实现中央权力分散的同时满足签名的匿名性, LTRS 方案的可链接性保证签名可被公共验证是否由同一用户生成. 通过安全性分析证明了方案在标准模型下的正确性、不可区分源匿名性、不可伪造性和可链接性. 通过性能分析可知签名算法是多项式时间内可计算的, 并且给出了与其它方案的数据对比结果分析. 本文提出的基于LTRS 签名的电子投票协议可解决多类别投票问题, 该协议满足电子投票协议的八个安全特性和坚固性、实用性和抗量子性, 除此之外, 方案可满足大规模的电子投票需求.

