微网中基于T型三电平逆变器新型双环控制策略
张宏炯,钱叶牛,李鹏飞 ,陈建树,武辰,李涛
(1.国网北京市电力公司通州供电公司,北京 101100;2.国网北京市电力公司,北京 100031;3.上海电力学院自动化工程学院,上海 200090)
随着能源危机与环境污染日趋严重,利用太阳能、风能等可再生资源的分布式发电技术越来越受到人们的关注[1-2]。作为分布式能源系统和大电网间的互联设备,其逆变并网装置的运行性能直接反映了系统功率的输出质量[3-4]。鉴于传统两电平逆变装置存在谐波电流高、电压等级低等缺陷,结合T型逆变装置具有损耗小,高效率等优势[5-8],本文重点利用T型三电平逆变装置来解决上述问题。
目前,分布式系统逆变装置的控制优化策略大多选用比例积分(PI)、比例谐振(PR)和智能算法等优化手段。然而,PI控制系统在控制过程的稳定性较差,且输出电流包含了大量高次谐波[9]。PR优化方法虽能实现系统在特定频率下的无差控制和保持很好的动稳性能,但对非线性负荷的控制而言,其高次谐波的治理效果并不理想[10-11]。预测控制方法能够抑制系统瞬时扰动,但对抑制系统周期性扰动不理想[12]。文献[13]探讨了一种新型电流双环控制策略,其电流内环采用重复PR优化控制法,可对系统电压和非线性负荷的波动进行有效抑制,但该策略下系统的传递函数和阻尼系数很难求解,且优化精度不高。文献[14]提出了滑模变结构因其自适应性强、鲁棒性好、动稳态性能优良等特点备受青睐,但该结构中滑模控制规律设计参数多,很难控制也是不争的事实。为了提高逆变装置的非线性控制优化功能,文献[15]结合Lyapunov函数对并网系统的逆变装置进行控制,既能提高系统功率输出的稳定性又可减少发电系统的谐波电流分量。文献[16]利用Lyapunov函数控制并网系统的逆变装置,从而提高发电系统稳态电流的计算精度。文献[17]综合利用Lyapunov函数和PR控制方法,既保证分布式系统的输出稳定性,又能保证电流的无差控制,从而准确计算出逆变装置的参考电流。
综上分析,本文利用Lyapunov函数提出了T型三电平的分布式系统的并网逆变优化控制策略,并结合并网逆变器的数学模型推导出开关函数的解析式。其次,通过Lyapunov的能量函数设计出分布式系统的电流内环控制器。其中,本系统的电压外环控制器可利用传统的PI控制技术来设计。最后,通过算例结果论证了本文优化策略的合理性。
1 T型三电平逆变器的概述
1.1 T型三电平逆变器的组成
本文选用的T型三电平逆变装置的结构示意图如图1所示。图1中,分布式系统中的三相等效电感和电阻分别为Lf,R;系统的直流侧电压设为Udc;C1和C2分别为系统直流侧的分级电容;uea,ueb,uec分别为系统并网的三相电压;Tx1~Tx4(x=a,b,c)分别为相桥臂开关管;Idc为分布式系统的注入电流。
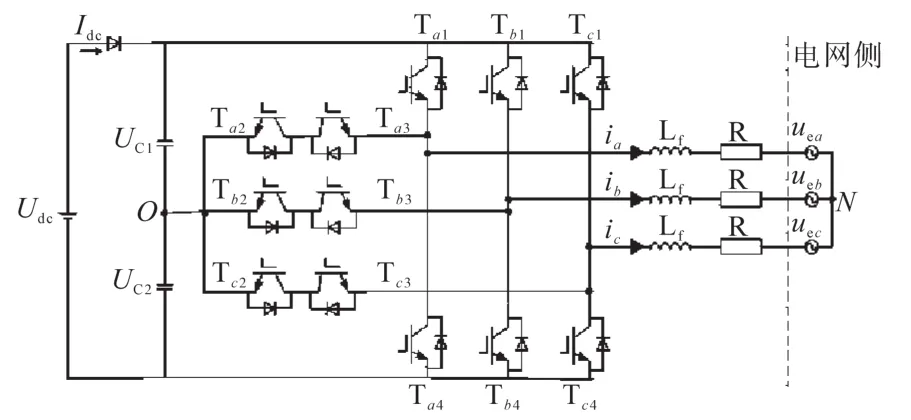
图1 T型三电平逆变装置的结构示意图Fig.1 Structure diagram of T-type three-level inverter device
1.2 T型三电平逆变装置的数学模型
结合文献[5]所述原理,可得到T型三电平逆变装置的数学模型。结合d-q坐标系进行相关变换后,可得到该模型的数学表达式:
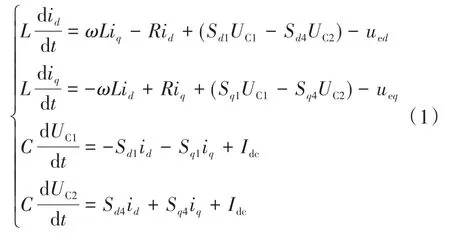
式中:id,iq为三相电流ia,ib,ic在d,q轴上的分量;UC1,UC2分别为分压电容C1,C2的电压;ued,ueq分别为系统侧电压在d,q坐标轴上相应的解析分量;Sd1,Sq1分别为Sa1在d,q坐标轴上的对应分量;Sd4,Sq4分别为Sa4在d,q坐标轴上的对应分量;L为三相线路的等效电感。
2 T型三电平逆变器SVPWM调制算法
设三相输出电压为
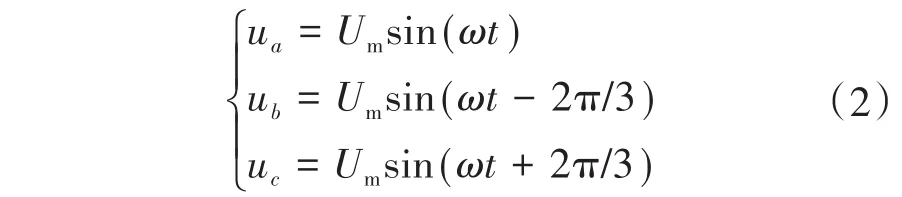
根据abc-αβ坐标变换公式,可得合成空间矢量公式为
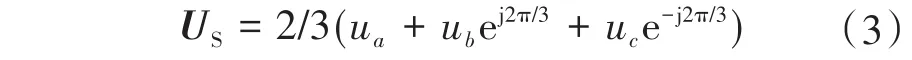
若以图1中的负载中心点N为电位参考点,可知逆变器的三相输出相电压为
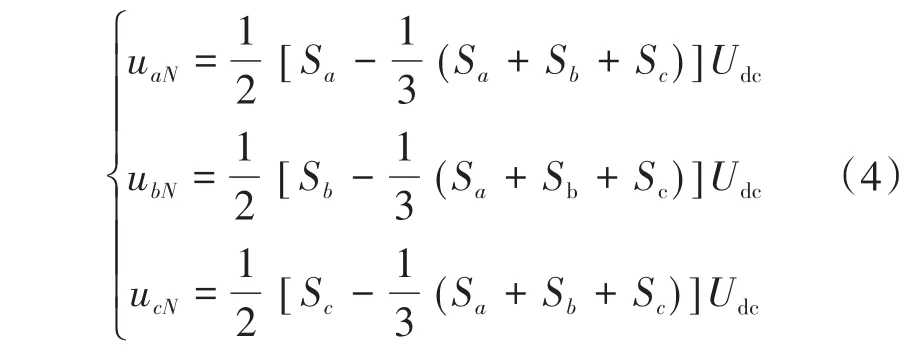
式中:Sx(x=a,b,c)为三相输出的开关变量,其定义为

本文将逆变装置每相桥臂的3种开关状态分别定义为1,0,-1。以A相说明:1表示逆变装置开关管(Ta2,Ta3)同时导通的情况;0表示开关管(Ta2,Ta4)同时导通的情况;-1表示开关管(Ta3,Ta4)同时导通的情况,其余B,C两相情况类似。因此,三相桥臂共计33=27种开关状态。将式(5)代入到式(4)中,即可得到对应于27种不同开关状态组合的空间电压矢量:
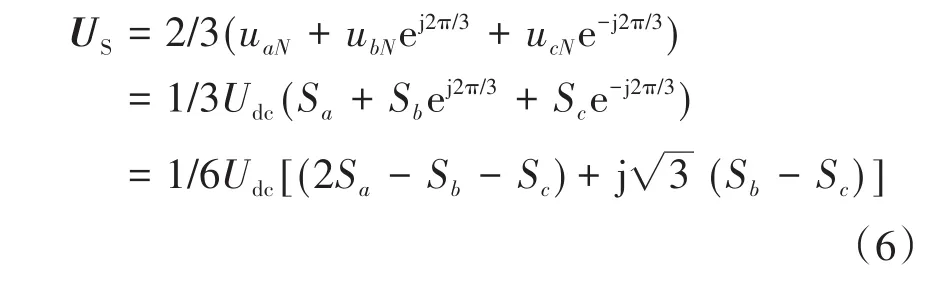
由式(6)可画出T型三电平逆变器的基本空间电压矢量图,如图2所示。

图2 三电平逆变器的基本空间矢量图Fig.2 Basic space vector of three-level inverter
从图2可看出,可将27个电压矢量定义为4类:大矢量、中矢量、小矢量和零矢量,详细分组如表1所示。

表1 空间电压矢量分类表Tab.1 Space voltage vector classification table
总的来说,可认为T型三电平逆变装置的空间矢量调制算法主要分为4部分:空间矢量鉴别区域、矢量状态确定次序、矢量计算作用时间和时间分配状态。
3 电流内环控制器设计
结合文献[18]所述,Lyapunov理论可很好将非线性问题进行相应地线性控制,其控制模型可为
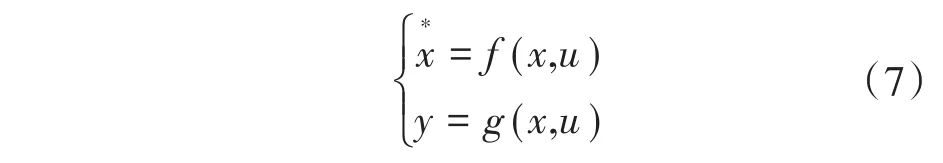
式中:x为系统状态输入量;u为控制量;y为输出量;“*”为一阶导数符号;f(.)和g(.)分别表示系统的控制量、状态量和输出量之间的非线性关系。对其进行泰勒级数展开后可得状态空间模型式为
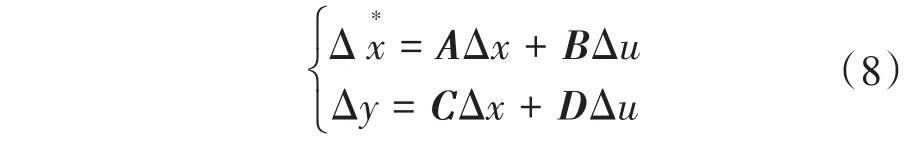
式中:A,B,C,D为相应的常数矩阵。
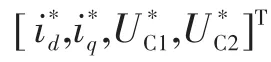
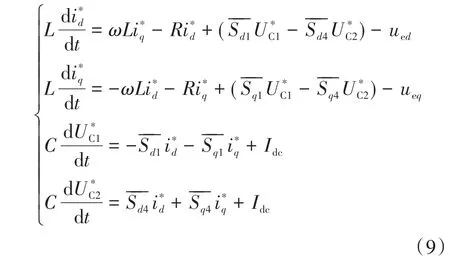
为保持开关函数的对称性,本文结合空间矢量脉宽调制策略对暂态开关函数[15]进行相应修正:
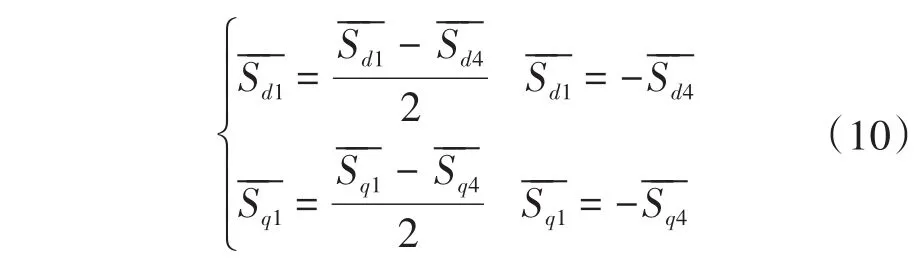
令UC1=UC2=UC,则式(9)可以化简为
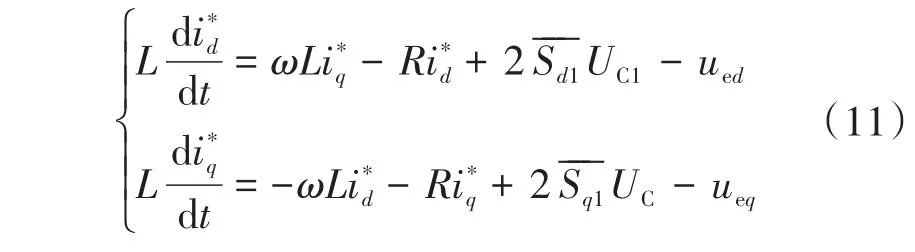
结合式(9)可得暂态时d-q坐标系下开关函数的关系式为
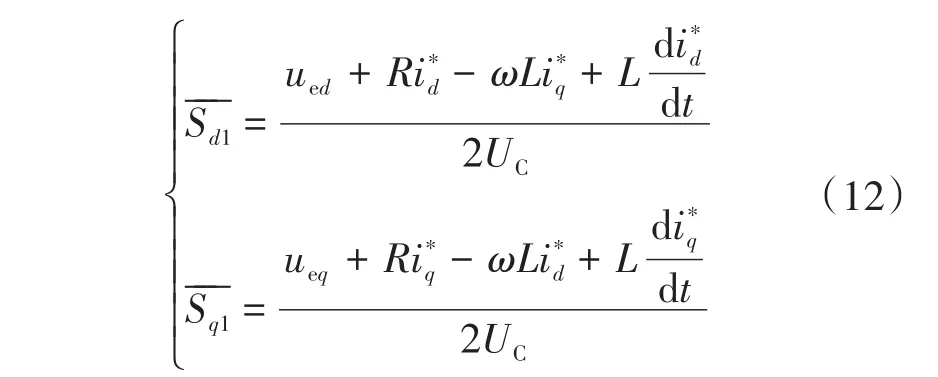
化简式(1)和式(12),可以得到:

式(13)减去式(14),可以得到:
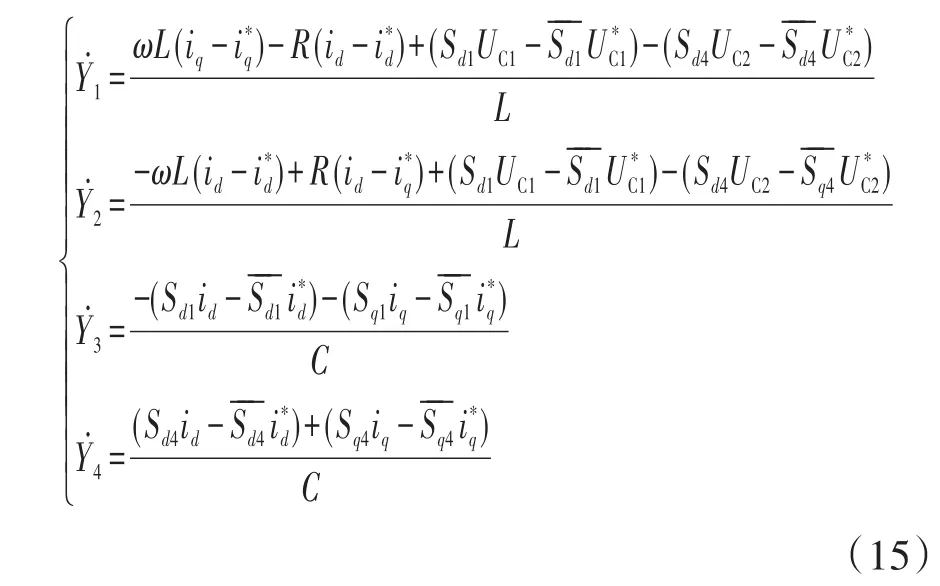
令Lyapunov函数的能量函数H(Y)为
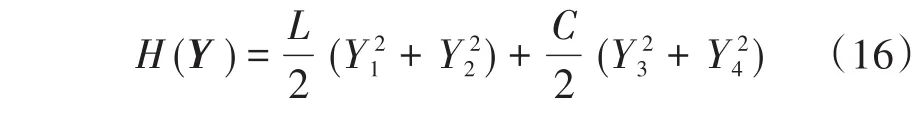
对式(16)两边求导,可以得到:
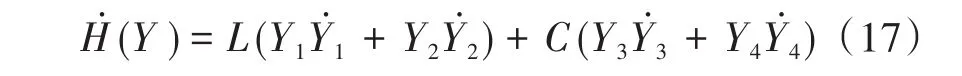
结合式(13)与式(15),可以得到:
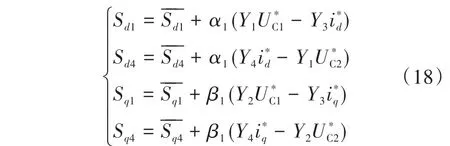
式中:α1,β1分别为d轴、q轴上的控制优化增益部分,其值均小于0。为了保证二者控制的对称性,设定α1=β1。
对分布式能源系统选择相应地控制增益函数,文献[15]已作了详细介绍。
给出Lyapunov函数的T型三电平逆变装置的双环并网控制结构图如图3所示,并选择双环控制算法进行模型的优化求解。其中,利用传统的PI算法进行系统的电压外环控制,其控制输入信号选取为系统直流侧实际的电容电压和设定值之差,从而监测直流侧电压,有效抑制直流侧中性点的电压偏移;此外,选择相应的内环控制的参数为:UC1,UC2,UC1ref,UC2ref,id,iq,idref,iqref。其中,为了保证分布式能源系统以功率因数cosφ=1进行控制,可令iqref=0,而参数idref可结合电压外环计算得到,系统内环控制方法主要是跟踪逆变装置的三相电流和直流电压。
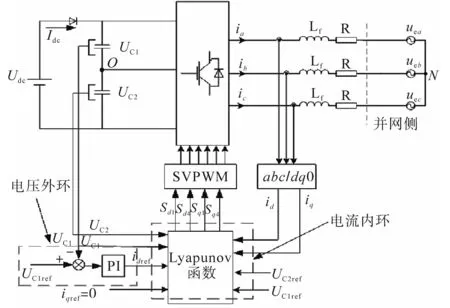
图3 系统控制结构图Fig.3 The diagram of the control method
4 仿真
4.1 本文给出的双环控制系统的仿真结果
结合本文所述的控制原理,在Matlab/Simlink仿真平台上建立Lyapunov函数的T型三电平逆变装置的控制模型,详细仿真参数设置如下:输入直流电压Udc=600 V;直流侧分压电容C1=C2=3 300 μF;滤波电感Lf=5 mH;滤波电容Cf=50 μF;控制增益α1=β1=-0.015;逆变器的开关频率fs=2.5 kHz,电网相电压峰值为311 V,频率为50 Hz。
图4给出了系统电流内环的Lyapunov函数输出函数Sd1,Sd4,Sq1,Sq4,并经dq0-abc坐标系换算出分布式系统的开关函数波形,并将其作为空间矢量调制算法的输入参量,供逆变器桥臂开关动作。图5给出了分布式系统的直流侧电压,如果系统直流侧上下级的电容压差满足±1 V范围内,即说明直流侧中性点电位未发生明显偏移,从而论证所用方法有效抑制了系统直流侧中性点的电压偏移。对模型中两个串联电容选取值有误差时,对系统控制输入的直流电压的影响如图6所示。由图6可知,通过对模型的串联电容在选取不一致问题上进行了分析,当上侧电容电压Ukap或是下侧电容电压Ukan因电容选择误差引起电压偏大时,在系统控制初期会有所上升或下降的趋势,但随着控制时间的增加,系统会形成电压反馈来进行平抑,使得系统控制所需的电容电压维持在合理范围内,从而不会引起控制系统出现电压波动。
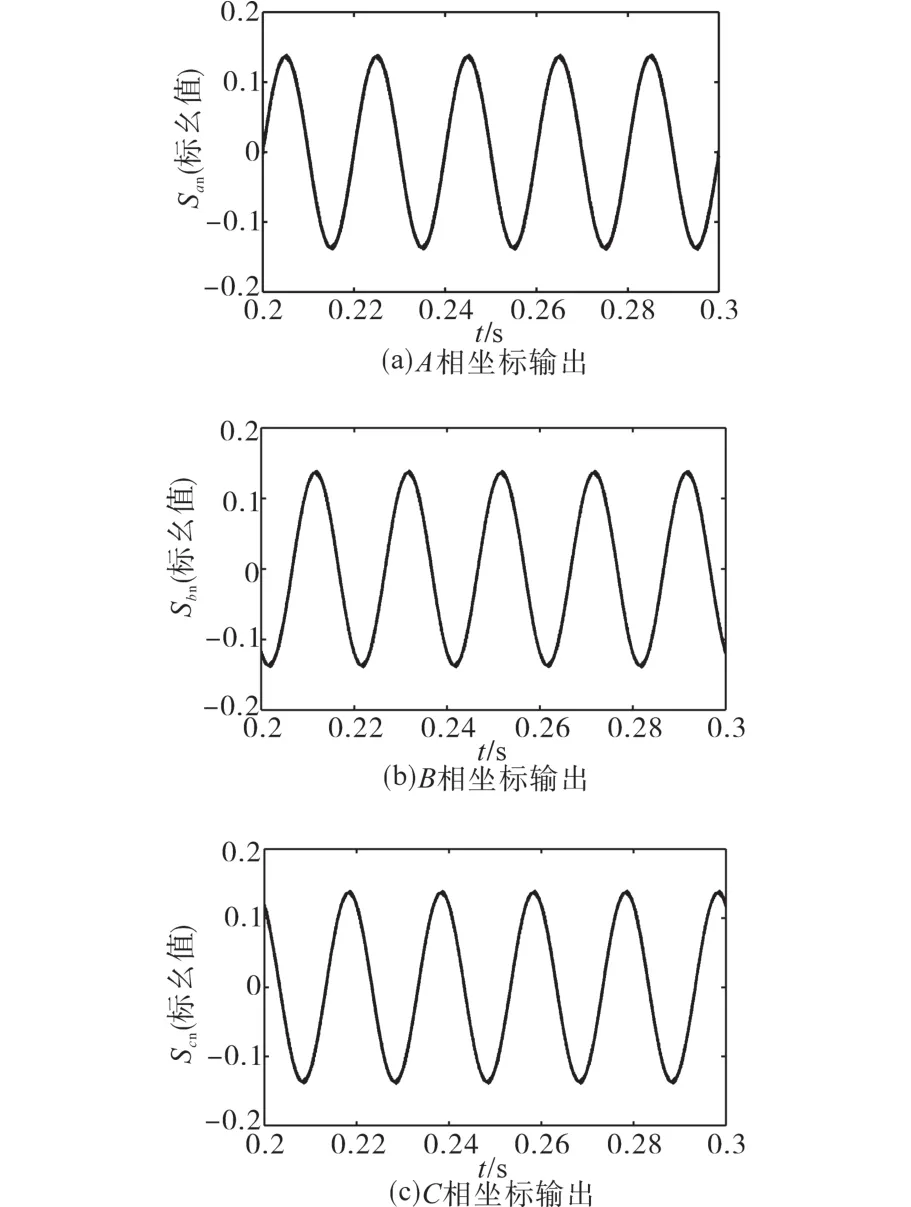
图4 Lyapunov函数控制器输出Fig.4 Output of Lyapunov function controller
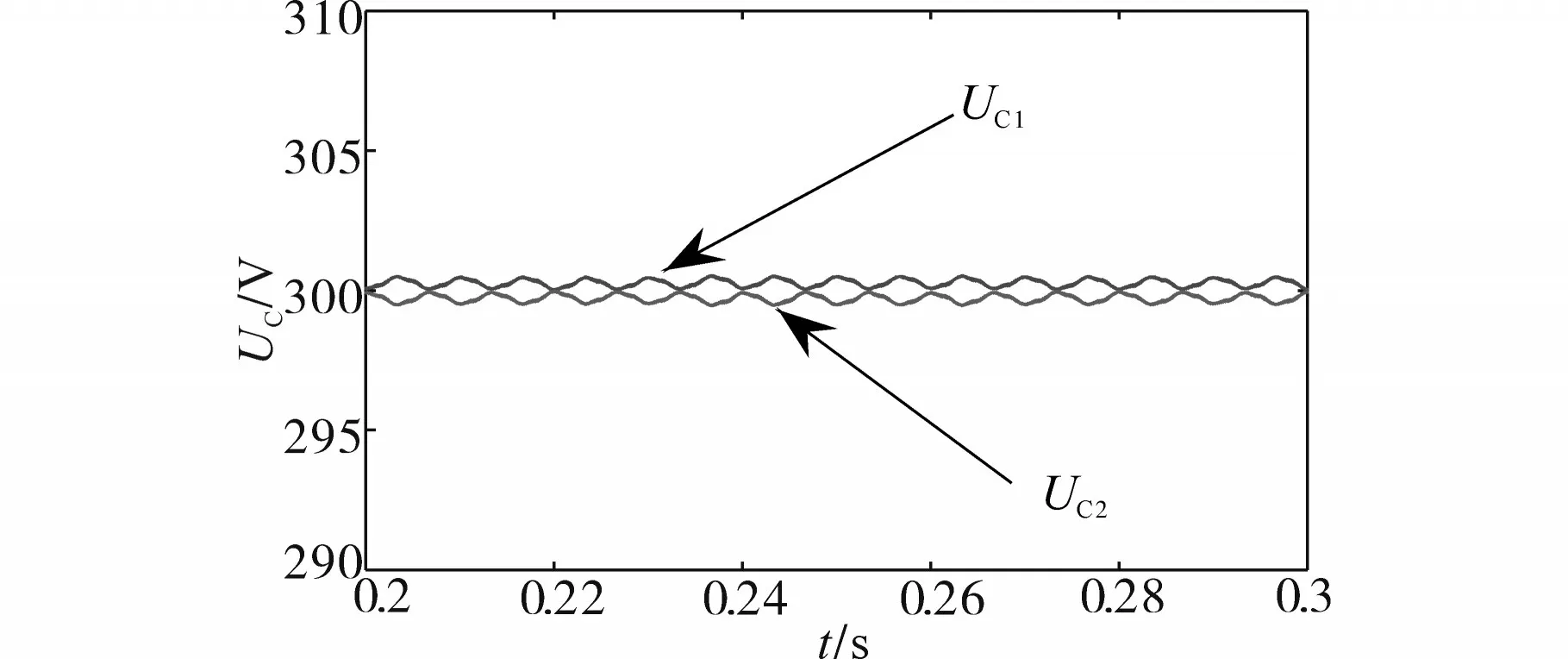
图5 系统直流侧的电容电压Fig.5 Capacitor voltage on the DC side of the system
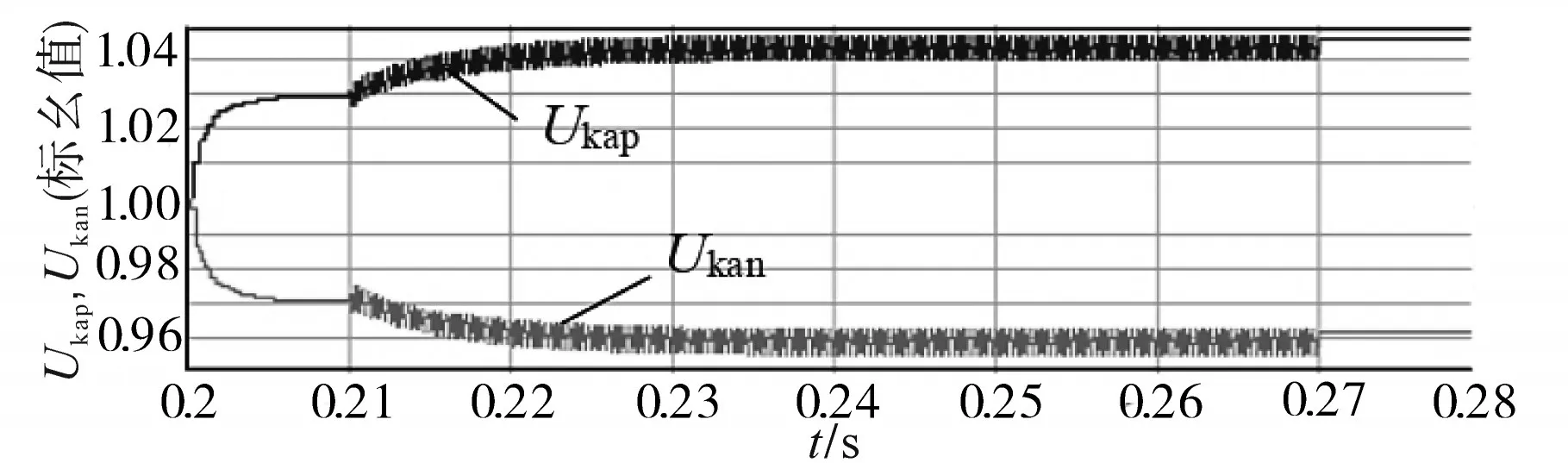
图6 串联电容不平衡引起的电压偏移Fig.6 Voltage offset caused by unbalanced series capacitance
逆变器输出的相电压和线电压如图7所示。由图7可知,并网系统的逆变器输出的相电压数值为:±300 V,0 V,线电压对应的数值为:±600 V,±300 V,0 V,即符合文中所建立的逆变器输出理论下对应的电平数值。
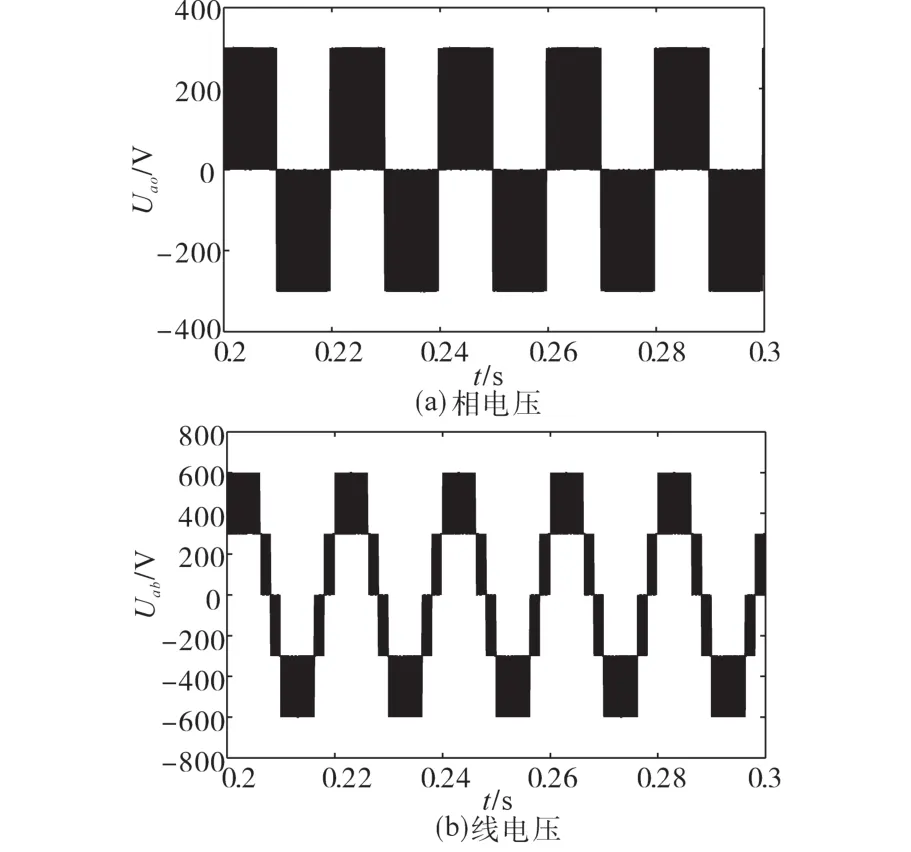
图7 逆变器输出的相电压和线电压Fig.7 Phase and line voltage of inverter
4.2 同传统双PI控制策略的对比结果
为了进一步说明本文控制策略的优势,将其与传统双PI控制优化策略相对比。其中,电压外环与电流内环控制器的参数相等,即Kp=0.8,Ki=5。
图8为两种控制策略下逆变器输出三相电流波形,由图8可知结合Lyapunov函数控制方法后,并网系统输出的电流波形更平滑,即电流谐波分量较少,从而有效验证了电流内环可实现电流谐波跟踪功能。
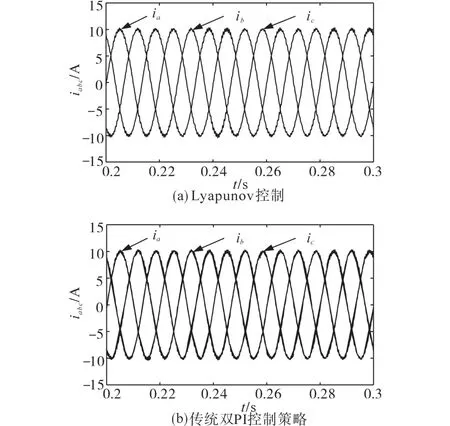
图8 并网系统逆变器的输出电流对比Fig.8 Comparison of output current of grid-connected system inverter
图9为两种控制策略下并网系统A相电压和电流波形,且该两种控制策略都可以实现较高功率因数并网。
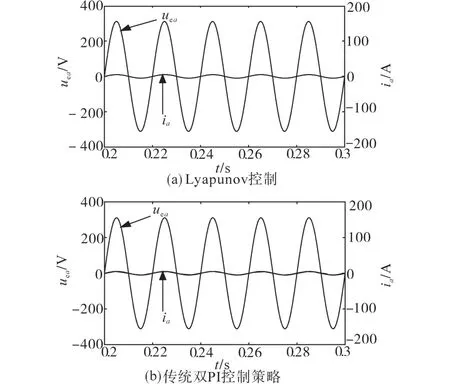
图9 并网系统A相电压和电流Fig.9 A phase voltage and current of grid-connected system
A相电流谐波对比如图10所示。由图10可看出,在两种优化策略下,通过对比A相电流的波形,可得出Lyapunov理论控制下系统的输出电流谐波仅为2.39%,而双PI控制策略下输出的电流谐波为4.19%。从而论证了Lyapunov控制策略对抑制电流谐波、提高电能质量更具优势。
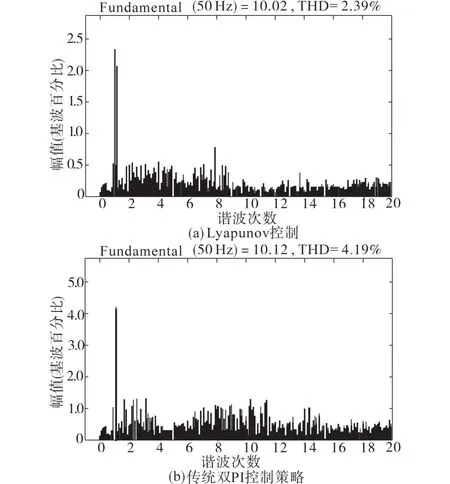
图10 A相电流谐波对比Fig.10 A phase current harmonic comparison
5 实验
本算例在Matlab/Simlink仿真平台上搭建了并网逆变器的控制系统模型,对本文提出的双环控制系统进行实物建模研究,且模型实验和软件仿真设定相同的参数,其实物模型可选择TMS320F28335型的DSP模块生成控制信号,开关器件选择英飞凌IKW40N120H3,并网系统的相电压峰值设定为311 V,频率设置50 Hz。实验的硬件模型如图11所示。

图11 硬件装置照片Fig.11 Photo of hardware device
图12为实验中逆变器输出的系统相电压和线电压波形,并由图12可知该实验结果和软件仿真部分几乎一致,由此说明了本实验平台搭建的正确性。
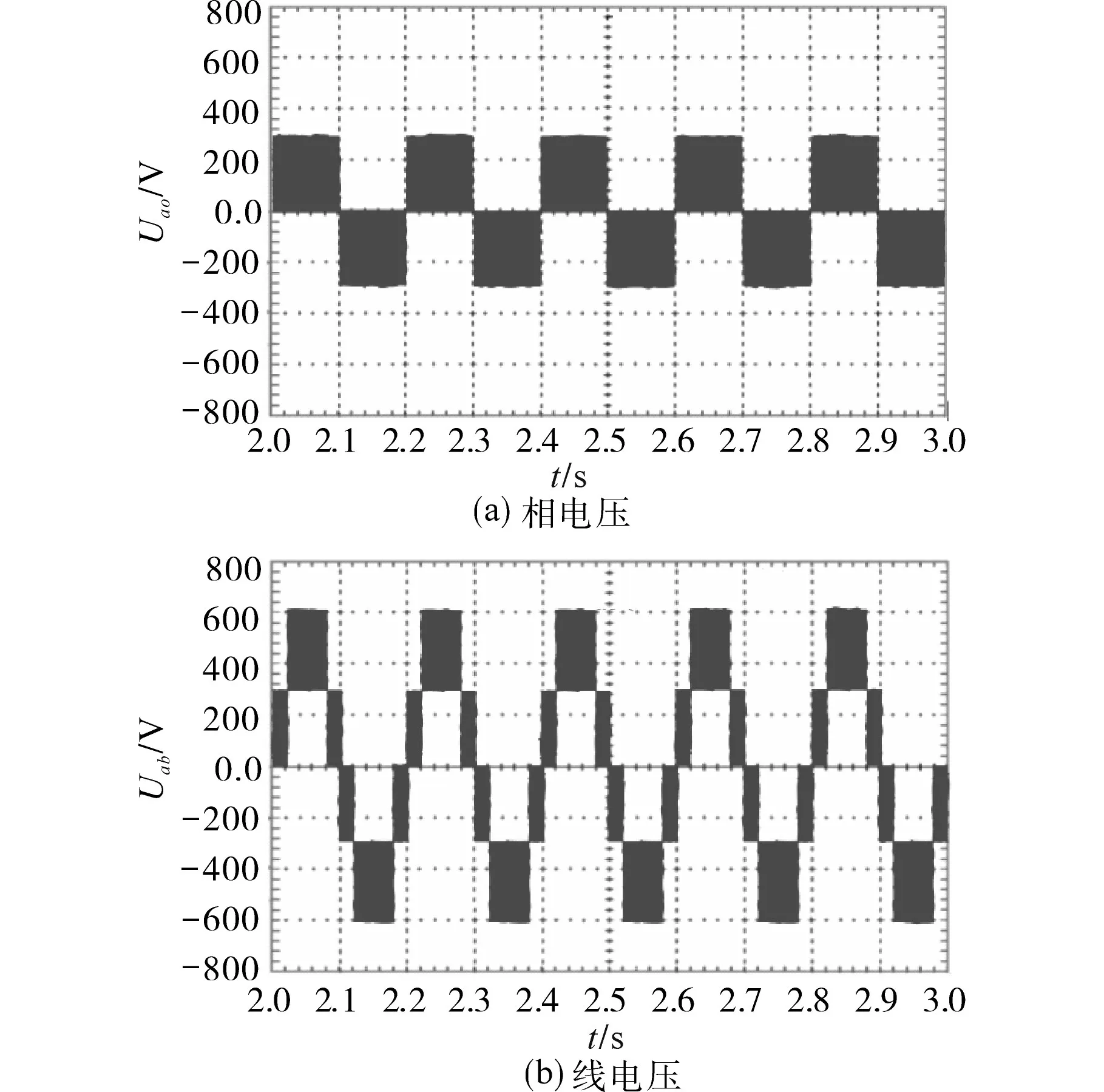
图12 逆变器输出相电压和线电压Fig.12 Phase and line voltage waveform of inverter output
图13为两种控制策略下并网系统的三相电压和A相电流。由图13可知,两种控制策略下并网系统的A相电压和电流的相位基本相同,即两种控制策略均能以较高功率因数并网;但是,从图13b可以看出,在传统的双PI控制策略下,并网系统输出的电流波形所含的谐波较多。由此说明了软件仿真部分即提出的Lyapunov控制策略能有效抑制系统输出的电流谐波。
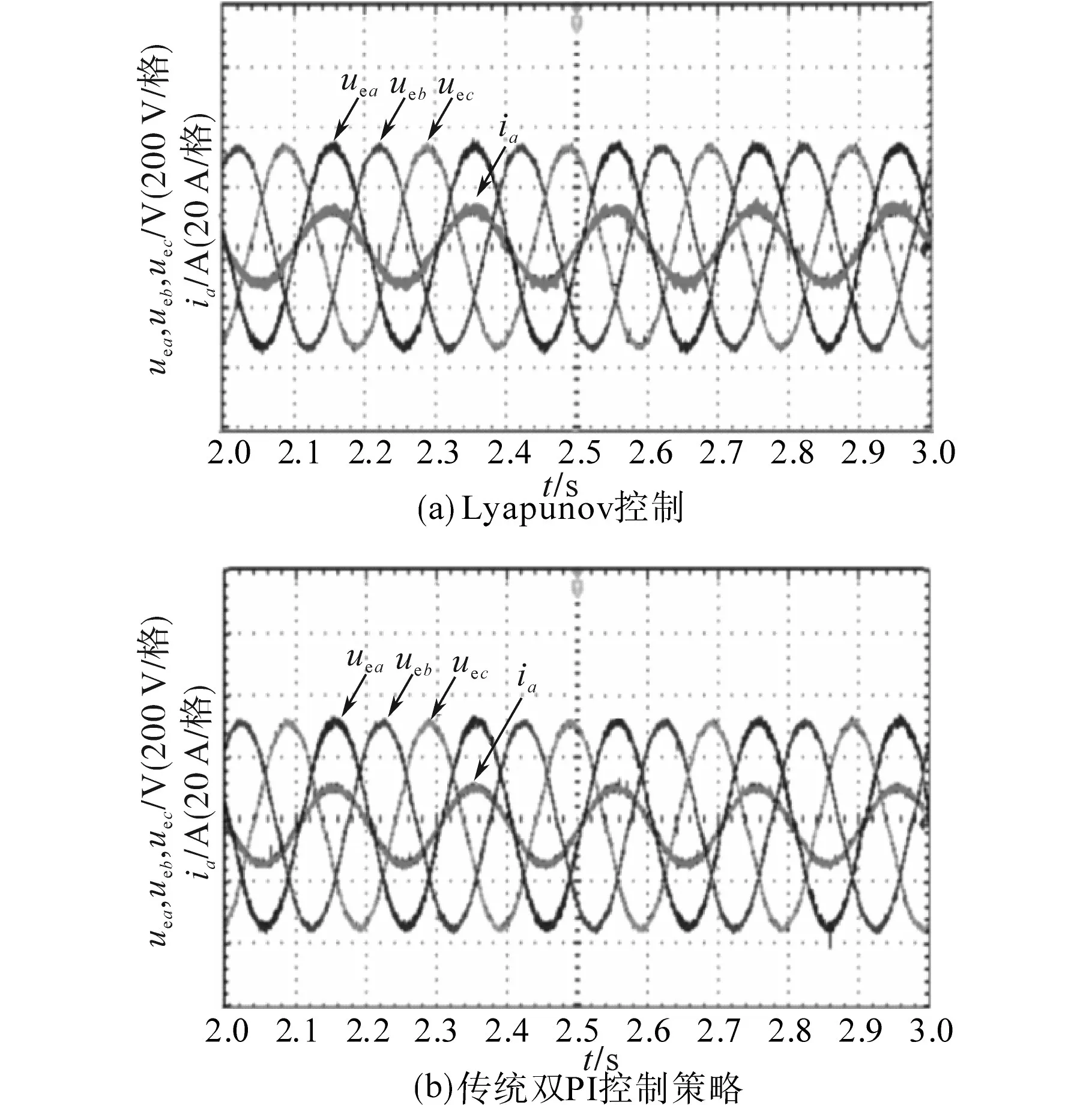
图13 三相并网电压与A相电流对比Fig.13 Comparison of three-phase grid-connected voltage and A-phase current
6 结论
通过本文所提的一种电压-电流双环控制策略,并结合Lyapunov函数对并网系统的电流内环进行相关优化控制,来解决逆变器输出电流的谐波问题;此外,并网系统的电压外环控制可利用传统的PI方法来跟踪直流侧中性点的电容电位。
通过将仿真与实验的结果相比较,得出结论如下:
1)利用Lyapunov函数方法,可有效控制T型逆变器电流内环系统中的直流侧中性点的电位偏移;
2)本文所提的控制优化策略在追踪分布式能源系统的电流谐波方面要优于双PI控制方法,且系统在电能质量方面也能获得很好的控制效果。

