基于VSG的储能功率变流器离网并联控制策略

吴晓丹 ，吴冠宇，周京华，宋强，孙睿

（1.国网内蒙古东部电力有限公司电力科学研究院，内蒙古 呼和浩特 010000；2.北方工业大学北京市变频技术工程技术研究中心，北京 100144）

储能功率变流器（power conversion system，PCS）是储能系统的核心单元，其除了需具备传统的充放电等功能外，对于很多重要工业负荷以及无电的山区海岛等地区，还需具备离网供电功能，以保证电网出现故障时仍能为工厂及数据中心提供应急电源或保证山区海岛居民的正常生活用电，最大程度上降低断电造成的损失。同时，大规模储能系统对储能变流器的容量有了更高要求，因此研究储能变流器在离网下的并联控制也具有重要的现实意义[1]。

当前，多台PCS并联主要包括有互联线并联控制和无互联线并联控制[2]。然而，在实际运行过程中，由于有互联线的并联方式其各个装置间共用一个控制器或者需要高速通信线，因此稳定性较差，且易受到电磁干扰。为了提高并联系统稳定性和冗余性，无互联线并联方式已成为当前各国学者的重点研究内容。相对于有互联线方式，其具有模块间完全独立、抗电磁干扰能力强、能实现并联热插拔等优点。

无互联线并联的基本控制结构如图1所示。

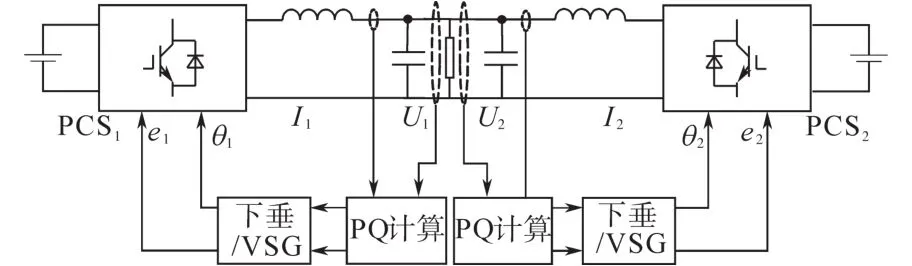
图1 无互联线并联结构Fig.1 Parallel structure with wireless

在无互联线并联控制中，一般采用的是下垂控制策略。然而，传统的下垂控制存在频率变化过快、负载抗扰动能力差等问题。针对上述问题，2008年荷兰学者提出虚拟同步机（virtual syn-chronous generator，VSG）的概念，该方法能够使电力电子装置具备传统同步电机的惯性和阻尼特性。文献[3]通过模拟同步机的二阶电磁模型，使得逆变器获得了传统同步机的电磁特性、转子惯性等。文献[4]利用小信号模型，提出一种基于稳定性的虚拟同步机参数选择方法，且该参数设计方法适用于大部分的VSG控制。文献[5]通过建立并联系统的小信号模型，分析了惯性和阻尼参数对控制效果的影响，并提出一种虚拟惯性量匹配方法。针对VSG控制中惯性参数过大导致的功率振荡问题，文献[6]分析了功率振荡产生的原因，并采用参数设计来减小功率振荡问题，但是该方法采用固定惯性参数设计，不能兼顾抑制功率振荡和保证频率稳定性。基于该问题，文献[7]提出一种基于频率变化的惯性参数调节方法，实现了惯性参数的自适应调节。

针对上述问题，本文在利用虚拟同步机实现PCS并联的同时，提出一种自适应惯性参数调节方法，抑制了PCS并联系统可能出现的功率振荡问题，保证两台装置无互联线并联的同时，又提高系统的抗扰动能力。

1 储能变流器并联系统模型

以两台PCS并联为例进行分析，将每台储能变流器输出侧都用一个电压源来表示，构成并联系统如图2所示。图2中，U1∠φ1，U2∠φ2为PCS离网交流输出电压；U∠0为负载电压；r1，r2，X1，X2为线路阻抗，Z为负载；I1，I2为PCS输出电流。

图2 储能变流器并联系统模型Fig.2 Parallel system model of power conversion system

对交流源并联来说，如果各个装置输出交流电压的幅值、相位和频率完全一致，就能够消除系统内环流。然而由于硬件差异和线路阻抗等因素影响，在实际过程中，各台装置输出电压之间很难达到完全一致，如此就导致了环流的产生。环流不经过负载，而是在装置之间流动。过大的环流会导致功率器件负担增加，严重的则会导致系统崩溃。

2 储能变流器并联控制策略

下垂控制是比较成熟的逆变器无互联线并联控制策略，然而，在很多工业场合中，由于环境的复杂性，负载应用现场存在较多的功率扰动，如果采用传统的下垂控制，频繁的功率扰动很容易导致PCS输出频率的快速变化，严重的可能会对负载造成损坏。因此，本文选用虚拟同步机控制，既实现了装置间的无互联线并联，也使得PCS具备了惯性和阻尼特性，提高了系统稳定性。下面对虚拟同步机控制策略进行分析。

2.1 虚拟同步机控制结构及原理

虚拟同步发电机主要是在下垂控制基础上，利用数字控制器同时模拟出传统同步发电机惯性与阻尼特性的一种控制策略。传统同步发电机由机械和电气两部分构成，通过对传统同步发电机运动方程进行改进，就可以得到虚拟同步机的控制方程[8-10]。

2.2 有功-频率环控制

虚拟同步机频率的调节，是利用虚拟调频器来实现的。通过计算实际输出有功功率与额定有功功率之间的差值，可以对虚拟转矩进行调节：

式中：ΔT为虚拟转矩增量；Pref为PCS额定功率；Pe为PCS实际输出功率；ωN为额定角频率。

虚拟转矩增量就相当于传统同步机中的转矩差，之后ΔT被送入阻尼环节，此时的阻尼D就相当于下垂系数Dp，这样就将传统同步机的有功方程式引入到了电力电子装置中，得到虚拟同步机的有功调频方程，其公式为

式中：ω为VSG输出角频率；J为虚拟转动惯量；D为阻尼系数；δ为2台装置的输出相角差；θ为装置输出电压相角。

将传统同步电机调速控制加入到电力电子控制中，这是构成VSG的重要环节，由此得到虚拟同步发电机的有功功率控制框图如图3所示。

图3 VSG有功控制框图Fig.3 Active power control of VSG

从图3可以看出，具备VSG功能的储能变流器，其输出相位已经不是由控制器中的初始给定值来决定，而是与负载大小、惯性和阻尼参数均相关，这样PCS的相位调节就初步具备了传统同步机的调频特性。

根据图3可得到该控制器的传递函数为

将式（3）化简，可得到：

进一步对式（4）进行变换，得到VSG有功调频环节的标准形式为

从式（5）可以看出，将VSG有功方程写入控制环后，相当于在传统下垂控制中加入了惯性环节，转动惯量J和阻尼D共同决定了频率变化的快慢。而有功下垂系数Dp则由阻尼环节决定，阻尼系数越大，频率变化范围越小。与传统下垂控制相比，由于系统加入了惯性和阻尼环节，使得频率变化速度变慢，增强了系统稳定性。

2.3 无功-电压环控制

传统同步电机通过励磁系统来保证系统输出电压控制在一个合理范围内，并且在并联系统中，能够调整设备间的无功功率合理分配。VSG根据下垂控制原理，同样需要设计出虚拟励磁控制器。首先需要计算装置输出端无功功率的大小，之后将无功功率偏差值经过无功下垂系数得到电压偏差值，该值与电压给定值结合可得到电压外环所需要的电压参考值。无功下垂系数能够准确决定无功功率变化时的电压偏移量，无功功率变大时，电压偏移量减小。

根据下垂原理，可得到VSG在离网模式下无功功率控制框图如图4所示，其中，Qref和Qe分别为装置无功功率给定值和实际的瞬时无功功率，Un和U为电压额定值和电压环给定值，Dq为无功下垂系数。根据图4可得到其控制方程为

从式（6）和图4可以看出，离网模式下，虚拟同步机的无功环与下垂控制中的无功环是一致的，因此VSG的无功调节过程不再赘述。

图4 VSG无功环控制框图Fig.4 Reactive power control of VSG

3 自适应惯性参数调节方法

VSG的应用增加了PCS的惯性，保证系统输出频率在受到功率扰动情况下的稳定性。然而在并联系统中，由于每台装置都采用VSG控制，当负载发生突变时，一旦控制参数设置不合理，很容易引起PCS的有功功率振荡。下面以图2所示的并联模型为例，分析功率振荡产生的原因[11-13]。

设图2中的线路阻抗和负载分别为Z1∠θ1，Z2∠θ2，Z∠θ，通过分析，可得两台装置单相输出的有功功率为

式中：C为PCS并联系统中单台装置等效输出负载的幅值；θC为PCS并联系统中单台装置等效输出负载的相位。

在并联过程中，由于已经进行了预同步环节和增加了虚拟阻抗，因此两台装置输出电压的相位差很小，可认为φ1-φ2=0，且此时装置的输出阻抗为X1∠90°，X2∠90°，由此可近似得到并联装置三相有功功率对输出电压相位的小信号关系为

式中：ΔP1，ΔP2分别为两台装置有功功率的小信号模型；Δφ1，Δφ2分别为两台装置输出电压相角的小信号模型。

根据式（8），得到VSG两台装置实际有功功率与角速度的小信号模型为

式中：J1，J2分别为两台PCS的惯性参数。

由于两台装置的VSG参数基本一致，因此式（9）中存在J1=J2=J，D1=D2=D，令Δω=Δω1-Δω2，Δφ= Δφ1- Δφ2，可得到VSG并联系统中两台装置的二阶系统模型为

求得该二阶系统的特征根为

其中

式中：ξ为阻尼比；ωn为自然振荡频率。

由式（12）可以看出，阻尼比ξ与惯性参数J和阻尼D均相关，增大D或者减小J都可以增大阻尼比，进而可减小超调量。结合对式（5）的分析可知，VSG的惯性参数越大，系统动态响应时间越长，频率变化速率越慢；惯性参数越小，系统动态响应时间越短，频率变化速率越快。然而，并非是惯性参数越大，系统越稳定。过大的惯性容易导致系统出现功率超调，造成功率振荡。惯性参数越小，虽然能够提高并联系统的动态响应速度，但是会导致系统惯性减小，在功率变化过大的条件下，频率变化速度也会加快，进而造成系统输出频率的不稳定。

因此，对VSG参数的设计需要能够兼顾抑制功率振荡以及提高频率稳定性的需求。从式（12）可以看出，减小J和增大D都能抑制功率振荡，然而阻尼D影响的是VSG的频率调节范围，在PCS运行标准的限制下，D的取值最好不要发生改变，因此本文主要是对惯性参数进行调节。

基于上述问题，本文对文献[7]中方法进行改进。由于系统输出的频率变化量与功率变化量呈正相关，如果功率变化量小，则频率变化量也小，因此本文提出一种基于功率的自适应惯性调节方法，使得惯性参数可以根据功率变化量进行自主调节，如下式：

式中：J0为不产生功率振荡的初始惯性参数；k为功率跟踪常数；n为功率限定值，其数值由负载对频率的耐受能力来决定；Δpe为功率变化量，其最大值为1。

在整个二阶系统中，当选取ξ为0.4～0.8时，超调量介于1.5%～25.4%之间，此时系统超调量适中，响应速度快[13]，因此对惯性参数J的设计应该使得ξ在规定范围内，由此可得到超调量在1.5%时惯性参数的计算公式为

此时的J就可以作为式（13）中的最小惯性参数J0。

当超调量在25.4%时，可得到此时的惯性参数为

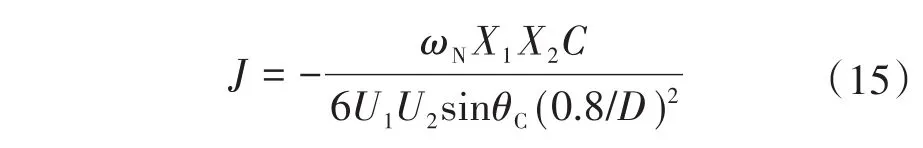
此时由于惯性参数较大，因此系统惯量增加，系统稳定性也提高。

得到最大惯性参数和最小惯性参数之后，结合式（13）就可以得到功率跟踪常数k的值为

根据式（13），可以得到利用该参数调节方法的运行逻辑为：1）当两台装置并联或外部功率扰动量较小时，J=J0，此时由于惯性参数较小，因此并联系统不产生功率振荡，且此时的频率变化量也小，不影响系统输出电压的稳定性。2）当两台装置负载扰动量较大或者并联系统有装置大功率切除时，J随功率变化量的增加而变大，使得系统惯性增加，提高了系统输出频率的稳定性。

4 实验结果分析

为验证上文提出的控制策略，本文进行了VSG并联的实验。

首先进行固定惯性参数下的VSG空载并联实验，其实验波形如图5所示。从图5中可以看出，由于固定惯性参数J比较大，且在并联继电器闭合时，电压幅值和相位仍存在微小差异，使得系统在并联瞬间出现一定的电流冲击，因此VSG的并联过程出现一定的功率振荡，经过大约Δt1的调节时间后才实现稳定空载并联，此时Δt1为1 s。可见，虽然较大的J能够提高VSG输出频率的稳定性，但影响了并联动态性能。

图5 固定惯性参数下空载并联波形图Fig.5 No load parallel waveforms with fixed inertia

采用基于功率的自适应惯性调节来进行空载实验，其实验波形如图6所示。由于自适应惯性参数J与有功功率变化量有关，因此在系统空载并联时，功率变化量很小，此时的J为不产生功率振荡时的惯性参数J0。由图6可以看出，采用自适应惯性参数调节后，并联系统功率振荡的动态时间明显加快，经过Δt2约为200 ms的时间就基本实现了空载并联，证明了该自适应惯性参数调节方法具有较快的动态性能。

图6 自适应惯性参数下空载并联波形图Fig.6 No load parallel waveforms with adaptive inertia

对于VSG带载并联，其实验过程和空载并联基本一致。首先进行固定惯性参数下的带载并联，其电压电流波形为图7所示。从图7中可以看出，两台装置预同步完成之后，由于交流电压幅值和相位仍存在微小差异，且固定的惯性参数较大，因此，系统并联瞬间会经过大约Δt3时间的功率振荡过程，此时Δt3约为300 ms，之后两台装置依据VSG参数设定值达到功率均分的效果。

图7 固定惯性参数VSG带载并联波形图Fig.7 Loading parallel waveforms with fixed inertia

采用自适应惯性参数调节方法来进行VSG带载并联实验，其实验波形如图8所示。与空载并联情况类似，由于此时的功率变化量小，此时的J仍然是一个较小的值，不易产生功率振荡。由图7和图8对比可以看出，采用自适应惯性调节后，两台功率并联振荡的动态时间明显加快，大约Δt4约为150 ms的时间就基本实现了带载并联，证明了该自适应调节方法的有效性。

图8 基于自适应惯性参数带载并联波形图Fig.8 Loading parallel waveforms with adaptive inertia

5 结论

以储能功率变流器为研究对象，建立了两台装置的离网并联等效物理模型。针对有互联线并联控制和传统下垂控制的不足，本文重点研究了VSG控制的原理；针对VSG控制中出现的功率振荡以及并联响应时间过长等问题，提出一种自适应惯性参数调节方法，使得VSG策略既能实现无互联线并联，又能提高系统的并联动态响应。最终的实验结果也进一步验证所提控制策略的有效性。