倍压整流电路在DC/DC大升压比电路中的应用

张国森，张一鸣，张云睿，高俊侠

（北京工业大学信息学部，北京 100124）

截至2017年底，我国累计探明石油储量389.65 t，同期原油对外依存度高达67.4%，预测该数字在2035年将达到76%[1]。油气资源的稳定供应事关国家经济安全，储层评价技术近年来发展迅猛，其中核磁共振技术已经成为油藏描述的重要物理工具。得益于近30 a来电力电子技术的发展，核磁测井技术也取得了一定的突破，但国内对随钻核磁测井技术的研究仍处于相对落后的状态。

1 核磁共振技术在石油探测领域的发展

核磁共振测井（nuclear magnetic resonance logging，NMRL）技术与医学磁共振成像（magnetic resonance imaging，MRI）是一样的原理，即梯度磁场和射频线圈发射交变电磁场来实现空间定位和选片。但在设计上则进行了彻底的改造，即不是把观测样品放在仪器（磁体）的中心，而是把测量仪器（磁体和天线）放在井眼之中，地层作为观测样品则处于仪器的外面。核磁共振测井技术相比其他单一测量技术，例如方位声波测井、方位密度和伽马能测井、中子孔隙度测井等能提供更丰富的地层参数[1-2]。随着钻井深度的不断提升，核磁共振测井技术已经从电缆测井向随钻测井发展，在随钻核磁共振测井领域，国外处于领先地位的钻井服务公司如哈利伯顿及贝克休斯早在2001年就相继推出了成熟的技术方案，但仅提供商业钻井服务[3]。目前国外处于领先地位的随钻核磁共振测井技术公司包括哈利伯顿、贝克休斯及斯伦贝谢。极端条件下的核磁共振测井发射电路，能够深入到探测目标内部建立发射条件，发射电路的设计是一个测控电子工程问题，包含模拟电路与数字电路的优化设计及元器件的优选。与极端环境下核磁共振测井探头的探测特性相对应，探测对象的复杂多样、含量少、体积受限、低场、单边测量、探测深度大等，都对发射电路提出了苛刻要求[4-5]。我国的核磁共振测井技术研发起始于1996年，目前在电缆测井方面已经有成熟的技术方案，并且已经实现了实井的钻探，但随钻测井技术目前仍处于探索阶段，与国外随钻核磁共振测井仪研发相比，我国在这方面与国际先进水平还有很大差距。

随钻核磁共振相比电缆核磁共振，主要难点在于井下直流电源部分的设计，该部分电源需要将涡流发电机提供的直流电升至发射所需的电压，同时要求该电路在150℃环境下稳定工作。国内关于该部分的论文讨论较少，很多工作需要自行摸索。近年来已经提出了很多改进拓扑结构的DC/DC开关电源，这些拓扑的目标都是为了实现高效率，简单结构和低成本[6]。如下图1移相全桥拓扑在内的各式软开关电路可以减轻元器件的电流-电压应力，然而它也有一定的局限问题——零电压开关技术（zero voltage switching，ZVS）开通范围窄、次级整流器的谐振问题、占空比丢失问题等[7]。

图1 移相全桥拓扑Fig.1 The topology of the phase-shifted full bridge

在需要维持功率模块的高压应用的情况下，整流二极管的电压振铃问题往往很严重，虽然可以通过添加用于吸收整流管振铃的电容-电容缓冲器为缓解震荡，但这会导致系统的效率变差，在能量宝贵的井下设备中，这是应当极力避免的。受限于高温器件在控制方式上的限制，重新审视传统的开关电源拓扑，通过双极性控制的方式，并将传统的全桥整流重新设计为倍压整流方式，省去了笨重的LC滤波输出，简化了整体的结构。倍压整流方式下，因为无需大的输出滤波电感，可以采用额定电压较低的整流管，无需添加阻容缓冲器以提高效率。同时通过电容和变压器漏感之间的谐振调整电流波形以优化电路的整体效率。

2 倍压电路的发展及工作原理

在DC/CD开关电源中，为了获得较高的输出电压，往往通过提高变压器变比的方式，但这种方式带来的问题是在高变比情况下，变压器次级侧的匝数过多，除了导致体积变大外，变压器寄生参数带来的影响也是不可忽略的[8]。因此在这种情况下，采用倍压整流的方式，可以使较低的次级侧电压变为更高的输出电压。

常用的倍压电路基本结构包括以下两种：信克尔及科克罗夫特-沃尔顿对称式多倍压整流电路，图2 a、图2b分别为其原理图[9]。

图2 常用倍压电路Fig.2 Common voltage doubler circuit

本文中仅对2倍信克尔倍压电路进行分析，其工作原理简述如下，负半周D1导通，开始对电容C1充电，假设D1导通对C1充电电压为V，那么在正半周导通时，变压器次级电压和电容C1一起对C2充电，C2两端电压为次级侧电压和电容C1的电压和即为2V。沃尔顿倍压电压原理与此相似，但无论是哪个电路，其输出电容的电压都会是2倍的次级侧电压，在高压应用乃至高温应用场合，不一定有足够大容值的电容可供选择。因此相较之下，本文中的二倍压电路设计中，两个倍压电容的电压均为次级侧电压，有利于电容的选型。

双极性控制情况下，电路工作原理较为简单。电路拓扑如图3所示，Q1～Q4为4个开关管，假设开关管和整流管都为理想器件，忽略变压器漏感影响，在一个开关周期经历3个开关模态。

图3 倍压整流电路Fig.3 Voltage doubler rectifier circuit

2.1 开关模态1

图4为开关模态1电路示意图，其中，开关管Q1，Q4导通（见图4中粗线部分），Q2，Q3关断，变压器二次侧感应电压为E/n，E为输入电压，n为变压器变比，且上正下负，整流二极管D1导通，对电容Co1充电，Co1电压为E/n。

图4 开关模态1Fig.4 Switch mode 1

2.2 开关模态2

图5为开关模态2电路示意图，其中，开关管Q2，Q3导通（见图5中粗线部分），Q1，Q4关断，变压器二次侧感应电压为E/n，且下正上负，整流二极管 D2导通，对电容Co2充电，Co2电压为E/n。

图5 开关模态2Fig.5 Switch mode 2

2.3 开关模态3

图6为开关模态3电路示意图，其中，开关管Q1，Q2，Q3，Q4关断，整流管 D1，D2关断，电容向负载输出能量（见图6中粗线部分）。

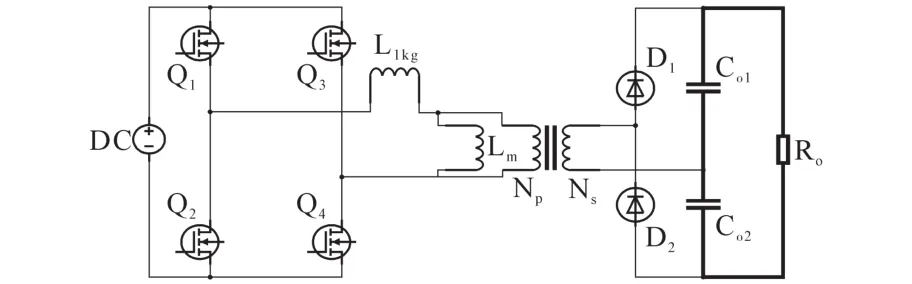
图6 开关模态3Fig.6 Switch mode 3

3 电路参数对电流及电压波形的影响

3.1 DC/DC升压比的计算

为了更简单的推导出转换比，忽略开关模态3的时间（开关模态3在整个开关周期所占的时间极短）。在开关模态1中，流过D1的电流可以通过下式得到[10]：

式中：Vin为输入电压；n为变压器变比；Vo为输出电压；ID1为二极管D1电流；Z0为图3所示电路等效阻抗；t0为起始时刻。

在开关模态1中，可以看到，Co1的充电电流和Co2的放电电流都流过D1，同时Co2的放电电流等于负载电流，所以半个开关周期内，ID1的平均值等于负载电流Io的两倍。同样的在另外半个开关周期内，Co2被类似的充电，Co1需要提供与负载电流相同的电流值。因此电容Co1的电压变化值ΔVo1可以推导如下：

式中：Ico1为流过电容Co1的电流；Ts为系统的周期。进一步，通过式（2）及输出电容Co1的偏置电压Vo1_bias可以得到电容Co1的电压Vo1表达式为

通过计算整流管的平均电流，可以得到负载电流为下式：

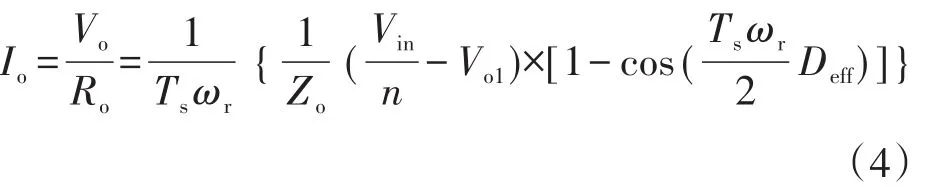
式中：ωr为系统的角频率；Deff为占空比。

综合式（3）、式（4），根据系统的工作频率F可以计算得到稳定状态下电压转换比：

事实上，由于采用倍压整流方式，变压器副边在开关管全部关断时，副边电压不为零，被倍压电容钳位，因此相比于全桥或半波等整流方式，其输出电压和占空比大小的线性度较差，容易出现占空比较小的问题[11]。因此系统在50%负载时，占空比应当处在一个合适的区间，防止过小占空比带来的过流或损耗发热等问题。

3.2 谐振对电流峰值的影响

由于变压器副边采用倍压整流的方式，导致了整流管电流应力会变大，这是由于在相同功率下，变压器副边电压仅有输出电压的1/2，进而要求副边电流需要加倍。然而可以利用漏感和整流管之间的谐振降低整流管的电流应力及开关回路的开关损耗。图7对不同开关频率情况下的电流波形进行比较，由于电路的负载是相同的，因此每种情况下，流过电流的平均值应当是相同的。在图7a中，谐振频率远小于开关频率，电流波形近似直线型，图7b和图7c中，当谐振频率低于开关频率，并逐渐增大时，电流波形更接近完整的谐振波形，并随开关管关断而截止。在图7b中，谐振频率略小于开关频率，由于电流的平均值应当是相等的，所以准正弦波形的峰值应当小于直线的峰值。当谐振频率超过开关频率时，电流波形如图7c所示，电流波形变为正弦波形的正半周期，显然同样为了平均电流的一致，正弦波形的峰值会大于准正弦情况。因此根据开关频率，适当的确定谐振频率，有利于减小整流管的电流应力，同时让开关回路在开通和关断时尽可能减小峰值，可以有效地降低开关管的开通和关断损耗[12]。最后有利于减轻串联扰动、增加电路的可靠性。

图7 谐振电流与开关频率的对比Fig.7 Comparison of resonant current and switching frequency

4 实验验证与结果

为验证上述拓扑的特性，按照以下参数设计开关电源拓扑：输入电压Vin=85～95 V，输出电压为Vout=600 V，最大功率Pmax=250 W，开关频率Fs=100 kHz，变比1∶n=1∶3.5，漏感Likg=0.22 µH，电感Lm=782µH，倍压电容容值Co1=Co2=1.0µF，开关管Q1～Q4SCT20N120，整流管 D1～D2C4D1012E。设计实验室原理样机如图8所示。

图8 实验室原理样机Fig.8 Laboratory prototype

变压器磁芯的选择以平面变压器为主，如EQ或ER型磁芯。死区时间由控制芯片与开关频率共同决定[13]。

PWM脉宽调制电路由UC3525双极性控制芯片、TL431可控精密稳压源及PC817b线性隔离光耦组成。其中UC3525芯片广泛应用于开关电源的调压及稳定控制，它包括了推挽输出、高精度基准电压源、欠压锁定和误差放大器等功能[14-15]。通过PC817b和TL431组成的隔离反馈防止高压输出对输出造成影响，并在TL431输入侧构成局部PI反馈增加电路调整的快速性和稳定性。反馈电压通过隔离光耦直接送入UC3525的误差放大器输出端。

图9为控制及反馈电路的原理图。

图9 控制及反馈电路原理图Fig.9 Schematic diagrams of control and feedback circuit

图10为带载情况下的电流与电压实验波形，其中整流管的电流波形如图10中通道4波形呈现准正弦波形，因此整流管与开关管均只有较小的导通与开关损耗。同时图10中通道1波形为输出电压，通道2及通道3分别为变压器复变电压和MOS管驱动波形，最终的输出不带LC滤波输出，整流管上的电压始终钳位到输出电压，而没有高压振铃。

图10 实验波形Fig.10 Experimental waveforms

5 结论

本文所采用的倍压整流方式，采用双极性控制的方式，通过调整谐振参数，使得电流波形接近准正弦波形，降低整流管及开关电路的电流应力。同时抛弃传统的LC滤波输出，使得系统的复杂度降低，结构简单轻便，没有输出电感的同时整流管没有高频振荡，可以采用更低耐压的整流管以方便选型，也省去了RC缓冲器。系统在200 W负载情况下，输出效率达到90%，在20℃室温环境下，开关管自然散热条件下温升为30℃，因此本文所采用的转换器因其高可靠性、高效率证明了其在高升压比电路中的适用性。