基于多元统计分析绝缘纸工频击穿强度影响因素的研究

吴东乐 刘群华 孙胜然 徐凯丽 刘 文，*

（1.中国制浆造纸研究院有限公司，北京，100102；2.国家纸张质量监督检验中心，北京，100102；3.制浆造纸国家工程实验室，北京，100102）

随着特高压输变电工程的大规模建设，电工绝缘材料的需求呈现阶段式增长，作为一种优良的绝缘材料——纤维素绝缘纸的性能及其油纸复合绝缘体系性能的提升面临巨大挑战［1］。此外，由于油纸绝缘体系的复杂性，能否获得更准确的影响机制和计算方法，以缩短电力装备的研发周期并降低成本，是研究人员长期面临的重要问题。工频击穿强度是绝缘纸的宏观电气性能，这与纤维形态和纸张结构密切关联，准确分析绝缘纸工频击穿强度的影响因素，并对击穿强度进行预测和工艺优化研究，有助于提升特高压变压器用绝缘纸产品的制造技术和质量水平。

植物纤维形态包括纤维长度、纤维宽度、纤维壁厚和细胞腔直径等参数［2］，纤维形态对绝缘纸的多种性能影响显著。黄建文等［3］研究针叶木原浆种类对绝缘纸击穿性能的影响发现，不同种类针叶木浆的纤维形态不同，相应制得的绝缘纸在油中的击穿强度也不同。Zhou等［4］采用多元统计分析方法研究纤维形态各项参数对直流电场下绝缘纸击穿强度的影响；结果表明，纤维长度和细小纤维含量对其击穿强度影响显著。

从绝缘纸的击穿理论来说，绝缘纸是由纤维相互交织、层叠而成、具有三维多孔结构的材料，在纤维网络内部有大量的孔隙；因此，无论以油浸渍还是以原有状态进行击穿强度实验，实际上都是对由固体纤维和液体或气体等绝缘介质组成的混合结构进行的实验［5］。因此，在研究绝缘纸击穿强度性能的影响因素时，必须考虑这种混合结构。纸张结构可以用紧度、孔隙率、透气度和孔径分布等指标进行描述，这些指标从不同的角度描述纸张结构特性［6］。针对纸张的多孔结构，Mohanty等［7-10］通过在薄膜上制造出一个圆形孔，将其放在绝缘纸上来模拟绝缘纸的孔隙局部放电，采用模糊逻辑方法、多层前馈网络、径向基函数网络和人工神经网络等软件计算技术，分别对几类绝缘纸的击穿电压进行建模，并针对直流和交流电压条件提出了不同的预测模型；结果表明，建立的预测模型能够较好预测绝缘纸的击穿电压。Ghosh等［11］则通过人工神经网络模型研究了绝缘材料的孔隙尺寸和厚度与其局部放电之间的关系。以上研究都是基于在薄膜上制造一个圆形孔，其大小取决于所制造孔的直径和薄膜的厚度；但实际上，绝缘纸内部的孔隙具有不同的几何形状，并且分布随机。所以，以上研究与实际情况存在差异。Singh等［12］以厚度、相对介电常数、损耗角正切和体积电阻率为参数，利用人工神经网络预测纤维素绝缘材料的击穿强度，取得良好的预测结果，但研究存在神经网络模型运用较为复杂的问题。

基于变压器体系特性，以及各影响因素与击穿强度之间的复杂关系，可以采用灰色关联分析（GRA）量化各影响因素与击穿强度之间的关系。王雁凌等［13-14］采用GRA方法构建了一种模型，模拟电力系统中电力负荷和输电线路的损耗与各影响因素之间的关系。

本课题根据GRA理论，研究纤维长度、纤维宽度、细小纤维含量、厚度、紧度、孔隙率和透气度与绝缘纸工频击穿强度的灰色关联度，构建工频击穿强度影响因素量化分析模型，明确各因素对工频击穿强度的影响机制；其次，采用多元统计分析方法中的主成分分析和最佳子集选择方法构建工频击穿强度的预测模型，可以对产品性能进行预测，预先做出风险评估，并指导绝缘纸的研究和生产。

1 实验

1.1 实验原料

纤维原材料采用加拿大Canfor公司的未漂白针叶木硫酸盐浆，灰分0.43%；用于浸渍的变压器油选用北京欣环诚油脂分装有限公司的25#变压器油。

1.2 样品的制备

本课题通过正交实验，对打浆度、打浆负荷、定量与干燥方式4个因素进行设计并制备相应的绝缘纸样品，实验方案如表1所示。将绝缘纸样品置于105℃烘箱内烘干4 h，并将变压器油预热至70℃，然后将变压器油倒入盛有绝缘纸样品的容器中，在真空条件下浸渍48 h，浸油完成后除去绝缘纸样品表面多余的变压器油，将样品放置于密封袋中保存。

1.3 纤维形态和纸张结构参数测试

采用瑞典L&W公司的纤维分析仪测定纤维的长度、宽度和细小纤维含量；按照GB/T 451.3—2002测定绝缘纸的厚度和紧度；采用全自动真密度分析仪测定绝缘纸的孔隙率；按照GB/T 458—2002测定绝缘纸的透气度。

表1 实验方案Table 1 Experimental scheme

1.4 工频击穿强度测试

按照GB/T 3333—1999测定绝缘纸的工频击穿强度。具体为，采用不对称黄铜电极，表面均进行抛光处理，高压电极直径25 mm，低压电极直径75 mm；采用逐步均匀升压的方式进行测试，以测试数据的中位数作为最终实验结果。

1.5 GRA

GRA是一种基于灰色系统理论、定量描述和对比一个系统发展和变化的方法，是不确定系统研究领域的重要成果之一［15］。其基本思想是，将关注的研究对象及其影响因素看作一条曲线上的各点，参照曲线几何相似性，即形状越相似，两个变量之间的关联程度越高。通过计算多因素与同一参考序列之间的关联度，确定主导因素。该方法适用于解决多因素之间复杂的相互关系，其优点是不要求有大量的样本数据，也不要求样本数据有某种分布规律；具体过程如下［16］。

第一步，对获得的原始数据样本进行数据转换，使数据间可以进行比较。这是因为，各影响因素的物理意义不一样，为了确保构建模型的准确性，采用区间值化转换进行数据转换，分别对正、负序列采用下式处理。

第二步，确定绝对差序列：|x0（k）−xi（k）|。

第三步，根据式（3）计算灰色关联系数（GRC）。

通过比较GRG的大小来量化影响因素对指标的关联程度；GRG越高，则相关程度越高，影响程度越大。

2 结果与讨论

2.1 绝缘纸样品的各项参数

绝缘纸样品的纤维长度、纤维宽度、细小纤维含量、厚度、紧度、孔隙率和透气度7项参数测试结果如表2所示。为便于统计分析，将各参数映射到变量x1～x7。由表2可知，各项参数的变化幅度比较明显。

表2 纤维形态和纸张结构参数结果Table 2 Results of fiber morphology and paper structure parameters

绝缘纸的工频击穿强度数据如表3所示；其中，工频击穿强度（y）最大值为56.69 kV/mm，最小值为24.02 kV/mm，表明各绝缘纸样品间工频击穿强度差异明显。

表3 绝缘纸的工频击穿强度Table 3 AC breakdown strength of insulating paper samples

2.2 灰色关联分析

将工频击穿强度定义为参考序列，各参数定义为比较序列，按照式（1）～式（4）计算得到各影响因素的GRG，结果如表4所示。由表4可知，各参数对绝缘纸工频击穿强度的GRG在0.524～0.797之间；按GRG的大小排序为：纤维长度＞细小纤维含量＞纤维宽度＞紧度＞透气度＞孔隙率＞厚度。

表4 灰色关联度Table 4 Grey relational grades

图1为绝缘纸击穿的过程机理图，反映了击穿与电荷的关系［17］。由图1可知，绝缘纸的击穿往往是由内部纤维间孔隙的局部放电引起的，更小的孔隙可以承受更高的电场。较短的纤维可以改善纤维间的排列，减小孔隙；细小纤维也会填补在纤维间的孔隙中，影响孔径分布，从而降低绝缘纸的孔隙率；纤维宽度越小，紧度越大，纸张内部的纤维排列越紧密，孔隙越小。因此，纤维越短、细小纤维含量越高、纤维宽度越小、紧度越大，均有助于提高绝缘纸的工频击穿强度。此外，与添加纳米材料增强绝缘纸工频击穿强度的原理类似，细小纤维可以改善绝缘纸的表面均匀性，使绝缘纸表面电场均匀分布；同时增加绝缘纸内部的陷阱密度，可以限制载流子的运输，使得绝缘纸内部电子的有效平均自由行程变短，电子传输时不容易在电场中移动，并转变为速度较慢的电子，从而减轻对纤维素分子链的轰击，降低电离的概率，使得放电通道难以形成，在一定程度上抑制绝缘纸内部放电，从而提高绝缘纸的工频击穿强度［18-21］。

图1 绝缘纸击穿机理Fig.1 Breakdown mechanism of insulating paper

2.3 预测模型的建立

2.3.1 小样本和多重共线性问题

多元统计分析对自变量和测试样本的数量有要求，一般来说，构建多元回归模型所需的样本数量通常为自变量数量的2～5倍［4］。本课题研究中自变量有7个，而用来建立模型的模拟样本数量只有12个。因此，需要解决样本数量少的问题。

在考虑多个自变量进行研究时，当各变量之间存在较强的关系时，进行多元回归分析时经常产生多重共线性问题，导致不符合多元线性回归数学模型的基本假设。多重共线性会使模型的回归系数失去实际意义，其正负号也可能出现倒置。皮尔逊相关系数适用于表示两变量之间的相关性，其可量化不同变量之间的关联程度。一般认为，|r|≥0.8时，两变量高度相关；0.5≤|r|＜0.8时，两变量中度相关；0.3≤|r|＜0.5，两变量低度相关；|r|＜0.3，两变量不相关［22］。本课题中，自变量与因变量（共8个变量）的皮尔逊相关系数和双尾显著性概率以及变量之间的散点图和置信椭圆，如图2所示。散点图和置信椭圆可以直观地显示变量之间的关联程度。从图2可以看出，纤维宽度、细小纤维含量和紧度与绝缘纸工频击穿强度呈正相关关系；纤维长度、孔隙率和透气度与绝缘纸工频击穿强度呈负相关关系。各参数与绝缘纸工频击穿强度的皮尔逊相关系数基本大于0.5，说明它们之间具有很强的线性相关性；同样，部分变量之间存在很强的相关性，如细小纤维含量与纤维宽度、纤维长度和透气度之间。由此推断，可以使用多元线性回归进行绝缘纸工频击穿强度影响因素的分析，但各变量之间存在严重的多重共线性问题，将所有参数作为自变量直接进行回归，建立的回归方程模型是不合适的。

针对小样本和多重共线性问题，一方面可以增加样本数量，但增加样本数量有时是不现实的，如很多自变量不能控制，或者由于实际因素无法再获得一些样本数据；在一些情况下，当自变量的个数较多时，在选择增加样本数量的情况下，增加什么样的数据才能避免多重共线性问题是无法确定的。另一方面可以降低自变量的数量，可以剔除解释意义不强的自变量，直接选择解释意义非常强的自变量；还可以根据变量间的相关性对自变量进行重新组合，提取较少的变量。

考虑到增加测试样本的数量受到许多实际条件的限制，本课题选择减少变量的数量，即从7个参数中选择2～4个变量。主成分分析（PCA）适用于变量之间存在严重共线性的情况，在确保数据信息丢失最少的情况下，把多个变量转化为更少的几个新变量，是一种对多个变量进行降维的统计处理方法［22］。提取的新成分是原始多个变量数据的线性组合，它们之间无相关性，可以有效地代表原变量，从而简化复杂问题。最佳子集选择法是基于枚举的思想，对于给定数量的自变量遍历所有可能的组合，并列出变量子集中具有最高拟合度的子集；然后根据变量组合的R2和误差平方和（Mallows＇Cp）值选定参数的个数，可以确定适于多元线性回归建模的参数集［4］。本课题选择PCA和最优子集选择方法进行变量的选择，然后进行多元线性建模。

2.3.2 PCA的多元线性回归模型

在进行计算前，需对所有变量进行标准化变化，然后利用标准化变化的结果求解主成分会更加简便，标准化公式如下［22］。

图2 变量的皮尔逊相关系数Fig.2 Pearson correlation coefficients among variables

样本的充分性Kaiser-Meyer-Olkin（KMO）检测是检验变量之间偏相关的大小，它的取值范围在0～1之间，数值越大越适合进行PCA，小于0.5则不适合进行PCA；巴特利特球形度检验用于验证相关系数矩阵是不是单位矩阵，表明是不是适合进行PCA［23-24］。KMO检测和巴特利特球形度检验的结果如表5所示。由表5可知，本课题样本的KMO值为0.718，巴特利特球形度检验的显著性概率是0，说明变量间存在相关关系，可以进行PCA。

PCA方法的目的是用最少的主成分来表示原始变量最多的信息，可以根据主成分的累积贡献率和特征根来确定主成分个数。一般来说，累积贡献率达到80%以上就为满意；特征根是各个主成分影响大小的参数，一般保留特征根大于1所对应的主成分［22］。本课题研究中，7个自变量的主成分的特征根和累积贡献率如表6所示。由表6可知，第一、第二和第三主成分的特征根都大于1，同时，这3个主成分的累积贡献率为95.76%，所以，可选择提取这3个变量进行PCA。

表5 KMO检验和巴特利特球形度检验Table 5 KMO and Bartlett’s tests

表6 主成分的特征根和方差贡献率Table 6 Eigenvalues and its total variance explained

主成分的因子载荷反映变量在主成分上的重要性，3个主成分的因子载荷如表7所示。由表7可知，纤维长度、纤维宽度、细小纤维含量、紧度和透气度在第一主成分占较高的载荷，孔隙率在第二主成分占较高的载荷，厚度在第三主成分占有较高的载荷。如此，原来的7项参数转变为3个新变量，而这3个新变量能够解释原参数95.76%的信息。

表7 主成分的因子载荷Table 7 Component matrix of principal components

进行多元线性回归分析，建立标准化的因变量绝缘纸工频击穿强度（zy）与主成分F1、F2、F3的回归方程，如式（8）所示。

此模型的拟合度R2为0.917，说明模型具有较好的模拟性。为了进一步说明模型的合理性，图3给出了PCA回归模型标准化残差的结果。由图3可知，PCA回归模型标准化残差的正态P-P图呈近似线性趋势，表明残差服从正态分布，说明回归方程有效。对上述所求得的回归模型进行显著性检验，即方差分析。方差分析是对模型中多个自变量与因变量之间的线性关系在总体上是不是显著作出判断。方差分析结果表明，F=29.434，P=0＜0.05，说明通过检验，多元回归模型有意义。

图3 PCA回归模型标准化残差的正态P-P图Fig.3 The normal P-P plot of standardized residuals of the PCA regression model

通过转化，最终可得各参数与绝缘纸工频击穿强度的多元回归模型，如式（9）所示。

相对误差是指误差在真实结果中所占的比例，这对于比较在各种情况下所得结果的准确性更为方便。PCA回归模型预测值与实测值（见表3）的对比结果如图4所示。由图4可知，除了样本3号和7号的相对偏差为13.65%和11.84%，其余样本的相对偏差均在10%以内，说明该模型具有较好的模拟性。

为了对所得回归模型进行验证，需要制备验证样本以检验所构建模型的准确性。验证样本的各项参数如表8所示。将2组验证样本（13和14）数据代入上述回归模型中可得，两样本的工频击穿强度的预测值分别为44.83和30.65 kV/mm，与实测值（44.91和32.31 kV/mm）对比，计算所得偏差分别为−0.18%和−5.16%。可见，本课题建立的回归模型合理可信，具有良好的预测精度。

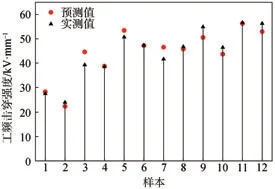
图4 PCA回归模型预测值与实测值的对比Fig.4 Contrast between fitting values of PCA regression model and actual values

表8 验证样本参数Table 8 Parameters of verification samples

2.3.3 最佳子集选择法的多元线性回归模型

由于本课题所选择变量的期望数量为2～4，因此在进行最佳子集选择时，给定变量的范围为1～6。绝缘纸工频击穿强度的最佳子集选择结果如表9所示。由表9可知，通过比较不同变量数量的最佳子集可以看出，随着变量数量的增加，拟合度R2增大，说明回归模型的拟合效果得到改善；但是，当自变量数量达到一定值时，R2的增大非常有限。变量数量从1增加到3，R2增大了0.134；从3增加到4时，R2只增大了0.012。因此，当变量数量达到3时，继续增加变量数量并不会使R2值显著增大。

Mallows＇Cp描述了模型的偏差和准确性，可以帮助在多个回归模型中进行选择，只有当Mallows＇Cp值接近预测变量数量加上常量，模型预测精度才更准确［4］。由表9可知，当变量数量为3时，Mallows＇Cp值为6.1，接近于6，符合要求。综合考虑拟合度R2值和Mallows＇Cp值可知，适合建立绝缘纸工频击穿强度的最佳子集选择多元线性回归模型（以下简称最佳子集选择回归模型）的参数是3个变量，分别为细小纤维含量、厚度和孔隙率。

表9 最佳子集选择结果Table 9 Results for the best subset selection

对绝缘纸工频击穿强度与细小纤维含量、厚度和孔隙率进行多元线性回归，得到模型如式（10）所示。

表10是最佳子集选择回归模型的基本信息。由表10可知，回归模型拟合度R2达到0.943，说明模型具有较好的模拟性。回归系数显著性检验可反映自变量与因变量的线性关系是否显著，x3、x4和x6的P值均小于0.05，说明它们与工频击穿强度存在显著的线性关系；x3、x4和x6的VIF非常接近于1，表明变量之间不存在多重共线性问题，不会对回归模型产生严重影响。

表10 最佳子集选择回归模型Table 10 Regression model for the best subset selection

图5给出了最佳子集选择回归模型标准化残差的结果。由图5可知，最佳子集回归模型标准化残差的正态P-P图近似呈线性趋势，表明残差服从正态分布，说明建立的回归方程有效。方差分析结果表明，F=43.883，P=0＜0.05，说明通过检验，回归方程有意义。

最佳子集选择回归模型预测值与实测值（见表3）的对比结果如图6所示。由图6可知，预测值和实测值的最大偏差为9.55%，二者非常接近，说明该模型具有较好的模拟性。将两组验证样本数据代入模型中，其预测值分别为44.62和36.57 kV/mm，与实测值对比，计算所得偏差分别为−0.64%和13.19%。可见，本课题建立的最佳子集选择回归模型合理可信，具有良好的预测精度。

图5 最佳子集选择回归模型标准化残差的正态P-P图Fig.5 The normal P-P plot of standardized residuals of the best subset selection method regression model

图6 实测值与最佳子集选择回归模型预测值对比Fig.6 Contrast between actual values and fitting values of regression model based on best subset selection method

综上可知，PCA解决了建模过程中多重共线性的问题，既不丢失原始数据的主要信息，又容易抓住主要矛盾，若将所有变量纳入模型，模型变得较为复杂。最佳子集选择方法简单直观，所得模型有较高的拟合度，降低了模型的复杂程度。

3 结论

本课题提出一种基于灰色关联分析的绝缘纸工频击穿强度影响因素的量化分析模型，分别采用主成分分析和最佳子集选择方法进行多参数优化，构建绝缘纸工频击穿强度的多元线性回归模型，主要结论如下。

3.1 绝缘纸工频击穿强度影响因素的灰色关联排序为：纤维长度＞细小纤维含量＞纤维宽度＞紧度＞透气度＞孔隙率＞厚度。

3.2 由相关性分析得出，纤维宽度、细小纤维含量和紧度与绝缘纸工频击穿强度呈正相关；纤维长度、孔隙率和透气度与绝缘纸工频击穿强度呈负相关。

3.3 利用主成分分析和最佳子集选择方法构建绝缘纸工频击穿强度的多元线型回归模型，模型的R2分别为0.917和0.943，两种模型的拟合度均较高；两种模型中，模拟样本和验证样本预测结果的相对偏差基本在10%以内，说明两种模型均具有良好的预测能力。