课程思政背景下高职数学课程设计研究

■张丽清，刘秀芬，赵家才

（1.厦门南洋职业学院人文社科学院，福建 厦门 361012；2.厦门软件学院，福建 厦门 361012）

2020年5月28日，教育部下发《高等学校课程思政建设指导纲要》，指导具体、要求明确、督促严厉。高校教育教学进行课程思政已成为刚需，课程建设融入课程思政，教学渗透课程思政的必要性是毋庸置疑的。目前“课程思政”的研究成为热潮。2019年至今关于“课程思政”的研究文献数量较之前明显增多，其中在中国知网中以“课程思政数学”作为主题查询，2018年约10篇，2019年约110篇，2020年至今约300篇。可见，数学课程思政研究渐渐进入白热化阶段。文献表明，目前高校数学课程思政的研究以课程思政探索与实践方向为主，如冯卫兵（2020）和杨 威（2020）、李洁坤（2019）等，都论证了大学数学课程开展课程思政的意义或必要性，提出了课程思政建设思路或策略与具体实践中的部分案例，期望“在整个数学教学系统中整理出一套可行、可操作、可借鉴的理论和课件，而不是像以前简单的碎片式的个例教育”[1]。部分学者更注重课程思政内涵分析，落脚点更细小，试图令数学课程思政建设理论更清晰、更可靠，如李万军（2020）的《课程思政理念下数学教育目标解析》、褚小婧（2020）的《大学数学课程思政内涵、内容选择与呈现方式》、胡先福（2020）的《高等数学课程思政的有效性与实践路径》等。而在“课程思政”背景下的数学课程建设、课程设计方案、思政资源开发等方面的研究较少，并且高校中高职的相应研究更为薄弱，研究空间尚在。

一、课程思政背景下高职数学课程设计的基本思路

高职数学课程一般包括高等数学（微积分为主）和工程数学（线性代数和概率论与数理统计为主）两门。数学课程一般在大一上学期或下学期开设，学时较少，教授内容有限。但高职数学教育教学依然身负重任，不仅要传授学生知识和培养学生能力，也要加强学生的情操陶冶、思想淬炼、价值塑造。数学教育要结合课程思政，将价值观渗透在数学课程教学的全过程，最终实现立德树人、全面育人的目的。

数学教师靠自身力量可能对“课程思政”的内涵和外延把握不够深入，但可以借思政教师的力量，研读领会党的各项方针政策、唯物辩证法思想、社会主义核心价值观等，以达到理解应用层次。在此基础上，挖掘思政元素，搜集并积累思政案例，群策群力发挥集体智慧是第一步；精心的课程设计，包括教学设计是第二步，只有教学设计精益求精，教师在教学中才能收放自如，有的放矢，避免随意发挥，词不达意，观点偏差。在课程思政背景下，笔者将从教学理念与教学模式、教学目标、教学内容三方面展开数学课程设计的研究。

二、课程思政背景下数学课程的教学理念与教学模式

数学课程作为高职理工科专业的基础必修课程，应根据学生特点和专业需求、学生发展需求三维度对学生进行因材施教，耐心引导，客观评价。高职数学有高等级、简洁抽象、逻辑强、符号化、理性等特征，所以学习起来需要有一定智力，需要有初等数学基础，需要脚踏实地、专注，需要日积月累持之以恒。这些对于高职生来说并不容易。面对高职生，比起一本正经、专心致志地传授数学知识，数学教育教学更应该注意感化教育的作用，这正是数学课程思政的部分。课程思政不仅不会增加教师负担，还能让学生在各种体验中得到洗礼，较好地提升教学效果。思政育人在当下相当重要。教育者须为学生的可持续发展考虑，依然应该注重知识传授和能力培养，与此同时，应在价值引领与品格塑造上下足功夫。所以现在数学课程采用“知识+能力+价值”的教学模式。

三、课程思政背景下数学课程的教学目标

在课程思政理念下，学者李万军将数学教育目标分成三个层次：知识性目标、能力性目标、思想性目标。三个层次由浅入深，呈递进关系。知识性目标是基础，能力性目标是核心，思想性目标是发展和升华，每一层次目标的实现，都是数学教育的一种更高境界[2]。每一层次又细分为三个阶段。知识性目标包括生活必需的数学知识（基础性阶段）、个人发展所必需的实用性数学知识（实用性阶段）、数学知识的内涵（领悟性阶段）三个阶段；能力性目标包括数学基础能力、数学核心能力、数学应用能力三个阶段；思想性目标包括情感态度层次、德育层次、哲学层次三个阶段。

借鉴以上数学教育目标理论，高职数学课程目标可分为三个层次：知识目标、能力目标、思想目标。知识目标：使学生获得进入社会所必需的数学知识与后续发展所需要的较高水平的数学准备；能力目标：使学生获得观察力、数学言语表达能力、推理能力等基本数学能力，并提高数学运算能力、逻辑思维能力和空间想象能力三大核心能力，以及形成数学思维应用意识，提高数学应用能力；思想目标：使学生积极参与数学学习活动、数学体验活动，体验数学与日常生活的密切关系，以及对生活或其他学科的促进作用，感受数学的应用价值，学会欣赏数学之美，探索数学中的奥秘，形成独立思考的习惯、实事求是的态度；通过数学史、数学家故事等人文素材使学生领会其中深层涵义，强化意志力与道德行为等，树立正确的人生观、价值观、世界观。

四、课程思政背景下数学课程的教学内容

（一）数学课程的具体教学内容

数学课程（下文均指高等数学课程）的主要教学内容为微积分，一般包含极限、导数与微分、不定积分与定积分、微分方程等。由于总课时64学时与学生水平的限制，具体教学内容的选择与教学深度的把握都存在难度，目前教研室教师的做法是以专业需求为先，确定教学内容大方向；采用诊断性评价对学生水平进行摸底，寻找学生的“最近发展区”，进而确定具体教学章节与教授深度；再利用形成性评价来进行班级微调教学内容。这样做可行，但这样远远不够，教学效果不会因此就大幅提升。教学内容的合理选择是有效教学的必要保障。而学生是学习的主体，他们的学习主动性、积极性是提升学习成效的关键。所以教师需要耐心地引导学生，感化学生；学生需要感受到数学文化与数学价值，体验到学习数学的乐趣或意义。数学课程思政必须有机融入数学教学内容中，丰富学生的学识与思想，对学生起价值引领与品格塑造作用。

数学课程为专业学习提供数学基础，于是教学主要内容大方向不能变；学生基础不仅差异大，也存在普遍水平偏低、个别基础较好的现象。教师必须懂得取舍，先抓基础，讲得多并不一定好，比如两个重要极限、隐函数求导、拉格朗日中值定理、技巧计算（难度计算）、可降阶的高阶微分方程等根据学生课堂具体情况再定夺取舍。个别基础好的学生可以区别加料。最终确定数学课程的基础版的具体教学内容，每个章节后的括号内所列为授课内容范围见附表1。

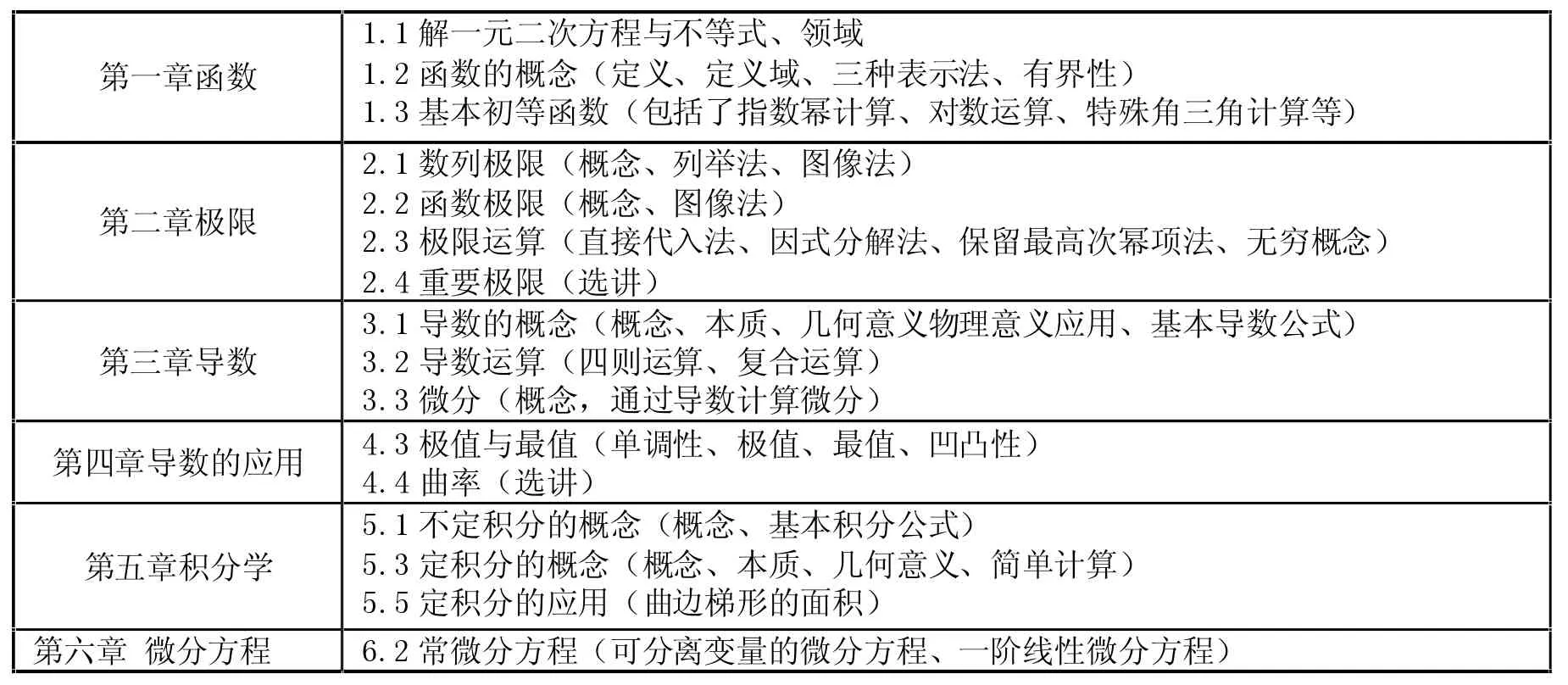
附表1 数学课程的具体教学内容

（二）数学课程思政的构想

《高等学校课程思政建设指导纲要》指出“课程思政的内容要……围绕政治认同、家国情怀、文化素养、宪法法治意识、道德修养等重点优化课程思政内容供给，系统进行中国特色社会主义和中国梦教育、社会主义核心价值观教育、法治教育、劳动教育、心理健康教育、中华优秀传统文化教育。”那么数学课程以微积分为主要内容，蕴含着丰富的以辩证唯物主义思想为主的哲学思想、数学思想、数学文化，及与现实生活紧密联系的案例、人生道理哲理等。教师应着重从教材分析，把握内容思政的时机和方式，以免牵强附会、生搬硬套起到反效果。“大学数学课程思政不能改变原有的以知识逻辑和心理逻辑为基础编制的内容和顺序，只能选择合适的数学课程内容并潜在地进行价值观的渗透”[3]。探索数学课程思政的部分构想见附表2。

附表2 数学课程思政的部分构想

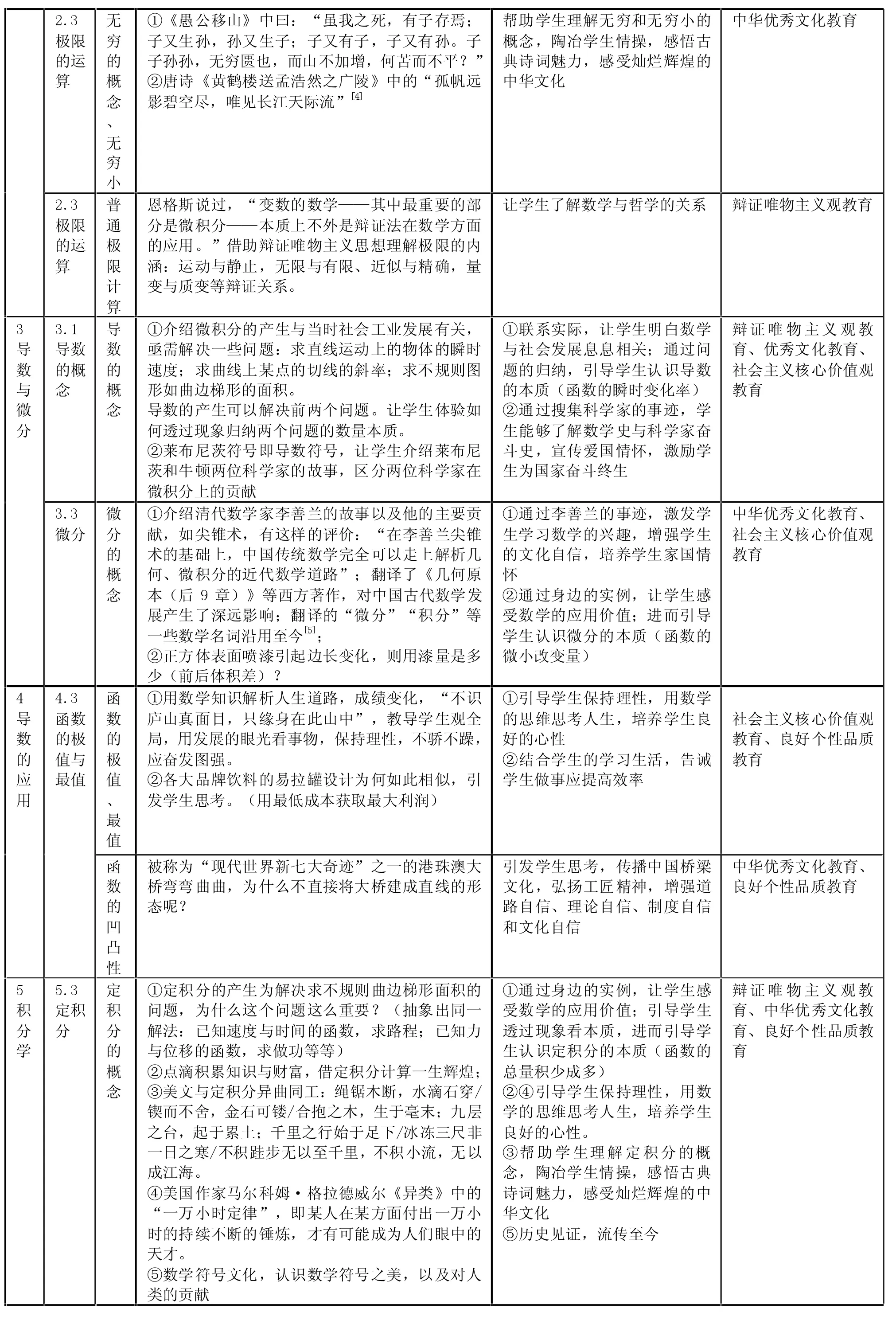
2.3极限的运算无穷的概念、无穷小①《愚公移山》中曰:“虽我之死,有子存焉;子又生孙,孙又生子;子又有子,子又有孙。子子孙孙,无穷匮也,而山不加增,何苦而不平?”②唐诗《黄鹤楼送孟浩然之广陵》中的“孤帆匹影碧空尽,唯见长江天际流”images/BZ_166_1035_424_2084_443.pngimages/BZ_166_1044_424_2093_443.pngimages/BZ_166_1054_424_2103_443.png帮助学生理解无穷和无穷小的概念,陶冶学生情操,感悟古典诗词魅力,感受灿烂辉煌的中华文化中华优秀文化教育2.3极限的运算普通极限计算恩格斯说过,“变数的数学——其中最重要的部分是微积分——本质上不外是辩证法在数学方面的应用。”借助辩证唯物主义思想理解极限的内涵:运动与静止,无限与有限、近似与精确,量变与质变等辩证关系。让学生了解数学与哲学的关系 辩证唯物主义观教育3导数与微分3.1导数的概念导数的概念①介绍微积分的产生与当时社会工业发展有关,亚需解决一些问题:求直线运动上的物体的瞬时速度;求曲线上某点的切线的斜率;求不规则图形如曲边梯形的面积。导数的产生可以解决前两个问题。让学生体验如何透过现象归纳两个问题的数量本质。②莱布尼茨符号即导数符号,让学生介绍莱布尼茨和牛顿两位科学家的故事,区分两位科学家在微积分上的贡献①联系实际,让学生明白数学与社会发展息息相关;通过问题的归纳,引导学生认识导数的本质(函数的瞬时变化率)②通过搜集科学家的事迹,学生能够了解数学史与科学家奋斗史,宣传爱国情怀,激励学生为国家奋斗终生辩证唯物主义观教育、优秀文化教育、社会主义核心价值观教育3.3微分微分的概念①介绍清代数学家李善兰的故事以及他的主要贡献,如尖锥术,有这样的评价:“在李善兰尖锥术的基础上,中国传统数学完全可以走上解析几何、微积分的近代数学道路”;翻译了《几何原本(后 9章)》等西方著作,对中国古代数学发展产生了深匹影响;翻译的“微分”“积分”等一些数学名词沿用至今images/BZ_166_929_1628_1978_1647.pngimages/BZ_166_938_1628_1987_1647.pngimages/BZ_166_948_1628_1997_1647.png;②正方体表面喷漆引起边长变化,则用漆量是多少(前后体积差)?①通过李善兰的事迹,激发学生学习数学的兴趣,增强学生的文化自信,培养学生家国情怀②通过身边的实例,让学生感受数学的应用价值;进而引导学生认识微分的本质(函数的微小改变量)中华优秀文化教育、社会主义核心价值观教育4导数的应用4.3函数的极值与最值函数的极值、最值①用数学知识解析人生道路,成绩变化,“不识庐山真面目,只缘身在此山中”,教导学生观全局,用发展的眼光看事物,保持理性,不骄不躁,应奋发图强。②各大品牌饮料的易拉罐设计为何如此相似,引发学生思考。(用最低成本获取最大利润)①引导学生保持理性,用数学的思维思考人生,培养学生良好的心性②结合学生的学习生活,告诫学生做事应提高效率社会主义核心价值观教育、良好个性品质教育函数的凹凸性被称为“现代世界新七大奇迹”之一的港珠澳大桥弯弯曲曲,为什么不直接将大桥建成直线的形态呢?引发学生思考,传播中国桥梁文化,弘扬工匠精神,增强道路自信、理论自信、制度自信和文化自信中华优秀文化教育、良好个性品质教育5积分学5.3定积分定积分的概念①定积分的产生为解决求不规则曲边梯形面积的问题,为什么这个问题这么重要?(抽象出同一解法:己知速度与时间的函数,求路程;己知力与位移的函数,求做功等等)②点滴积累知识与财富,借定积分计算一生辉煌;③美文与定积分异曲同工:绳锯木断,水滴石穿/锲而不舍,金石可镂/合抱之木,生于毫末;九层之台,起于累土;千里之行始于足下/冰冻三尺非一日之寒/不积趾步无以至千里,不积小流,无以成江海。④美国作家马尔科姆·格拉德威尔《异类》中的“一万小时定律”,即某人在某方面付出一万小时的持续不断的锤炼,才有可能成为人们眼中的天才。⑤数学符号文化,认识数学符号之美,以及对人类的贡献①通过身边的实例,让学生感受数学的应用价值;引导学生透过现象看本质,进而引导学生认识定积分的本质(函数的总量积少成多)②④引导学生保持理性,用数学的思维思考人生,培养学生良好的心性。③帮助学生理解定积分的概念,陶冶学生情操,感悟古典诗词魅力,感受灿烂辉煌的中华文化⑤历史见证,流传至今辩证唯物主义观教育、中华优秀文化教育、良好个性品质教育

五、实践

近三年，笔者所在院校在全校推广课程思政。数学教研室在前期教学改革中吸取经验与教训，不断拓宽教学改革思路，认为数学课程思政是提升教学效果的良策之一。教研室提出数学课程思政的试行方案，引导组内教师进入“学习-交流-实践”的循环模式，不断完善课程设计方案，即定期定量完成文献阅读，定期交流总结并用于教学实践，建设数学课程的思政资源库，更新数学课程设计方案。课程思政理论在教学实践中初见效果，课堂听课率有所上升，学生参与度提高等，但在教学典型案例库的建设上仍需努力。总之，数学课程思政的工作需要群策群力，多方协作，密切配合，做到尽善尽美。