小学数学典型错例分析及矫正策略

○刘爱东

数与代数

【错例】

计算下面各题，能简算的要简算。

正确答案：

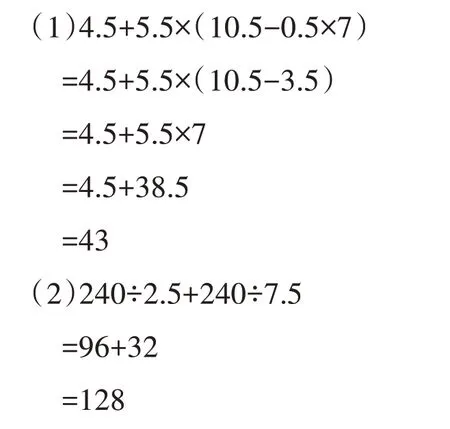
【诊断】

1.信息负迁移干扰思维。

运用凑整进行简便计算的关键是数、运算符号及运算顺序相配合，三者缺一不可。受“能简算的要简算”的要求影响，第（1）小题，学生过度关注了数、运算符号能否凑整，而忽略了运算顺序是否正确；第（2）小题，把乘法分配律错误地运用到了除法计算中。

2.缺乏正确审题的意识。

学生良好的审题习惯还没有真正养成，书写之前，没有做到仔细观察、厘清运算顺序，而是凭经验、根据数据凑整做题。同时，学生对算理还没有真正理解和掌握，导致审题时抓错“关键点”。

【对策】

1.经历算理算法提炼过程，培养良好习惯。

教师要注重引导学生经历计算方法的形成过程，深入分析内在道理，引导学生多问几个“为什么”。只有在算理算法的指导下，厘清运算顺序，才能根据数和运算符号的特点，确定是否可以进行简便计算，为培养良好的审题习惯打下基础。

2.注重培养整体建构意识，加强题组辨析。

教学中，教师要注重引导学生经历细心审题、书写步骤、检验结果的完整过程。要让学生把整个的思考过程，都在简便计算的过程中呈现出来。要精心设计题组练习，并揭示可能的解题错误，引导学生融错学习，积累经验，使错例成为学生正确计算的宝贵资源。

3.加强简便计算应用练习，培养数学素养。

对于明确要求简便计算的习题，学生大都能简便计算，而对于没有明确要求但内含简便计算的习题，学生常常不敢使用或忽略了。不妨引导学生多关注生活中简便计算应用的简洁性，促进学生主动应用简算方法，解决实际问题。

【练习】

计算下面各题，能简算的要简算。

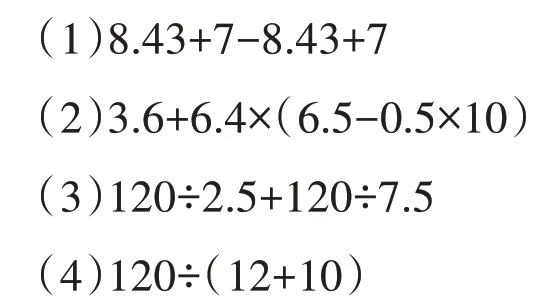
【错例】

计算下面各题，能简算的要简算。

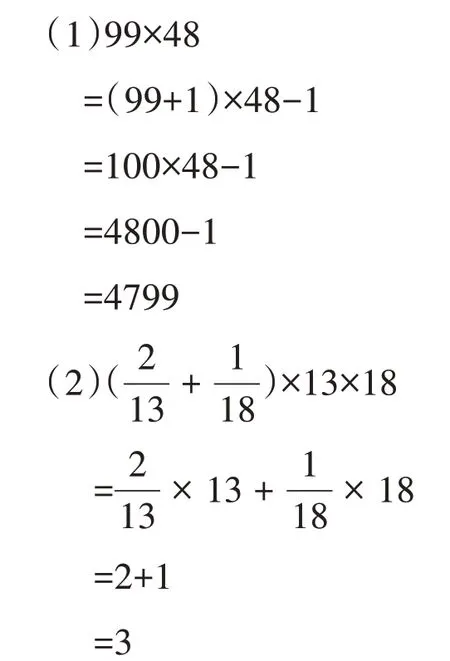
正确答案：

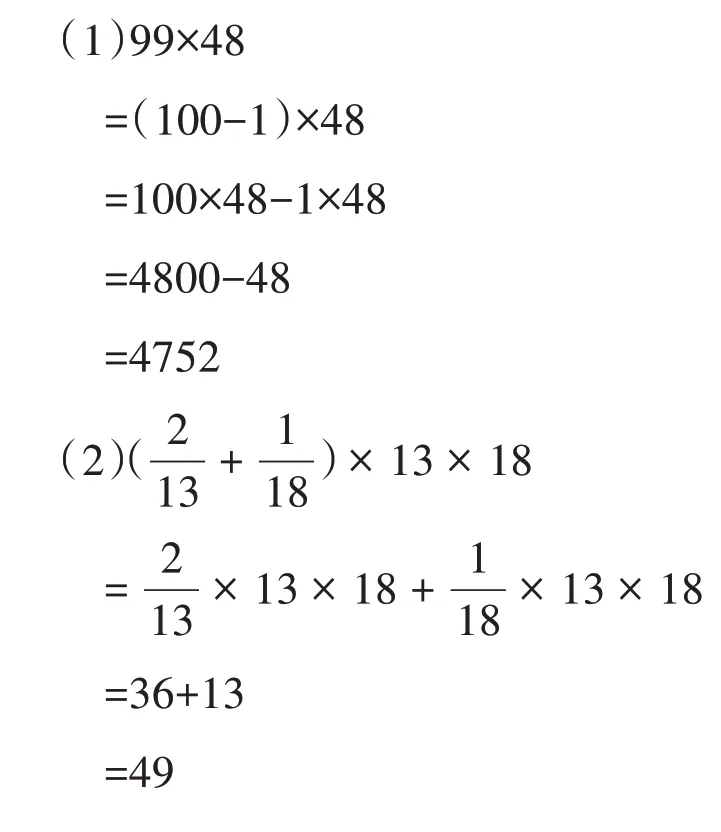
【诊断】

1.对运算律的错误表征与解读。

从解题过程来看，学生有应用运算律进行简便计算的意识，但由于对运算律和运算性质的理解只停留在表面，缺乏实质性把握，导致实际计算时不能灵活应用，产生错误。

2.缺乏对计算结果合理性的判断。

受计算速度要快的内在心理影响，学生简便计算时，通常缺少对计算结果合理性进行判断这一步，导致对明显的错误结果“视而不见”。比如通过估算，可以判断计算的结果是否合理。第（1）题，通过口算两个乘数个位上数相乘的积9×8=72，可以确定原式积的个位一定是2，由此判断结果4799 一定是错误的。

【对策】

1.重视运算律的多元表征与解读。

教学时，一方面，要引导学生根据运算意义选择合适的方法；另一方面，则要启发学生联系现实背景，多角度解释简便计算的过程。比如，99×48，可以表示求99 个48 相加的和是多少，而99 个48 等于100 个48 减去1 个48，所以99×48=100×48-1×48；也可以创设购物情境：“每个书包48 元，买99 个书包一共需要多少元？”可以先算100 个书包的价钱，再从中减去一个书包的价钱，即99×48=100×48-1×48。

2.加强计算结果合理性的判断。

教师要舍得花时间，培养学生做题前认真审题、合理选择方法、规划计算过程，做题后主动反思、多角度判断计算结果合理性的良好习惯，逐步提高计算的正确率。

【练习】

计算下面各题，能简算的要简算。

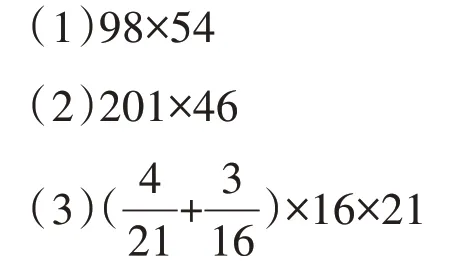
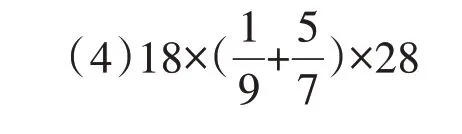
【错例】

A.两条一样长 B.第一条长

C.第二条长 D.无法比较

正确答案：

D

【诊断】

1.具体数量与分率区分不清。

学生对于分数的两种表示方式的理解比较模糊，没有真正理解“分数既可以表示一个具体的数量,也可以表示两个数量之间的倍数关系（分率）；当表示具体的数量时带单位，表示分率时不带单位”。只是根据题中两个分数相同，而误以为用去的长度相等。

2.考虑问题不全面。

受“两条同样长的彩带”这一信息干扰，学生以为既然同样长，表示用去的分数也一样多，所以剩下的也同样多，却没有考虑到彩带的长度有大于1 米、等于1 米和小于1 米三种情况。

【对策】

1.注重分数意义的建构。

学习分数意义时，教材通常从表示具体数量的分数出发，引出表示分率的分数，如从个蛋糕出发，引出半个蛋糕是一个蛋糕的。教师要有意识地引导学生结合生活实际，正确区分表示具体数量的分数与表示分率的分数。

2.引导学生考虑问题要周全。

教师要引导学生在解决问题时，把各种可能的情况都考虑进去。例题中两条同样长的彩带的长度一共有三种情况，当彩带的长等于1米时，第一条用去的就是米，跟第二条一样多，所以剩下的也一样长；当彩带的长大于1米时，第一条用去的就大于米，所以第二条剩下的长；当彩带的长小于1米时，第一条用去的就小于米，所以第一条剩下的长。综上所述，三种情况都有可能，所以选D。

【练习】

A.一样长 B.第一根长

C.第二根长 D.无法比较

A.一样长 B.第一段长

C.第二段长 D.无法比较

A.甲绳长 B.乙绳长

C.一样长 D.无法比较

【错例】

正确答案：

2

【诊断】

1.解题思维能力偏弱。

题目涉及分数除法、乘法分配律、用字母表示数的计算等知识。思维能力偏弱的学生，习惯于整数的运算，对于分数且含有字母的计算，往往不知道从哪儿下手。看到式子比较复杂，又含有字母a 就慌了，计算时不论写到哪个数，都想着后面要写上字母a。

2.解题策略储备单一。

由于思维力较弱，所以遇到熟悉的、思维含量比较少的问题时，学生能够依样画葫芦去解决，但遇到不熟悉的、思维含量比较多的题目时，往往局限于某一种思路而不能自拔。比如，出错的学生通常陷于“怎样处理字母a”“数与字母不能直接计算怎么办”的纠结中，而没有思考是否还有其他的解决方法。

【对策】

1.注重数学知识的形成过程。

再复杂的计算都是以简单的计算为基础的，因此，要通过数形结合、动手操作、推理验证等多种方法，引导学生在经历探究、创新知识的过程中，获得方法、理解概念、发展思维，积累解决复杂问题的思想、策略和方法。

2.注重数学思维的培养提升。

教学中，教师要创设探索、思考的情境，引导学生经历思维顿悟、体验成功的快乐。比如，可以提出“怎样利用乘法分配律改写去掉小括号后的算式是怎样的”“比较两个算式，你有什么发现”等问题，引导学生的思维不断深入。

3.注重问题解决策略的培养。

引导学生不能只满足于会用一种方法解决问题，而应多想一想“还有没有其他的解决方法”。这样，在遇到新的问题时，学生才会从多个角度去尝试解决。比如，这道题还可以用假设法来解决，把字母a 用一个具体的数来代替。假设a是，则，去掉小括号后的式子进行计算，，所以4-2=2。

【练习】

2. 4（x+5）比4x+6（ ）（填“多”或“少”）了（ ）。

【错例】

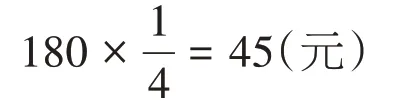
答：现价比原价便宜了45 元。

正确答案：

解：设这种商品的原价是x 元。

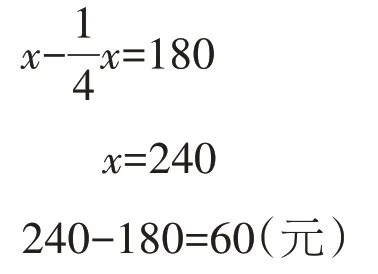
答：现价比原价便宜了60 元。

【诊断】

1.缺少对数量关系的深入分析，没有找准单位“1”。

2.没有理解分数的意义，思考问题简单。

“现价比原价便宜45 元”就是“原价比现价贵45 元”，受此影响，学生以为“现价比原价便宜”也就是“原价比现价贵，把单位“1”人为地进行了简单化处理，没有真正理解分数的意义。

【对策】

1.理解分数意义，厘清量率关系。

这是“求一个数比另一个数多（少）几分之几”的实际问题，难在如何正确理解“比原价便宜了”。教师可以从两方面进行引导：一要明确是哪两个部分相比，把省略式句子补充完整，即“（现价）比原价便宜了”，是“便宜的部分”跟“原价”比；二要确定谁是单位“1”的量，根据两个部分比较的情况，可以知道“原价”是标准量，因此要把原价看作单位“1”。

2.抓住问题本质，分析数量关系。

“现价”是已知的，“原价”和“现价比原价便宜多少”都是未知的，但“现价比原价便宜多少”可以用单位“1”的量（即原价）的式子来表示。单位“1”的量未知，可以用方程或除法来求。

3.重视数形结合，善于化难为易。

“求一个数比另一个数多（少）几分之几”的实际问题，数量关系相对比较复杂，涉及两个量的双重比较，既有差比，也有倍比。如果我们引导学生用数形结合的思想方法分析，如画线段图，哪个量多哪个量少，以及相互间的关系，就会一目了然，可以用更加简便的、份数的方法180÷3×1=60（元）来求。

【练习】

1.一种商品现在售价150 元，比原价降低了50 元，比原价降低了几分之几？

【错例】

李叔叔的打字速度是70 字/分，如果他每打30 分钟休息5 分钟。那么从上午7 时到9 时，李叔叔一共打了多少字？

错解一：

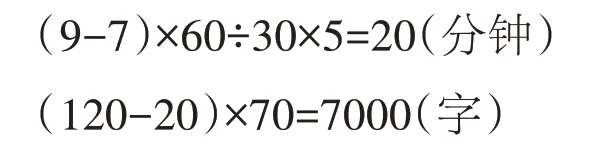
答：李叔叔一共打了7000 字。

错解二：

答：李叔叔一共打了6300 字。

正确答案：

答：李叔叔一共打了7350 字。

【诊断】

1.关键信息理解不到位。

题中数量关系比较复杂，解题的关键是正确理解“每打30 分钟休息5 分钟”这一条件的意思，并能用自己的方法整理和分析数量关系。错解一把条件“每打30 分钟休息5 分钟”中的“休息5 分钟”，误以为是包括在30 分钟里面的。

2.数量关系分析不精准。

有的学生虽然能理解“每打30 分钟休息5 分钟”的含义，能把30 分钟与5 分钟之和看作一个整体进行计算，但并没有把最后一段不足30 分钟的打字时间计入总打字时间，说明学生未能正确分析打字时间与休息时间的关系。

3.解决问题策略不丰富。

凡使用画图、列表等比较直观的方式，帮助整理条件并解决问题的学生，正确率通常比较高。说明数形结合的方法，能够有效减轻学生思维的负担，帮助学生较为轻松地解决抽象的问题，而仅仅想到列式这一种策略的学生，一旦思维受阻就束手无策了。

【对策】

1.加强关键信息的针对性训练。

有的条件中蕴含着关键信息，学生往往因为缺少数学经验而抓不住它，或者找到了关键信息，但并没有真正理解其含义，导致做题时出现错误。教师在日常教学中要做有心人，主动收集容易发生歧义或不好理解的信息，组织学生开展针对性训练，使学生会寻找并理解关键信息。

2.运用多种策略外显数量关系。

数学本身以严谨著称，解决问题中一般不会出现模棱两可、似是而非的条件或问题，要引导学生抓住数学的本质，采用画图分析、列表整理等方法，精准分析数量关系。数量关系弄清楚了，解决问题也就容易了。

【练习】

1.某工厂规定工人每上机工作60 分钟就要休息10 分钟。王叔叔从8 时上班到12 时下班。他一共上机工作多少分钟？

2.李阿姨的打字速度是80 字/分，每打30 分钟休息10 分钟。如果她从早晨7 时起，打印一份10000 字的报告，打印结束时是几时几分？

图形与几何

【错例】

把一张正方形的纸连续对折5 次，折后的每一小块占这张正方形纸的（）。

正确答案：

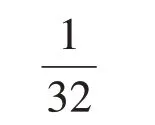
【诊断】

1.题意理解出现偏差。

学生知道“对折”是将纸平均分成两份，却错误地把“对折5 次”理解成是把纸平均分成5 个两份，而没有意识到每次对折都需要把前一次对折后的结果作为单位“1”再平均分。

2.动手操作意识淡薄。

如果学生能够养成动手操作的习惯和意识，根据题目中的条件，拿出一张纸动手折一折，并从中发现“每对折一次，所折成的份数都是原来的两倍”这一规律，答案就能轻松找到。这说明学生平时动手操作解决问题的意识和机会都比较少。

3.空间想象能力缺乏。

教学时，教师普遍会引导学生开展操作活动，学生也能根据操作结果，很快地得出正确结果。但由于很多教师只满足于结果的获得，而缺乏引导学生对结果的再认识、再思考，导致空间想象能力较弱。

【对策】

1.认真审题，正确理解题意。

只有认真审题、正确理解题意，才能为分析数量关系、解决问题提供基础和保障。教师要引导学生通过动手操作，真正理解“连续对折5 次”的含义,即把最初的那张正方形纸平均分成了2×2×2×2×2=32（块），则每一小块占这张正方形纸的。

2.注重过程，培养空间观念。

教师要引导学生经历对折正方形纸的过程，并在折的过程中，不断地比较、思考、描述，促进学生建构空间观念，并由关注折实物的过程，渐渐上升为对折后规律的思考。比如，引导学生思考：如果折的次数比较多，纸折不起来或不能折时，该怎么办？促进学生在找规律的基础上，运用规律解决问题。

【练习】

1.把一张长方形的纸连续对折4 次，折后的每一小块占这张长方形纸的（ ）。

2.将一张正方形的彩纸沿着同一个方向对折，对折4 次后有（ ）条折痕。

3.把一张正方形纸连续对折3 次后，每一小块的面积是3 平方厘米，则这张正方形纸原来的面积是（ ）平方厘米。

4.把一个圆形纸片对折3 次，得到一个扇形，量得扇形的弧长是6.28 分米。这个圆的半径是（ ）分米。

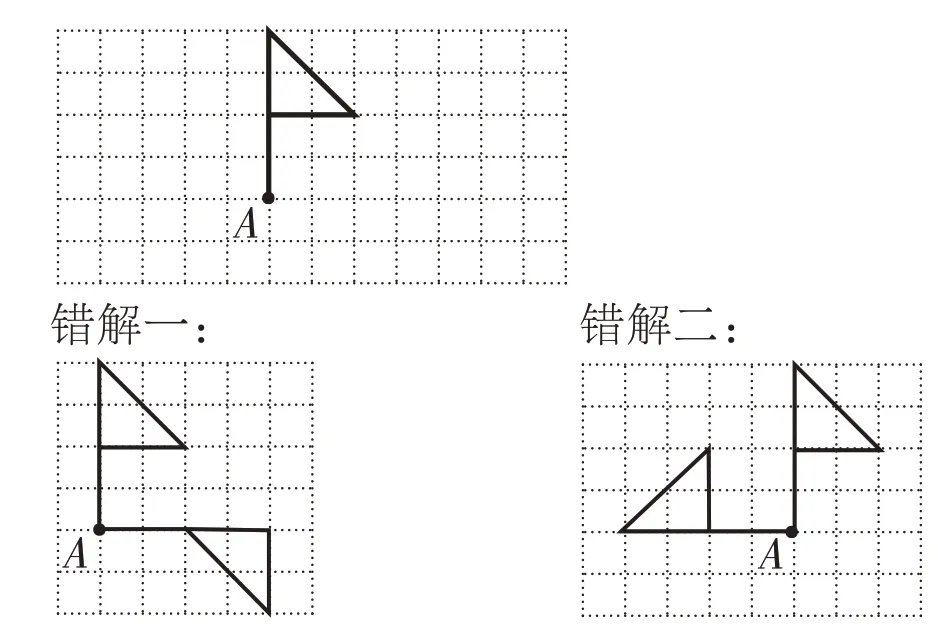
【错例】

把小旗图围绕A 点顺时针旋转90 度，请你画出旋转后的图形。

正确答案：

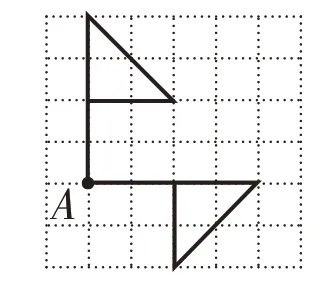
【诊断】

1.整体感知和描述能力不足。

由于受学习、生活经验不足的影响，学生空间观念相对薄弱，整体感知和描述图形的能力还比较欠缺。比如，左边那幅图，旋转的方向是对的，但所画小旗的整体形状却已经发生了变化。

2.受思维定势的负面影响。

有的学生习惯地认为，平移的方向不是从上往下，就是从左往右；旋转的方向都是顺时针方向。当遇到稍微复杂一些的图形运动的问题时，学生会受这种固有思维的影响，产生错误的判断。

【对策】

1.借助实物操作，在反复比较中完善认知。

引导学生在亲身经历图形旋转的过程中，掌握操作要领，把握操作规律，完善概念认知。教学中，可以先剪一个与小旗大小、形状都一样的实物图片，让学生按照要求在图上围绕指定的点转一转，重点引导学生关注旋转前后小旗的边或顶点发生的变化，体会图形旋转后位置发生了变化，但形状和大小是不变的。

2.注意逐步过渡，搭建合适的上升阶梯。

在经过实物操作、明晰旋转要素的基础上，引导学生由旋转简单图形逐步过渡到旋转稍复杂的图形。比如，指导学生先旋转线段，再旋转长方形、正方形，之后旋转三角形、梯形及不规则图形等。要引导学生说清楚“绕哪个点旋转”“按什么方向旋转”“旋转了多少度”等操作过程中的基本问题。还可以借助多媒体课件等直观手段，把旋转过程动态演示出来，也可以借助实物检验旋转结果是否正确。

【练习】

1.从3 时到6 时，时针绕中心点（ ）（填“顺”或“逆”）时针旋转了（ ）度。从6 时到12时，时针绕中心点（ ）（填“顺”或“逆”）时针旋转了（ ）度。

2.把三角形ABC 先向上平移3 格，再向左平移5 格，正好达到图中的位置。请你在图中画出三角形ABC 原来的位置。

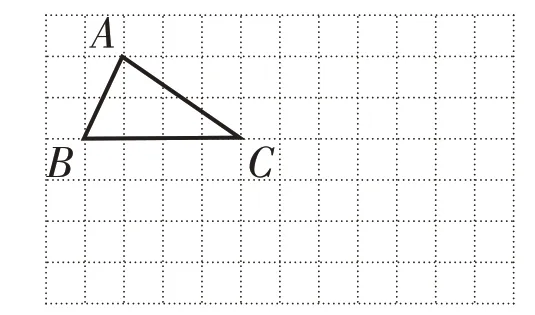
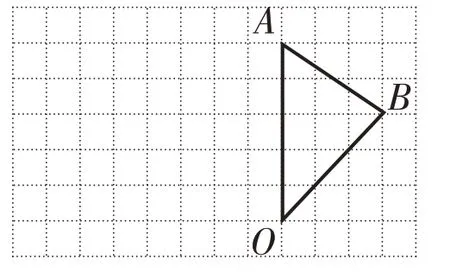
3.画出三角形AOB 绕O 点逆时针旋转90 度后得到的图形。

【错例】

求出下面图形的周长。

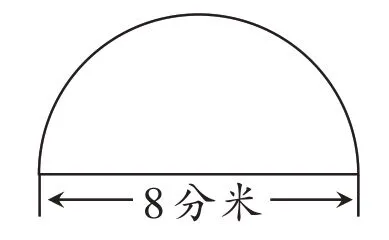
正确答案：

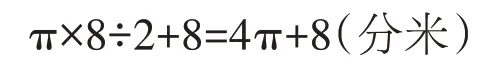
【诊断】

1.受直观感知的影响，周长与面积相混淆。

对于圆，学生最先感知的是整个圆的“面”，其次才是“线”，因此，容易受“半圆面积是半径相同的整圆面积的一半”的负迁移，产生“半圆周长是半径相同的整圆周长的一半”的错误结论，即用整圆的周长除以2 来求半圆的周长。

2.对周长概念理解不深，应对问题能力不足。

我们在学习圆的周长时，通过绕线法、作记号滚动法等，化曲为直测量圆的周长。当出现求半圆周长时，如果也能像初学圆的周长那样，先用直观的方法表示出半圆的周长，比如用笔把这个半圆的周长画出来，那么“半圆的周长由圆周长的一半与圆的直径两部分组成”就一目了然了。

【对策】

1.首次感知需建构正确的概念。

要使学生对圆的周长和面积不产生混淆，需要在他们首次接触周长、面积时，创设丰富的活动情境，让学生在指一指、摸一摸、描一描、画一画、剪一剪、量一量等过程中，充分感知周长与面积的含义，比较周长与面积的异同，建构正确的概念。

2.注重体验感悟中加强辨析。

由于错误出现在“半圆的周长”与“圆周长的一半”这两个相似内容上，因此有必要对所学内容适时开展比较、辨析的教学。比如，从概念的内涵进行梳理、比较，请学生动手指一指、描一描这个半圆的周长，说一说它与圆的周长相比有什么特殊的地方。从而使学生理解半圆的周长不是圆周长的一半，是由圆周长的一半和圆的一条直径组成的。

【练习】

1.把一个半径8 分米的圆，沿直径切成两半，所得到的图形跟原来的图形相比，周长（ ），面积（ ）。（括号里填“变了”或“不变”。）

2.求出下面图形的周长和面积。（单位：米）

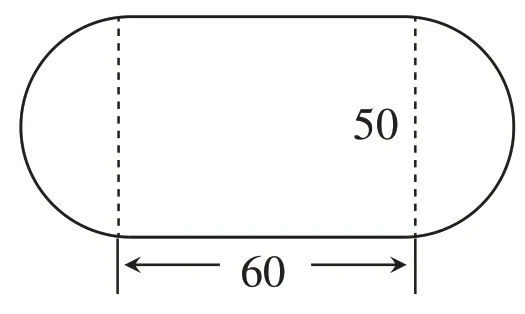
【错例】

在直径是8 米的圆形花坛外面，有一条宽2米的小路，这条小路的面积是多少平方米？

错解一：π×[（8+2）÷2]2-π×（8÷2）2=9π（平方米）

错解二：π×（8÷2）2-π×（2÷2）2=15π（平方米）

正确答案：

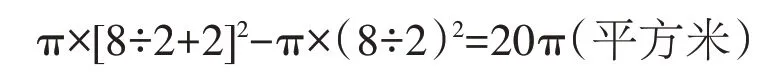
【诊断】

1.空间观念薄弱，处理复杂条件经验不足。

相对于长方形、正方形、圆的面积的计算，圆环面积的计算更加复杂，生活中，圆环的内容也比较少。考虑到实际情况，教材中涉及圆环面积的教学，通常都会配上示意图，并直接告知学生圆环外圆和内圆的半径（直径）的长度，学生只要抓住公式，处理起来并不很难。因此，学生往往会形成这样错误的想法，数值大的就是圆环的外圆半径（直径），数值小的就是圆环的内圆半径（直径）。

2.过度依赖直观，思维不够缜密。

正是因为教材中遇到圆环问题，一般都会配上相应的示意图，因此，学生对于直观产生了一定的依赖，习惯于从图中获取、分析信息，以至于离开了图，就不会分析“圆形花坛外面宽2 米的小路”，到底是花坛的半径多了2米，还是直径多了2米。

【对策】

1.丰富数学经验，培养空间观念。

如果没有现实生活中的亲身经历，学生学习数学的前置经验就会有缺失，遇到的数学问题即便来自于现实生活，也会无从入手。因此，可以组织学生走出教室，亲身参与观察、测量、交流等活动过程，让他们自主发现“宽2 米的小路”原来就是让花坛的半径多出2 米，或者是让花坛的直径多出两个2 米。

2.养成画图习惯，体验画图价值。

教学时，要引导学生善于将抽象的文字转化成具体的图形，通过画图表征题意，并把数据在图中标示，能够直观地看到各数量间的关系。比如，大圆的半径就是花坛的半径加上小路的宽度。画图的策略，也有利于排除无关因素的干扰，让学生将注意力聚焦于大圆和小圆的半径上。

3.适度拓展练习，优化数学思维。

圆环面积的计算有很多拓展的题型，比如，可以将圆环与正方形、三角形进行组合，求出指定部分的面积。教师要有意识地寻找符合学生认知特点的题目，指导学生在自主思考、互动交流中加强认识，促进几何直观思维的发展。

【练习】

1.在半径6 米的圆形花坛外，铺一条宽4 米的环形石子路。这条石子路的面积是多少平方米？

2.在直径6 米的圆形花坛外，铺一条宽4 米的环形石子路。这条石子路的面积是多少平方米？

3.在周长25.12米的圆形花坛外，铺一条宽4米的环形石子路。这条石子路的面积是多少平方米？

【错例】

李师傅剪出如图所示的一张长方形铁皮中的涂色部分，正好可以做成一个圆柱。做成的圆柱的体积是多少立方分米？

正确答案：

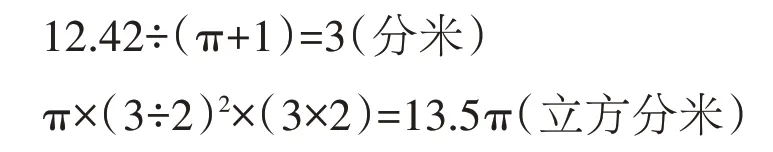
答：做成的圆柱的体积是13.5π 立方分米。

【诊断】

1.读图能力不足。

从错解可以看出，学生不善于从图中读出解决问题所需要的条件，思路混乱，找不到解决问题的突破口。学生的解题意图，是把12.42 分米看成圆柱的底面周长，通过底面周长求出底面直径，再用两个直径的长与12.42 相乘，然而，这样求到的既不是做成的圆柱的体积，也不是圆柱的表面积。

2.数据关系理解不透。

不少学生对与圆柱展开图相关的数据理解得不够透彻，不能将展开图上的数据与圆柱各部分建立正确的联系，因而不能根据所给出的图形正确判断出“圆柱的底面周长等于涂色长方形的长”“12.42分米即是圆柱的底面直径与底面周长的和”。

【对策】

1.搭建思维坡度，经历思考过程。

我们可以适当改变题中提供的条件，降低思维难度，帮助学生厘清数量关系。

比如，可以组织学生先找出下面这张图上数据与圆柱各部分之间的关系，求出圆柱的体积。做成的圆柱的底面直径是6÷2=3（分米），则底面周长是3π 分米，而图中涂色长方形的长就等于圆柱的底面周长，由此，涂色长方形的长=圆柱底面周长=圆周率×圆柱底面直径。

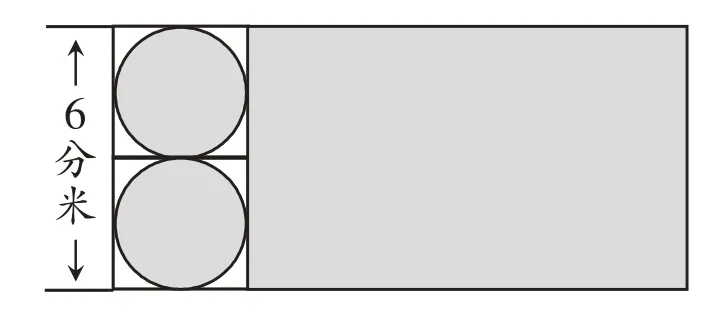
2.深入数学本质，排除无效信息。

我们可以引导学生进一步思考、讨论：能不能用涂色长方形的宽作为圆柱的底面周长？用涂色长方形的长作为圆柱的高？使学生明白，由于涂色长方形的宽正好是圆柱底面直径的2 倍，因此，不能作为圆柱的底面周长，所以圆柱的高一定是6分米，而圆柱的底面直径是3 分米。知道了圆柱的底面直径和高，它的体积也就可以求出了。

3.沟通前后联系，提升数学思维。

厘清数据之间的关系后，我们可以结合错例，重点引导学生讨论三个问题：一是涂色长方形哪条边作为圆柱的底面周长？二是涂色长方形哪条边作为圆柱的高？三是12.42 分米由哪几部分组成，又是怎么得到的？

经过讨论交流，学生能够明白：要把涂色长方形的长作为圆柱的底面周长，宽作为圆柱的高，而12.42 分米就是圆柱底面周长与一条直径的和。由πd+d=（π+1）d 可知，可以通过12.42÷（π+1）求出圆柱的底面直径是3 分米，圆柱的高是3×2=6（分米），在此基础上，再求圆柱的体积便不难了。

【练习】

张师傅剪出如图所示的一张长方形铁皮中的涂色部分，正好可以做成一个圆柱。

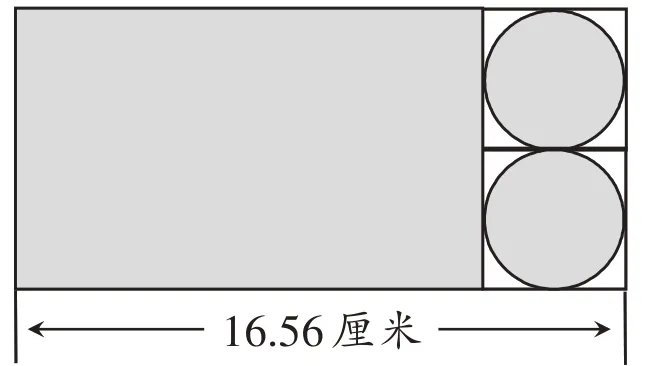
（1）这张长方形铁皮的面积是多少平方厘米？

（2）做成的圆柱的体积是多少立方厘米？

【错例】

把一个长10 厘米、宽8 厘米、高6 厘米的长方体木头，切成一个圆柱。切成的圆柱体积最大是多少立方厘米？

错解一：π×（10÷2）2×8=200π（立方厘米）

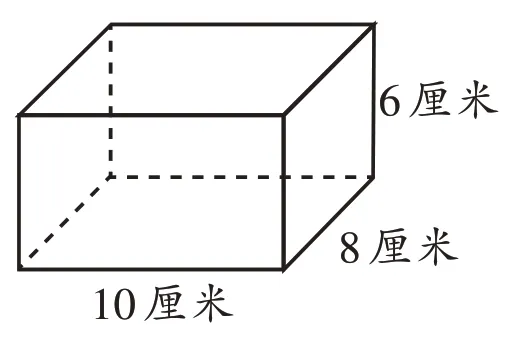
答：切成的圆柱体积最大是200π 立方厘米。

错解二：π×（6÷2）2×10=90π（立方厘米）

答：切成的圆柱体积最大是90π 立方厘米。

正确答案：

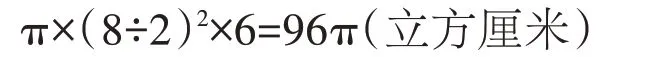
答：切成的圆柱体积最大是96π 立方厘米。

【诊断】

1.望文生义，缺少与生活实际相结合的数学思考。

看到“切成的圆柱体积最大”，学生马上想到要用最大的两个数，分别作为圆柱的底面直径和高，而不是从实际做成的圆柱体与长方体木头之间的关系，去分析、思考要把哪个面作为圆柱的底面，把哪条边作为圆柱的高。

2.思维简单化，不善于从整体上把握关键问题。

多数学生没有从整体上思考这道题可能会有几种结果，然后把各种结果进行比较，从中找出最大的体积。也有的学生想当然地认为，长方体的底面是长10 厘米、宽8 厘米的长方形，所以圆柱的底面也只能从这个长方形中截取，尽管答案可能是正确的，但思考的过程却是有瑕疵的。

【对策】

1.整体把握，多角度思考问题。

引导学生从整体入手，如果先不看“最大是多少”，一共有几种情况。可以先解决当圆柱的高是多少厘米时，它的底面直径是多少厘米。经过分析，一共有三种情况，分别是当圆柱的高是6厘米时，底面直径是8 厘米；当圆柱的高是8 厘米时，底面直径是6 厘米；当圆柱的高是10 厘米时，底面直径是6 厘米。

2.分别计算，比较中确定结果。

有序算出三种情况的结果，并通过比较确定最大值。当高是6 厘米，底面直径是8 厘米时，体积为π×（8÷2）2×6=96π（立方厘米）；当高是8 厘米，底面直径是6 厘米时，体积为π×（6÷2）2×8=72π（立方厘米）；当高是10 厘米，底面直径是6 厘米时，体积为π×（6÷2）2×10=90π（立方厘米）。比较后可知，切成的圆柱体积最大为96π立方厘米。

【练习】

1.用一块长15.7 米、宽12.56 米的铁皮，围成一个最大的圆柱体的粮仓（接头不计），这个粮仓的体积是多少立方米？

2.把一个长7 分米、宽6 分米、高9 分米的长方体木块，削成一个体积最大的圆柱。这个圆柱的体积是多少立方分米？

3.把一个长4 分米、宽2 分米、高3 分米的长方体木块，削成一个体积最大的圆锥。这个圆锥的体积是多少立方分米？

【错例】

如图，一个鱼缸中放有一块高是28 厘米、体积是4.8 立方分米的假山石，如果打开自来水管向鱼缸注水，那么至少放多少水才能将假山石完全淹没？

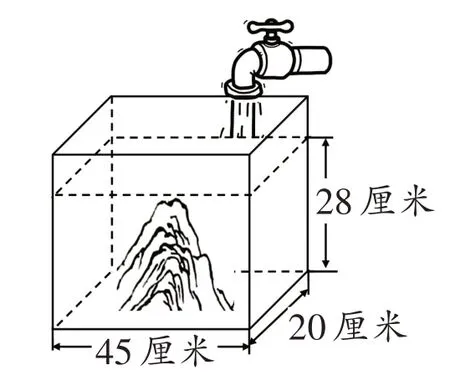
错解一：

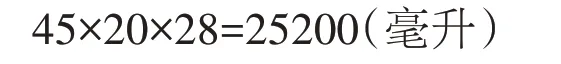
答：至少放25200 毫升的水才能将假山石完全淹没。

错解二：

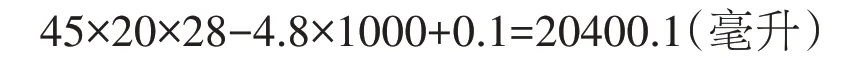
答：至少放20400.1 毫升的水才能将假山石完全淹没。

正确答案：

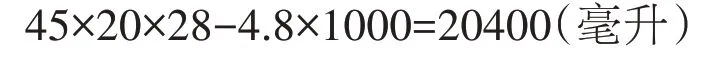
答：至少放20400 毫升的水才能将假山石完全淹没。

【诊断】

1.审题能力欠缺，遗漏关键信息。

学生审题时，没有把关键信息充分提取出来，体积为4.8 立方分米的假山石本身就在鱼缸之中，有的学生忘记了鱼缸中的假山石也占体积，以为求出长方体鱼缸中无假山石时28 厘米高的水的容积就可以了。

2.缺乏生活经验，误解关键词语。

有的学生读题时，看到“淹没”一词，误以为既然水是淹没了假山石的，那么水的高度一定是高于假山石的高度，因此，当计算出放入鱼缸里的水的容积后，还要随意地加进去一些水，如错解二中，学生多加了0.1 毫升的水。

【对策】

1.形成审题习惯，培养审题能力。

教师要引导学生充分重视良好审题习惯的培养。比如：拿到题后，首先要细读文字，理解题意；接着要抓住关键字词，圈圈画画、细心推敲，寻找数量关系，形成解题思路；解题后还要检验，或是根据生活实际进行估计，或是把算出的结果作为条件代入，或是运用其他方法计算验证。

2.加强对比辨析，实现自我纠错。

可以把错误的解法和正确的解法放在一起，让学生在比较中找出错误原因，明晰解题注意点，纠正错误思路。可以设计同类的、相关的题组，引导学生比较条件、问题和解题过程，通过互动交流、相互提醒，明晰问题本质，比如审题不可马马虎虎、同一题中的单位名称要一致等。

【练习】

1.一个长方体水箱，长7 分米、宽6 分米，水深5 分米。把两个同样大小的铁球完全浸没在水中，水面上升到8 分米处。每个铁球的体积是多少立方分米？

2.小明在一个长10 厘米、宽10 厘米、高15 厘米的长方体容器中加入一些水后，测量一块石头的体积。当把石头浸没在容器中时，容器上口有水溢出。当把石头从容器中取出来后，水面下降到10 厘米高的刻度处。这块石头的体积是多少立方厘米？

3.一个盛水的长方体容器，长5 厘米、宽4 厘米、高10 厘米。里面水深2 厘米，现将一个棱长3厘米的正方体铁块垂直放入容器底部。长方体容器中现在水深多少厘米？

统计与概率

【错例】

一个骰子六个面上的点数分别是1 到6。同时掷两枚骰子，如果点数和是5、6、7、8、9 中的一种，判定老师赢，否则学生赢。（学生）赢的可能性比较大，因为（同时掷两枚骰子，点数和从2 到12，共有11 种可能，老师有5 种赢的可能，而学生有6 种赢的可能）。

正确答案：

（老师）赢的可能性比较大，因为（同时掷两枚骰子，点数和共有36 种可能，老师有24 种赢的可能，而学生只有12 种赢的可能）。

【诊断】

1.题意理解浅表化。

可能性虽然是生活中常见的现象，但将其从生活中抽象出来，用数学的眼光来看，学生又会感觉比较陌生。从而导致学生对于题意的理解浮于表面。比如，学生会错误地以为，同时掷两枚骰子，点数和共有11 种可能，老师选了5 种，则学生选6种，6种大于5种，所以学生赢的可能性比老师大。

2.策略选择不恰当。

解决问题时，学生忽略了“同样的结果，可以由两枚不同骰子上的数相加得到，比如1+2 跟2+1，是两种不同的情况”，因此，不能简单地从两枚骰子上的点数和有11 种，就确定谁赢的可能性大，而要从排列组合的角度，去思考每种结果可能性的大小，再来判断谁赢的可能性大。

【对策】

1.组织探究活动，经历实践操作过程。

事件发生的可能性的大小，需要通过实践来验证。教学时，要创设学生参与的情境，选择学生感兴趣的活动题材作为探究素材，引导学生充分经历“提出猜想——收集、整理数据——分析数据”的过程，既能丰富学生感受事物发生可能性大小的直观体验，又能感悟不确定现象的特点。

2.重视解题策略，发展数据分析观念。

引导学生在仔细观察、大胆猜测、充分实验、互动交流的过程中，体验可能性的大小，培养和发展统计与数据分析观念。必要时，可以借助一一列举的策略，直观形象地表示出所有出现的可能，借此弥补学生经验上的不足，澄清认识上的误区。比如，“两枚骰子的点数和有多少种”“老师、学生赢的可能性各有多少种”等问题，可以通过一一列举的方法找到正确的答案，具体如下表。

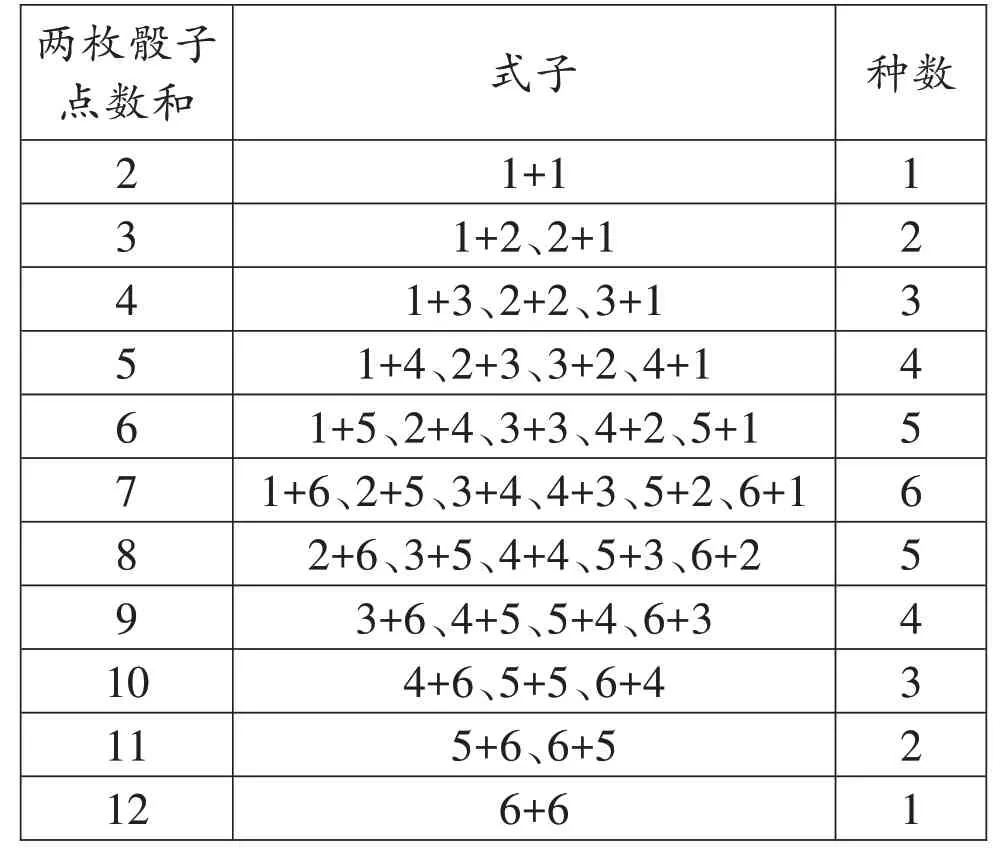
两枚骰子__点_______________________________________数和种数____2______________________3____________________4 5 6______________7________________8____9___________________10_____________________11________________________12式子1+1 1+2、2+1____________1+3、2+2、3+1__________1+4、2+3、3+2、4+1 1+5、2+4、3+3、4+2、5+1 1+6、2+5、3+4、4+3、5+2、6+1____2+6、3+5、4+4、5+3、6+2______3+6、4+5、5+4、6+3________4+6、5+5、6+4__________5+6、6+5____________6+6_______________1___2___3___4___5___6___5___4___3___2___1___

【练习】

1. 八张卡片上分别写有1、2、3、4、5、6、7、8，每次任意摸出一张，摸到比4 大的姐姐赢，摸到比4小的妹妹赢。（ ）赢的可能性比较大。

2.用7、8、9这三张数字卡片，可以组成（ ）个两位数，其中组成（ ）（填“奇”或“偶”）数的可能性比较小。

3.把写有数字1 到9 的九张卡片，倒扣在桌面上，打乱顺序后，任意摸出一张，摸到（ ）的可能性最大。

A.质数 B.合数

C.奇数 D.偶数

【错例】

六年级一班第一小组学生身高情况如下表。这个小组学生的平均身高是多少厘米？

身高/厘米___人数/人143 1_____145 3____149 5_____155_1___

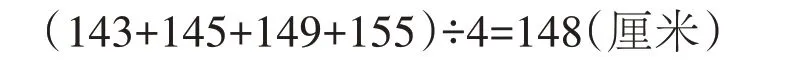
答：这个小组学生的平均身高是148 厘米。

正确答案：

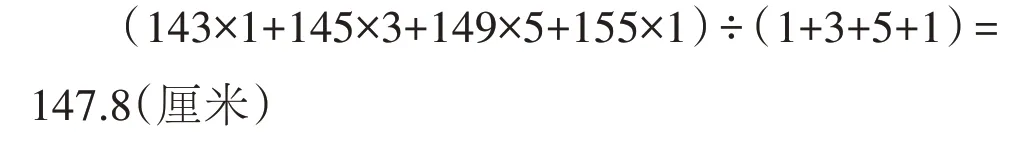
答：这个小组学生的平均身高是147.8 厘米。

【诊断】

1.平均数意义的理解不深刻。

平均数这个统计量在统计学上的意义，是能够刻画、代表一组数据的整体水平。通过学习，至少需要学生从三个方面理解其意义：一是应用“移多补少”求平均数。二是应用“先合再分”求平均数，即根据“总数量÷总份数=平均数”来求。三是明确一组数据的平均数的范围是在最小数和最大数之间。从错解可以看出，学生虽然记住了求平均数的数量关系式的形，但对平均数意义的本质的理解还存在偏差。

2.数据统计和分析的训练不够。

日常解决平均数的问题，通常都是用文字直接叙述的，像这种将统计和平均数相结合的题，学生接触相对较少。如果教师没有带领学生经历过“先统计原始数据，再将原始数据分类整理、绘制统计图表，最后根据统计图表上的数据信息，进行合理分析、描述、解决问题”的完整过程，学生想读懂这道题，是有一定难度的。

【对策】

1.经历过程，有效理解平均数的意义。

要从统计学的角度学习平均数,让学生在经历完整的统计活动的过程中，不断体会、感悟、理解平均数的意义；要在绘制统计图表的过程中，培养学生读图的能力；要在用数据描述、分析统计图表的过程中，深化学生对“平均数是一种统计量”的理解。

2.自主探索，培养学生的数据分析观念。

创设合理情境（如从两组人数不等的学生中，选拔投篮水平较高的一组，参加更高等级的比赛），促进学生自主探究求平均数的方法——移多补少或先合再分。引导学生在对两种方法的比较中，感悟它们的共同点。同时，适时渗透平均数的范围在最小数和最大数之间，以及平均数能反映出一组数的整体水平，但不能代表每个个体的情况，平均数受极端数据的影响较大，帮助学生更加深刻、全面地理解平均数。

【练习】

1.一个书架上，第一层放了36 本书，第二层放了42 本书，第三层和第四层共放了54 本书。平均每层放了多少本书？

2.在上学期期末测试中，六年级二班的平均分是95 分。老师给第一小组学生记分如下：

姓名__分数____学生1__+3_____学生2__+5______学生3__0______学生4__-3______学生5__-1_____学生6__+5______学生7__-1______学生8 0___

那么第一小组的平均分是多少分？

3.甲、乙、丙、丁四个人的年龄中，最大的45岁，最小的24 岁。那么他们四人的平均年龄有可能是（ ）岁。

A.46 B.40

C.24 D.20

【错例】

1.下面是六年级一班学生一至六年级时的近视率记录表。要反映近视率的变化情况，可选用（C）统计图。

?

A.条形 B.折线 C.扇形

正确答案：

B

【诊断】

1.思维定势干扰，审题马虎。

扇形统计图的特征是能表示各部分数量与总数之间的关系，学生学习扇形统计图时，见到的数据很多都是百分数，误以为只要是有百分数数据的统计图，就一定是扇形统计图。受这种负迁移的影响，看到“百分比”三字，学生就毫不犹豫地选择C，而忽略了题目的要求是“反映近视率的变化情况”。

2.提取信息能力不足，盲目选择。

学生对于条形统计图、折线统计图和扇形统计图各自的特征理解不深，不善于抓住关键信息处理问题。比如，需要清楚地反映数量的多少可以选用条形统计图或折线统计图；需要直观地看出数据增减变化的情况宜选用折线统计图；需要清楚地看出各部分数量与总数之间的关系应选用扇形统计图。三种统计图虽有不同，但也有联系，有时可以同时选择两种统计图来解决问题，导致有的学生无所适从。

【对策】

1.注重学习，夯实基础。

教材把扇形统计图安排在六年级学习，而条形统计图、折线统计图在四、五年级就学习了，中间跨度比较大，容易发生知识遗忘现象。因此，在学习扇形统计图前，要加强对条形统计图、折线统计图知识的复习，为学习新知打下扎实的基础。

2.抓住特征，比较提升。

为了能够正确选用统计图，学生掌握扇形统计图的特征和作用后，应适当加强对三种统计图的比较，帮助学生厘清三者之间的联系和区别，明晰各自的概念和适用范围。解决问题时，要着重培养学生认真审题和信息提取、解读的能力，比如查找隐含信息的能力、删除多余信息的能力、圈出关键信息的能力等，有利于学生抓住问题本质，合理选择解决问题的方法。

【练习】

1.某社区要反映本区域内人口年龄结构，他们选用（ ）统计图，能更清楚地看出各个年龄段的人数占总人数的百分之几。

A.条形 B.折线 C.扇形

2.表示一位病人一天内体温的变化情况，绘制（ ）统计图比较合适。

A.条形 B.折线

C.扇形 D.无法确定

3.电器商场的王经理计划制作一个统计图，需要能够清楚地表示出4 个商场8 月份甲、乙两种空调的销量情况，制成（ ）统计图比较好。

A.扇形 B.复式扇形

C.复式条形 D.复式折线

【错例】

一天，明明去上学。他刚走不久，妈妈发现他忘记带数学书了，于是就去追明明。

（1）妈妈出发时，明明已经走了（300）米，他的速度是（300）米/分。

（2）照这样的速度，妈妈出发后（4）分钟可以追上明明。

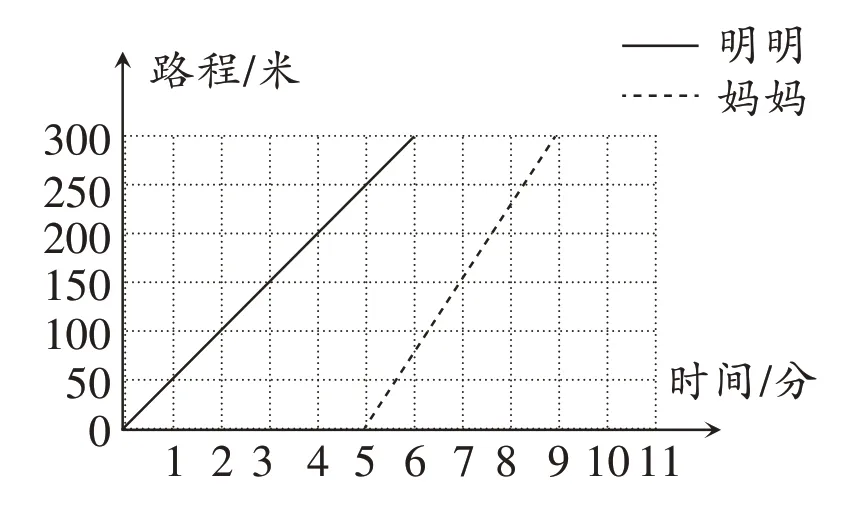
正确答案：

（1）妈妈出发时，明明已经走了（250）米，他的速度是（50）米/分。

（2）照这样的速度，妈妈出发后（10）分钟可以追上明明。

【诊断】

1.获取图像化数学信息的能力不足。

图中反映的是路程与时间的关系，学生应直接从图中读出：明明出发（ ）分钟时走了（ ）米；妈妈出发时，明明已经走了（ ）米，妈妈出发（ ）分钟时走了（ ）米。还要通过直接读出的信息，间接读出：明明的速度是（ ）米/分，妈妈的速度是（ ）米/分，妈妈出发后（ ）分钟可以追上明明。如果直接用文字进行描述，或许学生能够理解，但用图像来表征这些数学信息，学生的理解力就显得有欠缺。

2.数量关系分析不当。

从图中所画的两条线段的趋势来看，都是呈正比例关系，即“路程÷时间=速度（一定）”，可以抓住图中某些关键的点进行数量关系的分析。但因读图能力较差，学生对数量关系的理解与分析都存在问题，导致错解。

3.数学知识应用能力不足。

很多学生不能将数学问题与生活中的数学建立联系，当遇到从生活中提炼出来的数学问题时，往往不能运用所学的数学知识去解决实际问题。

【对策】

1.结合生活实际，注重感悟数量关系。

教师要善于引导学生将数学与生活建立联系，无论从文字上，还是从图表中，都能读懂那些富有生活气息的数学信息，让学生经历从生活中提炼数学信息的过程，充分理解、感悟相互间的数量关系。

2.加强识图训练，培养数据分析能力。

教师要尽可能地为数据赋予生活实际背景，多从图表中数据的含义、读图绘图的方法入手，培养学生既能很快识别直接信息，又能从中推导出间接信息的能力。

3.探寻解题策略，多法并举优化思路。

当引入图表反映数量关系后，除了将图上数据与原有的文字建立联系外，有时还可以运用直观的方法，解决图表上的问题。比如这道例题，可以让学生拿出笔和尺，按照两条线段的发展趋势画一画，它们的交点处即是妈妈追上明明的地方，只要图表画得精准，我们就能一眼看出，妈妈追上明明时，是在离家多少米处，是在明明和妈妈各自出发了多长时间的时刻。

【练习】

客车从甲地开往乙地，货车从乙地开往甲地，行驶的情况如图。

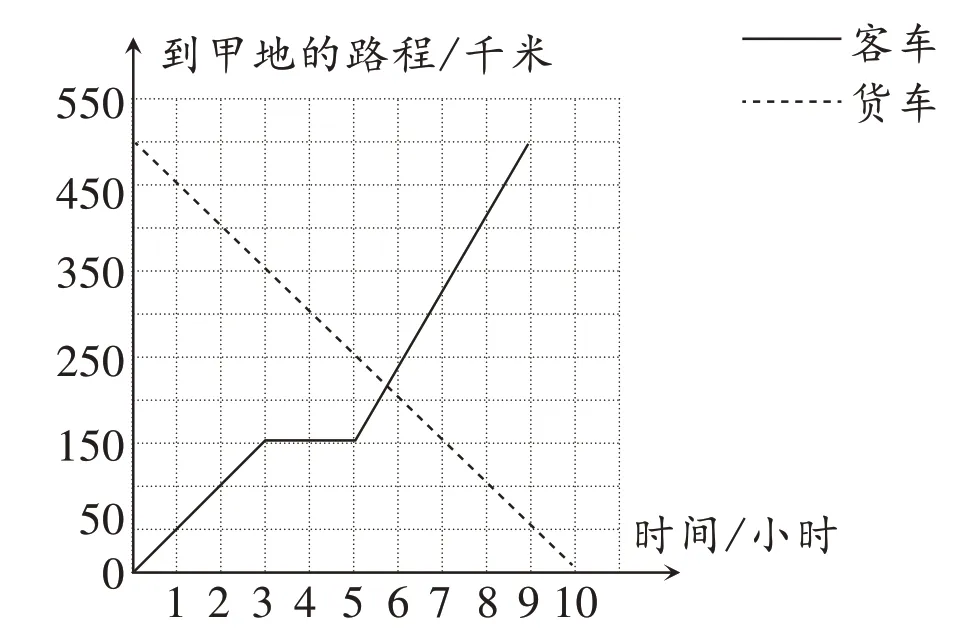
（1）货车所行的路程与时间成（ ）比例关系。

（2）客车在距乙地（ ）千米的地方停留了（ ）小时。

（3）客车与货车相遇时，客车大约行驶了（ ）小时，相遇地点距甲地大约（ ）千米。

【错例】

某市音乐考试进行改革，考试结果以等级形式呈现，分甲、乙、丙、丁四个等级。幸福小学六年级为了迎接毕业考试，进行了一次模拟考试，随机抽取部分学生的音乐成绩进行调查统计，绘制成如下两幅不完整的统计图。如果该校六年级共有250 名学生，估计一下，这次模拟考试有多少名学生的音乐成绩等级为丁？

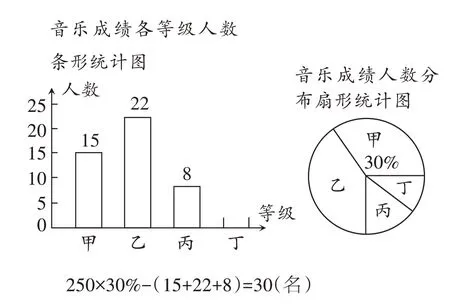
答：这次模拟考试有30 名学生的音乐成绩等级为丁。

正确答案：

答：这次模拟考试有25 名学生的音乐成绩等级为丁。

【诊断】

1.未能有效关联统计图间对应信息。

条形统计图与扇形统计图是对同一事件的两种不同的表达，学生缺少对扇形统计图的充分认知，不能把扇形统计图中的信息与条形统计图中的信息进行有效整合。

比如，考得甲等级的学生，从条形统计图中可以知道有15 人，从扇形统计图中可以知道是占抽取统计总人数的30%，进而可以求出抽取统计的总人数是15÷30%=50（人）。

2.没有有效建构数量关系知识体系。

由于数量关系比较复杂，涉及部分量与总数之间的关系、具体数量与对应分率的关系、抽取人数与总人数之间的关系等，对于学生而言，具有很大的挑战性。

比如，同一个30%，从抽取样本角度看，是指抽到的得甲的人数占抽取总人数的30%；从总体情况角度看，也可以表示六年级所有参加考试的人数中，得甲的人数占30%。如果没有真正读懂题目中的信息，并对这些信息进行分析、有效建构关联，就只能望“题”兴叹了。

【对策】

1.促进知识内与知识间的关联。

既要形成同一个知识体系内各知识点之间的关联，也要促进不同知识体系之间的关联。比如，扇形统计图是以圆和扇形的知识作为基础的，教学中可以适当增加扇形知识内容的教学，让学生更加充分、深刻地认识扇形统计图的特征和用途。同时，联系百分数的意义，将两幅统计图中得甲的信息进行分析，理出解决问题的思路。

2.提升信息获取和加工的能力。

平时的学习中，要有意识地培养学生文本信息、图表信息的获取与加工能力。要引导学生从宏观和微观两个层面正确把握数学信息，既要从整体上观察统计图中的项目信息，看出各部分占总数的百分数，又要寻找同一图表内和不同图表间各信息的对应关系，在比较中加深理解，确保问题得到解决。

【练习】

在一次打击电信网络诈骗犯罪专项行动中，希望小学学生开展了“防止电信网络诈骗”的调查活动。同学们将调查结果整理分析后，正在绘制统计图。

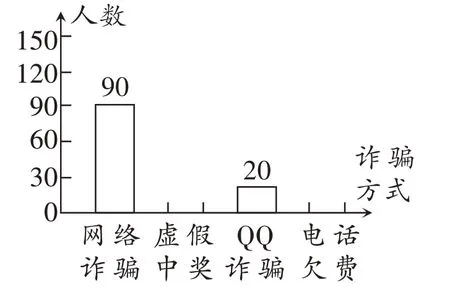
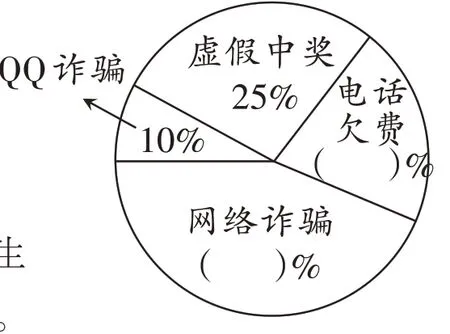
（1）希望小学学生一共调查了（ ）人。

（2）完成上面的统计图，并写出有关的计算过程。