感应电机无差拍模型预测转矩控制研究*

孙君放， 解 伟， 陈祥林， 林晓刚， 赵宇纬

(1.福州大学 电气工程与自动化学院，福建 福州 350108；2.中国科学院海西研究院 泉州装备制造研究所，福建 泉州 362000)

0 引 言

模型预测控制(MPC)是20世纪70年代后期出现于工业工程控制领域的一类计算机控制算法，在过程控制行业得到广泛应用[1]。20世纪80年代中期在电力传动领域中提出应用模型预测控制的思想[2]。但因MPC计算量较大的原因，受微处理器硬件的限制，在实时性要求较高的电力传动领域应用较少[3]。

随着数字信号处理器持续发展，MPC逐渐成为功率转换和驱动器控制中新兴的替代方法，相比于高性能交流变频器的标准解决方案的2种传统策略：磁场定向控制(FOC)和直接转矩控制(DTC)。该方法具有动态响应迅速、控制灵活等优势，在交流电机控制领域得到了广泛应用[4-6]。

MPC策略根据优化方式和作用场合，可大致分为连续控制集模型预测控制(CCS-MPC)和有限控制集模型预测控制(FCS-MPC)[7-10]。与CCS-MPC相比，由于FCS-MPC易于非线性和约束控制，具有很好的鲁棒性及实际应用[11]。应用于电力传动领域的FCS-MPC根据其控制目标的不同又大致可分为预测电流控制(PCC)和预测转矩控制(PTC)。PCC和PTC均是以控制变量的误差最小化为目标设计价值函数选出最佳电压矢量并输出下一时刻相应的开关状态。PCC仅考虑电流参考值与实测值之间的误差，其计算时间快，但由于其不是直接以电磁转矩为控制目标，难以确保电磁转矩的控制效果[12-13]；PTC利用权重系数把转矩和磁链参考值与预测值之间差值构成价值函数进行预测，其静动态性能良好，且具有较小的转矩脉动[14]。但预测过程中每次需要对所有可行电压矢量(VV)的进行预测，从而增加了计算成本，降低了效率。随着无差拍(DB)控制出现，在选择最佳电压矢量的过程中，用所需电压矢量组成的预测DB电压扇区进行枚举选择[15]，KENNL[16]首先将DB控制应用到电驱动系统中，并提出完整建模和实验验证；文献[17]中将DB控制运用在永磁同步电机(PMSM)驱动系统中，减少了系统的计算成本，并在试验结果中验证了所提控制策略的有效性。而对于DB控制在感应电机(IM)驱动系统中应用的研究则较少。

本文通过建立IM的动态数学模型，在传统的FCS-MPC基础上，结合DB控制，将预测DB电压扇区内的电压矢量作为枚举选择，计算得到最佳电压矢量并输出相应开关状态，减少在线滚动优化次数，从而缩短预测过程，降低算法计算成本。通过仿真，在减轻系统计算负担情况下，DB-PTC可以得到与传统PTC几乎相同的稳态跟踪性能。

1 数学模型

1.1 IM动态数学模型

在任何参考坐标系下，电机旋转角频率ωs表示，转子角速度ωr表示，IM动态数学模型可表示为[14]

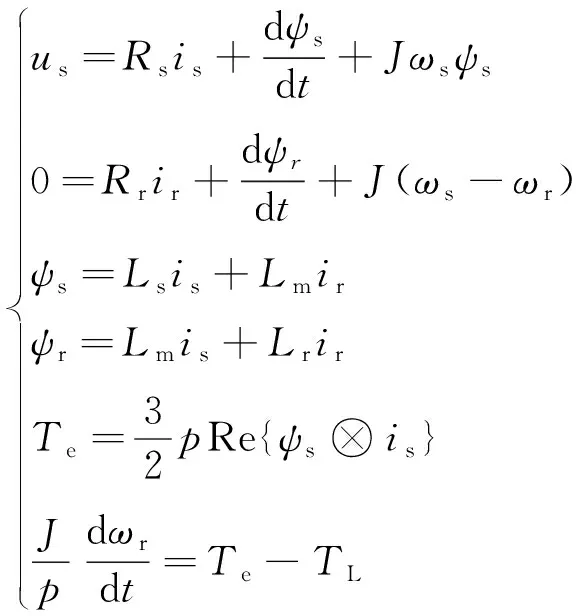
(1)

式中:Ls、Lr和Lm分别为定子、转子和励磁电感；Rs和Rr分别为定子电阻和转子电阻；us和is分别为定子电压和电流矢量；ir为转子电流矢量；ψs和ψr为定子和转子磁链矢量；Te和TL分别为电磁转矩和负载转矩；p为极对数；J为电机转动惯量。

1.2 电压逆变器模型

IM预测转矩控制系统中利用两电平电压源逆变器(2L-VSI)进行供电，每相电路对应2个开关器件(1为上桥臂的开关器件开通，下桥臂关断，0为下桥臂的开关器件开通，上桥臂关断)，在三相电路中开关状态组成6个有效电压矢量和2个零矢量，具体如表1所示。

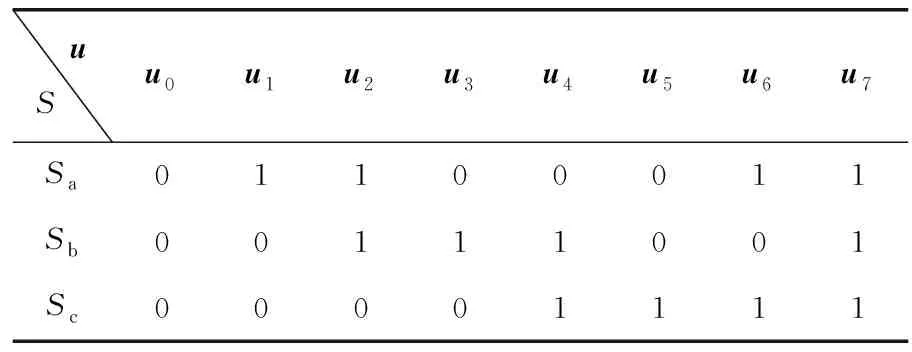
表1 2L-VSL开关表

基于静止坐标系下的电压为

uαβ=UDCTCSabc

(2)

式中：UDC为直流母线电压;Sabc为开关状态;TC为Clarke坐标变换矩阵，

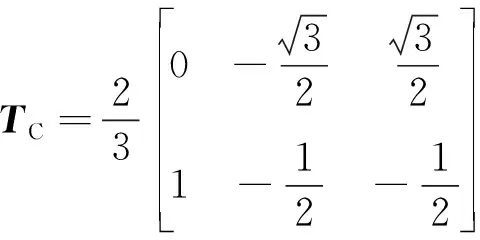
(3)

2 IM传统PTC

IM传统PTC系统结构框图如图1所示。

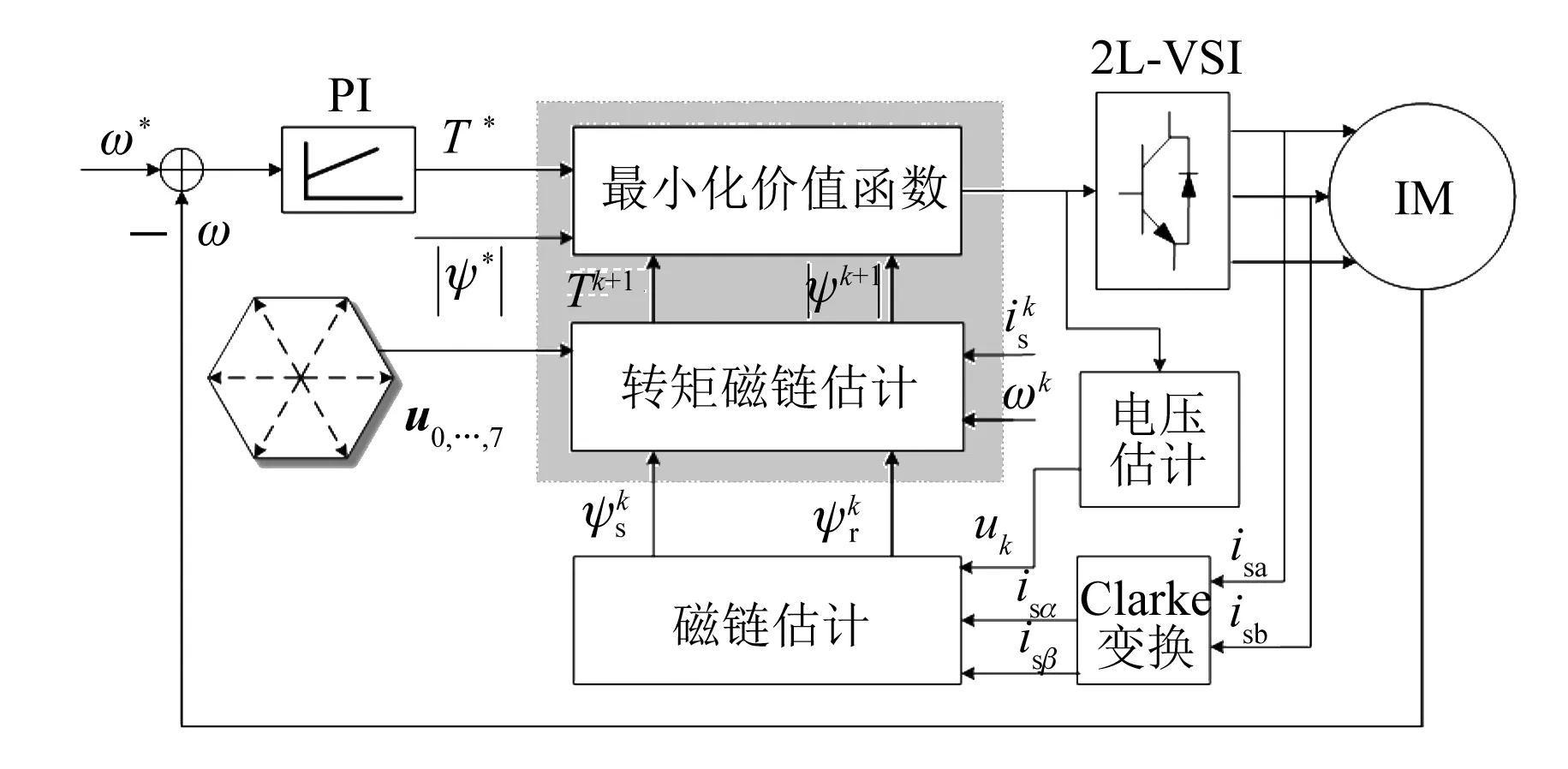
图1 传统PTC系统框图[11]

传统PTC利用目标函数的线性组合构建的单个价值函数，对所有可行电压矢量进行枚举选择，根据枚举结果确定下一个采样时刻的最优矢量[18]。

2.1 磁链估计

传统PTC中，通过估计电压和电流，利用式(4)和式(5)分别对定子磁链和转子磁链进行估计[19]：

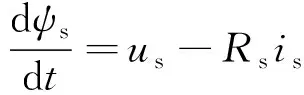
(4)

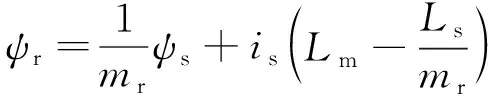
(5)

为预测下一采样k+1时刻磁链，要利用欧拉公式对式(4)和式(5)进行离散化，完成对当前k时刻磁链的估算[20]：

ψs(k)=ψs(k-1)+Tsus(k)-

RsTsis(k)

(6)

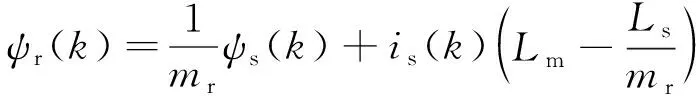
(7)

2.2 预测转矩

通过测量定子电压电流，可根据式(8)预测下个采样周期的定子磁链，根据式(9)和式(10)预测下个采样周期的转矩[21-22]：

ψs(k+1)=ψs(k)+Tsus(k)-RsTsis(k)

(8)

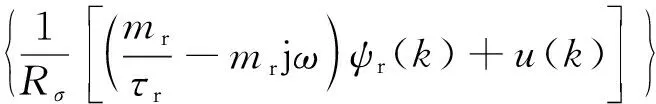
(9)

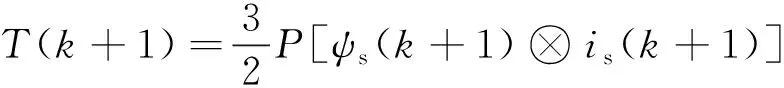
(10)

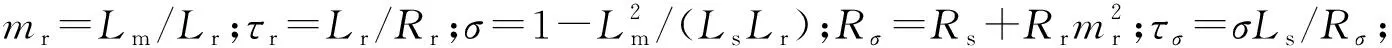
2.3 价值函数

通过预设的价值函数评估单个采样周期内所有可行的电压矢量，利用误差最小化原理确定最优电压矢量。本文中，选取转矩和磁链作为价值函数的参考目标：

g=|Tref-T(k+1)|-λ|ψref-ψs(k+1)|

(11)

式中:Tref和ψref分别为转矩和定子磁链的参考值，利用权重系数λ，保证磁链和转矩具有同样优先级。

由于传统PTC单步滚动优化预测过程需经过8个VV优化预测，计算成本高，实施难度大。

3 DB优化策略

本文提及的DB-PTC是基于DB理论，估算下一时刻所需的DB电压矢量(DB-VV)及判断其空间位置，并对基于静止两相坐标系下进行划分DB扇区(DB-Sector)，再根据空间位置确定扇区；利用误差最小化原理来评估扇区内电压矢量并输出相对应的开关状态[17]。2L-VSI的DB扇区矢量图如图2所示。

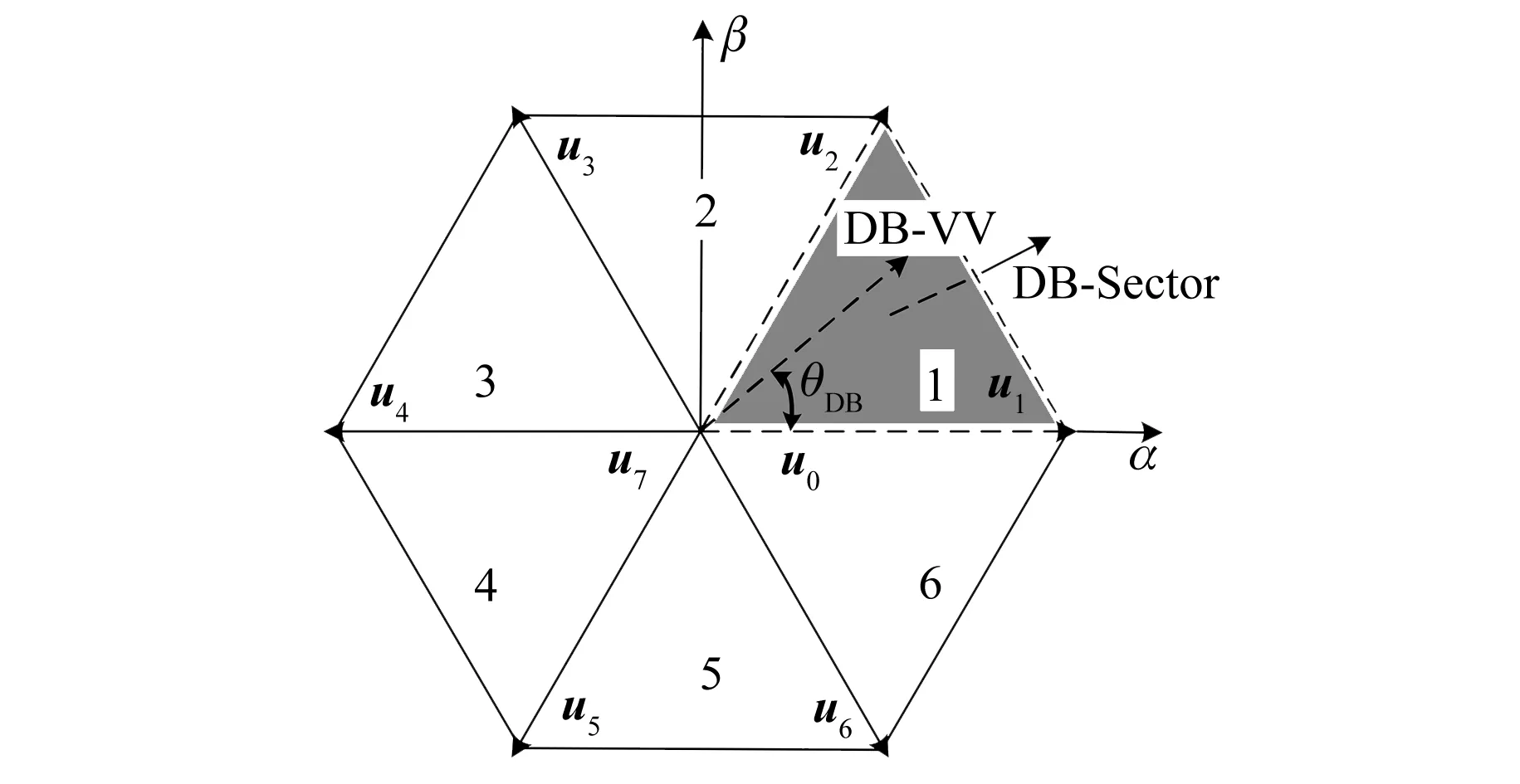
图2 2L-VSI的DB扇区矢量图[17]

3.1 DB-VV的计算

DB-PTC基于逆模型推导，根据下一采样时刻所需转矩和定子磁链的参考值来计算所需的DB-VV，通过输出DB-VV相应的开关状态，得到下个采样周期所需的电压，输出所需转矩和定子磁链[17]:

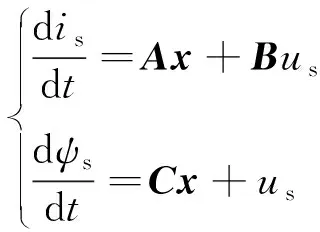
(12)

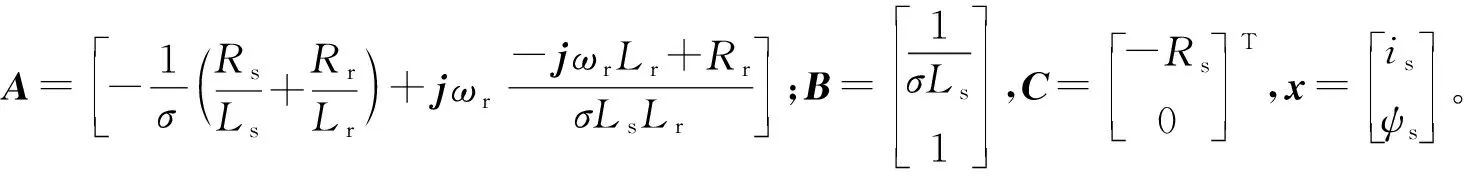
根据式(12)对定子电流和定子磁链进行预测计算时，将状态变量在静止两相坐标系下进行正交分解得到定子磁链预测值；依据式(7)可得出转子磁链预测值；再根据转矩和磁链来算出参考电压矢量[19]，计算式如下；

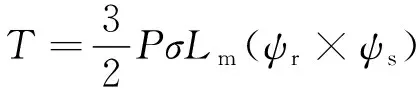
(13)

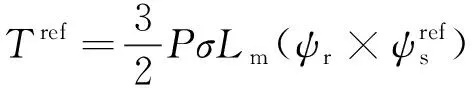
(14)

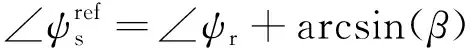
(15)

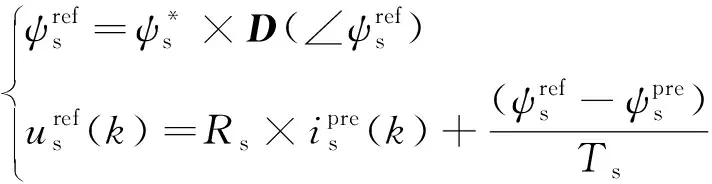
(16)

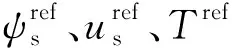
参考电压,通过式(16)解耦出静止两相坐标系下电压值uα和uβ，再确定所在扇区：

(17)

由表2可以看出，所提DB-PTC有限控制集中的元素从8个减少至3个，极大程度降低了计算负担。仅需根据邻近矢量原理进行矢量分配，将每个扇区相邻的2个有效VV和一个零VV作为扇区内的DB-VV。

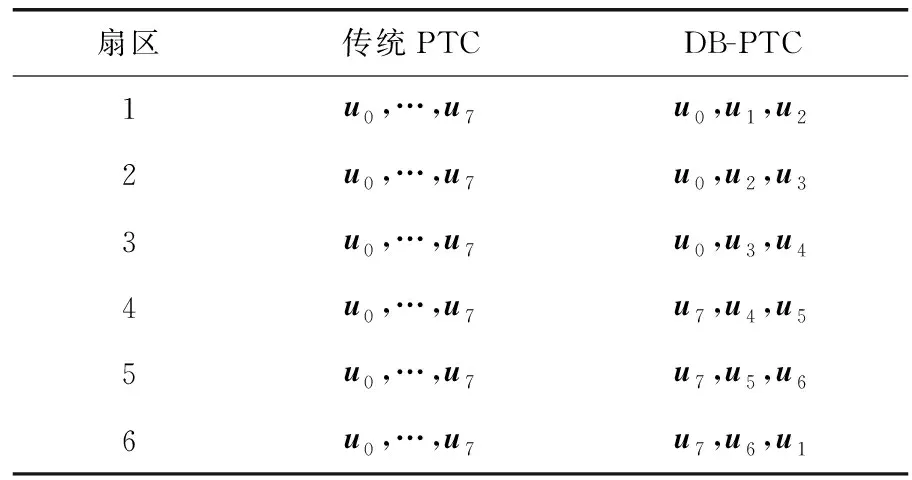
表2 DB-PTC与传统PTC矢量分配

3.2 所提算法的实现

DB-PTC通过优化预测过程，经过DB-VV的计算和DB-Sector的定义与划分之后，将预测VV优化到3个VV，再通过价值函数进行最小化评估，输出最优开关状态。

DB-PTC系统框图如图3所示，将预测过程从每步预测8个VV降低到3个VV，其整体控制算法流程图如图4所示。分为以下步骤。

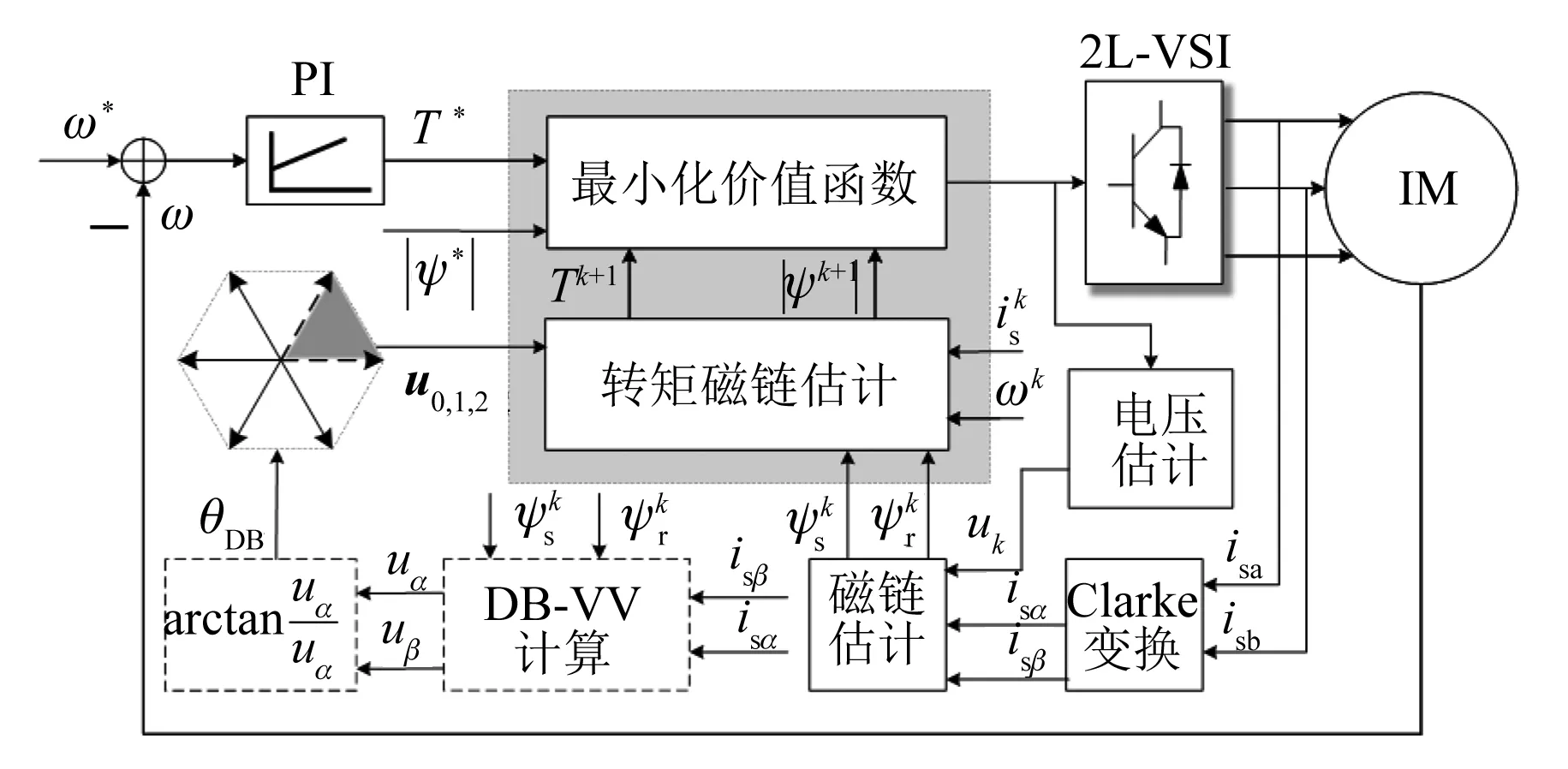
图3 DB-PTC系统框图

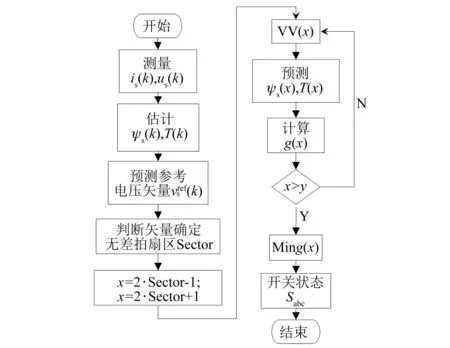
图4 DB-PTC算法流程图[17]

步骤1：测量当前采样周期的定子电流和电压；

步骤2：根据电流和电压估计当前采样周期的磁链和转矩；

步骤3：利用逆模型预测方程来估算DB-VV和进行DB-Sector划分；

步骤4：判断DB-VV空间位置，确定准确的DB-Sector，确定被测VV；

步骤5：根据磁链和转矩预测方程对被测3个VV求解出转矩和磁链，定为可行VV；

步骤6：计算所有可行VV价值函数值；

步骤7：依据误差最小化原理，选取最小价值函数值的VV；

步骤8：将选定的VV所对应的开关状态作为开关器件的门极信号输出。

4 仿真验证及分析

为验证DB-PTC控制算法的可行性，在MATLAB/Simulink平台中搭建IM仿真控制系统模型，并把传统PTC算法和DB-PTC算法进行仿真对比，以验证DB-PTC在保证稳态跟踪性能效果的前提下，可减小整体控制系统的计算成本。IM参数由表3所示。

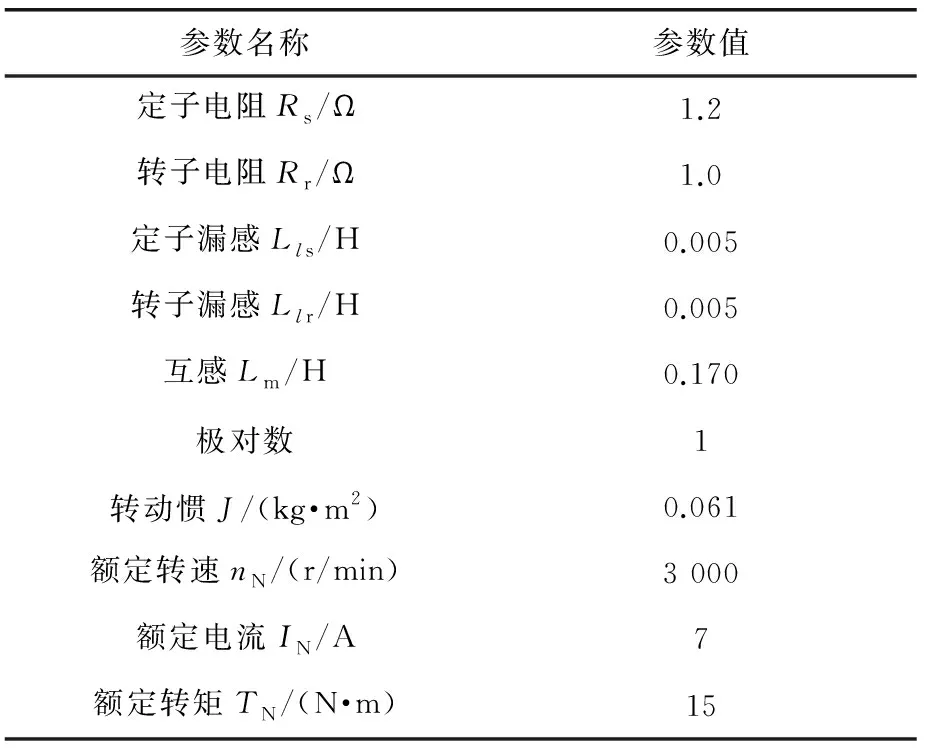
表3 IM基本参数

基于MATLAB分析器在2种算法相同仿真时间周期内，对评估矢量模块进行3次分析计算，2种算法的所需时间占比结果如图5所示。图5中可以看出DB-PTC算法在单步滚动优化过程中，仿真计算成本优化效果显著。

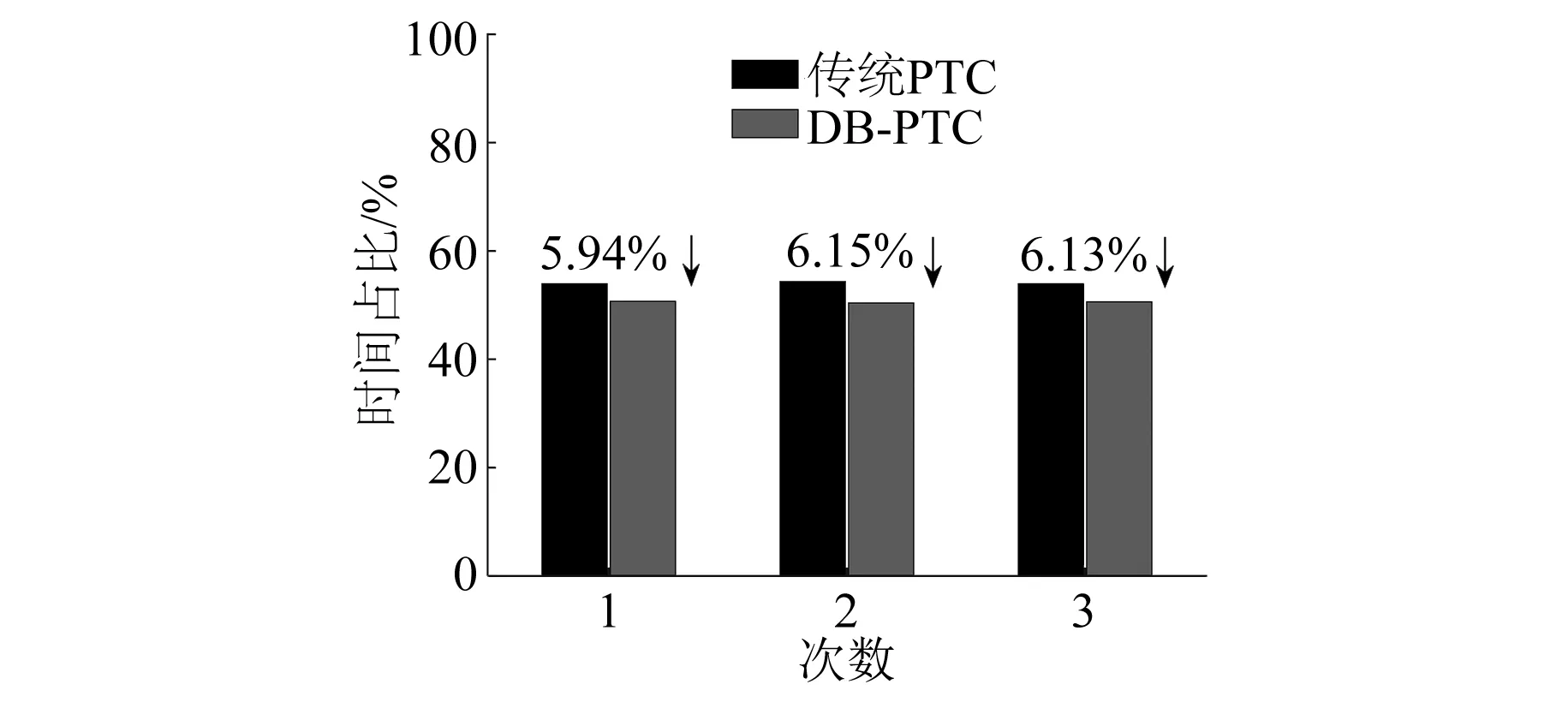
图5 传统PTC和DB-PTC计算成本

因传统PTC算法是通过选择可行VV来实现对转矩的及时响应，为验证DB-PTC算法的瞬态响应，对DB-PTC算法的可行VV的选择进行分析。

仿真过程中，2L-VSI在传统PTC算法过程中所产生的开关状态[000, …,111]，将1表示000，7表示110。负载转矩15 N·m稳态下的切换情况如图6(a)所示。

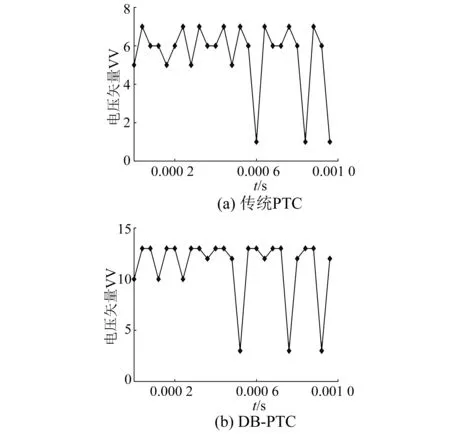
图6 传统PTC和DB-PTC稳态时开关状态

2L-VSI在传统PTC算法过程中所产生的开关状态[000, …,111]，经过扇区划分之后，为避免零矢量丢失，开关状态将表示为[100, 000, 110, 000, 010, …,100]，1表示100，13表示最后一个100进行依次排列。负载转矩15 N·m稳态下的切换情况如图6(b)所示。

在额定转速下，分别对2种控制算法进行仿真验证分析。直流母线电压为520 V；速度环PI参数为kp=10.012、ki=20，输出限幅为[-20,20]。系统仿真时间设置为0～3 s。在0、1、2 s时对电机分别施加5、15、5 N·m的负载转矩，对比2种算法稳态转矩波形。

在给定负载转矩时，图7为稳态下2种控制算法转矩波形图，可以看出 DB-PTC算法与传统PTC有几乎相同的稳态跟踪性能。

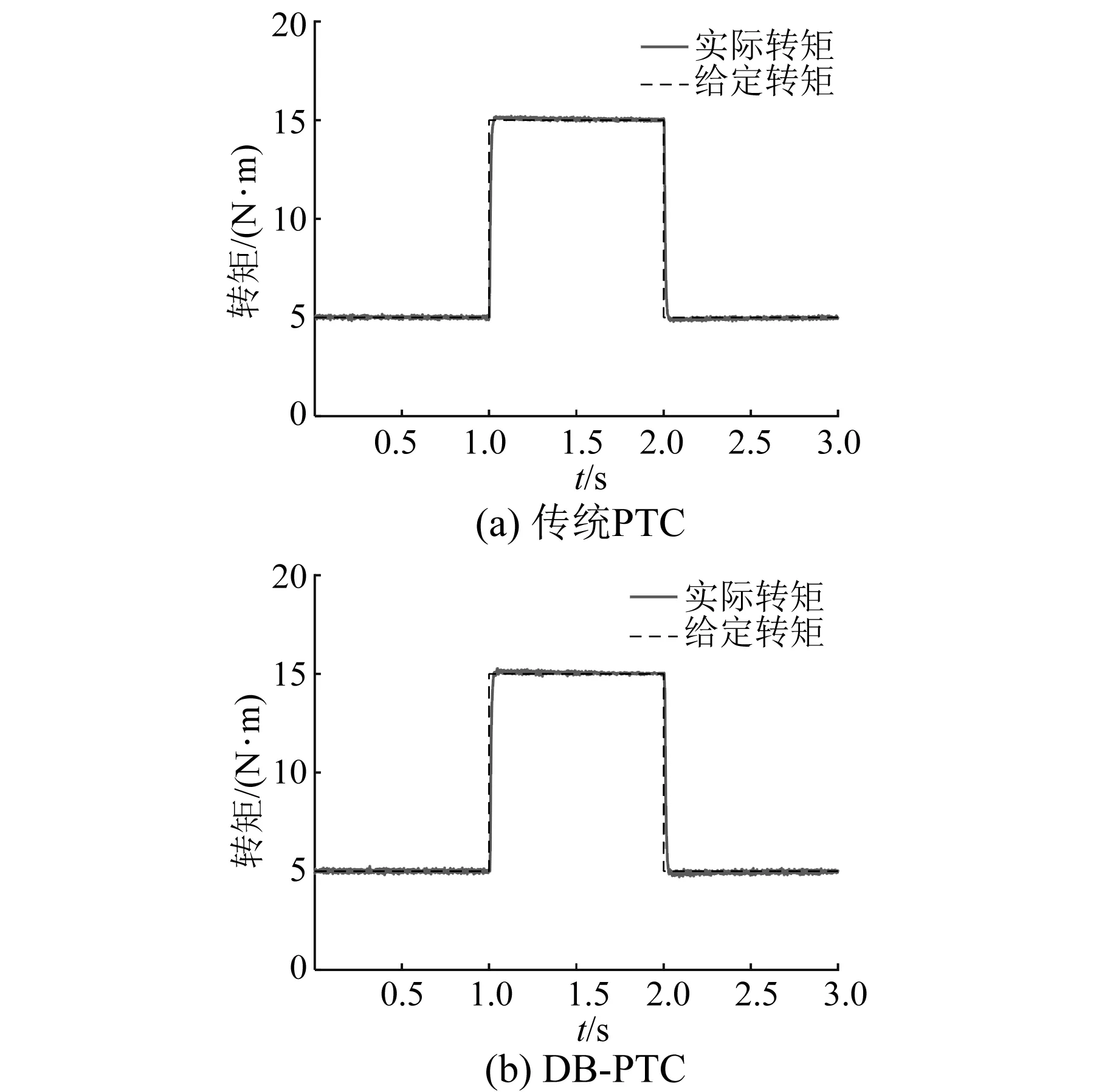
图7 电机转矩波形图

综上所述，DB-PTC算法在达到与传统PTC算法相同稳态跟踪性能情况下，在传统PTC所需时间的基础上，单步滚动优化所需时间下降了6%左右。

5 结 语

本文通过MATLAB/Simulink平台搭建的由2L-VSI供电驱动IM控制系统，基于DB控制理论的DB-PTC，通过计算DB-VV和DB-Sector划分，将单步滚动优化预测的数量由8个降低到3个，降低了算法的计算成本和提升了可操作性。并通过仿真验证，DB-PTC在优化计算成本的情况下，保持着与传统PTC几乎相同的负载转矩稳态跟踪性能。