紧凑型高压异步电机三维流体场分析及温度场仿真计算*

贾振宇, 曲兵妮, 宋建成, 赵 勇

(1.太原理工大学 矿用智能电器技术国家地方联合工程实验室，山西 太原 030024；2.太原理工大学 电气与动力工程学院,山西 太原 030024)

0 引 言

紧凑型高压异步电机内部空间结构紧凑，电机运行时产生的热量会使电机内部温度升高。当温度高于最大允许值时，就会损害电机绕组绝缘，缩短电机的使用寿命。因此，在电机设计过程中需对电机的温度场进行仿真计算。

目前已有许多学者对电机温度场进行了研究。文献[1]采用磁热顺序耦合方式，将磁场节点损耗密度结果耦合到三维温度场模型中计算了电机瞬态温度场，并以转子的瞬态温度结果为载荷，得到了转子热应力变化规律。文献[2]对高速高压电机的流体场与温度场进行了仿真,计算出电机各个通风槽内冷却气体流动情况。文献[3]对油田用感应电机进行了瞬态温度场计算，采用经验公式完成了各部件表面散热系数的计算。文献[4]根据电机冷却系统的结构特点，将整个冷却系统划分为外风扇和冷却器2个区域，用边界条件将二者联系起来对内流体场和传热情况进行了分析。文献[5]对中型高压异步电机及其冷却器进行了流体场与温度场的计算，并对冷却器进行优化，改善了冷却性能。文献[6]确定了气隙的导热系数及各部件散热系数，并讨论了负载、散热翅高度及铸铜对温度的影响。文献[7]采用流-固共轭传热数值计算方法对永磁同步电机的散热性能进行了仿真计算,得到了不同工况下电机定转子的温度分布规律。文献[8-9]建立含有水路的电机仿真模型，基于流固耦合传热理论，分析了电机在水冷方式下的电机温度分布。由于大中型电机功率大、发热密度高，目前许多大中型电机采用水冷散热或冷却管道散热的方式控制电机温升，散热能力强但结构复杂，维护成本高。紧凑型自扇冷式电机仅采用自带风扇冷却，冷却能力较以上方式弱。为准确计算流体场和温度场，对电机和内、外风扇装置建模并进行流热分析。

本文以Y2-500-6型紧凑型高压异步电机为例，建立电机的电磁有限元计算模型，计算出电机的定转子损耗；建立电机本体及电机内外流体场的三维有限元模型，采用多参考坐标系模拟风扇的旋转，为空气流动提供动力。将电机损耗折算为热源，通过流体场与温度场耦合计算，得出电机在内、外双风扇冷却作用下的流体场和三维全域温度场。比较了电机在有、无内风扇作用的情况下定转子温度值的差异。

1 电机基本参数及模型

本文所研究的电机为Y2-500-6紧凑高压型三相异步电机，其定子绕组采用星型连接，转子为铸铝鼠笼式结构。电机参数如表1所示。

表1 电机参数

电机的三维结构模型如图1所示。由于电机实际结构较为复杂，在建模过程中进行了适当简化，将端盖与机壳合并为一个整体。

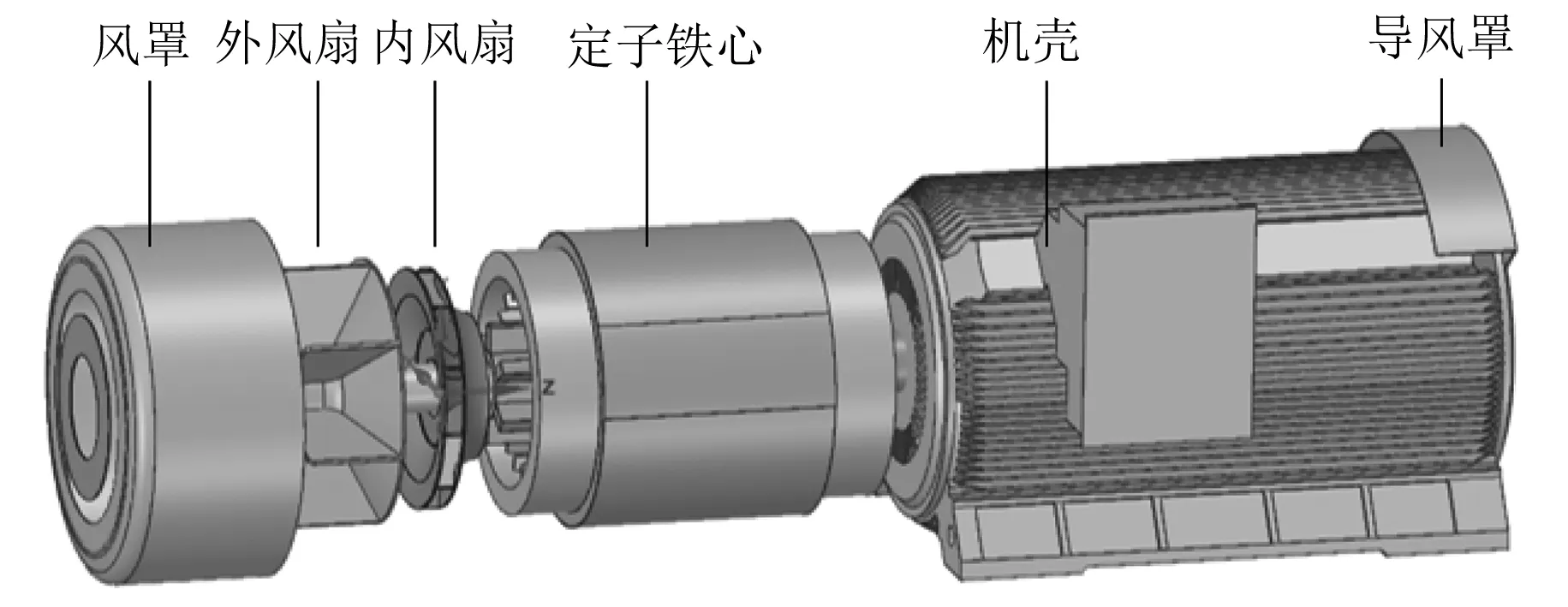
图1 电机三维结构模型

2 电磁计算

2.1 电磁有限元仿真计算

依据电机结构参数，在Maxwell电磁仿真软件中建立电机二维计算模型。转轴部位磁密小，对计算结果的影响可以忽略，为方便计算对转轴进行了简化。通过仿真计算，可以得到电机在10 kV、450 kW额定负载工况下运行时的磁通密度分布，如图2所示。

图2 磁通密度分布

由图2可以看出，磁通密度在铁心上呈周期性分布且最大值位于转子槽顶部。

2.2 铁心损耗

铁耗是电机损耗的重要组成部分。对于三相异步电机铁耗，目前比较常用的是三项式计算，铁耗PFe计算表达式为[10]

PFe=Ph+Pc+Pe=

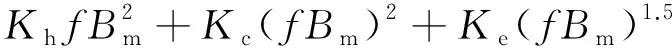
(1)

式中：Ph为磁滞损耗；Pc为涡流损耗；Pe为异常损耗；Bm为磁通密度幅值；Kh、Kc、Ke分别为磁滞损耗系数、涡流损耗系数和异常损耗系数；f为磁场交变频率。

通过Maxwell瞬态电磁场仿真得到的铁心损耗随时间变化曲线，计算得出额定工况下稳定运行时的铁耗约为4.764 kW。

2.3 绕组铜耗

在计算电机铜耗时，考虑电机定子绕组为线式绕组，不包含集肤效应，铜导线温度场均匀加载。电机绕组铜耗PCu计算公式为

PCu=3I2R

(2)

式中：I为绕组相电流有效值；R为绕组相电阻。

定子铜耗通过定子相电流和绕组相电阻计算得到，额定工况下稳定运行时的铜损为6.596 kW。

2.4 机械损耗

异步电机的机械损耗Pfw一般采用以下公式计算：

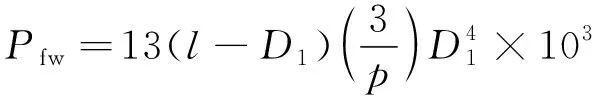
(3)

式中：p为电机极对数；D1为电机定子外径。

3 数学模型

3.1 求解方程

3.1.1 流体流动控制方程

电机内的流体流动受物理守恒定律的支配，在流动过程中同时满足质量守恒定律、动量守恒定律和能量守恒定律，其中能量守恒定律体现了流体系统的热交换。可以通过控制方程描述这些守恒定律。方程具体如下：

(4)

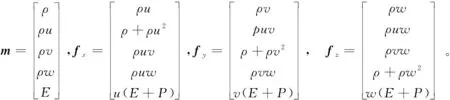
式中：ρ为密度；t为时间；u、v、w分别为x、y、z方向的速度分量；E为每一单位容量所含总能量；P为压力。

3.1.2 传热方程

根据传热学的基本理论，在直角坐标系下，电机额定负载运行时，求解域内三维稳态热传导方程有如下形式[11]：

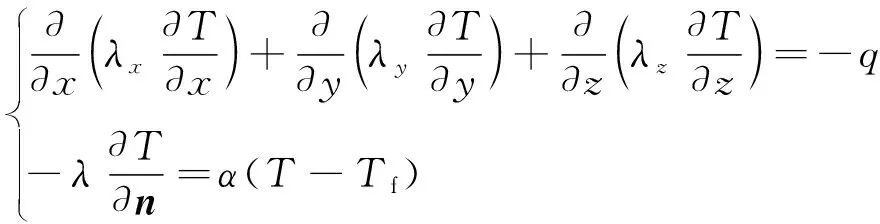
(5)

式中：T为温度；λx、λy、λz分别为x、y、z3个方向的导热系数；q为热源密度；n为表面单位法向矢量；α为散热系数；Tf为环境温度。

3.2 基本假设和边界条件

为确保模拟计算符合实际物理过程，作以下基本假设[12]：(1)电机内外空气流体的雷诺数很大，流动属于湍流，因此采用湍流模型求解；(2)由于电机周围流体流速小于声速，即马赫数很小，电机内外流体作为不可压缩流体；(3)风扇周围流体场属于旋转流体场，采用多重参考坐标系模型(MRF)模拟；(4)由于流体流速较快，可忽略流体域内流体的浮力和重力的影响。

本文研究电机在额定工况下的温度分布情况，因此对电机外流体场的风路入口和出口分别采用压力入口和压力出口边界条件，初值设为1个标准大气压，求解域内流体与固体的接触面均认为是无滑移边界。

3.3 通风结构

紧凑型异步电机采用全封闭自扇冷式结构，主要依靠机壳上的散热筋散热。全封闭自扇冷电机具有双冷却回路，即外部冷却与内部冷却。外部冷却主要由电机外风扇将空气吹向散热筋，从而进行机壳与空气的热交换；内部冷却主要由内风扇及转子自力性扇叶的转动将电机内部绕组、转子等部件的热量与空气进行热交换。内外风扇均采用风量大、效率高的离心式风扇，将流体从风扇的轴向吸入后利用离心力从圆周方向甩出，并配合风罩的约束将空气吹向散热筋。此外，在电机机壳内部轴向上设有4个通风槽，转轴设计为齿轮状，转轴凹槽与转子铁心构成转子通风沟，机壳内通风槽与转子通风沟共同构成电机的内部循环通道。电机转子通风沟结构如图3所示。

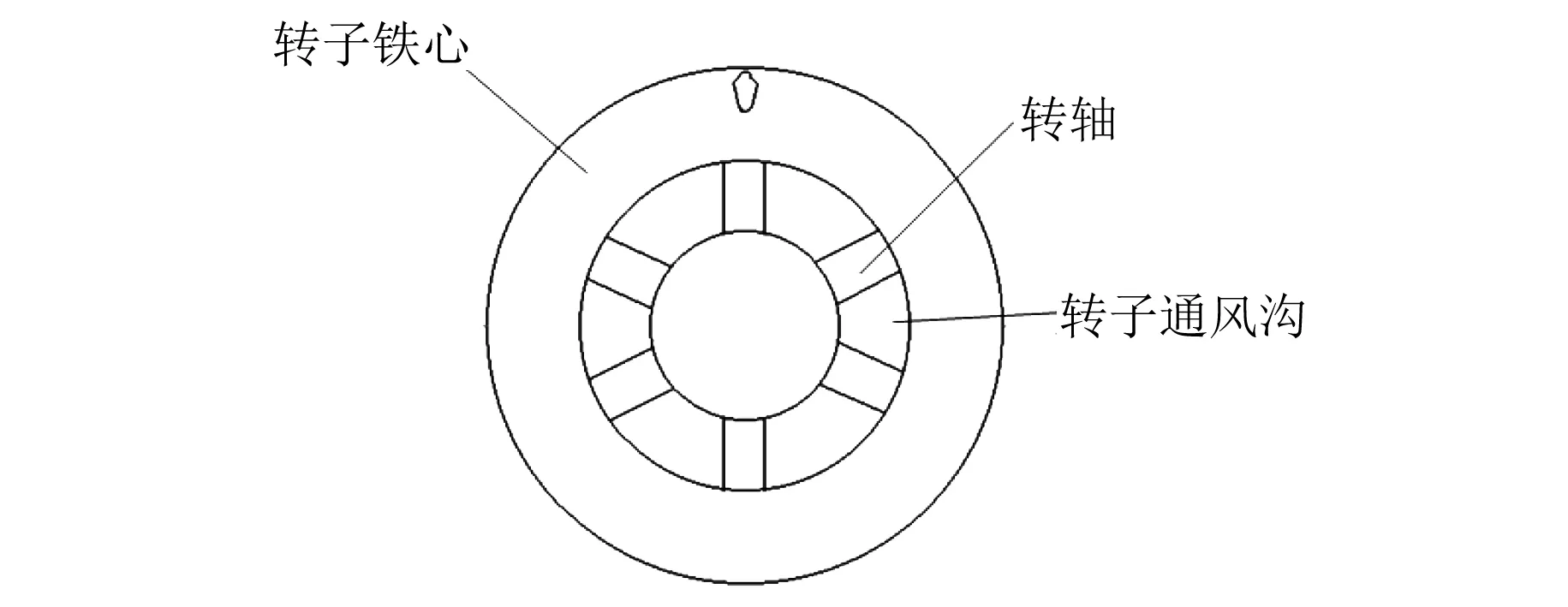
图3 转子通风沟

在对电机进行温度场的计算时，电机内温度的传递为热传导和热对流2种方式。在模拟热传导时需要确定电机各零部件材料的导热系数和比热容。本电机所用材料属性如表2所示。在模拟热对流时需要确定电机各零部件的散热系数。在以往的研究中散热系数大多由经验公式计算，本文采用流热耦合的方法可直接计算得到电机定子、转子、机壳、转轴等表面的散热系数。

表2 电机材料属性

4 计算结果分析

4.1 流体场计算

本文在电机的流体场计算中采用MRF模拟电机风扇的旋转，期望得到额定转速条件下内外风扇对电机流体场的作用以及对温度的影响。在风扇入口处设置压力入口边界，在轴伸端一侧设置压力出口边界。可计算得出电机内外流体场的分布情况。

图4为电机外风扇旋转情况下的机壳表面空气流迹图。由图4可知，空气从风罩涌入，在扇叶处旋转后沿着散热筋沟道流向机壳表面；空气在扇叶附近的流速明显高于其他位置的流速，靠近外风扇的散热筋内的空气平均流速约为30 m/s，靠近轴伸端的散热筋内的空气平均流速约为14 m/s。在电机轴伸端机壳上的导风罩改变了沿散热筋流动的气体的方向，使部分空气向下流动从而对轴承进行散热。

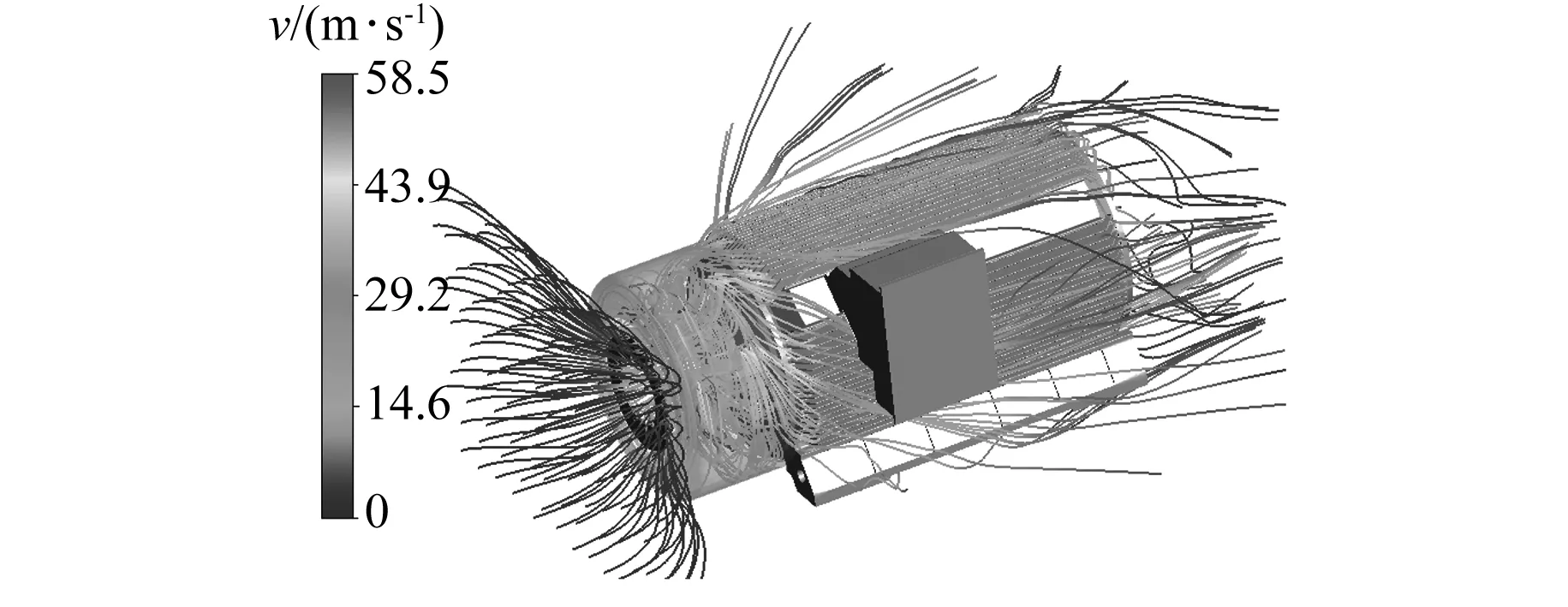
图4 机壳表面空气流迹图

图5为电机内流体场流速矢量图。由图5可以看出在内风扇及自力性扇叶作用下的空气流动状况：内风扇周围空气流速较高；空气通过机壳内通风槽流向轴伸端，再通过转子通风沟流回风扇端，构成封闭式通风循环流道，内部空气的循环流动使转子内部产生的热量传到机壳，降低转子温度；转子通风沟内空气流动方向由轴伸端流回风扇端，流速约为10 m/s。电机轴伸端的转轴上安装了与转子铁心外径相等的挡风板，阻挡绕组端部的部分气体，使端部绕组与气体换热更充分。

图5 电机内流体场流速矢量图

图6所示为气隙内气体沿轴向的流速。由图6可知，风扇侧流速明显高于轴伸侧；气隙两端有风扇作用且空间较为开阔，空气流速高，风扇端部气流流速达到10 m/s；气隙内由于受定转子结构影响空间变窄，空气流动平缓，速度维持在约4.5 m/s。

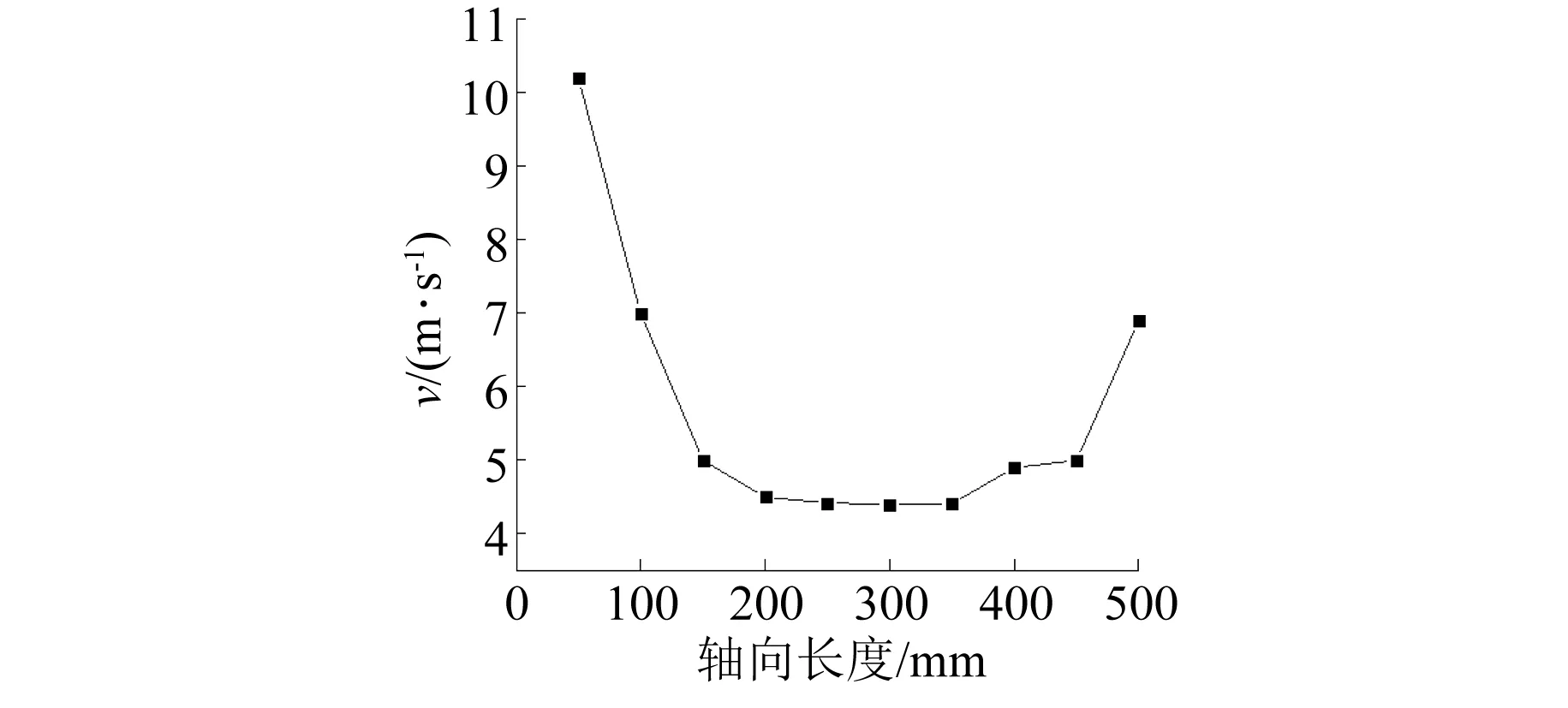
图6 气隙内气体沿轴向流速

图7所示为机壳表面散热系数分布，充分体现了流体场分布的连续性。由图7可以看出，机壳表面平均换热系数约为90 W/(m2·K)，最大约为150 W/(m2·K)；靠近风扇一侧机壳与空气的换热效果明显高于另一侧，沿着机壳轴向换热效果逐步降低，这是由于风扇一侧空气流速更高。

图7 机壳散热系数分布

4.2 温度计算

随着异步电机的运行，电机各部件不断产热，导致内部温度逐渐升高。内部产生的热量通过铁心与机壳之间的热传导、各部件与空气之间的热交换被转移到电机外部，最终电机的产热与散热达到动态平衡，电机温度不再改变。本文设定电机周围环境温度27 ℃，在额定电压10 kV、额定负载条件下，分别对电机有内风扇工作和无内风扇工作时的稳定运行温度场进行求解。

4.2.1 内风扇工作

图8所示为机壳温度分布。由图8可知，机壳中段与定子铁心紧密接触，导热效果好，定子铁心和定子绕组热量能迅速传递到机壳，机壳中段温度较高；定子绕组端部通过空气与机壳换热，导热效果较差，因此机壳两端温度较低；机壳径向上温度无明显差异。

图8 机壳温度分布

图9所示为内风扇工作时电机内部温度分布。由图9(a)和图9(b)可知，转子绕组中段的温度最高，达到147 ℃，转子绕组端部温度约为115 ℃；绕组径向上温度差异较小，而轴向上温度差异较明显；由于自力性扇叶的作用，绕组两端的温度低于导条中部的温度。

由图9(c)和图9(d)可知，定子绕组温度高于定子铁心，定子绕组中段温度高达113 ℃，靠近内风扇侧绕组端部温度较低，约为82 ℃；绕组端部受内部循环空气的影响，定子绕组轴向上的温度分布为中部高、两端低。

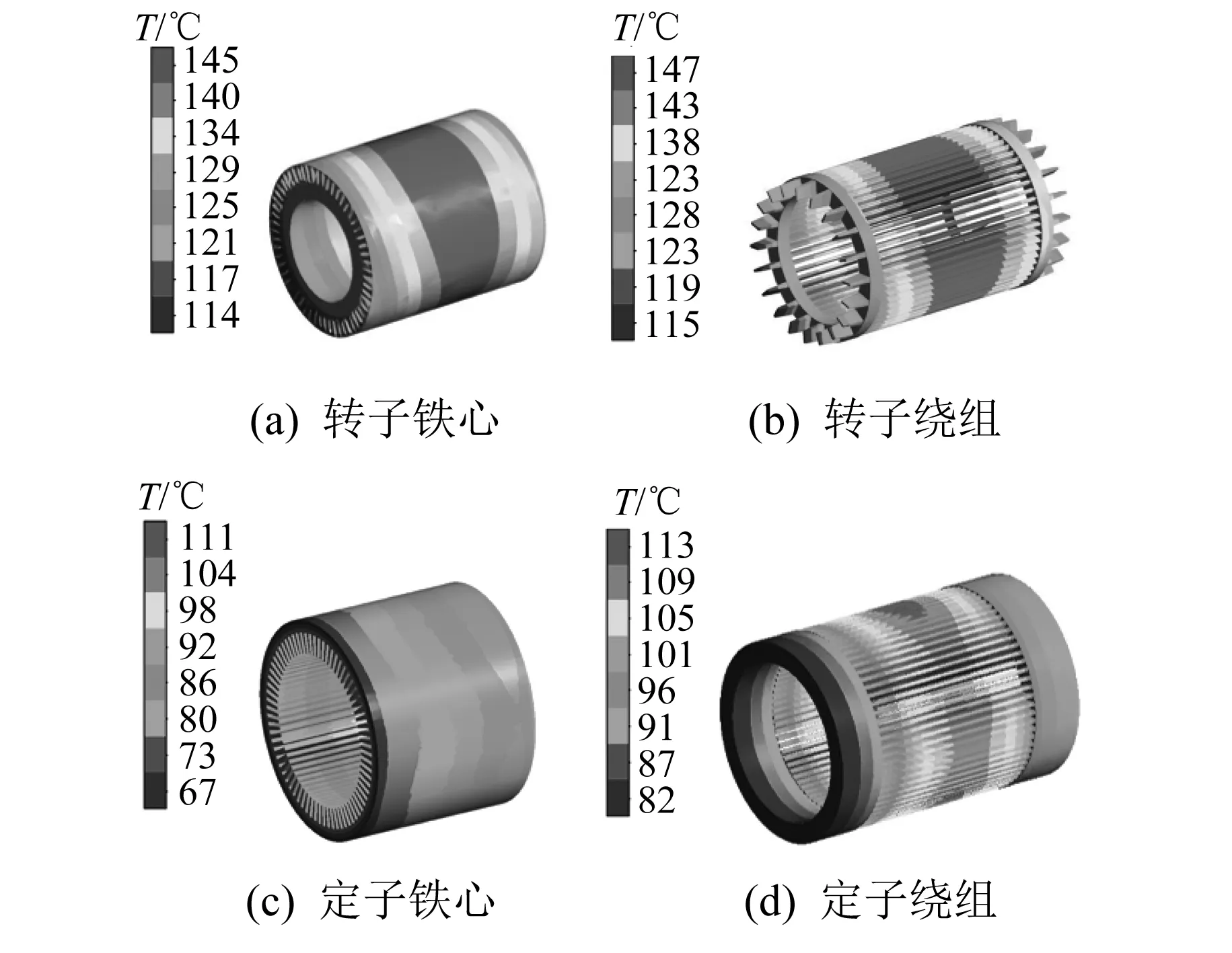
图9 内风扇工作时电机内部温度分布

4.2.2 内风扇不工作

将内风扇转速设为0，模拟外风扇单独作用下电机的散热情况，结果如图10所示。由图10(a)和图10(b)可知，当内风扇不工作时转子温度分布规律没有明显变化，但最高温度达155 ℃，转子端部绕组温度约为120 ℃，故内风扇不工作时转子温度整体有所上升。这是因为内风扇转动时将转子产生的热量通过转子通风沟带到机壳内通风槽，热空气在通风槽处与机壳进行热交换，然后流回转子通风沟。内风扇能够有效加强转子的散热能力。

由图10(c)和图10(d)可知，内风扇不工作时定子绕组温度分布为中部低、两端高，这是由于定子绕组端部与静止空气接触传热，散热效果低于与定子铁心接触的定子绕组中部，同时在外风扇作用下绕组两端温度出现差异。内风扇不工作时定子温度整体有所上升，最高温度达117 ℃。

图10 内风扇不工作时电机内部温度分布

5 结 语

本文以Y2-500-6紧凑型高压异步电机为研究对象，采用有限元法对样机进行了电磁场、三维全域流体场及温度场的仿真计算。通过电磁场有限元法准确计算了电机在额定工况下的铜耗和铁耗，为温度场计算提供热源。电机稳定运行时外部空气基本沿散热筋流动，空气流速沿轴向逐步降低，降幅约为53%。内风扇工作条件下的定、转子温度整体低于内风扇不工作条件下的温度。内风扇工作时，空气在气隙中的平均流速约为4.5 m/s，转子通风沟内的平均流速约为10 m/s。

转子上的温度整体高于定子温度；转子和定子温度沿轴向的分布均呈现中间高、两端低的特征；电机温度最大值位于转子绕组中部，为147 ℃，定子绕组温度最大值为113 ℃，满足F级绝缘的温度限值要求。