永磁辅助同步磁阻电机交直轴电感参数分析

肖 勇, 陈 彬, 李 霞, 史进飞, 王 杜, 李 莹

(1.广东省高速节能电机系统企业重点实验室,广东 珠海 519070；2.珠海格力电器股份有限公司，广东 珠海 519070)

0 引 言

永磁辅助同步磁阻电机[1-2]在转子内放置永磁体，电机的交直轴磁路不对称，由此产生的磁阻转矩能否得到充分的利用，与电机的交直轴电感参数密切相关。因此，在电机设计初期，通过仿真手段精确计算电机的交直轴电感参数具有重要意义。

目前，相关文献对永磁电机交直轴电感参数的计算和仿真方法进行了多方面研究。文献[3]在瞬态场中采用增量法计算得到了电机交直轴电感随电角度的变化曲线。文献[4-5]利用可计及电枢磁动势所产生的谐波漏感的绕组函数法量化分析了分数槽集中绕组永磁同步电机电感参数。文献[6]为减小有限元计算工作量，采用在特定转子位置下计算电枢绕组交直轴电感的方法。文献[7-8]采用静态场法分析了交直轴电感随交直轴电流的变化规律。文献[9]采用解析法通过公式推导分析了双绕组永磁同步电机不同嵌线方式对电感的影响。文献[10]采用集中参数法研究了饱和对永磁同步电机交轴电感的影响。文献[11]在非线性B-H数学模型的基础上，提出一种新的集总参数法，以评估内置式永磁同步电机的非线性磁行为。文献[12]在不同工况下采用保存相对磁导率不变的方法来计算交直轴自感及其交叉耦合电感参数。

本文以一台6.8 kW永磁辅助同步磁阻电机为研究对象，采用等效交直轴法、静态场法、瞬态场法和冻结磁导率法进行了电机交直轴电感参数的仿真计算；试制样机，并采用伏安法测试了电机电感参数，将仿真结果和实验结果进行对比，验证了各仿真方法的准确性。

1 电机模型

以一台6.8 kW的永磁辅助同步磁阻电机为研究对象，样机的有限元分析模型如图1所示。电机主要设计参数如表1所示。

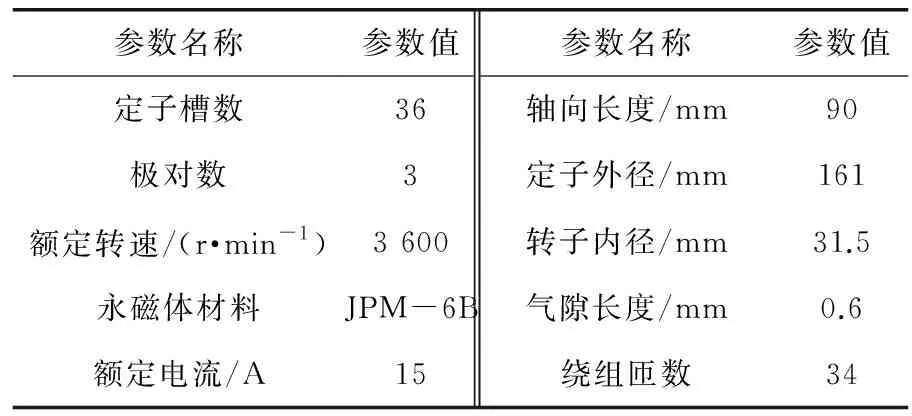
表1 电机参数

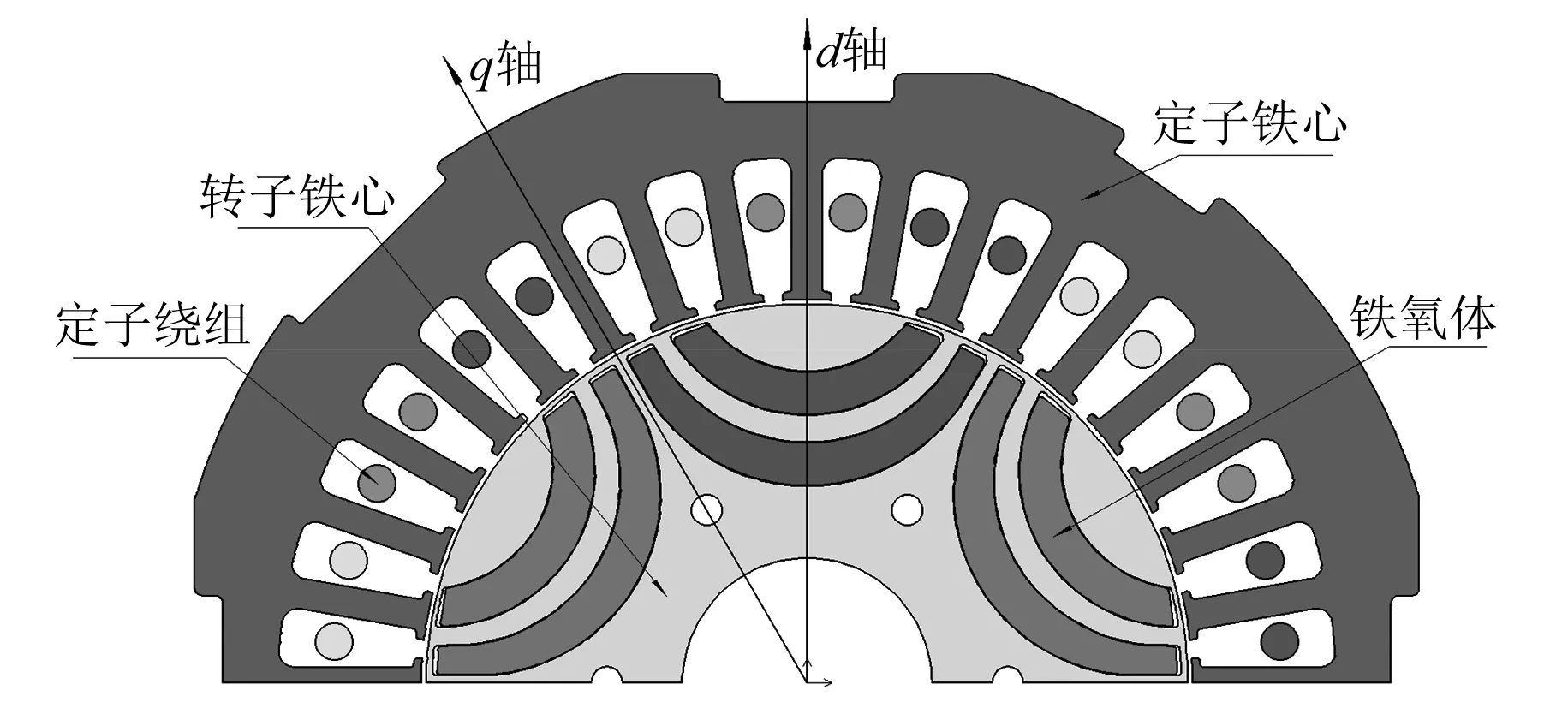
图1 电机模型

2 等效交直轴法

2.1 等效交直轴法的原理

等效交直轴法是将电机的运行状态分解为等

效直轴状态和等效交轴状态两种状态。等效直轴状态即定子磁场方向与转子磁场方向相同，此时直轴电感的计算公式为

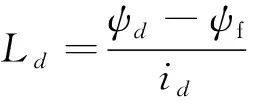
(1)

定子磁场方向与转子磁场方向垂直时即为等效交轴状态，此时交轴电感的计算公式为

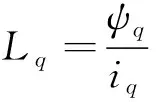
(2)

式中:Ld、Lq为直轴和交轴电感；ψd、ψq为直轴和交轴磁链；id、iq为直轴和交轴电流；ψf为永磁体磁链。

2.2 等效交直轴法的计算结果

采用等效交直轴法计算得到的不同电流下的交直轴电感如图2所示。额定电流下电机磁力线和磁密分布如图3所示。额定电流15 A时，Ld=3.48 mH，Lq=10.85 mH。

图3 额定电流下电机磁力线和磁密分布

随着电流的增大，电机饱和程度增加。由图2可知，交直轴电感值均随电流增大而减小，其中直轴电感从3.56 mH降至3.45 mH，下降幅度为3.15%；交轴电感从15.96 mH降至8.74 mH，下降幅度为45.22%。交轴电感的变化幅度大于直轴电感，交轴电感对电机的饱和更加敏感。

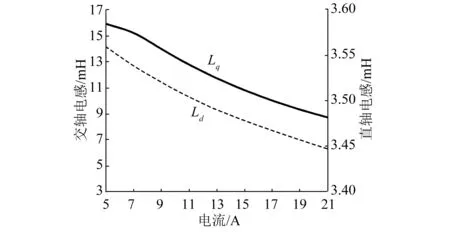
图2 等效交直轴法电感计算结果

采用等效交直轴法求得的交直轴电感是在弱磁角度为90°或270°以及180°状态下，绕组只有交轴磁场分量或直轴磁场分量，未考虑交直轴电流的交叉耦合作用对电感的影响。

3 静态场法

3.1 静态场法的原理

三相ABC坐标系下，电机的电感矩阵由三相绕组的自感及三相绕组之间的互感构成[13]，即：

(3)

要得到交直轴电感参数的计算公式，需将三相ABC坐标系下的电感矩阵变换到dq坐标系下，变换公式可由定子三相磁链的3s-2r变换得出：

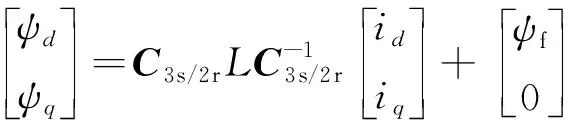
(4)

式中:C3s/2r为三相坐标到旋转正交坐标变换矩阵。

又因为在dq坐标系下有：

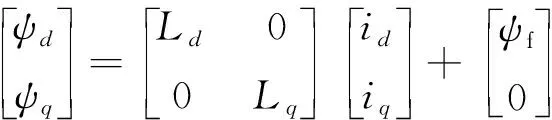
(5)

所以有：

(6)

由式(6)可得直交轴电感的计算公式为

式中:θ为直轴与A相绕组轴线之间的夹角。

3.2 静态场法的计算结果

采用静态场法计算得到的电机交直轴电感参数如图4所示。由图4可知，随着电流角的增大，直轴电感减小，交轴电感增大。在额定电流15 A下，交直轴电感的平均值Ld= 4.70 mH，Lq=14.46 mH。

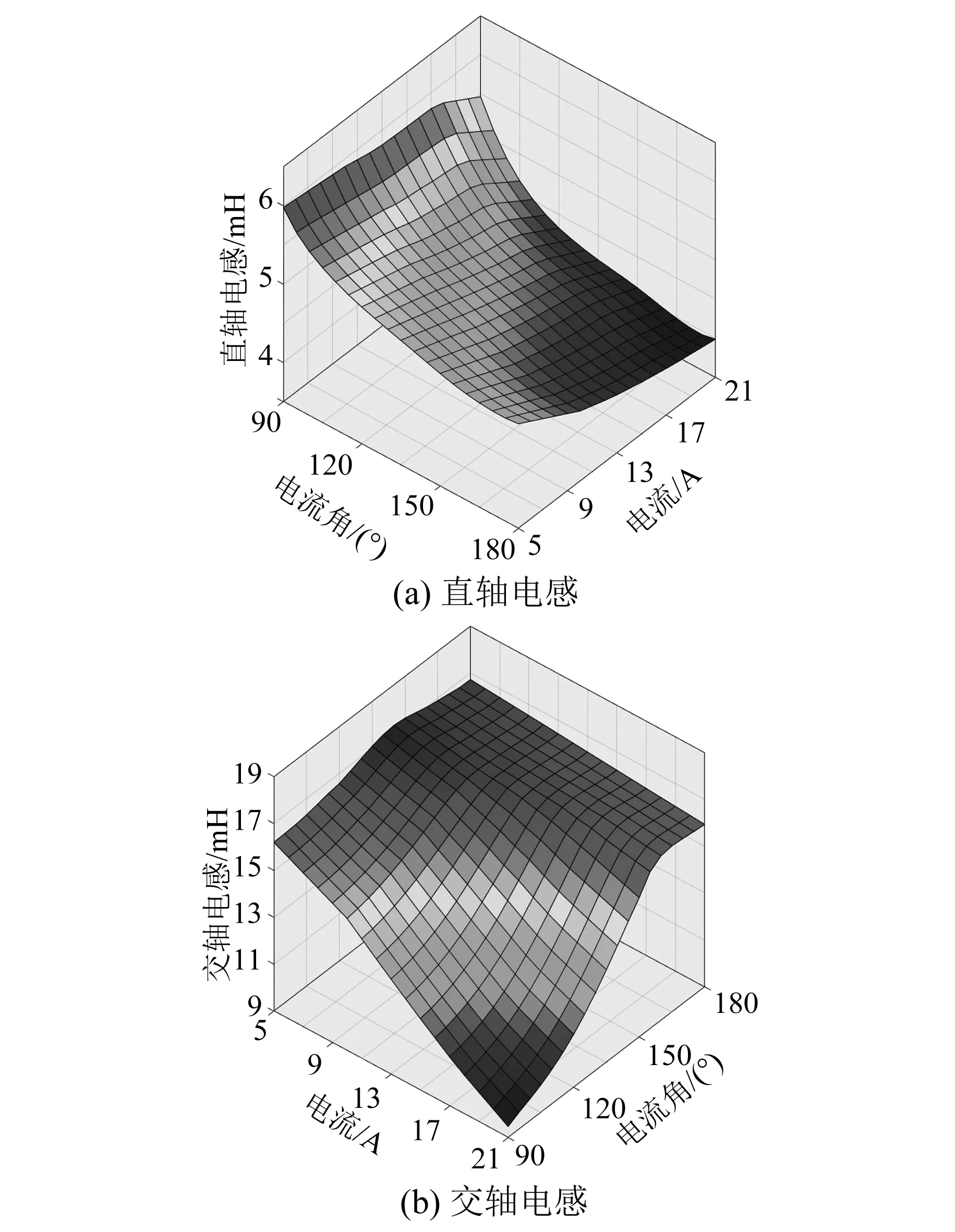
图4 静态场法电感计算结果

固定电流角，分析在只加载直轴电流和只加载交轴电流情况下，交直轴电感变化情况。只加载直轴电流时(电流角为180°)，随着电流的增大，直轴电感从4.84 mH降至3.99 mH，下降幅度为17.56%；交轴电感从16.71 mH降至15.93 mH，下降幅度为4.70%。可以发现，直轴电流的变化对直轴电感的影响更大。

只加载交轴电流时(电流角为90°)，随着电流的增大，直轴电感从5.98 mH降至5.46 mH，下降幅度为8.62%；交轴电感从16.2 mH降至9.47 mH，下降幅度为41.55%。可以发现，交轴电流的变化对交轴电感的影响更大。

4 瞬态场法

4.1 瞬态场法的原理

三相电流从ABC坐标到dq坐标的转换公式为

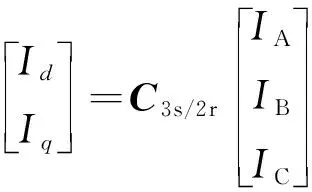
(9)

该公式对三相磁链也同样适用。

在瞬态场下，给三相绕组施加电流激励源，可计算得到电机的三相磁链值，经式(9)变换至dq坐标后得到电机的交直轴磁链和交直轴电流，按式(1)和式(2)可计算得到电机的交直轴电感值。

4.2 瞬态场法的计算结果

图5所示为瞬态场法计算得到的额定电流下电机交直轴电感结果。由图5可知，随着转子位置角的变化，交直轴电感均呈现周期性变化，其中直轴电感最大值为3.48 mH，最小值为3.25 mH，变化幅度为6.66%，取平均值为3.35 mH；交轴电感最大值为10.96 mH，最小值为10.62 mH，变化幅度为3.12%，取平均值为10.79 mH。不同电流下计算得到的交直轴电感值如表2所示。

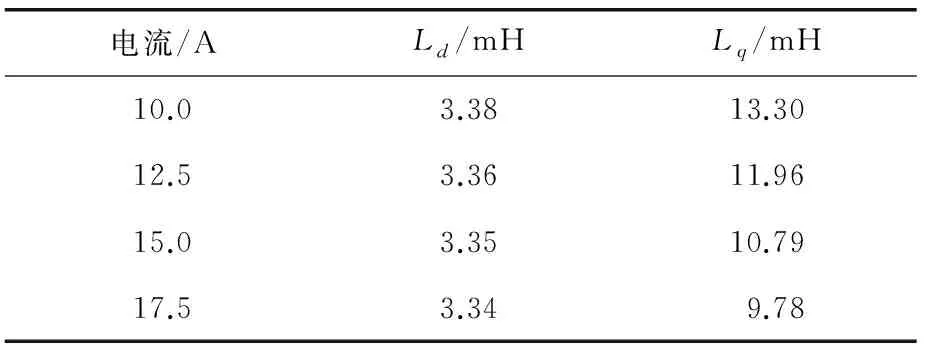
表2 不同电流下交直轴电感计算结果

图5 瞬态场法电感计算结果

5 冻结磁导率法

5.1 冻结磁导率法的原理

永磁辅助同步磁阻电机运行时，电机内存在由绕组产生的电枢磁场和永磁体产生的永磁磁场。传统磁链模型忽略了交直轴磁路间的交叉耦合作用与磁路饱和作用，认为交直轴磁场正交。为计及磁链交叉耦合作用和磁路饱和作用，永磁辅助同步磁阻电机的交直轴磁链可以表示为：

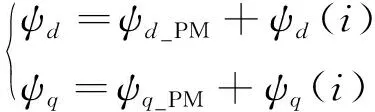
(10)

式中：ψd_PM、ψq_PM、ψd(i)、ψq(i)分别为永磁体和电枢电流产生的交直轴磁链。

根据式(10)可计算得到电机的交直轴电感，计算公式为

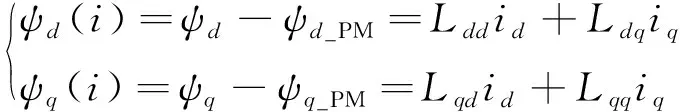
(11)

式中:Ldd、Lqq、id、iq分别为交直轴自感和电流；Ldq为交直轴互感。

根据式(11)计算电感参数考虑了交直轴磁路间的交叉耦合作用和磁路饱和作用，该方法需采用冻结磁导率技术[14-15]进行仿真。冻结磁导率技术的原理如图6所示，具体为：首先仿真负载磁场(A点)得到负载时的磁导率μall，并且将该值存储在各个单元的数据中；然后利用该磁导率分别分析只有永磁体激励的磁场B(FP,PM)(D点)和只有电流激励的磁场B(FP,i)(E点)，计算得到单独激励源下的磁链，进而计算得到交直轴电感。

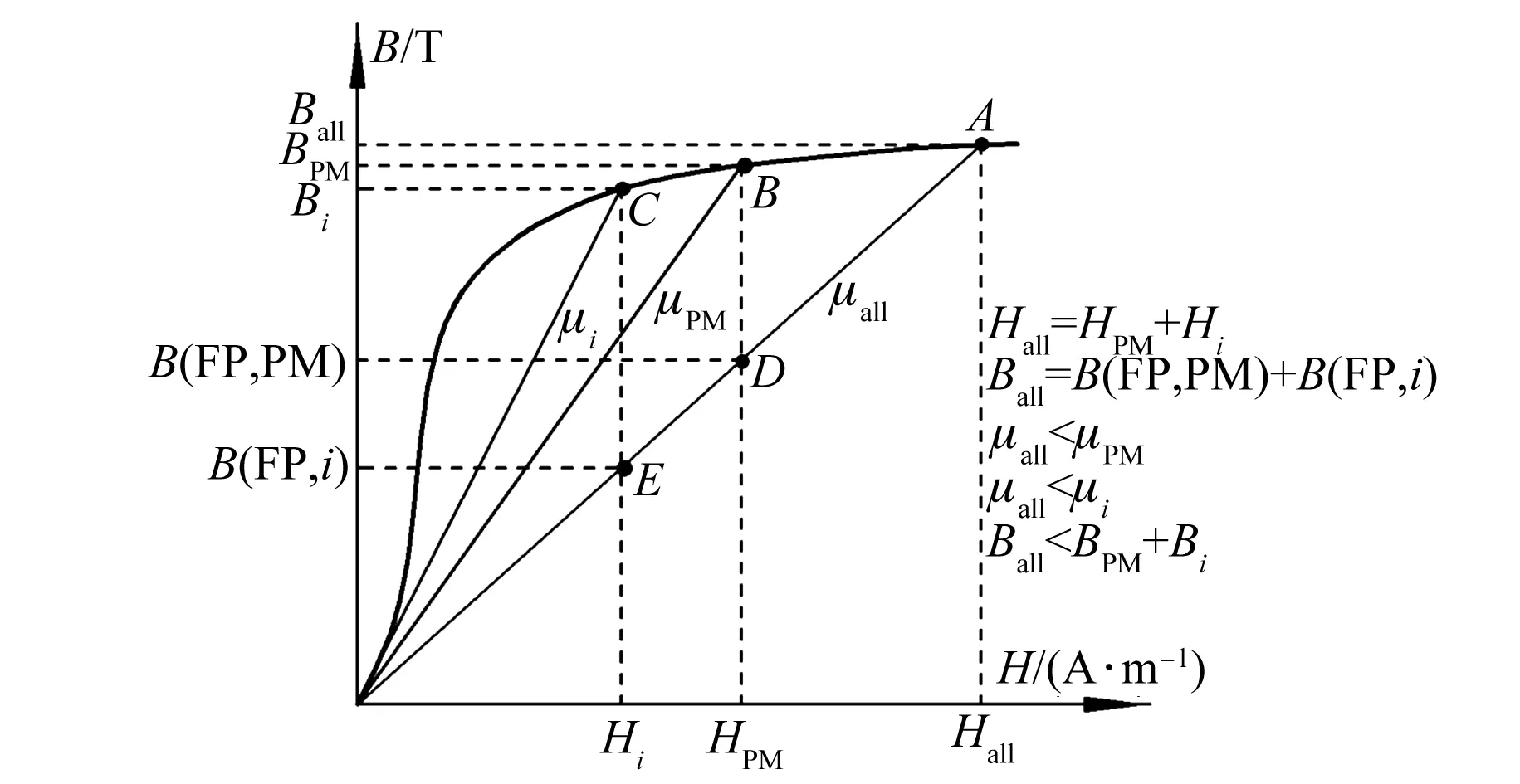
图6 冻结磁导率技术原理

5.2 冻结磁导率法的计算结果

图7所示为不同电流下电机相对磁导率云图，可见电机饱和程度受电流的影响比较大，尤其在定子上更为明显。图8所示为冻结磁导率法计算得到的不同电流下的交直轴电感。随着电流的增大，受电机饱和程度影响，交直轴电感随转子位置角的波动幅度增大。额定电流下的交直轴电感值Ld=3.78 mH，Lq=10.48 mH。

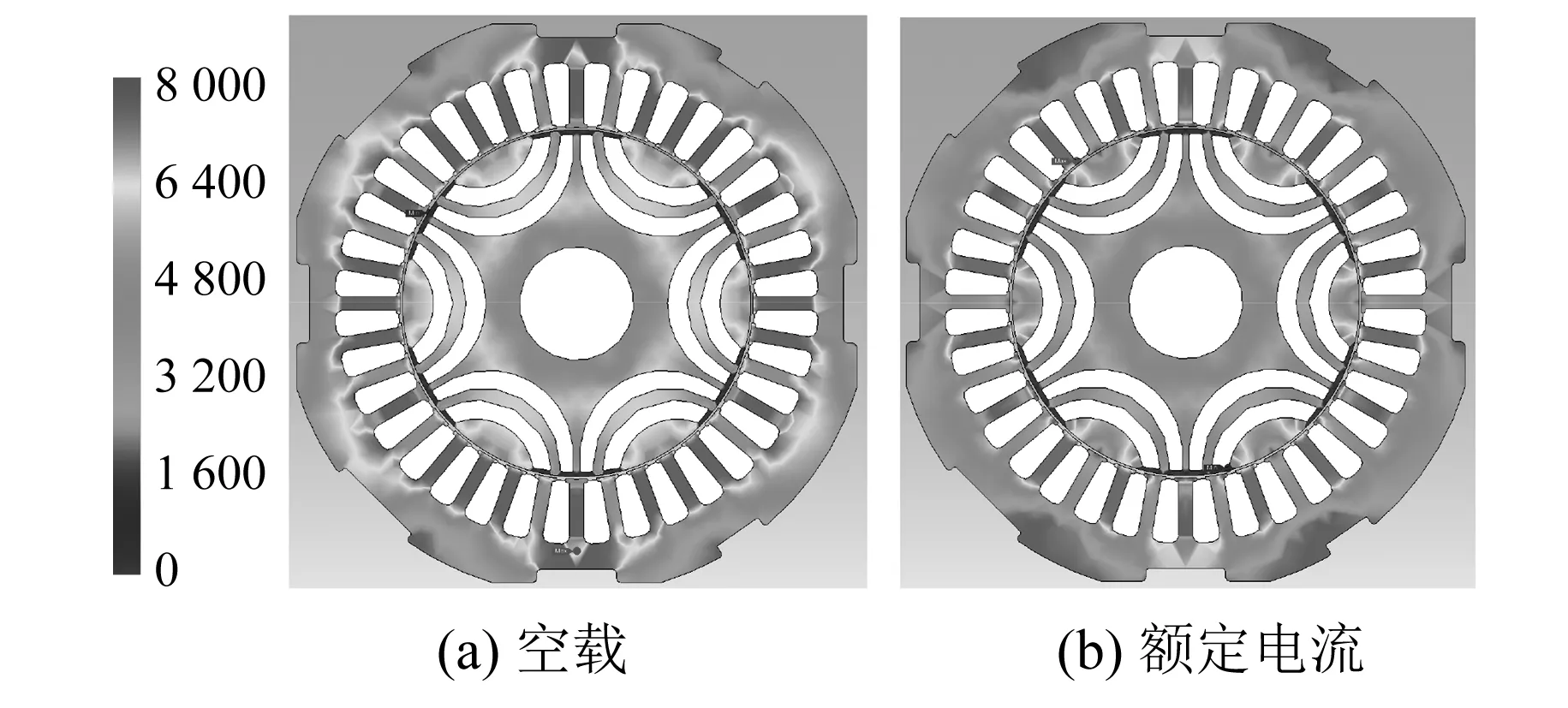
图7 不同电流下电机相对磁导率云图

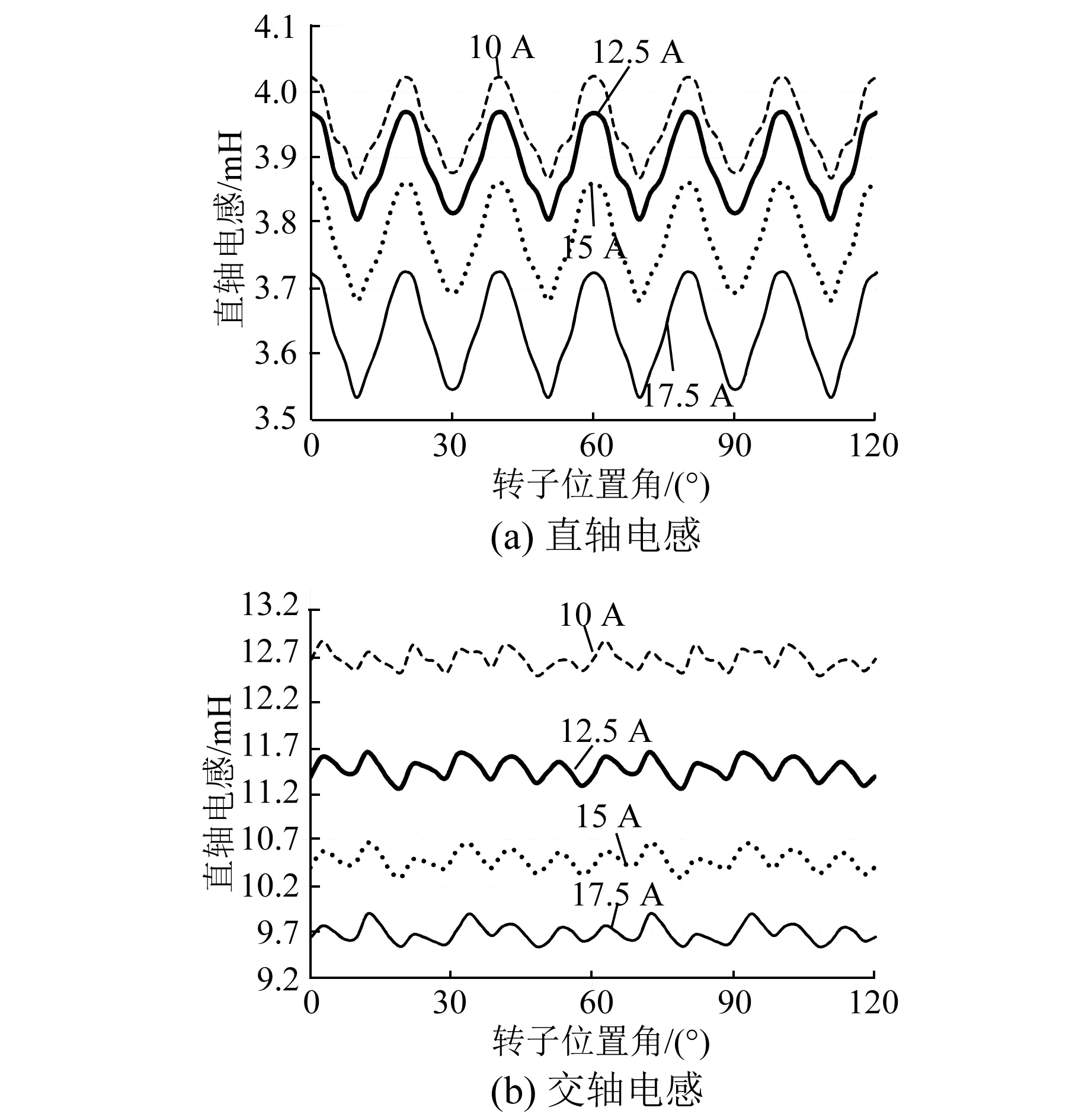
图8 冻结磁导率法电感计算结果

6 试验对比

试制样机并采用伏安法测试了样机电感参数。图9所示为样机定转子组件。将等效交直轴法、静态场法、瞬态场法和冻结磁导率法的计算结果与实测结果进行对比，误差如表3所示，其中冻结磁导率法计算结果与实测结果的误差最小，且电机饱和程度越高误差越小，采用冻结磁导率法的计算结果更为准确。

图9 样机定转子组件

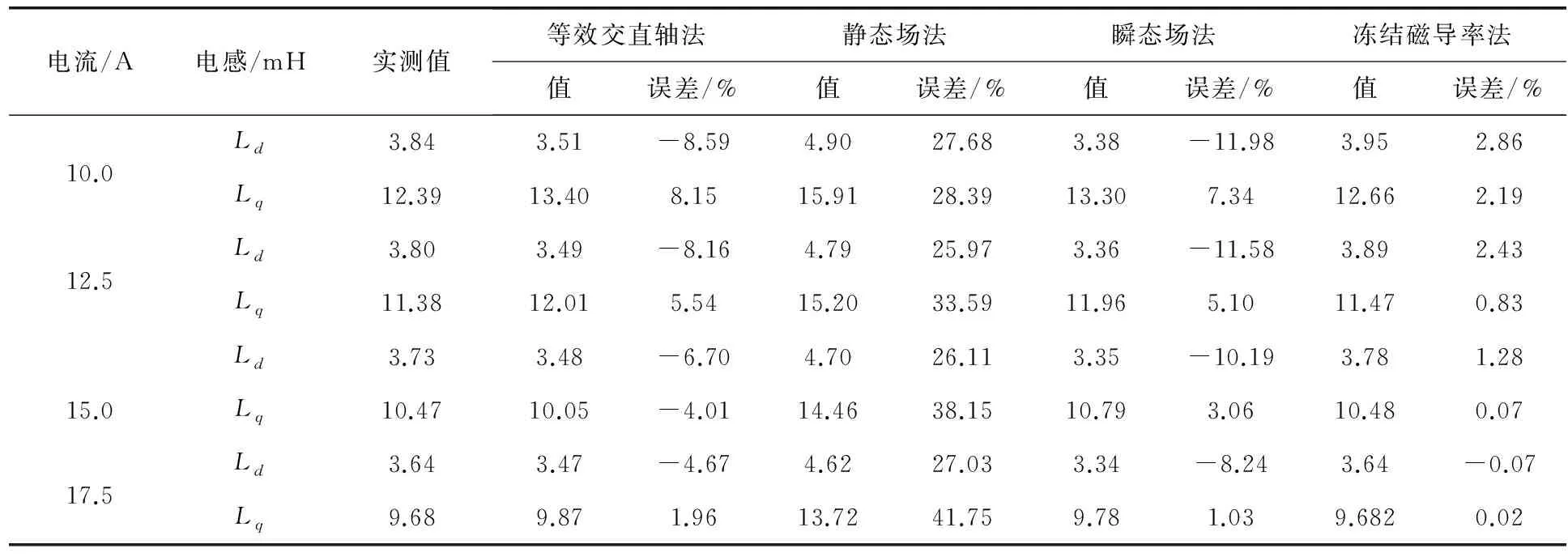
表3 交直轴电感计算结果对比

7 结 语

本文以一台6.8 kW的永磁辅助同步磁阻电机为研究对象，针对交直轴电感参数的仿真方法——等效交直轴法、静态场法、瞬态场法、冻结磁导率法，进行了原理介绍和结果对比，结论如下：

(1) 静态场法的计算结果与实测结果误差较大(25%以上)，该方法不可取。

(2) 等效交直轴法和瞬态场法的误差较静态场法小，且随着电流的增大，误差呈减小趋势；对比等效交直轴法和瞬态场法，采用等效交直轴法计算直轴电感的误差相对较小，采用瞬态场法计算交轴电感的误差相对较小。

(3) 冻结磁导率法计算结果与实测结果的误差最小且均在3%以内。采用冻结磁导率法计算交直轴电感参数更为可靠，且该方法更适合电机饱和程度较高时的电感计算。