高考指向核心素养，教学笃定立德树人——2020年全国理科一卷试题分析

■广东省广州市南沙麒麟中学 张志明

一、发展学生核心素养，培育时代创新人才

党的十八大明确指出：坚持教育为社会主义现代化建设服务、为人民服务，把立德树人作为教育的根本任务。2017 版新课程标准提出“高中数学课程以学生发展为本，落实立德树人这一根本任务，培育科学精神和创新意识，提升数学学科核心素养”。如今的数学教学现状是：数学概念从具体实例中抽象；问题分析在逻辑思维的细节里生成；形动数行有方向、数释形迹觅成因，运算与直观相辅相成；数学源于生活、解释生活现象、觅求生活规律、优化生活环境，建模便有了生命力；大数据、云计算、人工智能为数据分析提供了广阔的生长空间；核心素养的落实为培育新时代创新人才提供了充足的给养。

二、新高考为教学导向，新高考为学生素养“定妆”

2020 年高考的硝烟已散去，留下的是冷静的思索。新与旧的衔接处、过渡期，高考呈现出怎样的变化和规律？“穿新鞋走老路”是要平稳过渡，还是要锐意革新？新高考如何为教学导向，为素养定妆？这一系列的问题，我们都要从高考试题中找到答案。

（一）数无形时少直观，形缺数时难入微

2017 年全国一卷的太极图、2018 年的饼图、2019年的断臂维纳斯均为此类问题，尤其是“断臂维纳斯”的身高问题，许多同学深陷计算泥潭不能自拔。这类题目应当引起正在准备高考备考工作的教师的重视。

例1：（2020高考理科一卷第5题）某校一个课外学习小组为研究某作物种子的发芽率y和温度x（单位：°C）的关系，在20个不同的温度条件下进行种子发芽实验，由实验数据(xi,yi)(i= 1,2,L,20 )得到下面的散点图：

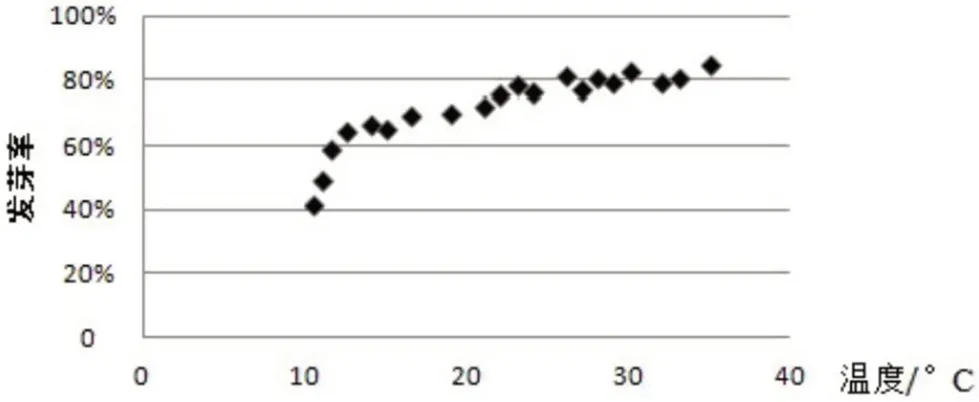
由此散点图，在10°C至 40°C之间，下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是（ ）。

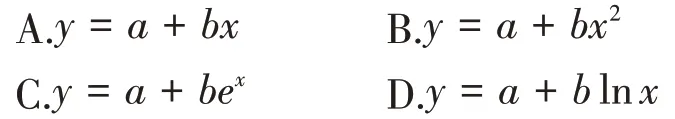
（二）训练算法算理，培养学生数学意识

1.算法讲算理，算中有逻辑。数学问题的特点是先运用思维逻辑思考，再进行精准计算，正所谓“方法好不好，计算为先导。”所以，高考的试题需要学生在计算和掌握算理上下功夫，培养自己的逻辑思维、数学运算等核心素养。

例2：（2020高考理科一卷第3题）埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为（ ）。

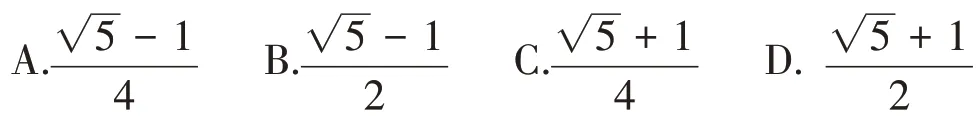
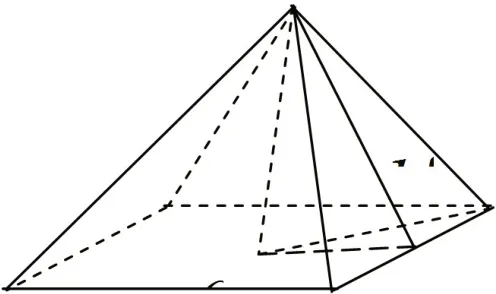
该题目的算法中蕴含方程思想、基本量思想，蕴含着高考对于算理的要求，考查学生的数学建模能力、运算能力、逻辑思维能力。

2.核心能力提素养，基本思想凝意识。学生核心素养的提升的表征为其数学意识的精进，而学生的数学意识通常是指数字意识、范围意识、几何意识、空间意识、概率和统计意识、应用和创新意识等，教师可通过强化学生的数学意识，增强学生的数学判断能力、分析解决问题的能力。

例3，（2020 高考理科一卷第7 题）设函数f( )x=在[- π,π ]的图像大致如下图，则f(x)的最小正周期为（ ）。

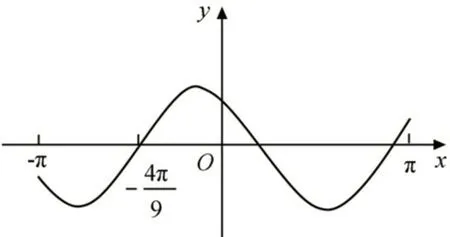
分析：本题考查学生对于三角函数图像和性质的理解，以及迁移应用的能力。

解法1：有图像可知：1 ＜ω＜ 2。

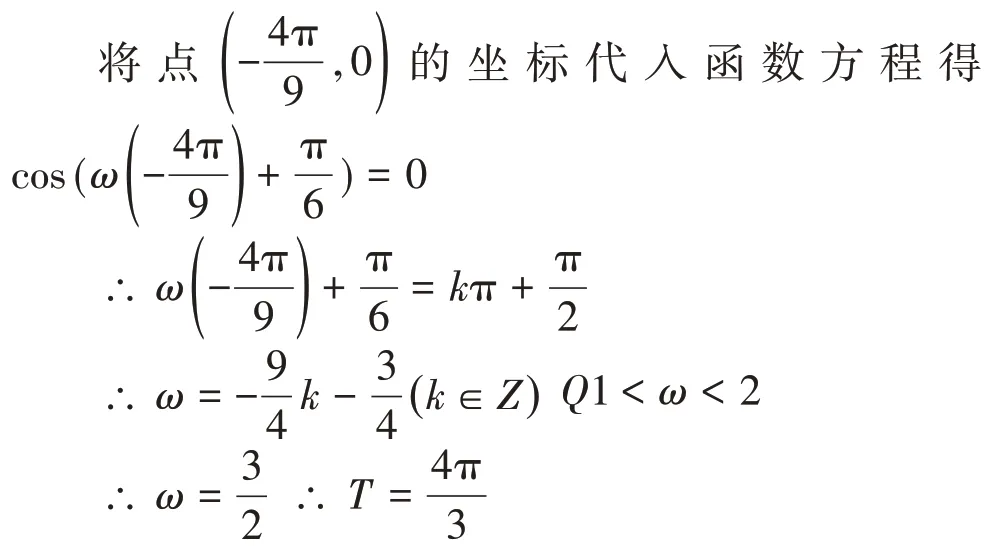
“提升核心素养，服务立德树人”这一核心理念做出了“学为本、教为辅”“学生为主体、教师为主导”的必然选择。因此，在今后的数学教学中，教师需全面了解学生，基于学生的学习现状和考题的变化，给予学生正确的教学指导。