基于拉压不同模量弹性理论的子午线轮胎有限元分析
冷国阳,陆 静,2,赵长松,马迎松,4*
(1.广西科技大学 机械与交通工程学院,广西 柳州 545006;2.广西汽车零部件与整车技术重点实验室,广西 柳州 545006;3.赛轮集团股份有限公司,山东 青岛 266500;4.广西汽车集团有限公司,广西 柳州 545007)
在汽车行驶过程中,轮胎与路面的接触部分承载各种路况条件下轮胎与地面之间的负荷转换,因此轮胎与地面的接触问题对汽车的安全性有重要影响,对轮胎进行受力分析是汽车性能研究的一个重要内容[1]。轮胎是汽车与地面接触的唯一部件,其所产生的滚动阻力对汽车燃油消耗有直接影响[2]。由于轮胎的接触问题非常复杂,利用仿真分析方法预测轮胎滚动阻力已经成为轮胎研发过程中的重要手段[3],未来轮胎的设计和研究都会以轮胎数据库为基础,仿真技术将更广泛地应用到轮胎设计和生产的各个方面,这也是当今大数据时代下轮胎设计与发展的必然趋势[4-6]。
子午线轮胎是主要由胎面、带束层、胎体、胎圈和胎侧组成的结构复杂的柔性层合体[7]。带束层是子午线轮胎的关键受力部件,承受65%左右的轮胎应力,通常采用纤维或钢丝帘线骨架材料,主要承受轮胎滚动时的周向应力作用[8]。目前,在轮胎有限元分析中通常认为带束层材料在受拉和受压时呈现相同的弹性性质。大量试验和研究表明,钢丝帘线材料在绝对值相同的拉应力或压应力作用下,会发生绝对值不同的拉应变和压应变,即材料具有拉压不同模量的非线性特性[9]。因此,将其视为各向同性均质材料是对材料非线性的一种简化,这种简化对轮胎有限元分析的准确性有较大影响。
本工作基于拉压不同模量弹性理论,发展并建立了高效、稳定的各向同性及拉压不同模量材料的计算框架,并通过UPFs(User Programmable Features)编译了拉压不同模量材料的用户子程序ANSYS.exe,对ANSYS软件进行二次开发。在此基础上,以215/65R16轮胎参数为参考依据,将带束层材料视为各向同性均质材料,建立子午线轮胎三维有限元模型,对轮胎进行充气和越障滚动工况仿真分析,研究胎内气体体积与压力的变化,为预测轮胎滚动阻力提供参考。同时,将带束层材料设置为不同的拉伸弹性模量与压缩弹性模量,进行相同工况的数值计算。通过两种数值模型分析对比,研究帘线材料的拉压不同弹性模量性质对轮胎力学特性的影响。
1 拉压不同模量弹性理论
C.A.阿姆巴尔楚米扬[10]认为,不同模量弹性理论是指符合连续弹性介质力学基本原理的不同模量物理理论,其建立依据是连续弹性变形体力学原理,虽然在整体上没有内在的矛盾,但是却存在至今未解释清楚的原理以及未被证明的定理,这些都是亟待解决的问题。拉压不同模量是指在绝对值相同的拉应力或压应力作用下,材料会发生绝对值不同的拉应变和压应变[11]。当材料受轴向作用力时,其应力与应变的关系呈双线性,即具有拉伸弹性模量与压缩弹性模量不同的性质。简单的双直线模型的本构关系如图1所示,图1(a)所示为真实情况,图1(b)和(c)所示则是抽象后的双直线模型,其中材料拉伸时的弹性模量和泊松比分别为E+和μ+,材料压缩时的弹性模量和泊松比分别为E-和μ-,σ为应力,ε为应变。
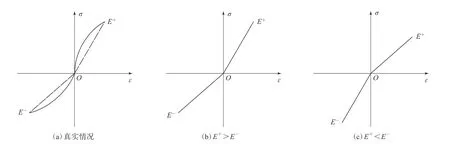
图1 不同模量材料的本构关系(双直线模型)
双直线模型实际上是将σ分为2个区段(σ≥0和σ≤0),对应力与应变的非线性关系用相应的线性关系来近似表征,即对具有不同拉压弹性模量的材料用双直线模型来确定其受拉和受压关系,这是有足够精度的一种近似方法。但是由图1可以发现,图1(a)曲线在坐标轴原点处是连续的,而图1(b)和(c)曲线在坐标轴原点处的切线是不连续的。实际上,用分段直线函数表示应力与应变之间的关系并非如此简单。
随着主应力在给定点上的正负号不同,具有拉压不同弹性模量材料在相应方向上会表现出不同的弹性性质,由主应力描述的本构方程[12]为
式中,σi和εi(i=1,2,3)分别为3个主应力和主应变。弹性模量(Ei)和泊松比(μi)的正负性质由对应的主应力确定,即若σi≥0,则Ei=E+,μi=μ+;反之,则Ei=E-,μi=μ-。
2 轮胎数值计算模型
以215/65R16轻型载重子午线轮胎为例,通过简化,将轮胎分为胎体、带束层、胎侧和轮辋四部分来建立子午线轮胎三维数值模型,对轮胎进行充气和越障滚动工况仿真分析。
2.1 轮胎有限元模型
轮胎的胎体采用SOLID186实体单元建模,如图2所示。轮胎内部采用HSFLD242流体静力学单元,在单元上使用一个压力节点ID来包围空气,如图3所示。
图3 轮胎内部空气模型
轮胎的骨架材料使用Reinf265单元建模,采用不同的材料模型分别定义带束层和胎体层的骨架材料,如图4和5所示。

图4 轮胎与路面接触面的增强帘线层(带束层)
轮辋使用多点约束算法(刚性约束)建立刚体模型,轮辋与轮胎的接触采用刚-柔接触模型进行模拟。采用Conta175单元定义轮辋节点与胎圈的接触,轮辋与胎圈为多点刚性曲面约束。
图5 胎侧部位的增强帘线层(胎体层)
轮胎与路面之间的面与面接触对模型如图6所示。轮胎与路面的接触面使用Conta174单元定义,路面为目标面,使用Targe170单元定义。

图6 轮胎与路面之间的面与面接触对模型
通过定义轮胎轴心节点(1026),使用Mass21质量单元进行汽车质量的定义。
2.2 本构模型及材料参数
根据橡胶材料的不可压缩性,采用Mooney-Rivlin双参数模型,其应变能函数(W)展开式为
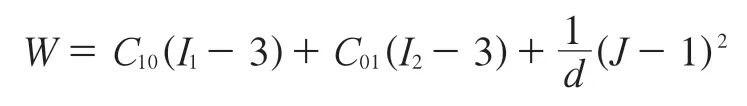
式中,I1和I2分别为第一和第二应变偏量不变量;C10和C01为橡胶材料系数;d为材料不可压缩参数,对于不可压缩材料,J=1。
材料的初始切变模量为2(C10+C01),初始体积模量为2/d,d=(1-2μ)/(C10+C01),计算得到C10和C01分别为0.551 584和0.137 896 MPa,d为0。
橡胶材料的基本参数为:弹性模量 6 894.8 MPa,泊松比 0.5,密度 2.76 Mg·m-3。
轮胎内部空气采用HSFLD242流体静压单元进行模拟,在实体单元节点上施加压力用以封闭空气,是可压缩气体,其初始参数为:密度0.001 225 Mg·m-3,参考温度 20 ℃。
为了模拟帘线材料具有拉压不同弹性模量的性质,通过运行自编程的ANSYS.exe程序,分别设定帘线拉伸和压缩的弹性模量(E+,E-)以及泊松比(μ+,μ-)。由于至今尚无测量帘线压缩模量的正确方法,因此假定压缩模量为拉伸模量的1/10[13]。根据文献[14]可知,对于具有拉压不同弹性模量力学特性的材料,E+/E-=μ+/μ-近似成立,由此可以确定材料的泊松比。通过运行编写程序ANSYS.exe可完成对材料参数的设置。
带束层增强材料的基本参数为:E+2×105MPa,E-2×104MPa,μ+0.3,μ-0.03。
胎体层增强材料的基本参数为:E+2×104MPa,E-2×103MPa,μ+0.3,μ-0.03。
2.3 轮胎工况与边界条件
对轮胎模型进行数值分析时,为达到对轮胎负荷步求解的目的,加载共分为5步,具体边界条件与加载方式如下。
(1)全约束耦合轮胎轴中心的节点,在Y方向的重力加速度为9.81 m·s-2,设置轮胎的初始温度为20 ℃,模拟轮胎承受自然重力下的状况。
(2)通过施加压力边界条件来约束压力节点,给轮胎充气至0.248 MPa,模拟轮胎充气过程。
(3)将耦合轮胎轴中心的节点沿-Y方向移动50 mm,使轮胎与地面充分接触。
(4)释放耦合轮胎轴中心的节点位移边界条件,只使用MASS21单元来模拟轮胎承受车身压力的情况,车身分压到单个轮胎的质量为1 000 kg。
(5)在耦合轮胎轴中心的节点施加水平方向(Z方向)的加速度(1.4 m·s-2),进行瞬态分析,模拟车辆前进时轮胎的滚动过程。
在轮胎模型的5步加载分析中,负荷步1—4均为静态加载分析,负荷步5为瞬态分析。分析轮胎与道路的接触应力时,既要考虑轮胎运动、变形对与路面接触状态以及接触界面的影响,还要考虑外负荷对接触面积和接触压力分布的影响,因此采取直接约束法对轮胎与路面接触问题进行分析求解,通过直接约束法追踪轮胎的运动轨迹,当轮胎与路面接触时,将接触所需要的运动约束与节点力作为边界条件直接施加在产生的节点上,最后利用接触迭代算法分析轮胎与路面的接触问题。在分析胎内流体变化时采用HHT时间积分法进行非线性瞬态分析,实时监测胎内气体的变化情况。
3 结果与讨论
3.1 轮胎充气-静负荷分析
轮胎有限元分析包含几何非线性、材料非线性和边界条件的非线性[15-16]。轮胎在充气时,胎体受内部气压作用向外膨胀,胎体所受的应力与其所发生的应变呈非线性关系。采用经典各向同性弹性理论和拉压不同模量弹性理论对轮胎模型静载工况进行模拟分析。
轮胎模型在标准充气压力下胎内气体在Y方向(垂向)的位移云图如图7所示,轮胎的充气半径增大均约为5 mm。

图7 标准充气压力下轮胎垂向位移分析结果
轮胎加载向下移动50 mm,并对Y方向进行约束,胎面与路面接触压力分布云图如图8所示,接地印痕形状近似为矩形,最大接触压力均约为0.24 MPa。

图8 加载后胎面与路面接触压力分析结果
加载后轮胎横向位移云图如图9所示。轮胎与地面发生接触后,接地区域胎侧部位凸起,横向位移出现最大值,均约为22.0 mm。

图9 加载后轮胎横向位移分析结果
由于在充气和静态加载工况下轮胎是静止的,胎体受胎内气压作用处于拉伸状态,没有压应力存在,因此帘线所具有的拉压不同模量性质对分析结果没有影响,两种理论模型的分析结果是一致的。
3.2 轮胎滚动工况分析
在对轮胎滚动工况进行研究时,首先要激活瞬态分析,采用大变形方式。在静负荷工况基础上,车辆以1.4 m·s-2的加速度向前行驶,每个轮胎承载1 000 kg。在对轮胎施加加速度后,轮胎进行越障行驶,检测越障时胎内气压的变化。
在整个分析过程中,胎内气体体积的变化可从侧面反映轮胎的变形情况。在负荷步2时给轮胎充气,胎内气体体积达到最大;在进行越障时,轮胎受力变形,致使胎内气体体积变为最小;越过障碍时,轮胎变形程度减小,胎内气体体积又有所增大。
胎内气体压力在负荷步2后达到相对稳定状态;在负荷步4消除所有的自由度约束与压力边界条件,由于所受负荷的作用,轮胎的变形增大,气体体积减小,胎内气体压力增大;在越障时,由于轮胎变形,轮胎的体积减小,胎内气压增大。
胎内气体体积由轮胎模型给定,运行负荷步时质量恒定,其加载后预期的压力、密度和质量计算如下:
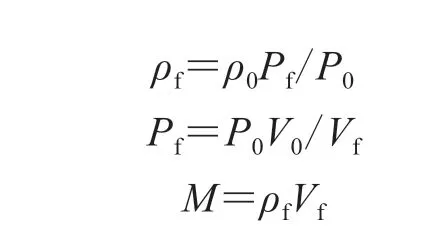
式中,ρ0和ρf分别为充气后和加载后胎内气体密度,P0和Pf分别为充气后和加载后胎内气体压力,V0和Vf分别为充气后和加载后胎内气体体积,M为胎内气体质量。
轮胎不同负荷下胎内气体压力、体积、密度和质量的计算与仿真结果如图10所示。
从图10可以看出,仿真结果与计算结果几乎相同,进而验证了使用流体静力学HSFLD242单元来模拟胎内气体的可行性。
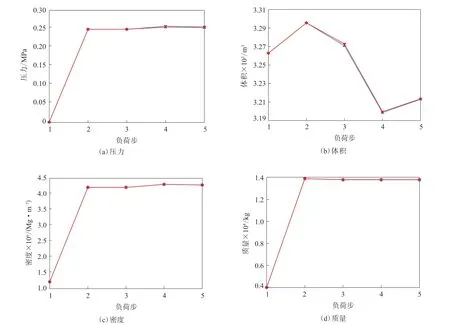
图10 不同负荷下胎内气体压力、体积、密度和质量的计算与仿真结果
滚动工况下,经典各向同性弹性理论轮胎模型和拉压不同模量弹性理论轮胎模型等效应力分布如图11所示。
从图11可以看出,经典各向同性弹性理论轮胎模型的最大等效应力为46.7 MPa,拉压不同模量弹性理论轮胎模型的最大等效应力为47.4 MPa,增大了0.7 MPa,最大值均在越障时出现,而且都在胎圈内侧部位,与实际情况相符合。
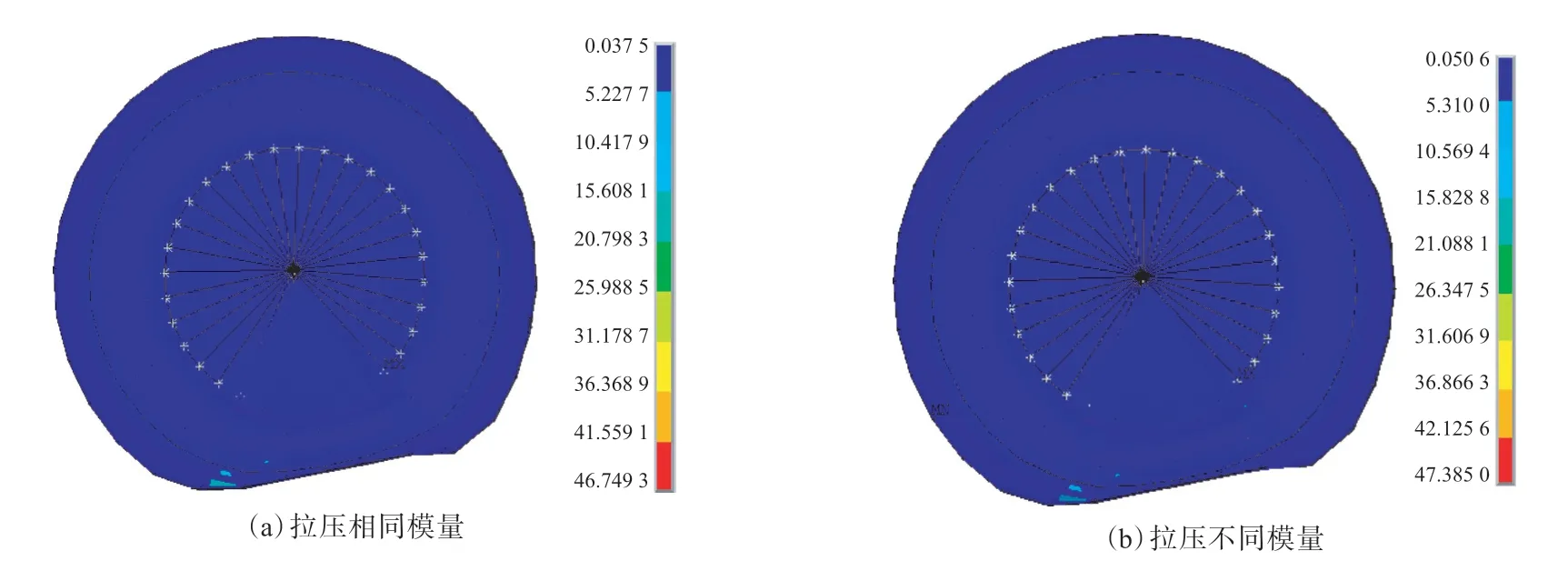
图11 轮胎等效应力分布
轮胎增强帘线正应力分布如图12所示。
从图12可以看出,在滚动工况下,经典各向同性弹性理论轮胎模型增强帘线的最小正应力约为2.7 MPa,拉压不同模量弹性理论轮胎模型增强帘线的最小正应力约为2.3 MPa,两者均大于零,即轮胎充气过程导致增强帘线始终处于拉伸应力状态。
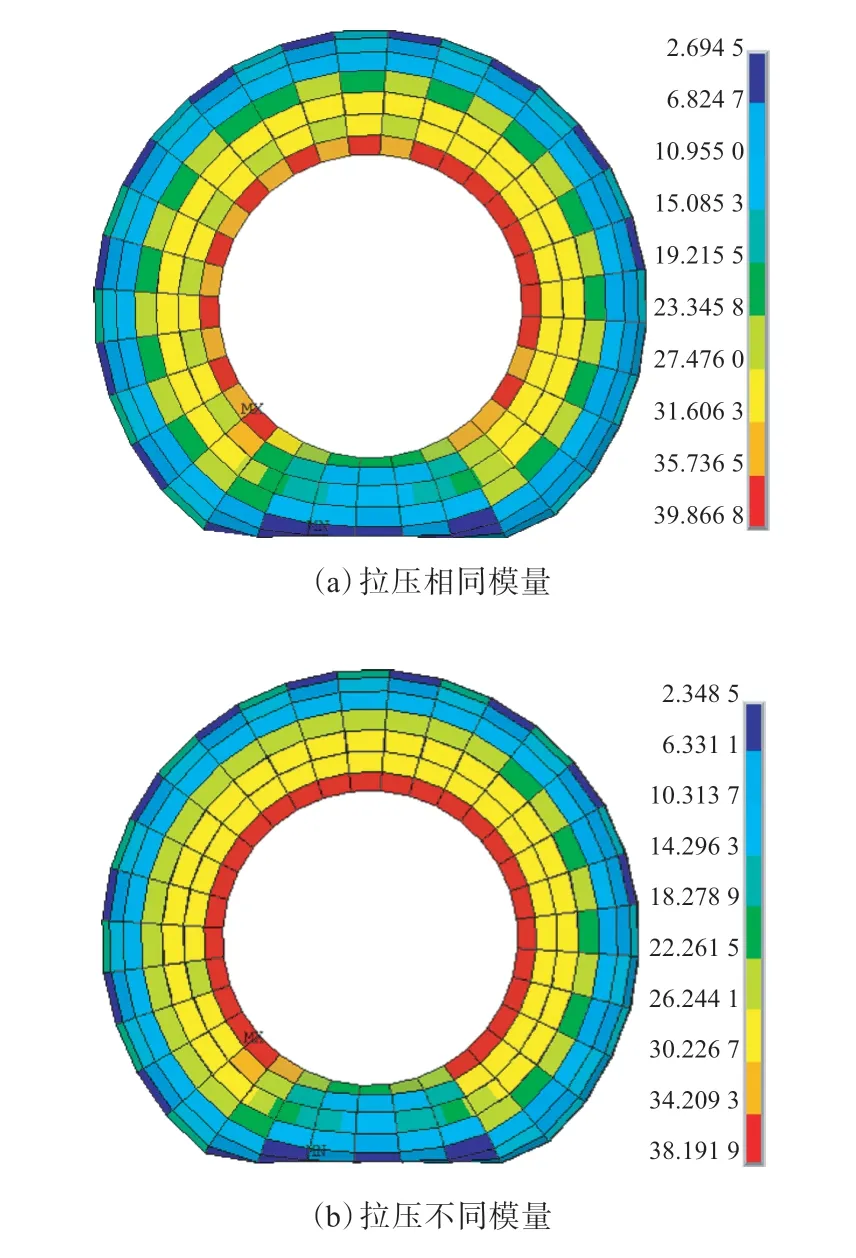
图12 轮胎增强帘线正应力分布(充气压力0.248 MPa)
胎内气体体积时间历程响应分析结果如图13所示。
从图13可以看出,胎内气体体积的变化趋势在滚动状态时出现差异,这是由于轮胎在越障时与路面接触负荷变化引起复杂的应力、应变,轮胎同时承受拉伸和压缩变形,帘线材料的拉压弹性模量不同,表现出来的拉压力学特性也不同,使胎体在滚动时的变形与将帘线材料视为各向同性材料的经典各向同性弹性理论模型有一定差异。

图13 胎内气体体积时间历程响应分析结果
为更好地展现轮胎在复杂路况下各部位受力状态,将模型负荷步2的充气压力改为0.220 MPa,其他工况保持不变,对两种轮胎模型增强帘线的正应力进行对比分析,结果如图14所示。
从图14可以看出,经典各向同性弹性理论轮胎模型增强帘线的最大正应力约为37.8 MPa;拉压不同模量弹性理论轮胎模型增强帘线的最大正应力约为38.7 MPa,增大了0.9 MPa,并出现了压应力,约为1.8 MPa,说明轮胎在滚动时既有拉应力,也有压应力。两种模型最大应力均出现在胎圈内侧边缘,这是由于胎圈与轮辋过盈配合,配合部位的应力较大。仿真结果与实际使用情况较为吻合,轮胎在使用过程中胎圈内侧边缘相对容易磨损。

图14 轮胎增强帘线正应力分布(充气压力0.220 MPa)
4 结论
结合拉压不同模量弹性理论,通过编写UPFs用户子程序对ANSYS软件进行二次开发,将子午线轮胎帘线材料的拉伸弹性模量与压缩弹性模量按10∶1进行参数设置,建立更符合轮胎实际结构特征的三维数值模型,模拟子午线轮胎充气与越障滚动工况,并通过与经典各向同性弹性理论模型分析结果进行对比,研究材料的拉压不同弹性模量力学特性对轮胎受力情况的影响。结果表明:在静态加载工况下,胎内气压使轮胎受预拉应力作用,没有压应力存在,因此经典各向同性弹性理论轮胎模型与拉压不同模量弹性理论轮胎模型的计算结果是相同的,可以不考虑材料的拉压不同弹性模量的性质;在滚动越障工况下,两种模型的应力分布有一定的差异,拉压不同模量弹性理论轮胎模型的最大等效应力增大0.7 MPa,且出现了压应力,能更真实地反映轮胎在滚动时的实际受力状况。
本工作的分析方法和研究结果可为轮胎结构设计与优化提供一定的参考。

