粗糙地面上复杂目标的电磁散射特性
付 松,黄秀琼,周龙建,何思远,陈茹萌
(1.中国西南电子研究所,成都 610036;2.武汉大学电子信息学院,武汉 430072)
粗糙地面与复杂目标的耦合电磁散射的研究一直是雷达目标识别领域比较有价值的研究课题[1],在军事领域,实际地海环境中目标的散射是实现目标识别并精准打击的重要依据,在民用领域,要实现对地面植被、农作物实时监测的前提就是能获取目标在环境中的散射情况。实际情况中,目标总是存在于一定的环境中的,如海上的舰船、地上的坦克、运输车,低空飞行的飞机等,它们都与其所处的环境形成了复合目标模型,因此进行目标识别的关键就是如何从目标和环境的复合模型中提取目标的有效信息[2-5]。在过去的研究中,人们把环境和目标的散射分为两个分支领域来讨论,环境为面散射,而目标则被认为是体散射。通常,在单独研究复杂目标或者是粗糙面的电磁散射问题时,会对另一个问题进行简化从而降低复杂性。但对于要求全方位、实时、高精度的电磁散射领域的发展趋势而言,让这些考虑显得愈来愈不合理。对于实际的工程问题,例如雷达目标检测以及对复杂环境中存在的目标(如地面上的坦克、装甲车或者海面上的舰船等)进行目标识别时,需要客观地考虑复杂环境散射对目标的电磁散射的影响,在进行研究时,不仅要对目标和环境各自独立的电磁散射进行研究分析,而且还需要对它们之间存在的电磁耦合作用进行充分的研究。因此,对环境中复杂目标的电磁散射特性进行快速又准确的仿真计算可以为抑制杂波干扰、提高制导水平以及武器仿真等军事方面以及环境监测、农业技术、煤层勘探等民用方面提供了强有力的支持[6]。
在国外,由Johnson带领的团队[7]对导体目标与垫面之间的耦合散射进行了研究,采用的是“四路径”模型,因为具有简单的表达形式,一直被广大研究者所借鉴;Pino等[8]也对海面与简单舰船目标的复合电磁散射问题进行了研究,采用的方法是前后向迭代与谱密度加速法。同时,中国主要针对粗糙海面与复杂目标的散射也进行了大量的研究实验。复旦大学金亚秋教授团队[9]利用解析方法、数值方法以及两者的混合方法对粗糙海面与二维舰船目标的散射进行了研究。中国电波传播研究所的康士峰团队则利用矩量法(method of moments, MOM)对二维目标和二维粗糙面复合的后向散射幅值和相位分布特征进行了研究。武汉大学朱国强等[10]也对粗糙面上复杂目标的电磁散射进行了研究工作,只有从电磁散射机理出发来对复合目标的散射特征来进行研究分析才能从根本上解决图像解译的问题。张羽绒等[11]提出了一种粗糙地面上复杂目标散射中心参数化建模的方法,首先从几何模型出发,采用空间射线追踪提取目标的散射源,使用正向推算的方法确定参数,从而建立目标的参数化模型。
现将散射中心参数化建模方法中的单独复杂目标扩展到地环境中的目标,并在参数化建模过程中,增加了复合模型中劈结构的参数化模型,基于劈边结构的识别算法,增量长度绕射系数理论以及属性散射中心模型,对直角外劈的散射中心参数化模型进行了构建和验证,使得最终建立的粗糙地面上复杂目标的参数化模型更准确,从而有利于雷达目标识别。
1 粗糙地面的数值仿真方法
若要对粗糙地面上复杂目标电磁散射特性进行仿真,首先便是需要建立粗糙地面与复杂目标的一体化几何模型。对于粗糙表面的模拟通常具有明确的数学解析表达形式,定义一个z=0的虚拟基准面,并用z=f(x)来描述粗糙面的高度起伏特性,这个函数与粗糙面的统计参量均方根高度h以及相关长度l相关。采用蒙特卡罗(Monte Carlo)方法来模拟生成随机粗糙表面[12],这种方法的基本思想是利用功率谱函数对频域的每个分量进行滤波,其关系可以表达为
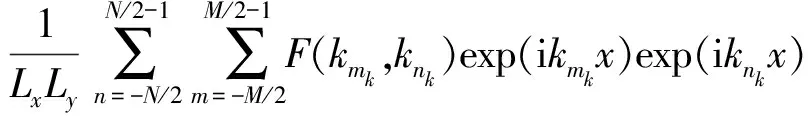
(1)
(2)
式中:Lx、Ly分别为粗糙面下x、y方向的截断尺寸;kmk、knk为波数;W(kmk,knk)为粗糙面的功率谱密度;N(0,1)为具有0平均值、标准偏差为1的正态分布随机数;M、N为离散数量;Δx、Δy为离散间隔。
为了让f(xm,yn)为实数,必须满足:
(3)
通过对比高斯谱粗糙面和指数谱粗糙面所进行的数值建模结果,指数谱粗糙面更符合实际地面的粗糙情况,其功率谱密度函数为
(4)
2 粗糙地面上复杂目标的散射中心参数化建模研究
2.1 粗糙地面上复杂目标基于面元的散射中心分离技术
基于空间射线分集技术和射线追踪技术对粗糙地面上复杂目标的散射中心进行提取,具体的实现步骤如下。
步骤一在给定的入射角度和观察角度下,对已经建立的粗糙面与复杂目标的复合几何模型表面进行射线追踪,确定射线在复合目标表面的传播路径,并根据路径对射线进行归类和分集。
步骤二利用几何光学中的反射、散射现象描述空间中射线的传播情况,并利用物理光学计算每条射线携带的能量,用混合几何光学-物理光学(geometric optics-physical optics,GO-PO)方法计算耦合作用的射线的能量,通过将同一路径的射线能量相叠加即得到射线子集的散射贡献。
步骤三上述步骤二中的射线子集即为潜在的散射中心,最后将其按贡献大小排序,筛选出贡献强、占主导作用的子集作为散射中心,这里根据计算设定目标总的散射贡献值作为门限阈值。
首先假设目标几何模型被分解为M个实体部件,并用I1,I2,…,IM来标记每个部件,入射平面波也被模拟为一个射线总集U={ri,i=1,2,…,N},其中ri∈U代表其中的某一条射线,N是射线的总条数。然后利用射线集照射到目标表面来实现射线追踪,例如一条射线ri入射到一个三角面元ti上,三角面元的中心为Qi,则该三角面元的索引号被记录为IQi,然后将该射线的反射射线作为入射波继续在目标表面进行追踪,并按顺序记录下与该条射线发生作用的三角面元,直到射线离开目标表面为止。若根据射线追踪顺序记下的与射线ri发生作用的三角面元中心为[Q1,Q2,…,QN],那么就可以用[IQ1,IQ2,…,IQN]来标记射线ri的路径。
要求得复合目标的总散射场,在确定了射线在复合目标表面的传输路径并采用传输矩阵来描述后,还需要对每一条射线上的贡献单独进行计算,然后将所有射线的贡献叠加得到每个等效散射中心的贡献。对于只作用于一个面元的射线直接采用PO法计算射线上的散射能量,而对于作用于两个或两个以上面元的射线而言,采用混合GO-PO方法来计算面元上的散射能量,即采用几何光学来确定射线的路径,计算射线的反射场,然后在最后作用的面元采用PO法来计算散射场总场。
假设经过射线追踪后,得到射线ri和目标表面的作用点依次为Q1,Q2,…,QN,则沿该射线路径上的场幅值可以通过式(5)确定:
(5)
式(5)中:Einc为入射波,且Einc=E0e-jkir;SGO(Qn)为通过GO法计算的反射点在Qn上的反射矩阵;SPO(Qn)为用PO法计算最后一个反射点Qn上的散射矩阵。

(6)
式(6)中:An为GO幅值的扩散系数,当入射波是平面波时,An=1;tn为点Qn和Qn+1之间的距离;R(Qn)为点Qn处的反射矩阵。
(7)
SGO(Qn)=R(Qn)exp(-jktn)
(8)
用PO法计算复合目标表面的散射场为

(9)

(10)
式(10)中:IA为相位积分项,即

(11)
通过上述步骤,将入射波模拟成一簇射线集照射到目标表面,通过空间射线分级技术将射线分类为很多个射线子集,其中每一个子集都是潜在的散射中心。筛选强散射源的具体步骤为:首先在给定入射条件下,计算目标的总的RCS作为阈值;然后在该入射条件下,计算每一个散射源的RCS,并将其从大到小排序,将小于-20 dB的散射源舍去,留下的散射源作为候选;最后对排好序的候选散射源的RCS从大到小叠加并将其与目标总的RCS做对比,若两者的均方根误差小于2 dB,则认为这些散射源就可以描述目标的散射特性了,否则就还需要从候选的散射源中继续增加散射中心的数量,直到这些散射中心叠加的RCS与目标总的RCS的均方根误差小于2 dB,最后将这些散射中心的信息输出。
2.2 属性散射中心参数化模型
基于属性散射中心模型的形式能够正向确定模型中的参数,建模流程为:先从复杂目标复合的CAD模型出发,将目标表面分解为多个实体部件及其二级表面分区组合[13-14];再基于已分解的CAD模型,采用空间射线分集方法将作用在目标表面的空间射线归集为部件级射线子集合与二级表面级射线子集合。然后采用基于PO与GO的高频算法计算分离出的散射源的散射场,并依据散射场的大小将部件级散射源进行排序,筛选出强散射源作为散射中心;属性散射中心模型的表达形式为

exp(-kcγisinφ)exp[-j2k(xicosφ+yisinφ)]
(12)
式(12)中:A为散射中心的幅度参数;L为散射中心的长度参数;α为频率依赖参数;φ为入射波方位角,取值范围为[-φm/2,φm/2],其中φm为最大成像观测角;φ′为描述分布型散射中心成像方位角的偏离程度的参数;ri=(xi,yi)为第i个散射中心的二维位置,是三维位置矢量在成像面上的投影。
复合模型的总散射场由复杂目标自身的l个独立散射中心贡献、粗糙地面的p个独立散射中心贡献以及地面与复杂目标耦合形成的q个独立散射中心贡献之和,即:
(13)
Si=[Ai,αi,(xi,yi,zi),Li,φi,γi],
i=1,2,…,l+p+q)
(14)
因此只要完成复杂目标散射中心物理相关参数正向推算,输出强散射源的同时输出散射中心的幅度参数、三维位置参数、长度参数与频率依赖参数后,粗糙地面上复杂目标的散射中心参数化模型既可建立。
2.3 散射中心模型中参数的正向确定方法
2.3.1 位置参数的确定
由式(12)可以看出,位置参数是影响散射场相位的主要因素,因此只有明确了散射中心的位置参数,才能对散射中心的频率和长度等参数进行更有意义的分析。位置参数(xi,yi)是三维的散射中心(xi,yi,zi)位置的投影,也即是SAR图像中“亮点”的位置,其中xi为距离向坐标、yi为方位向坐标,与(xi,yi,zi)的对应关系如下:
rproj=Proj(r;θ,φ)=T(θ,φ)r
(15)

(16)
接下来对三维位置信息进行分析,三维位置即面元的作用点的三维信息,主要包括以下两种情况:一是当射线仅与复合目标表面发生一次作用,则直接将作用面元的中心点Qn(xn,yn,zn)记为反射点。二是若射线与目标表面发生了多次耦合作用,则需要对作用点进行等效作为等效反射点。
基于以上两种情况,在已知等效反射点后对散射中心贡献的来源进行分析。
(1)若只有一条射线构成散射中心的射线子集,则该射线等效反射点的位置就是散射中心的位置。
(2)若有多条射线构成散射中心的射线子集中,为求得该散射中心的位置,则需要使用加权平均法来分析该子集中的每个射线的等效反射点坐标。其中加权平均法规定射线反射作用点加权的值为该射线在面元表面上激发的感应电流的强度,则该散射中心的三维坐标为
(17)
式(17)中:wn=|Js(Qn)|为目标表面的感应电流强度;Qn(xn,yn,zn)为该射线的等效反射点。因此,对于与目标表面进行多次作用的射线,在得到等效反射点后,对射线经过目标表面的最后一个面元求加权值即可。
2.3.2 长度参数的确定
长度参数L主要描述散射中心的幅度响应与方位角的依赖关系,它是散射中心在SAR图像方位向上的有效展布长度。散射中心根据幅度对方位的依赖不同分为分布型和局部型散射中心两类。局部型散射中心在SAR图像上表现为一个“亮点”,因此长度参数为0;而对于平板、二面角等散射结构在特定姿态下形成的分布型散射中心,它们在SAR图像上呈现为一条“亮线”,“亮线”的分布长度即长度参数。因此只要在分布型散射中心的射线集合中找到“亮线”的两个等效端点,那么通过对两端点进行投影并相减就能得到该散射中心的长度参数,即
L=|(xm-xn)sinθsinφ-(ym-yn)sinθcosφ|
(18)
式(18)中:(xm,ym)和(xn,yn)分别为两个端点在x轴和y轴的坐标位置;θ、φ分别为入射波的俯仰角和方位角。
2.3.3 频率依赖参数的确定
频率依赖参数α描述了散射中心的散射强度与频率的相关程度,通过读取目标的几何信息并判断每个散射中心包含的散射机理来确定频率依赖参数α,表1中给出了一些典型几何体对应的α值。

表1 几种常见几何结构的α参数取值
3 基于劈边结构的散射中心参数化建模
在某些特定角度下,劈边缘结构的绕射贡献远远大于面类结构的绕射贡献[15],因此想要获得更加准确的参数化模型,需要在这些角度下对粗糙地面上复杂目标中的劈边结构进行参数化建模。
3.1 劈边结构识别算法
为了计算劈边的绕射贡献,首先要对劈边结构进行识别和提取。几何模型的剖分会使得相邻的小三角面元之间会构成棱边的结构,一定程度上便利了劈边的识别,但也产生了许多影响结果的虚假边缘,比如:对于目标的同一表面上,相邻的三角面元之间虽然构成了棱边,但其并不真实存在,且并未产生绕射贡献,因此不可以被归类为边缘。

图1 边缘结构几何示意图


图2 外劈、内劈的几何示意图
通过上述步骤筛选出符合规则的真实劈结构,并且获取该劈边的起点、终点坐标,以及构成该劈边的两个面元的单位法向向量;然后对劈边结构进行合并,对得到的劈边一一标号,并将所有边的单位向量取为沿坐标轴增长的方向;最后采用遍历的方法,找寻单位向量完全相同、且有公共点的棱边,由平行且共点同属于一条线段,且劈边方向均为沿坐标轴增长的方向,可首尾相连的原则,将其劈边合并成目标表面的边缘。
3.2 增量长度绕射系数理论(ILDC)计算劈边结构的绕射场
一个简单的劈结构在入射平面波照射下,该结构边缘绕射的角度关系如图3所示。
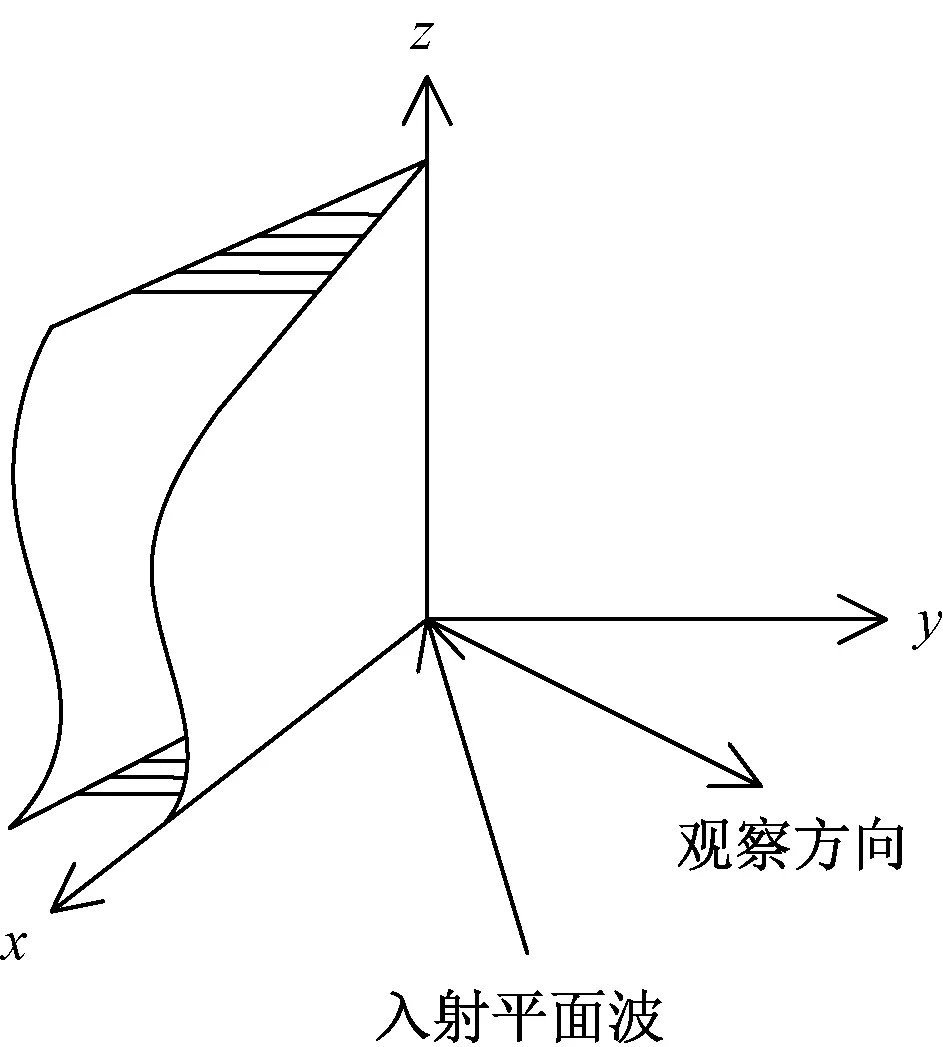
图3 劈结构在平面波入射下的示意图
增量长度绕射系数理论(the theory of incremental length diffraction coefficients,ILDC)的绕射系数为d////、d⊥⊥、d//⊥由等效电磁流法(the method of equivalent currents,MEC)的绕射系数、物理光学两项组成[16],可以表示为
(19)
(20)
(21)

(22)

(23)

(24)

(25)

(26)

(27)
式中:
(28)
sinα1=[sin2βi-sin2βscos2φs]1/2/sinβi
(29)
sinα2=[sin2βi-sin2βscos2(nπ-φs)]1/2/sinβi
(30)
(31)
(32)
综上,利用ILDC计算的远区绕射场可以表示为
(33)

基于上述方法对劈边结构进行识别及分离,获取了劈边三维位置、方向向量信息以及劈面的三维位置、外法向向量信息,以及基于ILDC计算了劈边缘的绕射场后,同样基于属性散射中心模型进行劈边缘的正向参数化建模,下面以一个直角外劈为例,对劈结构的参数化模型进行分析。
3.3 直角外劈的散射中心参数化模型
构建一个PEC直角外劈,由两个20 m×10 m的无厚度长方形平板构成,劈边长度为10 m,如图4所示,对该劈进行分解,可以得到两个劈面以及一条劈边共3个区域。

图4 劈边长10 m的直角外劈模型
给定姿态角为θ=90°,φ=-45°,选定入射波频率为f=9.6 GHz,在当前入射角度下,劈面1、2的法向向量与入射波均偏离了135°,对于单站来说,此时两个劈面的后向散射方向已经偏离入射波镜面方向太大,使得此时面元的散射回波几乎仅有很微弱的一部分回到接收处,因此两个劈面不是强散射中心。而该角度对于劈边来说,恰好是正入射,因此劈边贡献最强,劈边成为强散射源,因此需要对劈边缘进行参数化建模,表2给出了φ极化边缘的参数信息。

表2 边缘参数
在该角度下建立边缘的参数化模型,图5(a)给出了在-45.895 3°~-44.104 7°的小角度变化范围内重构的SAR图像,采用分辨率为0.5 m×0.5 m,频率范围为f=9.45~9.75 GHz,步进为Δf=0.002 5 GHz,角度步进为Δφ=0.014 9°;图5(b)给出了相同参数下基于PO的高频预估仿真计算的SAR图像。

图5 直角外劈的重构SAR图像与高频预估仿真SAR图像
从图5可以看出,参数化重构与高频预估的SAR图像位置及亮度均非常吻合。在该角度下,由于面类结构的散射贡献非常弱,仅有的一条边缘成为主要贡献来源,且其是点散射中心,因此仅有一个亮点。
4 算例分析
基于上述算法,对粗糙地面上复杂目标的参数化模型进行了构建,并重构了复合模型的SAR图像,与MSTAR库中最接近角度下的SAR图像进行对比,验证了算法的有效性。
粗糙地面以尺寸Lx=Ly=640λ,相关长度lx=ly=128λ,均方根高度h=1.28λ,剖分网格单元长度3.2λ的指数粗糙面为例,坦克T72根据查询到的资料采用ANSYS进行自底向上的几何建模,并对复合模型进行实体部件分解处理,复合模型的部件分解示意图如图6所示。其中部件1(无法照亮的坦克底部)以及8旁边的小部件9没有标出。

图6 地面与坦克T72复合模型的实体部件分解示意图
在入射角θ=73°,φ=60°,入射频率f=9.6 GHz下对粗糙地面上的坦克目标T72进行强散射中心提取,结果如表3所示。然后基于重构SAR图像,与MSTAR库数据(子类名称为SN_132)最邻近方位角的SAR图像进行对比计算相似度。
从表3中和SAR图像中可以看到37个散射中心,其中由坦克独立散射形成的散射中心为25个,由地面独立散射形成的散射中心为0个,由于两者耦合形成的散射中心有12个,并且所有的散射中心均为局部型。然后从散射机理出发来对每个散射中心进行分析,表3中序号为1的散射中心,也是SAR图像中幅值最强的散射中心,是由部件24(坦克炮塔表面)与46(地面)耦合作用形成的,散射中心2是坦克部件29(左轮盖)与24(坦克炮塔表面)二次作用形成的,散射中心3是24(坦克炮塔表面)的曲面反射形成的散射中心,其他散射中心也可以参照类似的方法分析,每个散射中心都有相对应的散射机理,这便是散射中心参数化模型的特点之一。再对参数化建模重构的SAR图像和实测的SAR图像进行分析,从图7都能看出坦克T72目标的轮廓特征,且重构SAR图像与实测SAR图像的图像相似度为69%,证明了参数化建模与实测结果具有较好的一致性。但是总的来说实测的散射中心个数比参数化模型重构和仿真的散射中心个数都要多。据分析,这是由多方面原因造成的,一方面是实测的地面与仿真的地面具有一定的差异,没有办法获取具体的实测地面信息,另一方面是实测图像进行了一些限幅处理,让贡献较小的散射中心也在图像中显现出来。

表3 粗糙地面上的坦克T72目标在θ=73°,φ=60°, f=9.6 GHz下的散射中心特性提取结果

姿态角为θ=73°,φ=60°,分辨率为0.25 m×0.25 m
5 结论
主要对粗糙地面上复杂目标的散射中心参数化模型进行了构建,包括复合目标中的面类结构和劈边结构的散射中心参数化模型的构建。具体的实现步骤为:首先,对粗糙地面进行数值仿真,对复杂目标进行几何建模,并对复合模型进行部件分解;其次,利用空间射线分集技术和射线追踪技术分离出复合目标的散射中心,基于属性散射中心模型的形式,确定散射中心的相关参数;最后,建立粗糙地面上复杂目标的参数化模型,将重构的RCS特性和SAR图像特性与实测结果进行对此,验证了本文方法的有效性。并对劈边结构的散射中心参数化建模方法进行了初探,基于劈边结构的识别算法,增量长度绕射系数理论以及属性散射中心模型,对直角外劈的散射中心参数化模型进行了构建,并与基于GO-PO方法的高频预估结果进行对比分析,验证了本文方法的有效性。
因为环境的复杂性,研究工作还存在很多不足。在研究过程中没有考虑粗糙地面和目标的介电特性,希望以后工作中能有所改进。然后只对直角劈结构进行了参数化建模,但由于复合目标存在着较多的弯曲边缘,因此对复合模型进行建模时没有考虑劈边绕射,因此以后的工作还需要针对弯曲边缘的提取、合并与分离进行进一步的研究,以此提高边缘结构仿真的精度。

