多旋翼飞行器建模与控制器设计

杜 明，赵燕飞，范书瑞，贾颖淼，吴佳飞

(1.中国电子科技集团公司第五十四研究所，石家庄 050081；2.天津市海河管理中心，天津 300231；3.河北工业大学电子信息工程学院，天津 300401)

多旋翼飞行器又称无人机，其构造简单紧凑、行动十分灵巧、运动格外稳定[1]，在军事领域与民用领域均展露出很大的应用价值，四旋翼机已广泛应用于航空摄影、遥感测量、实时监测、军事侦察、农药喷洒等行业[2-4]。但是其同样拥有续航时间短、载重量低等问题，在配送东西过程中难免会遇到悬挂的东西掉落的问题，造成无人机的不平衡，如何让无人机在悬挂质量突然增加或者减少的情况下能够快速恢复平衡是一大难点。

如今，随着无人机的研究逐渐深入，中外的诸多科研机构和大学都对四旋翼无人机进行了很深入的研究。目前相关专家提出了很多四旋翼无人机的控制方法，其中最经典的就是比例积分微分(proportion integration differentiation，PID)控制[5]。PID控制有着原理简单、控制技术成熟、易于实现的优点。Ji等[6]提出了倾斜四旋翼机的新概念，独立控制无人机的旋转与平移，建立了一个完整的动力学模型，其中考虑了参数不确定性和外部干扰，提出了一种自适应快速有限时间控制方法，最后通过对比仿真实验验证了控制器的有效性和鲁棒性。Zhang等[7]提出了一种预测滑膜控制方法，并将其应用于飞行器的运动控制中。实现了在干扰环境下的跨域过渡，最后通过与PID控制器的对比仿真，验证了控制方案的可行性与鲁棒性。Cervantes-Rojas等[8]开发了一种自适应控制器来解决四旋翼机的轨迹跟踪问题，提出了利用神经网络与模糊推理系统进行交互作用的模式。在室外环境进行实验，证明了基于动态域名服务(dynamic domain name server，DNNs)和高木-关野(Takagi-Sugeno，T-S)技术相结合的算法相对于经典的控制器具有更好的性能。南京航空航天大学从1958年开始才进行无人机方面的研究。王源等[9]提出直接坐标法控制无人机的飞行轨迹，实现四旋翼无人机自主导航控制，有效地保证系统稳定性和响应的快速性。2015年北京航空航天大学提出了一套基于自抗扰控制的姿态解算法[10]，该算法很好地解决了无人机系统状态耦合性高和建模产生的状态误差问题，所设计的自抗扰控制系统在快速响应、无超调的前提下，具有很强的抗干扰能力以及较高的控制效率。2018年，王春阳等[11]提出了一种基于线性自抗扰的轨迹跟踪控制系统设计方案，可以很好地克服无人机的强耦合性、模型不确定性以及外部干扰问题，满足无人机姿态调节快速和高稳定度的控制要求。

在充分了解无人机的结果和飞行原理的前提下，现利用最简单也最经典的PID控制，调整PID参数，使无人机在悬挂质量突然改变的情况下快速恢复平衡，持续稳定飞行，在Simulink上搭建系统模型，得到仿真结果，证明飞行器可以得到稳定有效的控制，提高飞行器的性能。

1 数学模型建立

1.1 坐标系的转换

四旋翼无人机在空间飞行时，为了方便地描述无人机的转动方程，建立了四旋翼飞行器的机体坐标系，它的坐标原点是飞行器的中心，xy水平面即是4个旋翼所在的水平面，z轴垂直于xy水平面。此种坐标系建立在飞行器本身上最为方便,可以用B表示。地面坐标系是建立在假设地面为水平面的基础上，一般用E表示。

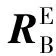
(1)

(2)

(3)

(4)

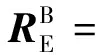
(5)

式中：θ、ψ、φ为欧拉角，用来描述E系到B系转换需要的角度；θ为俯仰角，表示无人机与水平面之间形成的夹角；ψ为偏航角，表示无人机在地面的投影和地轴之间的夹角；φ为滚转角，表示无人机绕中心对称轴旋转过的角度。

1.2 动力学数学模型

无人机的数学模型可以分为线性运动的数学模型和角运动的数学模型，线性运动的数学模型可以根据经典力学的理论来描述。由于无人机各项参数十分复杂，在最后对控制效果影响较小的前提下，做以下假设。

(1)将四旋翼飞行器视为刚体，在飞行器的聚合中心有着均匀的纹理和质量中心分布。

(2)忽略飞行器的四个旋翼与其相应电机之间的摩擦以及四旋翼飞行器中的空气摩擦。

(3)由于四旋翼飞行器的飞行高度不是很高，因此受到地球重力的影响也非常小，所以认为它受到的重力在飞行过程中受到的重力不变，即重力加速度不会改变。

(4)假设由旋翼旋转而产生的升力垂直于相应的旋翼，则该升力的大小与旋翼的转速的平方呈线性关系。

四旋翼飞行器飞行过程中飞行过程中主要受到3个力的影响，这3个力是旋翼产生的拉力，飞行过程中的阻力和来自地面的重力[12]。可得四旋翼飞行器在地面坐标系中的受力表达式[式(6)]，四旋翼飞行器的线性运动数学模型表达式[式(7)]。

(6)

(7)

(8)

(9)

(10)

式中：L为电机轴中心到无人机质心之间的距离；Jr为旋翼的转动变量；c为空气阻力系数；p、r、q为机体沿三轴方向的角速度分量；d为反扭矩系数，且Ω=Ω1+Ω2-Ω3-Ω4。

因为四旋翼飞行器的结构对称，所以机体整体转动惯量可以用式(10)表示，即

(11)

式(11)中：I为刚体对定轴的转动变量；Ixx、Iyy、Izz为3个方向上的转动惯量。

将式(10)与式(11)综合便可以得到四旋翼飞行器在机体坐标系中的角运动表达式，如式(12)所示。

(12)

2 PID控制方法

2.1 PID结构

姿态控制算法主要是采用串级PID控制[13]，这种控制系统不仅原理简单、鲁棒性强，而且通用性高。四旋翼飞行器运动过程中需要控制的量包括3个位置量：x、y、z和3个姿态控制量：θ、φ、ψ。单个闭环PID控制器[14]很容易减慢系统处理速度。由于姿态角的变化与位置坐标的变化之间存在因果关系，因此控制系统采用顺序控制进行双重设计闭环PID控制。内环是用于调整无人机姿态角变化的姿态控制环，外环是用于控制无人机位置坐标变化的位置控制环。这种串级控制方法往往都会取得不错的效果。

PID的结构图如图1所示，PID的输入信号为e(t)，输出信号为u(t)。它主要可以分为比例、微分和积分三部分，比例是PID控制器的基础部分，一切都是围绕比例部分作用的。积分部分是为了消除因比例部分带来的稳态误差，而微分部分则是抑制积分带来的超调作用。这三部分的不同组合将会带来不同的作用，因此调整3个控制系数对于PID控制来说十分重要。

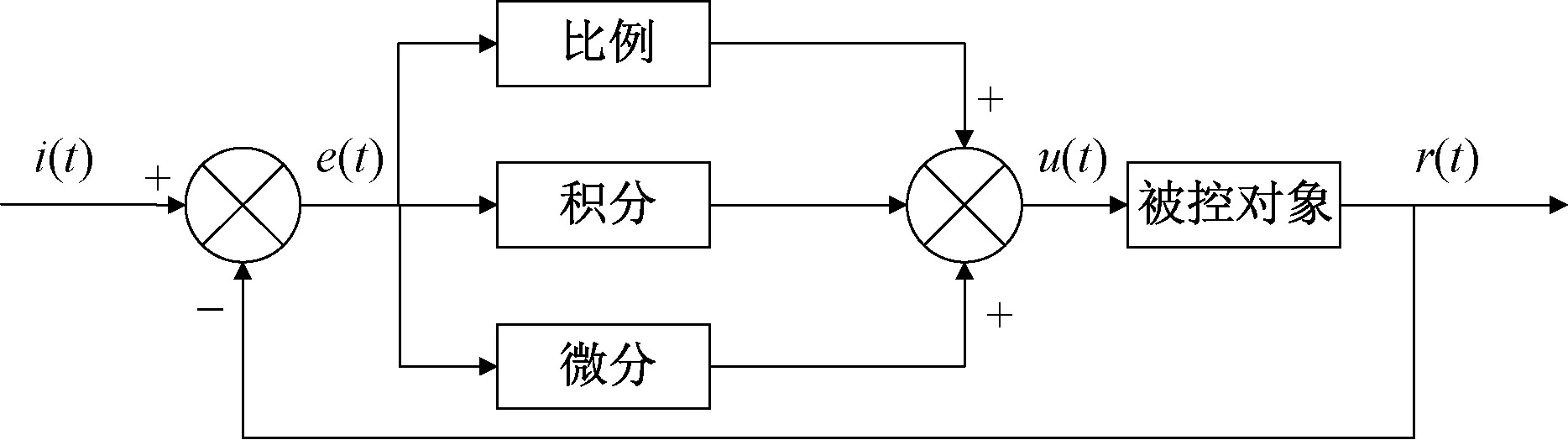
图1 PID结构

e(t)=i(t)-r(t)

(13)

(14)

式中：i(t)为PID输入的信号；r(t)为系统实际输出的信号；Kp为比例系数；Ti为积分时间常数；Td为微分时间常数。

参数整定是PID控制器的核心，也是其最难的部分，直接在控制系统中通过不断的试验去调整参数，这种方式简单不需要很复杂的数学计算，并且调试成功后更加贴近实际应用，但缺点就是太过耗费时间并且对试验人员的经验要求很高。实验调整PID的参数步骤如下。

(1)合理确定一个采样周期，确保系统能够稳定运行。

(2)调整系数的大小直到系统将要出现振荡现象，与此同时，仔细观察记录比例系数和临界振荡周期。

(3)利用数学公式解算出PID控制器参数。

2.2 数字模型的简化

为了方便四旋翼飞行器的控制器设计，需要考虑到实际情况增加约束条件，进而使数学模型在合理的范围内得到最大程度的简化。当小型四旋翼飞行器在室内慢速飞行时，由于没有风力的干扰，且转动速度十分缓慢，所以能够添加以下约束条件。

(1)忽略空气阻力因素带来的干扰，即把空气阻力矩和空气阻力的大小看作0。

(2)因为实验用的是小型四旋翼飞行器，其4个螺旋桨无论是质量还是尺寸都十分小，因此忽略陀螺效应力矩，即Jr为0。

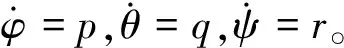
为了方便描述，令

(15)

当在无风条件下或者是只对无人机产生小角度干扰的环境下，低速稳定飞行或到达悬停状态时进行无人机实验，由于无人机的飞行姿态角度变化很小，所以空气阻力因素和陀螺效应都可以暂时忽略，故可以在上面的基础上进一步简化无人机的数学模型，从而达到如式(16)、式(17)所示的最简模型。

(16)

(17)

2.2 外环位置控制算法

位置控制环可通过PID计算获得运动方向上的3个预期加速度，例如预期位移与实际位移之间的差，各方向的计算公式为

(18)

式(18)中：kPi、kIi、kDi(i=x,y,z)分别为比例系数、积分系数和微分系数；xd、yd、zd为3个方向上的预期位移；x、y、z为实际位移。

图2 位置控制流程图

由式(19)可得U1，再输入期望偏航角得出期望的滚转角和期望的俯仰角为

U1=

(19)

(20)

式(20)中：下角标e表示该物理量的期望值。

2.4 内环姿态控制算法

在内环姿态控制也是串级结构，首先将外环送来的期望姿态和实际反馈回来的值输入给角度控制器，角速度控制器根据期望角速度与实际角速度算出U2、U3和U4的值，最后将其变换为电机的期望拉力解算出各旋翼的期望转速公式为

(22)

式中：kPi、kIi、kDi(i=2,3,4)分别为比例系数、积分系数和微分系数。

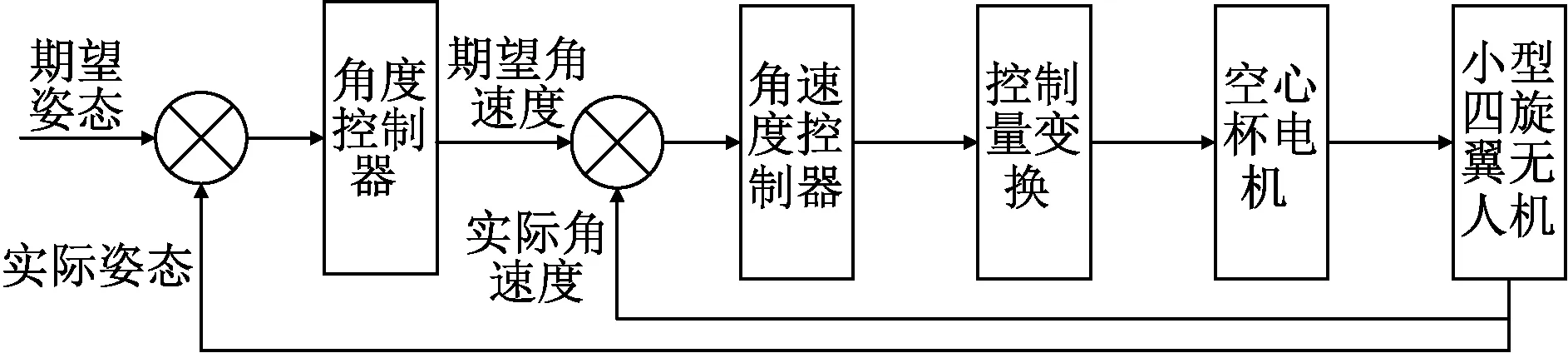
图3 姿态控制流程图

期望角速度的计算公式为

(23)

白煞留下和铁卫连夜清理黑旗会分坛，因为与黑旗会博弈须要充裕的银子作基础，所以萧飞羽临走时吩咐将所有值钱的东西带去安和庄，余下的事情交给樊虎带领的伙计。白煞和铁卫搜索发现天问大师和紫阳道长要找的少林俗家弟子之首的白云飞竟然囚禁在地牢里。

经过多次试验，最终得到这些PID控制系数如表1所示。

表1 PID参数

2.5 Simulink仿真结果分析

利用上述求出来的PID参数进行模型的构建，在Simulink中进行仿真，得到的外环位置仿真结果如图4所示，其中黑色曲线为x轴的期望位置与实际位置，红色曲线为y轴的期望位置与实际位置，绿色曲线是z轴的期望位置与实际位置。

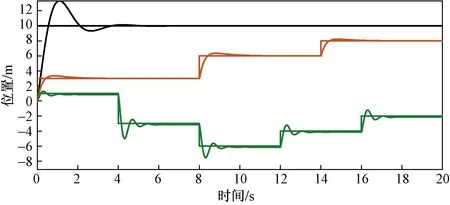
图4 位置仿真结果

仿真模型中预期坐标为x=10，y=3、6、8，z=1、-3、-6、-4、-2，由仿真曲线可知，x点在4 s内实现了无人机从初始坐标到预期坐标的平滑过渡，稳态误差在±4范围内；y点在1 s内实现无人机从原来坐标到预期坐标的平滑过渡，稳态误差在±1范围内，超调量较小，很快进入稳定状态；z点在1.4 s后趋于平稳，高度波动较大，但响应速度快。整体来说，系统可以取得较好的控制效果，使系统迅速稳定下来。

在Simulink中进行仿真得到姿态控制效果，其中俯仰角、滚转角、航偏角的变化分别如图5所示。

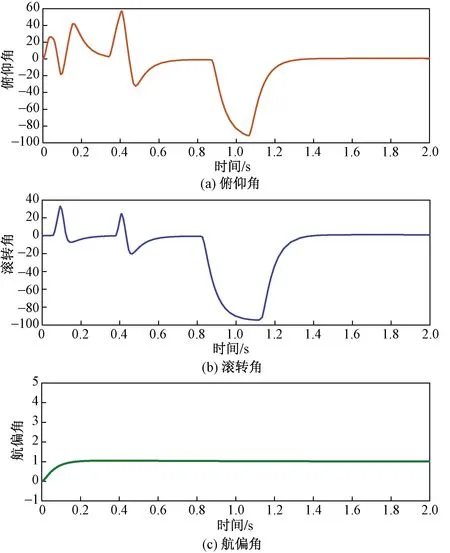
图5 俯仰角、滚转角和航偏角曲线图

图5(a)和图5(b)中，俯仰角和滚转角在曲线波动后基本稳定在期望值零点，其曲线波动较大，最大达到60，最小将近-100，但是控制系统的稳定性较好，基本可以在1.5 s内近似恢复期望值0。图5(c)中，无人机偏航角赋值为1,，使无人机方向不发生变化，无人机在0.2 s内进入固定偏航角状态，能够维持稳定。由此可以看出系统调整速度很快，稳定性良好，取得了较好的控制效果。

3 滑膜控制器的设计

3.1 控制器设计

控制器所要达到的目标是使四旋翼无人机能够在一个固定的高度进行相对悬停，并以指数趋近律为核心来设计滑膜动态控制器[15]。通过公式推导将3个欧拉角θ、ψ、φ解耦，分别对其进行控制以实现整体飞行控制，以下是推导过程

通过反馈线性化，得到的线性系统公式为

(24)

(25)

(26)

(27)

为了方便后续推导，令

(28)

已知s=Cηi，对其求一阶导数，可得

(29)

式(29)中：C为常系数，ε>0,k>0,i=1,2,3；-ks为指数趋近项；-εsgn(s)为等速趋近项。

将式(24)代入式(29)中，得到式(30)，即

ui=(CiBi)-1(-CiAiηi)+s

(30)

式(30)中：Ci=[15 1],Bi=[0bi]T,ε=10，k=3.5，i=1,2,3，ηi=[1 1]T,利用趋近律对四旋翼飞行器的高度z实时控制和反馈。则状态方程为

(31)

式(31)中：f1=[0-g]T，g为重力加速度。

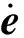
(32)

设切换函数为

(33)

由高度误差变化率可得

(34)

将式(31)和式(33)代入式(29)中，可得式(35)，其中c=30,ε=10,k=3。

(35)

3.2 仿真结果分析

图6是高度z的变化曲线，在图6中可以看到，高度z的曲线在1.5 s内达到稳定，并且没有超调。由此可知设计的滑模控制器可以使四旋翼无人机在一个固定的高度进行相对悬停，图6悬停在5 m处，滑膜控制器可以实现对无人机的控制。

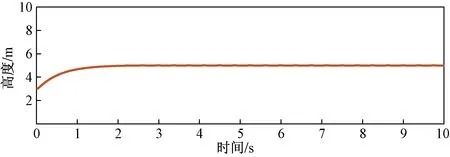
图6 高度z的变化曲线

4 结论

分析了无人机的运动原理，建立了完备的数学模型。在数学模型的基础上做了一个仿真验证，实现了无人机的期望飞行。验证了数学模型的正确性。得到的主要结论如下。

(1)在基本限制条件下进行受力分析，进一步得到了无人机运动的线性运动模型以及角运动模型，最后根据实验条件再进行模型的简化，有利于后期的模型计算。

(2)在Simulink中搭建出仿真模型，经过多次尝试得到的PID控制系统参数可以有效地区控制系统的稳定性，取得较好的控制效果。

(3)设计滑膜控制器，并在Simulink中搭建出相应的仿真模型，可以实现期望的效果，使四旋翼无人机能够在一个固定的高度进行相对悬停。