双行程后坐-准流体延期保险机构

王晓霞，贺 文，文瑞虎，孙诚诚

(机电动态控制重点实验室，陕西 西安 710065)

0 引言

电磁轨道炮作为一种新概念武器，具有电磁发射推力大、弹丸初速高、射程远、无烟雾效应产生等优点。与传统火炮发射原理不同，电磁轨道炮采用兆安级脉冲功率电源放电产生强磁场，载流电枢受到兆牛级安培力推动弹丸，弹丸经历平稳长时高加速过程，最终以超高音速离开轨道炮膛。相对于传统炮弹引信，电磁轨道炮引信将承受更加恶劣的发射环境，如长时高后坐过载、膛内脉冲强磁场、出炮口瞬间的瞬态强电场等[1-3]。这些发射环境信息特征独特明显、容易识别，适合作为引信保险机构设计的环境激励选择。利用长时高后坐过载解除保险是电磁轨道炮引信保险机构设计的常规方案，也是首选方案，但也对保险机构的抗过载能力带来了更大的挑战。

2006年，美国武器研究发展与工程中心(ARDEC)的Barry Schwartz等提出最新研究的24.4 mm口径轨道炮杀伤爆破弹，其引信保险机构为后坐力和磁力的双保险[4]，后坐保险机构为单行程直线惯性机构，结构简单，膛内即解除保险，膛内安全性较差。文献[5]初步设计的电磁轨道炮智能弹药引信保险机构利用后坐力及强磁场作为引信解除保险的两道环境力，隔爆机构选择垂直转子机构；后坐保险机构采用成熟简单的后坐销设计方案，并计算了后坐弹簧的尺寸参数，膛内安全性较差。文献[6]设计的电磁轨道炮电子时间引信采用后坐保险机构和磁保险执行结构作为冗余保险。其中，后坐保险机构采用惯性筒-钢珠-套筒串联动作组合保险，具有保证膛内安全的优点；但机构整体占用空间大，不利于小型化。针对电磁轨道炮引信长时高过载的后坐环境特征以及后坐保险机构为保证膛内安全性所引起的结构尺寸偏大的问题，本文提出了应用于电磁轨道炮引信发射环境的双行程后坐-准流体延期保险机构。

1 典型的机械保险机构

一般情况下对具有发射过载大，非旋转或微旋转特点的弹药，引信保险机构设计方案常采用后坐保险机构和电火工拔销器或电磁拔销器作为执行机构的电控制保险机构组成两道保险。而电磁轨道炮发射过程中特有的膛内脉冲强磁场和炮口强电场容易对探测控制电路的电子元器件和电控执行器造成干扰和损坏，采用电控保险机构安全性和可靠性风险高，因此引信保险机构适合采用后坐保险机构、准流体延期机构和爬行保险机构等纯机械设计方案，避免膛内脉冲强磁场和炮口强电场干扰，安全性和可靠性好。

1.1 典型的双行程后坐保险机构

引信所受发射后坐过载上万g，显著区别于勤务处理中跌落环境时宜采用双行程后坐保险机构。惯性零件(如惯性筒、惯性杆等)需经过下沉和上升的往返运动后机构才能解除保险，经历的时间较长，一般在出炮口后解除保险，因而能保证膛内安全。典型的双行程后坐保险机构如图1所示,有筒式结构和杆式结构。在后坐力作用下惯性筒下沉到位释放上钢球完成解除保险过程第一阶段，而制动拴上移到位或惯性筒上移到位释放下钢球完成第二阶段。筒式结构的缺点是径向尺寸较大，因径向空间要容纳下落的钢珠(一般选用钢珠直径2.5～3 mm)，后退筒径向尺寸大，同时因保险行程小安全性也差；杆式结构简单，零件少，但为保证高安全性，保险行程必须足够大，因此轴向尺寸较大。

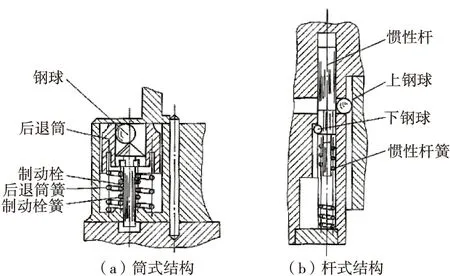
图1 典型的双行程后坐保险机构Fig.1 Typical double-stroke setback arming device

1.2 典型的后坐准流体保险机构

对于微旋或无旋转发射环境，准流体(微径玻璃珠群)延期保险机构与后坐保险结合，典型结构如图2所示。在发射环境下惯性筒下沉到位时由闭锁钢丝锁定在解保位置，从而打开泄流通道。同时珠群与活塞受后坐力在膛内并未开始泄流，钢珠依然被活塞挡住，保证膛内安全。出炮口，活塞簧作为驱动力，玻璃珠群由径向泄流，活塞上升到位时钢珠脱落释放回转体，延期保险解除[7]。

图2 非旋转式后坐-准流体保险机构Fig.2 Non-rotating setback arming and quasi-fluid delay arming device

2 双行程后坐准流体延期保险机构

电磁轨道炮引信的双行程后坐保险机构采用惯性筒式结构，通过卡环的塑性变形抗力识别发射和勤务处理环境。惯性筒受长时高后坐力使卡环发生稳定塑性变形而让位，与典型双行程后坐保险机构相比极大地减小了结构尺寸。后坐保险完全解除后才打开准流体的泄流通道，延期保险机构启动，泄流方向与爬行力一致，有利于泄流流畅。双行程后坐-准流体延期保险机构原理样机如图3所示。

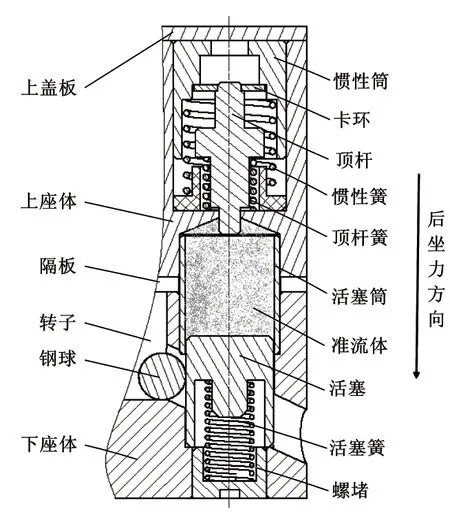
图3 双行程后坐-准流体延期保险机构示意图Fig.3 Schematic diagram of double-stroke setback arming and quasi-fluid delay arming device

双行程后坐保险机构主要由惯性筒、卡环、顶杆、惯性簧、顶杆簧和座体等组成，卡环变形抗力大，设计短的保险距离即可保证平时的安全性，缩减了保险机构尺寸，且能够产生较大塑形而不断裂失效，避免对可动件的活动造成卡滞；准流体延期保险机构主要由活塞、活塞筒、活塞簧、钢球、螺堵和座体等组成，活塞筒内容纳准流体(如微径玻璃珠群)，顶杆相当于泄流塞，出炮口时顶杆回退，打开泄流通道，泄流驱动力以弹簧内储能为原动力，同时准流体和活塞在膛内受后坐力不会泄流。

作用原理：平时，顶杆在惯性筒和顶杆簧的约束下堵住泄流孔，使准流体不能外泄，准流体控制活塞使活塞不能上升，活塞挡住钢珠，钢珠锁定被保险件(如转子)，如图3所示，爆炸序列未对正，处于隔爆安全状态；电磁轨道炮发射时，惯性筒受陡然上升的后坐力，向下挤压卡环使其发生塑性变形弯曲内收，从而脱离惯性筒内台阶面，随后，在长时后坐惯性力作用下卡环随惯性筒克服惯性簧抗力继续向下运动到位，顶杆在长时后坐力作用下依然被锁定在初始位置；当后坐力小于弹簧抗力时，顶杆随惯性筒和卡环一起返回，后坐保险解除，同时打开了准流延期保险机构的泄流通道；出炮口后，在爬行力和活塞簧推力共同作用下活塞推动准流体外泄，经历一定延时，活塞上升到一定位置钢珠由斜孔向下滚动释放转子，延期保险解除，如图4所示。

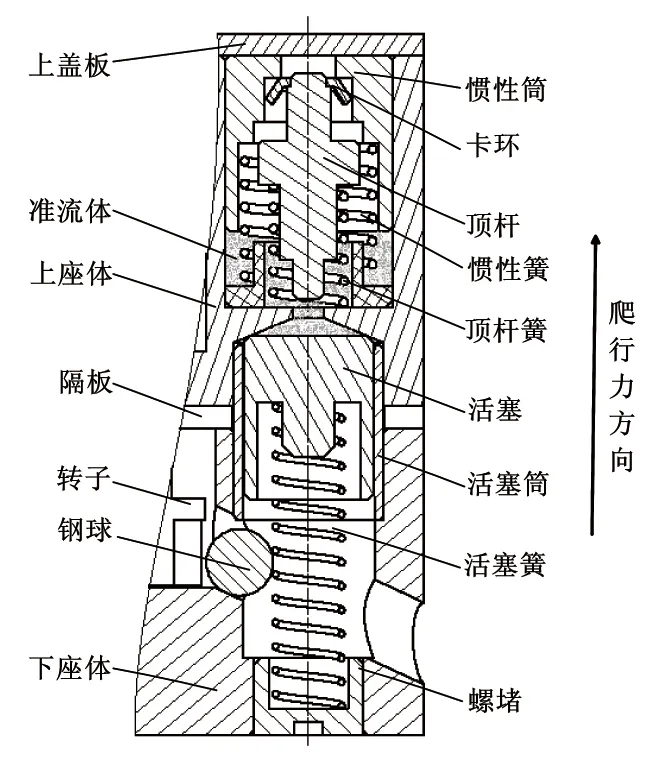
图4 双行程后坐-准流体延期保险机构解除保险后示意图Fig.4 Schematic diagram of double-stroke setback arming and quasi-fluid delay arming device after arming

3 计算仿真和试验验证

3.1 双行程后坐保险机构仿真与试验验证

电磁轨道炮采用多个电容型储能模块并联组成的高功率脉冲电源，以保证发射过程中电流波形的平稳性，放电电流接近梯形，发射过载示意图如图5所示。

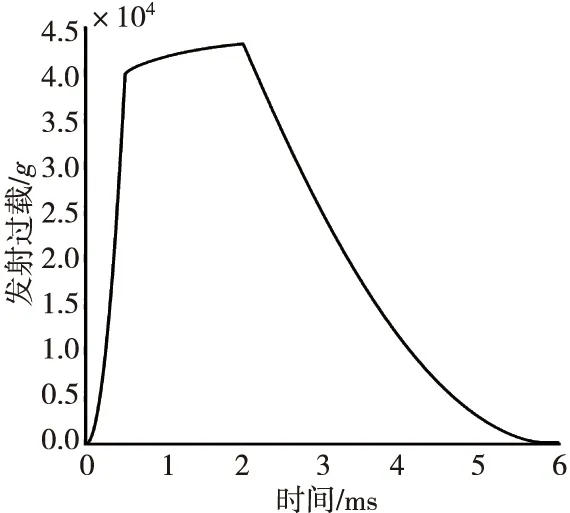
图5 电磁轨道炮发射后坐过载曲线Fig.5 The launch setback overload curve of the electromagnetic railgun

由图5可以看出后坐过载上升速度很快，平稳加速时间长，峰值达4.3万g，双行程后坐保险机构将承受长时高后坐过载。在满足解除保险可靠要求前提下需要对结构强度进行校核，防止出现薄弱零件断裂或过分变形等影响作用可靠性。卡环作为弹性抗力零件，厚度偏薄，依靠其发生塑性变形而解除对惯性筒的约束，受冲击时容易失效断裂，而断裂碎片容易造成对可动零件的卡滞，以及惯性筒下落时与座体碰撞变形是否会产生膨胀变形而卡滞不能回复，影响解除保险可靠性。

通过ANSYS/LS-DYNA软件进行动力学仿真计算，钢板跌落过载从严标准化后以正弦波形模拟，设置过载峰值为12 000g，持续0.1 ms；发射过载按图5所示数值的2/3保险系数作为设计输入，材料参数如表1所示，分析时惯性筒、卡环、顶杆、座体均采用弹性-理想塑性(各向同性硬化)带应变失效的材料本构模型。卡环采用163壳单元分析更准确，惯性簧和顶杆簧采用离散单元combi165代替，设置预压缩量以模拟实际装配情况。为减少计算量，仿真时未引入完整的容纳保险机构的座体，仅用简化带孔圆板模型代替座体底部，但不影响计算结果的准确性。

表1 材料参数Tab.1 Material parameters

仿真计算结果如图6—图 8所示。从图6可以看出跌落过载作用下0.6 mm厚卡环发生塑性变形，其根部应力最大，稍低于屈服应力，以弹性变形为主。从图7可以看出在严格的跌落过载作用下惯性筒在卡环和惯性簧的共同抗力作用下，下落一小段位移即回复，而卡环越厚，惯性筒下落位移越小，表明卡环越厚跌落时保险机构安全性越高。从图8中可以看出在跌落过载作用下卡环发生变形后随惯性筒下落0.5 mm，而惯性筒继续下落至1.1 mm即开始回复直到初始位置，顶杆位移始终在±0.1 mm范围内波动，远小于顶杆在泄流孔中堵塞尺寸2 mm，表明该双行程后坐保险机构能够保证跌落的安全性。为简化计算，惯性筒上方未设置盖板，所以回复时各部件可超过零点继续向上运动，实际情况会被盖板限位，保持在初始位置。

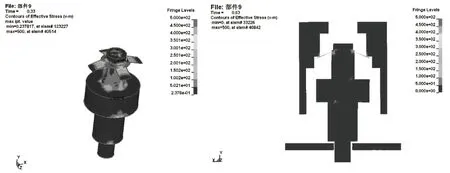
图6 0.6 mm厚卡环时跌落过程中形变及应力云图Fig.6 Deformation and stress nephogram of 0.6 mm thick clasp during dropping

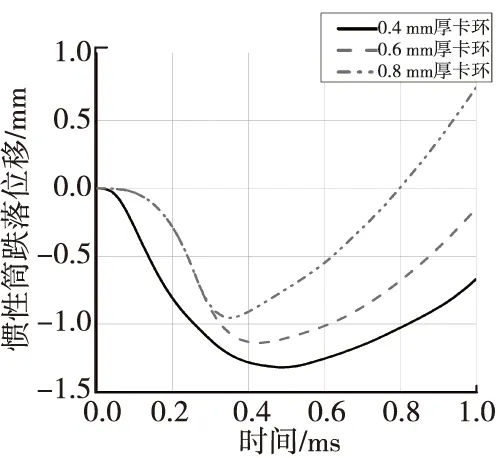
图7 不同厚度卡环对应的惯性筒跌落位移曲线Fig.7 Drop displacement curve of inertial cylinder corresponding to clasp with different thickness

图8 0.6 mm厚卡环时跌落位移-时间曲线Fig.8 Drop displacement curve of 0.6 mm thick clasp

马歇特锤击试验时可产生90 μs左右脉宽，达5万g的过载(幅值随锤重和配重变化)，一定程度上可以模拟跌落在钢板上的过载情况。对保险机构分别进行5齿(峰值约12 260g)和10齿(峰值约18 580g)的马歇特锤击试验，图9为进行10齿过载锤击后0.4 mm厚卡环的变形情况。拆解后发现卡环只有轻微塑性变形，外形尺寸只缩减了0.2 mm，与惯性筒接触处有压痕，后坐保险均未解除。

图9 峰值18 580 g过载锤击后卡环轻微塑性变形Fig.9 Slight plastic deformation of clasp after hammering with 18 580 g overload

图10所示为不同卡环厚度时惯性筒在长时高后坐过载作用下的仿真结果。

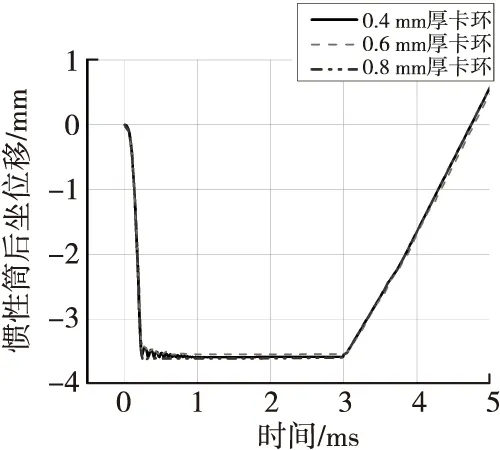
图10 后坐过载时惯性筒下落位移-时间曲线Fig.10 Falling displacement curve of inertia cylinder under recoil overload

从图10可以看出因后坐过载足够高，惯性筒下落过程并不受卡环厚度变化影响，并且在膛内始终保持在第一阶段保险解除位置；后坐过载小于弹簧抗力时，惯性筒随顶杆和卡环在弹簧抗力下回复到初始位置，第二阶段保险解除，顶杆退出泄流孔。选取惯性筒底边和中部外径上两对节点，其直径长度变化如图11所示，从图中可以看出惯性筒外径在刚接触座体时膨胀变形量低于0.005 mm，最终稳定在0.001 mm范围内，变形量很小，不影响惯性筒回复。从图12中可以看出卡环发生明显塑性变形，但未发生失效断裂，不会造成惯性筒和顶杆的运动的卡滞。

图11 惯性筒底边直径变化曲线Fig.11 Change curve of bottom diameter of inertia cylinder

图12 后坐过程中0.4 mm厚卡环和顶杆的应力云图Fig.12 Stress nephogram of 0.4 mm thick clasp and ejector bar during recoil

根据以上仿真结果，选取卡环厚度为0.4 mm和0.6 mm分别进行15齿(峰值约33 010g)和18齿(峰值约44 100g)马歇特锤击试验，模拟发射过载峰值对保险机构的影响，结果如图13所示。

图13 模拟发射过载峰值的马歇特锤击试验结果Fig.13 Results of Marshall hammer test for simulated emission overload peak

从图13可以看出：超过3万g过载后卡环产生稳定塑性弯曲变形，解除对惯性筒约束后随惯性筒下沉，过载减小到一定值后卡环和顶杆随惯性筒一起上升，后坐保险解除，试验结果与仿真结果一致。随卡环厚度增加，塑性变形程度降低，但外形尺寸变形量均大于0.8 mm，能解除对惯性筒的限制；即使超过4万g，卡环也未出现断裂或撕裂现象，无碎片，不会影响顶杆回退。随后活塞簧推动活塞向上，玻璃珠群泄流至上座体内，转子侧向挤压钢珠下落，准流体延期保险解除；同时，双行程后坐-准流体保险机构并未出现结构松动，其他刚性零件无明显变形，只有顶杆与上座体接触处有轻微压痕，机构强度满足抗过载要求。

3.2 准流体延期保险机构设计计算

电磁轨道炮无离心环境且爬行过载低，所以设计准流体保险机构主要采用弹簧驱动作为驱动力，准流体泄流方向与爬行过载一致，有利于排出。延期解除保险的过程为：顶杆退出泄流孔后，活塞簧推动活塞压迫准流体从打开的泄流孔通道流出，直到活塞上升至能够解除对钢珠的约束，钢珠沿斜孔下落，延期保险解除。准流体从泄流孔中所流出直至解除保险的时间即为延期时间。

根据经验公式及文献研究结果[5]，准流体在均匀力场中流动速率经验公式为：

(1)

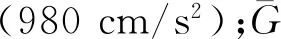
采用微径玻璃珠作为准流体，泄流出口位置在腔室中心孔处，泄流方向与活塞簧推力和爬行力同向时，将复合力场等效为恒定推力场，则式(1)在推力场的推广公式为：

(2)

式(2)中，k2=4.486，为修正系数。

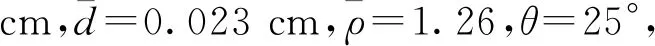
(3)

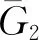
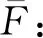
(4)

经计算，活塞簧参数为中径D=3 mm，丝径d=0.35 mm，自由高度h0=17 mm，有效圈数n=10，装配预压高度h1=6.8 mm时，延期解除保险时间可满足炮口安全距离要求。

4 结论

本文提出了应用于电磁轨道炮引信的双行程后坐-准流体延期保险机构。该机构采用惯性筒式结构，通过卡环的塑性变形抗力识别发射和勤务处理环境。惯性筒受长时高后坐力使卡环发生稳定塑性变形而让位，与典型双行程后坐保险机构相比极大地减小了结构尺寸。后坐保险完全解除后才打开准流体的泄流通道，延期保险机构启动，泄流方向与爬行力一致，有利于泄流流畅。仿真计算和实验表明，双行程后坐-准流体保险机构满足解保可靠性前提下既能够保证平时的安全性和膛内安全性，又具有延期功能保证炮口安全。