作动筒卡环受力变形计算模型研究

黄志军

(航空工业洪都,江西 南昌330024)

常用的卡环锁作动筒工作原理如图1所示,卡环锁上锁前,卡环处于压缩状态,上锁时液压推动活塞杆伸出,带动卡环沿外筒内表面滑动,当卡环移至槽口时,卡环自由胀开,卡在槽内。此时滑动活塞在液压及弹簧作用下,插入卡环内径内,限制卡环收缩,将作动筒锁在全伸长位置上。开锁时,液压推动滑动活塞克服弹簧力左移,卡环由槽中被液压推出而开锁,活塞杆收缩。

图1 卡环锁作动筒工作原理

作动筒开锁压力是作动筒重要工作性能指标,而卡环与轴或筒的配合的松紧程度影响作动筒开锁压力的大小。配合过松会使开锁压力太小,容易因回油压力而异常开锁；配合过紧会使卡环内应力超过材料自身的屈服强度,使卡环产生永久塑性变形,失去作用。为了更好的辅助卡环设计,提高设计效率,需建立了卡环受力变形计算模型,为卡环的合理设计提供依据。

1 卡环类型

卡环为一个开口弹性圆环,根据作动筒上锁时卡环的状态可将其分为两种类型:自由胀开卡环和撑开卡环。自由胀开卡环:作动筒未上锁时,卡环被外筒压缩,上锁时,卡环进入槽口后自由胀开。撑开卡环:作动筒未上锁时,卡环处于自由状态,上锁时,卡环进入卡槽被滑动活塞强行撑开。两种卡环均由滑动活塞限制其收缩而实现锁定。

2 卡环受力变形有限元仿真

利用有限元软件分别建立某自由胀开卡环和撑开卡环有限元分析模型。

自由胀开卡环接触应力如图2所示。自由胀开卡环处于压缩变形状态时,卡环外表面与外筒内表面接触,接触面上接触应力分布具有一定的集中性:开口端有较大的接触应力,分布较集中；开口对称部位偏上的较长一段圆弧部分分布着接触应力,分布规律较复杂。

图2 卡环接触应力图

撑开卡环处于变形状态时,卡环内表面与滑动活塞外表面接触,分布规律与自由胀开卡环类似。

由有限元分析计算可知,自由胀开卡环和撑开卡环在变形状态时与其它部件间的接触应力分布类似,主要集中在两个部分,故本文建立卡环计算模型时将卡环受力简化为具有对称性的4点集中载荷,如图3所示。

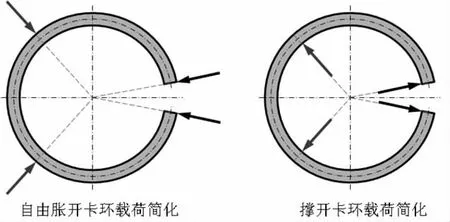
图3 简化集中载荷示意图

3 卡环计算模型建立

卡环截面简化为矩形,忽略倒角和倒圆,卡环截面厚度为h,卡环截面宽度为b,卡环单侧开口宽度为B。

图4和图5所示为卡环受力简图。由于卡环为对称结构,故图中仅绘制卡环的一半进行说明。自由状态时卡环截面中性轴曲率半径为R1,变形状态时卡环截面中性轴曲率半径为R,卡环径向变形量dr=|R1-R|。与卡环配合内(外)筒直径为D,F1和F2为卡环变形状态时的简化集中载荷,F1作用在卡环开口处。卡环处于变形状态时,F1和F2与卡环径向方向平行。αi和βi分别为F1和F2自由状态和变形状态时在卡环中性轴作用点的定位角。对于任意θ处卡环截面有3个力:轴向力F(θ)、剪力Q(θ)、扭矩M(θ)。

图4 自由胀开卡环受力简图

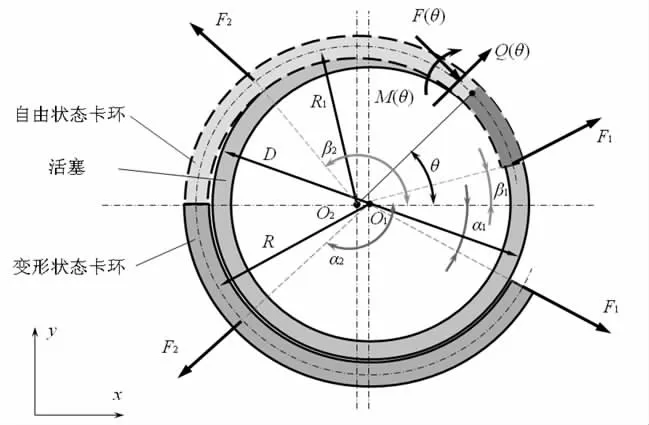
图5 撑开卡环受力简图

3.1 简化集中载荷夹角

自由胀开卡环:

撑开卡环:

3.2 应变能及简化集中载荷求解

将卡环定义为平面曲杆,c为截面形心到截面内侧边缘的距离,R0为轴线曲率半径,h为曲杆截面高度。

当R0/c=2R0/h>10时,属于小曲率曲杆,计算可近似地使用直梁公式计算；当R0/c=2R0/h<10时,属于大曲率曲杆,计算需使用曲杆公式计算。

一般情况下,卡环计算符合小曲率曲杆要求,近似地使用直梁公式计算卡环应变能。卡环受集中载荷时,任意θ处截面有3个力:轴向力F(θ)、剪力Q(θ)、扭矩M(θ),由于轴力和剪力对卡环变形的影响很小,可以忽略不计,只需考虑弯矩的影响。所以,卡环应变能

其中,s卡环中性轴轴线长度；M(s)为对应截面弯矩；E为卡环材料的弹性模量；I为卡环截面对截面中性轴的惯性矩,对于卡环矩形截面,I=bh3/12。

如图4和图5所示,假设卡环在工作状态时受到4个集中载荷:2个F1和2个F2,分别作用在角α1和α2处。不考虑卡环截面厚度的影响,根据静力平衡可得

又由于 ds=R1dθ,考虑到卡环的对称性,由式(3)、(4)和(5)可得卡环应变能

假设在卡环缺口处添加一沿y轴的单位力,则卡环θ处截面扭矩

利用莫尔积分可得单侧卡环在作用力F的作用下缺口处沿y轴方向的位移

假设在卡环缺口处添加一沿x轴单位力,则卡环θ处截面扭矩。

利用莫尔积分可得单侧卡环在作用力F的作用下缺口处沿x轴方向的位移

对于收缩卡环,根据几何关系又可求得

对于撑开卡环,根据几何关系又可求得

又卡环截面中性轴无变形,则

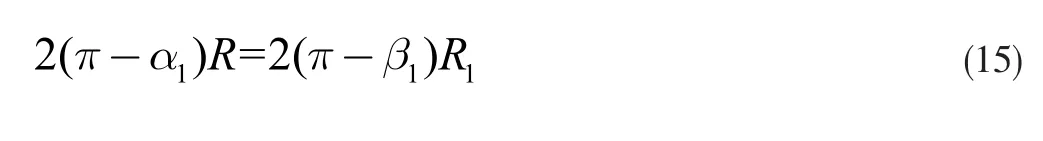
可求得

对于自由胀开卡环,由式(8)、(11)、(16)或者式(10)、(12)、(16)可求得简化集中力F1和F2。再根据式(6)可求得卡环应变能。

对于撑开卡环,由式(8)、(13)、(16)或者式(10)、(14)、(16)可求得简化集中力F1和F2。再根据式(6)可求得卡环应变能。

3.3 模型选择

由3.2 节分析可知,卡环计算时有两种方法:根据x轴位移计算和根据y轴位移计算。

计算多组实例,模型计算结果与有限元仿真结果如表1和表2所示。

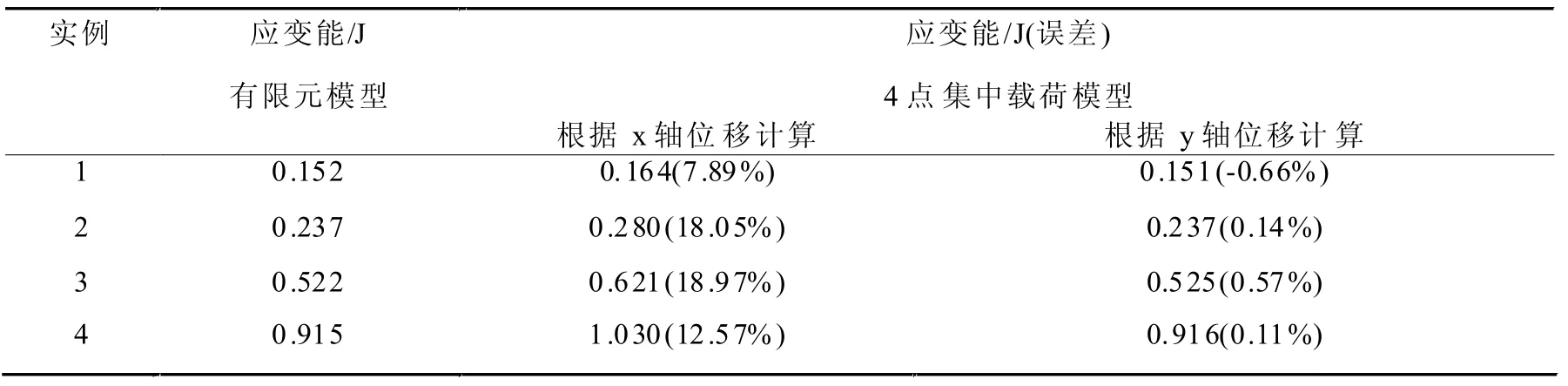
表1 自由胀开卡环计算结果对比表

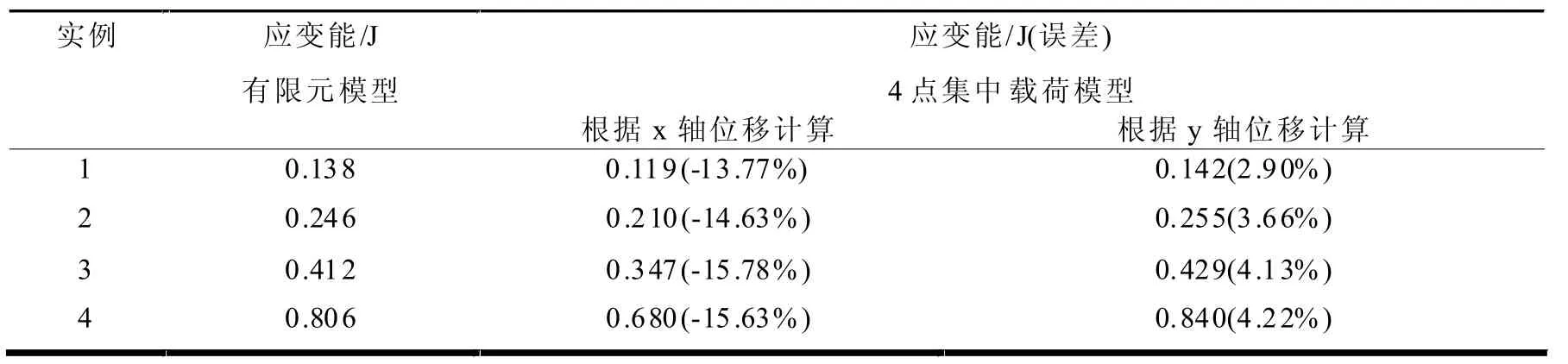
表2 撑开卡环计算结果对比表

由表1和表2可知,4点集中力模型根据y轴位移求解结果最接近仿真结果,计算误差不超过5%。所以,卡环模型计算时应根据y轴位移求解。

根据计算模型,利用Visual C#编写得到卡环计算的程序,如图6所示。

图6 卡环计算程序

4 结论

通过分析研究,主要结论如下:

4.1 通过有限元仿真分析获得了卡环受力变形时接触应力分布规律,确立了卡环建模时载荷简化为4点集中载荷。

4.2 建立了卡环4点集中载荷变形计算模型,模型计算结果与有限元仿真结果对比误差不超过5%,根据模型编写的程序可用于卡环的设计。