基于改进粒子群的重频组多目标优化算法

周仕霖

(西安科技大学，陕西 西安 710600)

0 引言

雷达的脉冲重复频率(pulse repetition frequency，PRF)是雷达波形的一个关键参数，PRF的设计将直接影响雷达的探测性能。低重频脉冲的距离数据不产生模糊，可以提供良好的测距性能，但容易产生明显的速度模糊；高重频脉冲的多普勒数据不产生模糊，可以提供较好的测速性能，但容易产生明显的距离模糊。工作在中重频模式的雷达通常循环使用若干个相参处理周期(coherent processing intervals，CPIs)，并且在这些CPIs内发射脉冲的PRF也各不相同，不同的PRF组合在一起便形成了重频组[1]。当使用重频组模式时，可以通过比较不同PRF的模糊数据实现解距离模糊和速度模糊，有效减弱杂波对探测的影响，还能提升雷达波形的抗盲区性能。因此，重频组理论在雷达波形设计中被广泛使用，重频组设计也成为雷达波形优化的重大课题。

雷达波形重频组可以从多个方面进行优化[2-3]，如解模糊、抗盲区、抗虚影等[4]。针对解模糊问题，研究人员已提出了多种解模糊算法，如重合算法(coincidence algorithm)、中国余数定理法[5]、一维集法[6]、滑窗聚类算法[7]及一系列衍生算法[8-10]。针对波形盲区问题，当前主要的研究思路是通过寻找到最优的重频组来使不同PRF的盲区交错，以减小雷达探测盲区，如遗传算法[11]、模拟退火算法[12]、蚁群算法[13]、粒子群算法[14]等。引起虚影的因素较多，如多个目标回波错误相关产生的虚影，远距离目标因噪声或杂波引起的虚影，目标自身相应延伸引起的虚影等。最优重频组不仅能完全解距离模糊和速度模糊，而且具有理想的抗遮挡性能，虚影的发生概率最小化。目前，大多数重频组优化算法的优化目标较为单一，而对多目标优化重频组的研究相对较少。

本文针对传统目标优化算法存在优化目标较为单一的问题，提出一种基于改进粒子群的重频组多目标优化算法，以解模糊、抗盲区、抗虚影为目标，综合设计重频组，实现了雷达脉冲重频组的多性能优化。

1 雷达重频组能力分析

1.1 解模糊能力分析

如果PRF给定，则其最大不模糊距离：

(1)

式(1)中，c=3×108m/s为光速常量，fr为PRF的具体数值。最大不模糊速度：

(2)

式(2)中，λ为发射波束的波长，此处Vmu为实际值的绝对值。定义波束的不模糊探测空间为Rmu和Vmu，即：

(3)

由式(3)可知，当波束波长参数确定时，该波束的不模糊探测能力即为定值，Smu在期望距离和速度的探测二维空间上平铺展开，即可得到该波束的探测模糊图，如图1所示。

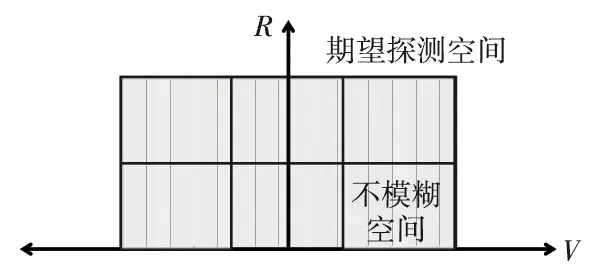
图1 不模糊空间在期望探测空间上平铺示意图Fig.1 Schematic diagram of the tiling of the non-blurring space on the desired detection space

波束重频组设计的首要问题为期望探测空间解模糊。为能够解距离模糊和速度模糊，重频组在设计时有两个基础的约束，即：

(4)

LCM(PRF1,PRF2,…,PRFN)≥fdmax

(5)

式(4)、式(5)中，LCM为求最小公倍数运算；PRI为脉冲重复间隔(pulse repetition interval)，其与PRF互为倒数；Rmax为雷达的最大探测距离；fdmax为最大多普勒偏移频率；M为解模糊所需最少PRF数目；N表示重频组中PRF总数目。M和N的设定通常可由M/N准则得到，典型的M/N为3/8组合，即8个重频组中只要在任意3个重频下检测到目标存在，即上报目标。由此可知在3/8组合下共有56种重频搭配。由式(4)和式(5)可得每种搭配的解模糊距离和解模糊速度。只有当所有搭配的解模糊距离和解模糊速度均大于期望的探测距离和速度时，重频组才能在探测空间内完全解模糊。

1.2 抗盲区性能分析

中重频脉冲在探测时除距离盲区和速度盲区外，副瓣杂波、杂波、噪声等因素也会造成探测盲区，为了简化计算，本文仅考虑距离盲区和速度盲区两个主要因素。

图2为在距离和速度两个维度上，单重频组成的盲区。由于距离模糊和速度模糊的存在，单重频波束的盲区分别在距离和速度维上延伸，在盲区图上形成网格状分布。当目标处于图中的黑色区域时，雷达或正在进行脉冲发射，或将接收到的波束频段进行抑制，无法对目标进行有效探测。

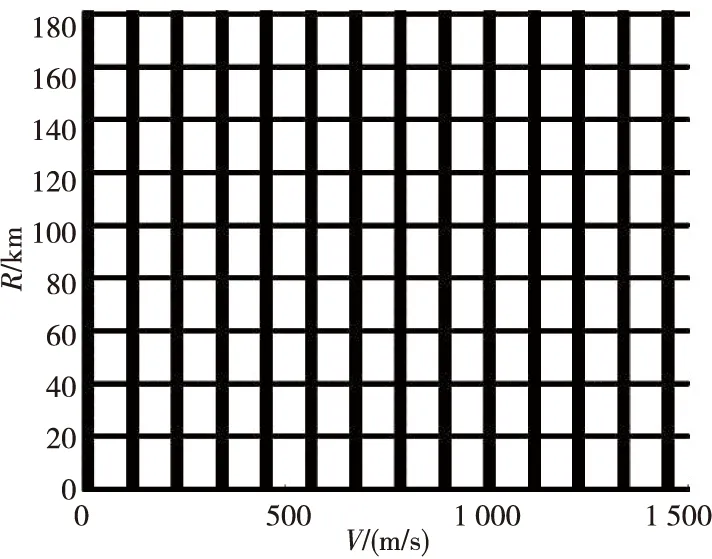
图2 单重频盲区延伸示意图Fig.2 Schematic diagram of single frequency blind zone extension

通过重频组优化，可以大幅减小雷达的距离盲区和速度盲区，大幅提升探测区域内的波束非盲区区域，如图3所示。

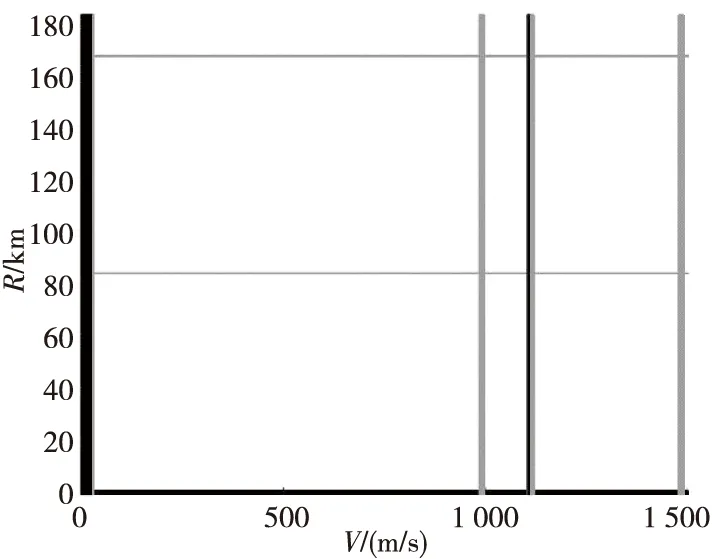
图3 重频组优化后盲区示意图Fig.3 Schematic diagram of blind area after optimization of repeated frequency group

1.3 抗虚影能力分析

虚影的产生方式主要有两种：一种是由于目标的回波在距离单元或速度单元上出现了延伸，跨越了两个或数个单元，以至达到检测门限的回波数量，即达到报告的要求，上报虚假目标；另一种是对目标的模糊回波在M个PRF下进行了错误的相关，以致在特定的距离或速度上出现虚假目标。

在设计重频组时，保持较大的解模糊余量可以有效减少第一种方式引起的虚影。解模糊余量在探测空间上是波动的，只有在探测空间上的最小解模糊余量满足要求时，才能保证其在所有探测空间上均降低虚影发生的概率。

在保证最小解模糊余量满足要求的前提下，本文主要对第二种虚影问题进行优化。此种方式的虚影产生机制如图4所示，目标1、目标2、目标3的回波在3个PRF中对准，均为真实目标。当不同目标的回波在某一单元内对准时，系统同样上报发现目标，此目标为回波错误相关所致。如果有K个目标，则参与相关过程的M个PRF得到可能目标的数目为KM，并且这些可能目标分布于M重频的解模糊空间内。

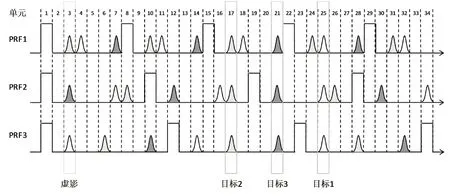
图4 错误互相关产生虚影示意图Fig.4 Schematic diagram of false cross-correlation resulting in shadow

如图5所示，当真实目标个数一定时，对于服从3/8准则的重频组，可能的相关结果数目是确定的KM，而最大解模糊空间却不尽相同。

图5 最大解模糊空间对虚影产生概率影响示意图Fig.5 Schematic diagram of the influence of maximum deblurring space on the probability of shadow

在可能的相关数目一定的前提下，最大解模糊空间越大，可能的虚影存在于期望探测空间内的概率就越小。因此，为了减少因目标回波错误相关造成的虚影，在保证重频组解模糊余量满足要求的前提下，可以通过扩大重频组对应的最大解模糊空间来降低虚影发生率。

2 基于改进粒子群的重频组多目标优化算法

本文通过构建多目标优化模型，在传统粒子群算法基础上，通过混沌理论对粒子群算法进行改进，大幅提升了初始粒子种群的随机性和遍历性，从而加速种群向最优解收敛。

2.1 多目标优化模型构建

本文对重频组的优化目标主要有两个：

1)提高重频组的抗盲区能力，提高在期望探测空间内非盲区区域的比例；

2)扩大重频组最大解模糊空间，降低因回波错误引起的虚影发生率。

重频组在重频组关注区域内非盲区区域(即可视区域)的占比，即图3中空白部分占全部空间的比例，可通过如下过程判定得出：

1)计算重频组内每个PRF的不模糊距离和不模糊速度，并转换为距离单元的个数；

2)根据脉宽和多普勒抑制带宽计算发射遮挡的距离单元和速度单元数；

3)将重频组不模糊空间按照不模糊距离和不模糊速度间隔，铺满整个关注探测空间；

4)将关注探测空间根据距离单元和参考速度单元完全划分为网格；

5)在每一个网格上进行盲区判定；

6)判定完所有网格后，将可视网格除以所有关注网格。

R和V分别为重频组最大解模糊距离和最大解模糊速度，在3/8重频组中，解模糊所需的最少重频数为3个，因此8个重频共有56种组合，每种组合都可通过求解最小公倍数计算(即式(4))得到可以完全解模糊的最大脉冲重复周期(PRI)。这个PRI可以计算得到最大不模糊距离Rmax，即为R，以及最大不模糊速度Vmax，即为V。通过上述方法，便能够计算出Rmax与Vmax的56种组合，则重频组的最大解模糊距离R和最大解模糊速度V便为这56种组合中Rmax和Vmax的最小值。

式(4)和式(5)为重频组需满足的最低条件，而R和V则是该重频组能够达到的最高条件，如果超过R和V，该重频组将不能解模糊。一般R和V的计算结果非常大，完全能够满足关注探测范围的要求。但最大解模糊空间内产生虚影的总数一定，若最大解模糊空间变大，则虚影落在关注探测空间内的概率就会降低，即虚影发生的概率将会减小。

1)目标函数

在对重频组进行多目标优化时，适应度函数的设计将直接影响算法的收敛速度和效果。本文所提算法的适应度函数如下：

f=ω1S+ω2Rdmax+ω3Vdmax

(6)

式(6)中，f为粒子的适应度；S为重频组得到的非盲区区域占期望探测空间的比例；Rdmax、Vdmax分别为重频组的最大解模糊距离和最大解模糊速度；ω1、ω2、ω3为上述三个优化目标的权重值，通过大量的实验确定，本文取值分别为0.6、0.2、0.2。

2)约束体条件

PRF的上下限的确定方案有多种，本文选取了较为典型的确定方式。

由于已设定了占空比上限，且脉宽固定，那么PRI的下限即可确定，计算公式即为：

PRId=τ/dcycle

(7)

如果PRI小于下限，那么占空比将超过20%；PRI的下限与PRF的上限意义相同。

本文多普勒抑制带宽占多普勒带宽的比例选用最为典型的50%占比。多普勒带宽通常为PRF，因此PRF的下限为：

(8)

式(8)中，bps为带宽，dsb为多普勒抑制带宽。

通过式(7)和式(8)及PRI与PRF转换公式，可得PRF上下限。

2.2 改进粒子群多目标优化算法

粒子群算法(particle swarm optimization，PSO)[15-16]虽然具有高效的搜索能力，但其种群初始化为随机性初始化，在计算机计算中，随机数的生成只是一个伪随机过程，与时间等一些列因素有关，生成的数据虽然在庞大的数量中可能表现为均匀分布，但是在实际应用中数据量并不可能达到这种等级的数量，因此PSO存在遍历性较差，在迭代后期很容易失去粒子多样性，陷入局部最优的问题；Logistic映射具有良好的类随机、非周期、对初始值敏感、历经各态并可确定等特性。

Logistic映射生成序列的概率密度分布函数为：

(9)

由序列的概率密度函数可得序列的期望为：

(10)

自相关系数为：

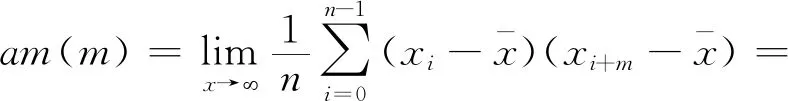
(11)

可见Logistic映射生成的序列中各元素之间的相关性为0。因此，若以Logistic映射对PSO初始种群进行处理，能够增加初始种群的随机性和遍历性，对算法收敛速度有积极意义。

本文通过混沌理论[17-18]对粒子群进行初始化，以提高粒子群的随机性和遍历性，此处采用Logistic映射[19-20]对种群进行初始化：

ci+1=μci(1-ci),μ∈[0,4]

(12)

式(12)中，μ为控制参数，当μ确定后，给定一个c0∈(0,1)，根据式(12)即可得到一个序列{c1,c2,…，cn}。不同的μ和c0得到的序列不同，且差别较大。当3.569 945 6≤μ≤4且c0∉{0.25,0.5,0.75}时，Logistic映射会呈现混沌状态。

根据Logistic映射对初始种群进行混沌化，需要对生成的混沌序列进行变换：

xi=ci×t+ld,i=1,2,…,n

(13)

式(13)中，ci为混沌序列中的元素；t为PRF组的数量级变化参数；ld为PRF选择范围的下限值，n为重频组内PRF数目，在3/8准则下，n=8。根据式(13)形成初始种群，即可改善PSO在解空间内的遍历性和随机性。

3 仿真验证

3.1 算法参数设置

为验证本文所提算法的性能，本文以某雷达系统为基础，根据其参数进行仿真环境设计，仿真平台配置具体如下：CPU为RTX2060，内存为32 G，计算机型号为联想拯救者Y7000P，仿真语言为Python。雷达系统的参数如表1所示。

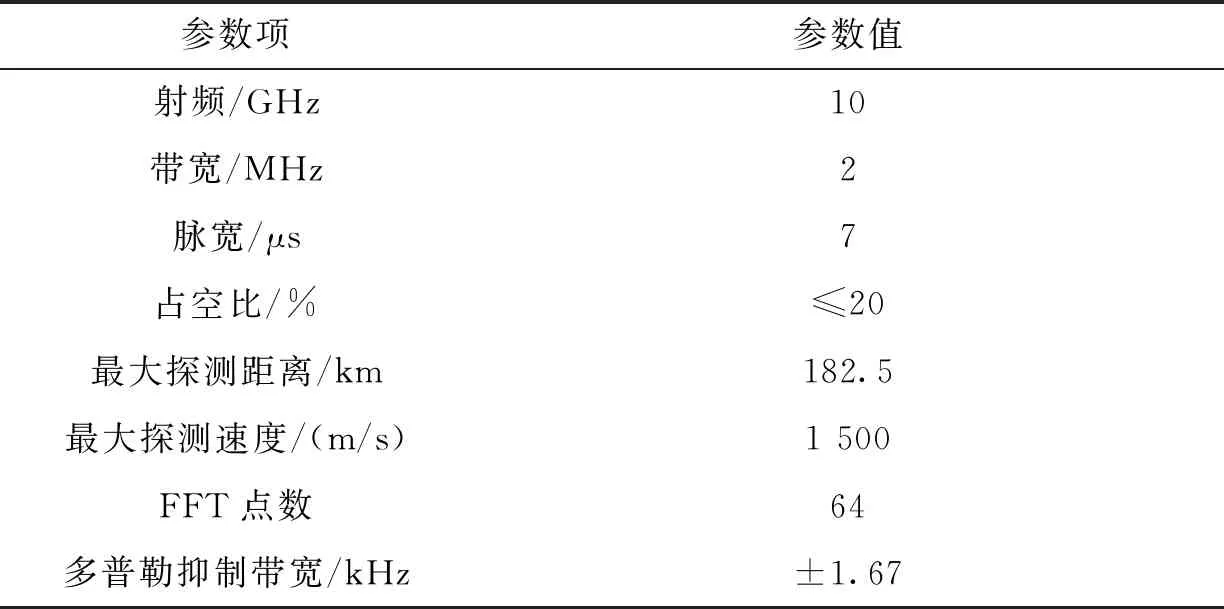
表1 雷达系统参数表Tab.1 Table of radar system parameters

通过表1数据计算可知，雷达PRI下限PRId=τ/dcycle=7/0.2=35 μs，对应PRF上限为PRFu=1/PRId=28 571 Hz；设定dsb不超过bps的50%[1]，则PRF的下限为PRFd=2×1.67×103/0.5=6 667 Hz，对应的PRI的上限为PRIu=1/PRFd=150μs。

根据PRF的范围设置粒子群算法的初始种群，设定种群数量为50，最大迭代次数为100，最小误差为1×10-10，w、c1、c2分别设置为0.8、0.5、0.5，仿真设定目标数量为3个，位置边界即为PRF的上下界，速度边界设置为每个维度的10%。

3.2 仿真结果分析

本文对改进PSO算法进行了多次仿真实验，对得到的重频组的相关性能进行了评估分析。为了验证所提算法，本文以传统PSO算法作为对比，进行对比试验。

两种算法得到的重频组非盲区区域比例如图6所示。当采用改进PSO算法进行优化时，重频组非盲区区域比例在97%左右，在实验中得到的最高比例为97.42%；当采用传统PSO算法进行优化时，重频组非盲区区域比例在94.5%左右，在实验中得到最高比例只能达到95.16%。综合来看，本文提出的改进PSO算法明显优于传统PSO算法，能较好地减少盲区比例。

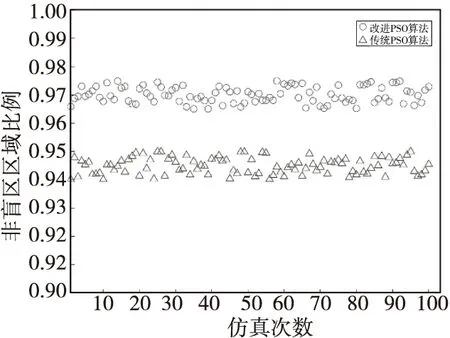
图6 两种算法的非盲区区域比例对比图Fig.6 Non-blind area ratio comparison diagram of the two algorithms

两种算法所得重频组在期望探测范围内虚影数目分布如图7所示。由图可知，两种算法在出现虚影数目上存在着明显差别。传统PSO算法得到的重频组虚影数普遍高于改进PSO算法得到的重频组虚影数，即改进PSO算法抗虚影能力优于传统PSO算法。

图7 两种算法虚影数目对比图Fig.7 Comparison diagram of the number of the two algorithms

由图8与图9可知：改进PSO算法所得重频组最大解模糊距离最小值为11 167.816 km，平均值为5 261 706.316 km；最大解模糊速度最小值为11 167 815.818 m/s，平均值为5 261 706 316.087 m/s；传统PSO算法最大解模糊距离最小值为2 916.065 km，平均值为2 412 941.539 km；最大解模糊速度最小值为1 448 384.711 m/s，平均值为2 138 723 433.426 m/s。因此，改进PSO算法所得重频组最大解模糊距离和最大解模糊速度值均大于传统PSO算法，即改进PSO算法寻优能力更强。

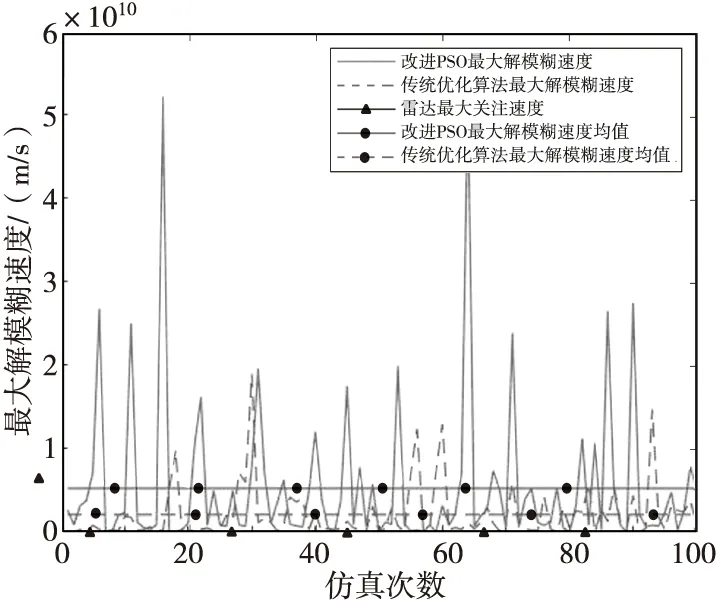
图8 最大解模糊速度对比曲线图Fig.8 Comparison curve of maximum blur resolution speed

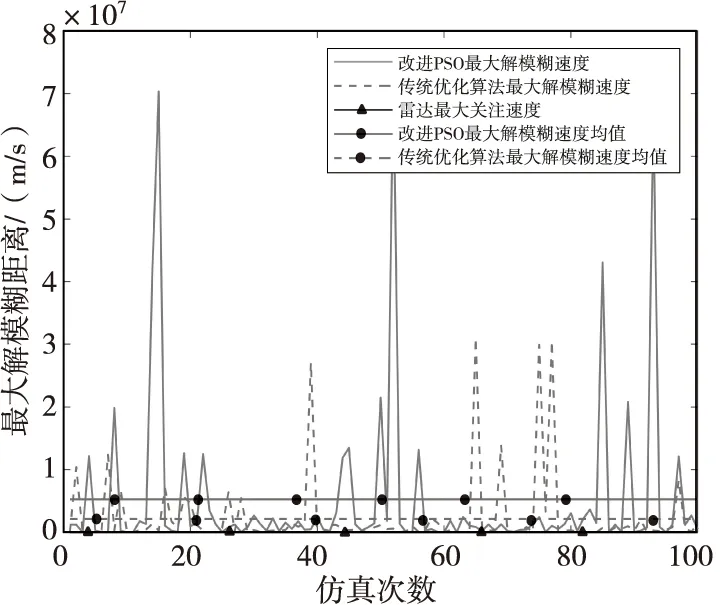
图9 最大解模糊距离对比曲线图Fig.9 Comparison curve of maximum blur resolution distance

4 结论

针对传统目标优化算法存在优化目标较为单一的问题，本文提出了基于改进PSO的重频组多目标优化算法。仿真实验验证结果表明，该算法能将非盲区比例从95.16%提升至97.42%，最大解模糊距离从2 412 941.539 km增至5 261 706.316 km，最大解模糊速度从2 138 723 433.426 m/s增至5 261 706 316.087 m/s，可有效提升雷达系统的抗盲区、解模糊和抗虚影性能。但本文算法在进行参数选取时未实现自适应，有待进一步改进。