基于变分模态分解的侵彻过载信号特征提取

张晨阳，张 亚，李培英，李世中，赵海峰

(1.中北大学机电工程学院，山西 太原 030051;2.邯郸学院，河北 邯郸 056005;3.南京信息职业技术学院机电学院，江苏 南京 210023)

0 引言

弹体在侵彻弹靶过程中产生的减加速度称为侵彻过载信号[1]。侵彻过载信号的成分复杂，不仅包括由弹体和弹靶的应力作用产生的刚体加速度，还包括弹体的振动响应、弹靶的应力波响应以及噪声等干扰信号[2]。因此，分析侵彻过载信号的首要任务在于寻找一种有效的信号特征提取方法，滤除侵彻过载信号中的干扰信号，提取到仅由应力作用产生的侵彻过载信号[3-4]。

文献[5]采用机械滤波的方法在压电传感器的两端加入减震片，只能滤除指定频率范围的干扰信号，无法提取出叠加在弹体上的频率响应。文献[6]采用小波分解法，相对完整地保留了侵彻过载信号中的波峰部分和突变部分，但该方法只能表征以低频信号为主要成分的信号特性，不能有效分解包含大量细节信息的信号，并且其算法本身缺乏自适应性,容易受到小波基函数、分解层数以及阈值的影响。文献[7]采用小波包分解法，对分解后的高、低频分解系数继续分解，得到了更精确的频谱成分以及更多频段信号所包含的信息。文献[8]采用经验模态分解(empirical mode decomposition,EMD)循环筛分的方式实现了信号的有效分解，但EMD以包络线分解结束作为判断标准，缺乏理论支撑，且多次递归分解会放大包络估计误差，容易出现模态混叠和端点效应问题。集合经验模态分解和完备集合经验模态分解在一定程度上解决了EMD的模态混叠问题，但同时加大了算法计算量，且仍未解决端点效应问题[9-10]。文献[11]根据变分思想和维纳滤波器提出一种非递归式变分模态分解(variational mode decomposition,VMD)算法，该算法的循环迭代过程是在变分模型的约束下进行，通过求取有限变分模型的最优解，确定每个本征模态函数的中心频率和带宽，然后根据输入信号的频域特征，实现信号各频率成分的自适应分解[12-13]。该方法目前已实际应用于轴承故障诊断、生物组织识别诊断、复杂信号分析处理等方面[14-15]。针对传统侵彻过载信号处理方法存在滤波效果不佳、模态混叠、端点效应、自适应性差的问题，本文提出基于变分模态分解的侵彻过载信号特征提取方法。

1 VMD理论

VMD是基于维纳滤波、希尔伯特变换与解析信号、频率混合等理论基础提出的一种信号分解方法，以寻找变分模型的最优解为目标，将信号自适应地分解为有限个具有稀疏特性的模态函数。

1.1 维纳滤波

含有高斯白噪声的时域信号表达式如下：

f0=f+n

(1)

式(1)中，f0为观测信号，f为原始信号，n为均值为0的高斯白噪声。

从含噪的观测信号中恢复出原始信号是一个病态逆问题，可采用Tikhonov正则化求解，即构造式(2)：

(2)

式(2)中，α为高斯白噪声方差，∂tf为f对t求偏导。利用欧拉-拉格朗日方程可将式(2)化为：

(3)

通过傅里叶变换，得到上式在频域内的解为：

(4)

原始信号f是观测信号f0在ω=0附近的低通窄带，因此维纳滤波器对信号具有一定的降噪能力。除此之外，维纳滤波器对信号还具有一定的约束能力，为建立VMD算法中的约束变分模型奠定了基础。

1.2 希尔伯特变换与解析信号

设f(t)为一个连续的时间信号，其希尔伯特变换定义为：

(5)

式(5)中，H算子表示希尔伯特变换，f(t)的希尔伯特变换为f(t)与1/πt的卷积，表明希尔伯特变换所得结果为线性时不变系统的输出。系统的脉冲响应h(t)=1/πt，对应的傅里叶变换见式(6)，因此希尔伯特变换可视为一个全通滤波器。

(6)

希尔伯特变换常用于构造实信号的解析信号。设信号f(t)为实信号，其复数解析信号定义为：

fA(t)=f(t)+jHf(t)=A(t)ejφ(t)

(7)

式(7)中，A(t)为振幅，φ(t)为相位。VMD中模态函数的振幅变化缓慢，根据Bedrosian定理，可将解析信号化为：

uk,A(t)=Ak(t)[cos(φ(t))+jsin(φ(t))]=
Ak(t)ejφ(t)

(8)

解析信号的单边频谱仅由非负频率组成，因此可通过求解析信号的实部恢复出原始实信号。

f(t)=R{fA(t)}

(9)

1.3 频率混合

频率混合是指在处理多个不同频率的非线性信号时，分析结果中出现频率交叉项的现象。设两个非线性信号的频率分别为ω1和ω2，二者相乘结果如下：

2cos(ω1t)cos(ω2t)=
cos[(ω1+ω2)t]+cos[(ω1-ω2)t]

(10)

在输出端得到两个混合频率ω1+ω2和ω1-ω2。同样，用解析信号表示可得：

ejω1tejω2t=ej(ω1+ω2)t

(11)

而在傅里叶变换域中有：

(12)

由式(12)可知，在复频域中，解析信号与纯指数函数相乘相当于发生了频移。

2 基于VMD的侵彻过载信号特征提取方法

VMD将侵彻过载信号f(t)分解为有限个具有固定带宽的本征模态函数，以每个本征模态函数及其中心频率附近的窄带信号构造变分模型，通过交替方向乘子法在其频域内迭代求解，将f(t)分解为各本征模态函数的线性组合。

2.1 构建变分模型

在VMD中将本征模态函数定义为一组调幅-调频信号，表达式如下：

uk=Ak(t)cos(φk(t))

(13)

式(13)中，Ak为本征模态函数的瞬时振幅，φk是相位，对相位求导可得瞬时频率ωk(t)。

ωk(t)=φ′k(t)

(14)

为了使本征模态函数既能最大化包含侵彻过载信号中的有用信息，又具有一定的稀疏度，将本征模态函数看作幅值为Ak，频率为ωk(t)的正弦波，并通过以下3步建立变分模型：

1)对每个本征模态函数进行希尔伯特变换，求出相应的解析信号，获得单边频谱：

(15)

2)为每个本征模态预估一个中心频率ωk(t)，将各模态解析信号的频谱搬移至基带：

(16)

3)计算解调信号的H1高斯平滑度即梯度的平方范数，估算各本征模态函数的带宽，建立变分模型。

(17)

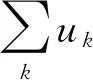
2.2 求解变分模型

为了将求解变分模型最优解的约束变分问题转化为非约束变分问题，引入二次惩罚因子α和拉格朗日乘子λ(t)，表达式如下：

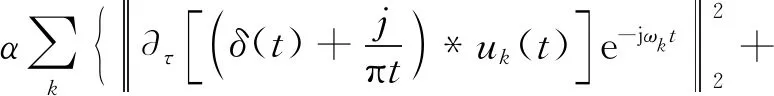
(18)

采用交替方向乘子法求解增广拉格朗日函数的鞍点uk和ωk，即为该非约束变分问题的解。求解uk和ωk的具体步骤如下：

1)求解uk。将式(18)中的非约束变分问题转化为uk最小化问题。

(19)

在傅里叶域内采用L2范数下的Parseval/Plancherel傅里叶等距求解式(19)。

(20)

将式(20)中第一项的ω替换为ω-ωk，结果如下：

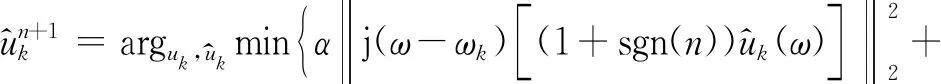
(21)

利用重构保真度项中实信号的厄米特对称性，将式(21)改写成积分形式：

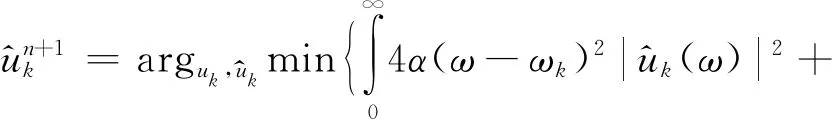
(22)

可得uk最小化结果如下：

(23)

2)求解ωk。由于中心频率ωk不包含在重构保真项中，可将式(18)化简如下：

(24)

与uk的求解过程相同，对式(24)在傅里叶域内进行求解：

(25)

可得ωk最小化结果如下：

(26)

拉格朗日乘子的迭代计算结果如下：

(27)

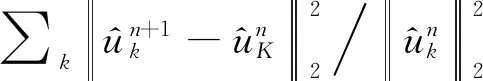
2.3 重构侵彻过载信号

重构信号不仅要最大程度地保留侵彻过载信号特征，而且要去除侵彻过载信号中的干扰信号。为此引入均方误差μ和曲线光滑度ρ两个参数构造目标函数，判断各重构信号的特征提取效果，以确定重构信号，目标函数如下：

η=a×μ+(1-a)ρ

(28)

式(28)中，η为提取效果，a为比例系数。

3 侵彻实验及结果分析

3.1 侵彻实验

为了获取弹体侵彻过载信号，使用如图1所示的弹载测试系统进行侵彻过载实验。实验流程如下：首先将弹载测试系统安装在实验弹体底部，在侵彻实验中由加速度传感器测得弹体侵彻振动信号；然后振动信号经信号处理器放大、滤波后，传送到模数转换器中进行模数转换并存储到数据存储器中；在实验结束后，通过测试系统的数据接口将数据读取出来。实验测得的弹体侵彻过载信号曲线如图2所示，测得弹体侵彻深度为100.42 cm。侵彻实验效果如图3所示。

图1 弹载测试系统Fig.1 Bomb test system

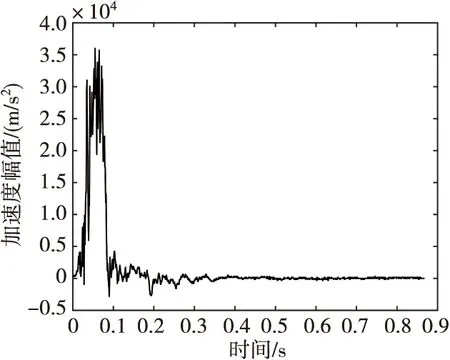
图2 弹体侵彻过载信号曲线Fig.2 The projectile penetrates the overload signal curve

图3 侵彻实验效果Fig.3 Penetration experiment effect

3.2 实验信号变分模态分解

以1 kHz作为采样频率对侵彻过载信号进行变分模态分解。由于信号分量个数未知，为确定本征模态函数分解个数K，将各本征模态函数的中心频率按从低到高排列，并观察其中心频率曲线的变化结果如图4所示，为了使图像显示更加明晰，对X坐标轴使用对数坐标。

由图4可知，K取9时本征模态函数的中心频率曲线没有重叠且高频部分间隔较为均匀；K取10时中心频率曲线在高频部分间隔较近，容易发生重叠，所以K取9。K取9时，各本征模态函数图像如图5所示。

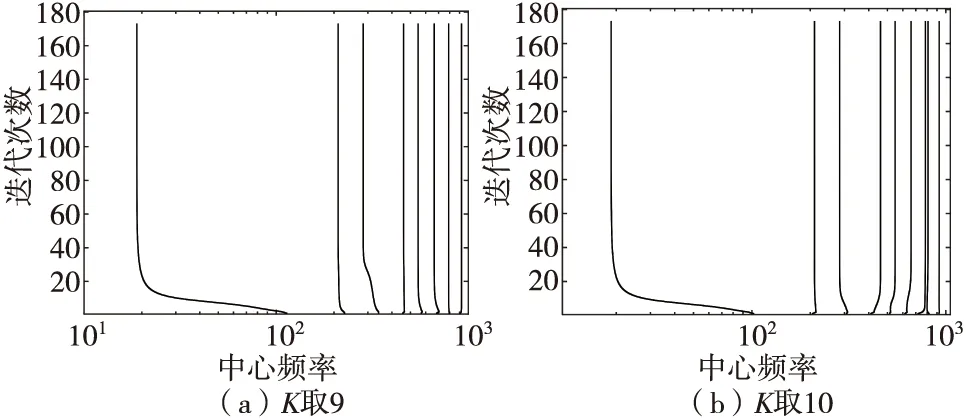
图4 中心频率变化曲线Fig.4 Center frequency curve

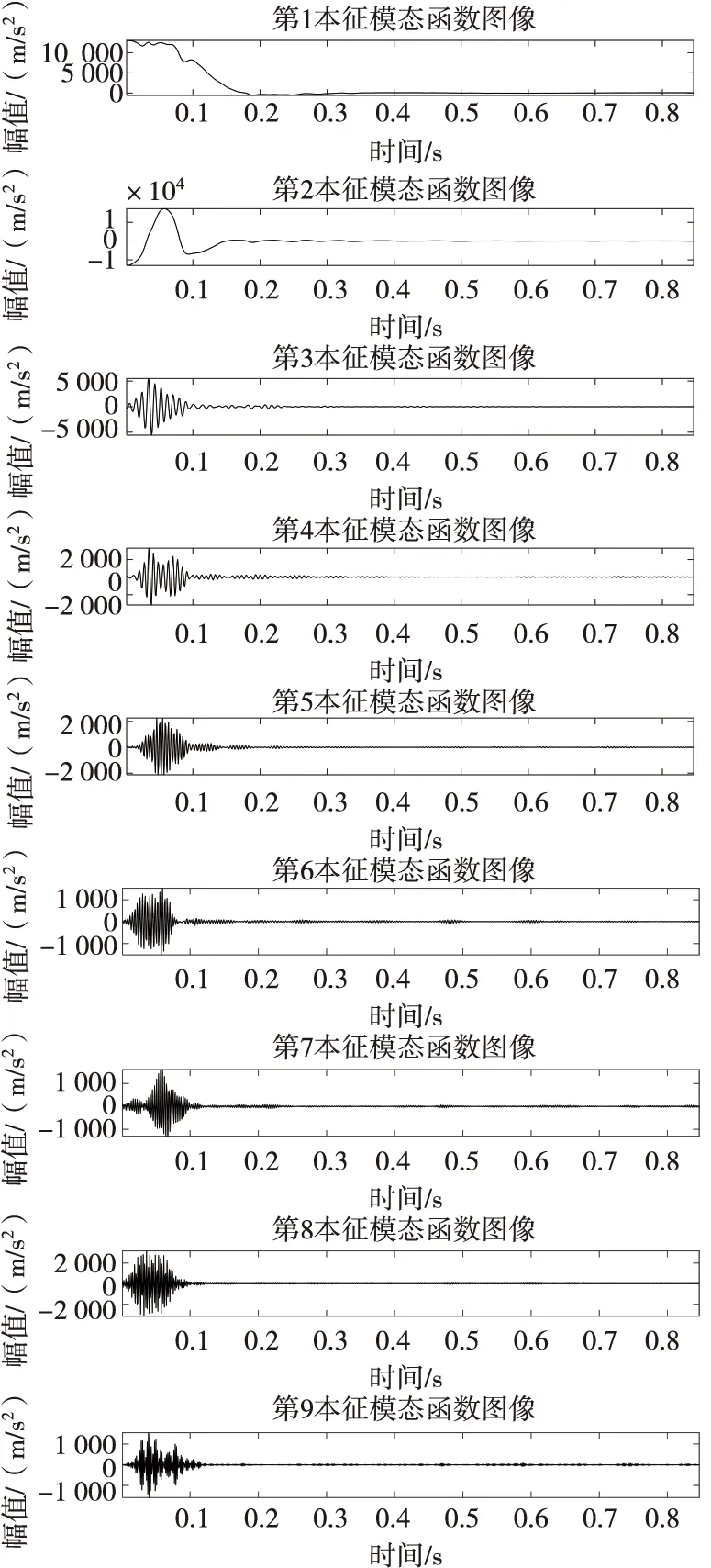
图5 各本征模态函数图像Fig.5 Images of each eigenmode function

3.3 重构侵彻过载信号

为了去除变量间的量纲关系，使数据具有可比性，对计算的均方误差和曲线光滑度进行标准化处理，同时为了使重构信号兼顾保留侵彻过载信号特征及去除侵彻过载信号中的干扰信号，式(28)中的a取0.5。均方误差、曲线光滑度及目标函数图像如图6所示。

由图6可知，目标函数在第2个重构信号处的计算结果最低，即第2个重构信号的重构效果在9个重构信号中为最佳，因此取第2个重构信号作为VMD重构信号。VMD重构信号波形图及误差如图7所示。

图6 均方误差、曲线光滑度及目标函数曲线Fig.6 Mean square error,curve smoothness and objective function curves

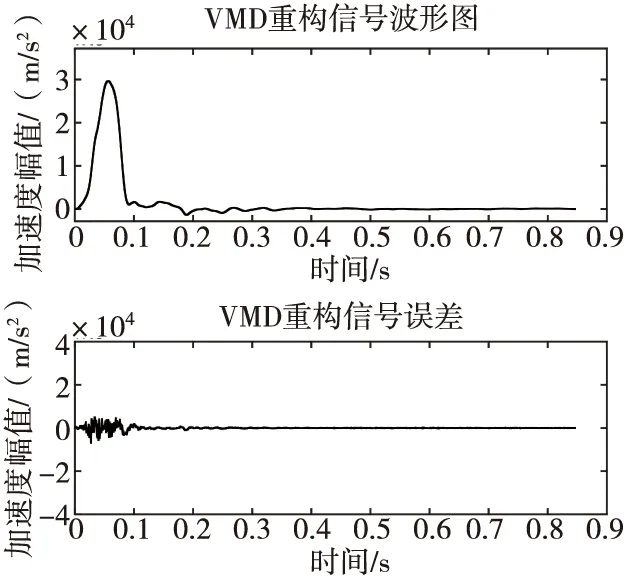
图7 VMD重构信号波形图及误差Fig.7 VMD reconstruct signal waveform and error

3.4 实验结果分析

为了验证VMD处理侵彻过载信号的可行性和有效性，采用EMD处理同一侵彻过载信号，得到两种处理方法下的重构信号波形对比图如图8所示。

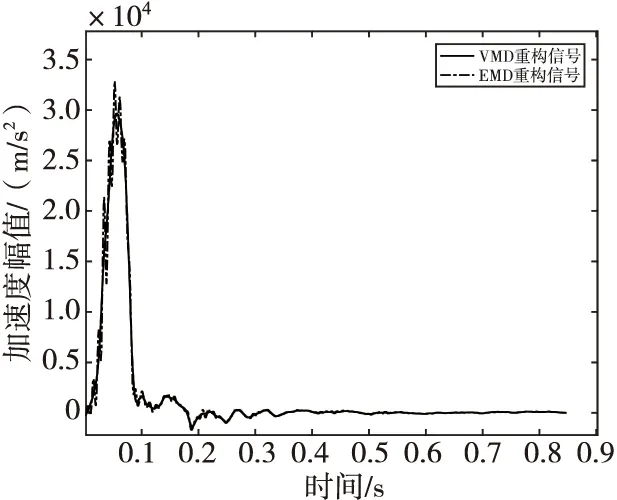
图8 两种方法重构信号波形对比图Fig.8 Two methods of reconstructing signal waveform contrast diagram

由图8可知，VMD重构信号在保留侵彻过载信号数据特征规律的同时，信号曲线更为光滑。为了进一步比较二者的特征提取效果，一方面计算两个重构信号的信噪比，另一方面对两个重构信号在时域内进行二次积分，计算弹体的侵彻深度(见图9)并与实际侵彻深度比较，计算结果见表1。

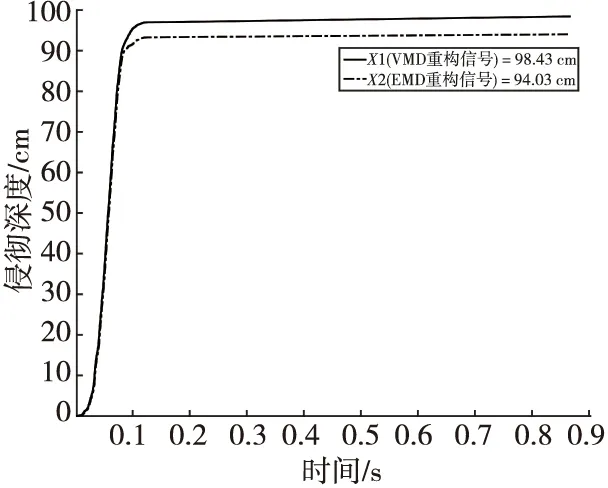
图9 重构信号侵彻深度曲线Fig.9 Reconstruct the signal penetration depth curves

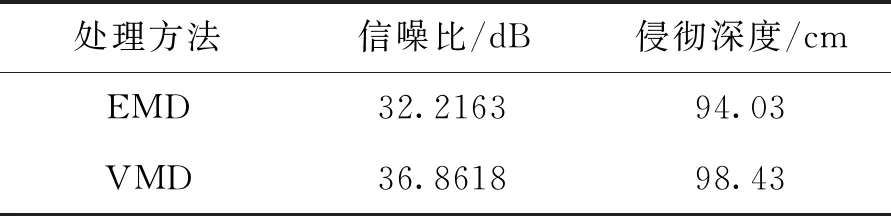
表1 两种方法的处理效果Tab.1 The treatment effect of two methods

由表1可知，VMD重构信号的计算侵彻深度为98.43 cm与实验测得的弹体侵彻深度100.42 cm更为接近，且VMD重构信号的信噪比更高，因此VMD比EMD更具可行性和有效性。

4 结论

本文提出了基于VMD的侵彻过载信号特征提取方法，该方法将侵彻过载信号的特征提取过程转移到变分框架内进行处理，通过寻找变分模型的最优解获取本征模态函数，能够自适应地实现信号的频域划分和各分量的有效分离，并有效地提取出侵彻过载信号的数据统计特性，在分析处理非平稳、非线性、多尺度的信号中具有优良的噪声鲁棒性。通过处理实验测得的侵彻过载信号，验证了VMD方法的可行性和有效性，与EMD的处理效果对比，得出以下结论：

1)相比于EMD，VMD在侵彻数据的事后处理方面对噪声具有更好的抑制作用且重构信号的积分侵彻深度更接近实验侵彻深度；

2)VMD在保留原始信号变化趋势的基础上有效地去除了高频噪声，提高了重构信号的曲线光滑度，有助于进一步分析信号的数据统计特性；

3)VMD为研究侵彻实验中的侵彻数据事后处理提供了新方法，通过分析处理提取出的重构过载信号，获得重构过载信号的数据统计特性，挖掘其中蕴含的深层信息，进而分析弹体的侵彻过程，对弹体强度设计、引信结构设计、防御工事的材料选择和结构设计都具有重要意义。