一种鸟体本构模型参数的反演方法
王卫伟
(中航西飞民用飞机有限责任公司 工程技术中心,西安 710089)
0 引言
随着仿真分析方法的成熟,使得在抗鸟撞结构设计中,仿真分析方法日益受到重视。通过鸟撞仿真分析可以指导对机体结构进行抗鸟撞优化设计。相对鸟撞试验,仿真分析可以大幅节省研制费用,缩短研制周期[1]。利用鸟撞仿真分析和鸟撞试验相结合的方法,能够节省试验的次数,降低试验的风险,并可以控制结构的质量及强度,最终完成结构选型设计[2-3]。仿真分析结果可靠与否,主要取决于鸟体本构模型中的参数是否准确,而鸟体形体及组成成分复杂,建立准确的鸟体模型难度较大,所以一般是把鸟体模型做简化处理。鸟体的参数可采用传统的人工试凑法或反演的方法,后者则更为可靠、省时[4]。目前,关于鸟体参数的反演方法,已有很多学者对鸟体参数的反演进行了研究,这些研究有的是基于神经网络方法进行鸟体参数反演,有的是借助非线性最小二乘法和外点罚函数法进行鸟体参数反演,有的是基于DOE参数筛选的方法进行鸟体参数反演[5-6],本文利用ISIGHT与PAM-CRASH集成进行优化反演,通过简化的鸟撞平板试验得到试验结果,将试验结果带入鸟体本构方程中,通过优化分析对鸟体本构模型的参数进行反演,可以得到可靠的鸟体本构模型参数。得到的参数可以用于复杂结构的鸟撞仿真分析。为利用商用软件进行鸟体参数反演提供了一种思路。
1 鸟体本构方程及参数合理范围
采用PAM-CRASH中的Monaghan状态方程作为鸟体本构方程。冲击波阵面上的Hugoniot压力可由下式确定:
式中,
γ=4k-1 (3)
其中:ρ0为鸟撞前鸟体的密度;ρ1为鸟撞过程中鸟体的密度;C0为零压力状态下材料内的声速;k为常数。
假设鸟体是基于空气和水的混合物,鸟体的B值和γ值范围则介于空气和水之间。空气和水的ρ0、C0和k值见表1。将表1中的数据代入(2)式和(3)式可得水的B= 3.14×108Pa,γ= 7.00;空气的B= 4.81×104Pa,γ= 3.12。据此,可确定鸟体B的取值范围为5.00×104Pa~3.00×108Pa,γ取值范围为3.00~7.00。

表1 水与空气的参数
2 鸟体本构模型参数反演方法
2.1 反演思想
确定了鸟体参数的范围之后,可以利用试验数据对鸟体参数进行优化。具体方法如下:(1)通过鸟撞平板试验得到位移随时间变化的曲线;(2)建立鸟撞平板试验耦合算法的数值计算模型;(3)将待优化反演的鸟体本构模型参数定义为优化参数,利用位移的试验值与计算值定义优化目标,再将计算模型整合到优化控制程序中,将参数初始值传递给计算模型,从而得到相应的计算结果;(4)将该结果与试验结果进行比对,若两者相差较大,则认为该组参数并不合理,优化控制器会自动产生一组新的参数,进行新一轮的计算,并如此反复的迭代,直到满足给定的误差要求,此时所得到的参数便是最优参数。
2.2 优化过程
参数的优化过程是利用ISIGHT和PAM-CRASH有机集成进行优化,优化流程图如图1所示。整个优化流程选用了2个Simcode组件,1个Calculator组件,1个Optimization组件。其中,Simcode-pamcrash组件用于读取输入文件,并对优化参数后的模型进行计算;Simcode-postprocess用于对计算后的结果文件进行处理,生成所需的撞击载荷随时间变化的曲线;Calculator组件用于对生成的结果曲线进行处理,输出目标函数的值;Optimization组件用于进行优化处理。

图1 优化流程图
在Optimization中,定义变量为GAMMA(即γ)的初始值为5,变量范围为3~7,变量B的初始值为1×107Pa,变量范围为5×104~3×108Pa。采用Hooke-Jeeves优化算法。
目标函数定义为仿真计算的平板位移与试验结果之间相对误差的平方,其表达式如下:
式中:Ds(i)为仿真计算得到的各个时间点下的位移值;De(i)为试验得到的各个时间点下的位移值;结果示于表2。根据(4)式可知,max(|Ds(i)|,|De(i)|)≠0,当Fer最小时,计算结果和实验结果的误差将达到最小。

表2 样本数据点的选取
2.3 优化结果
图2所示为优化变量与目标函数的迭代过程,图中横坐标为优化迭代的次数,纵坐标为相应的变量或误差值。由图2可以看到目标函数随着迭代过程的进行逐渐减小。经过迭代,可以得到优化结果,即当B为134000 kPa,且GAMMA为5.35时,误差达到最小0.1589。
3 鸟体参数反演结果的验证
采用优化后的鸟体参数进行鸟撞仿真分析,并与试验结果进行对比。
3.1 试验件与仿真模型建立
试验用试验件与夹具均为薄壁结构,试验件通过螺栓、压板连接到试验夹具上。装配好的试验件及支持结构如图3(a)所示,试验件支持结构的侧面细节如图3(b)所示。试验件规格、数量及所用材料见表3。

(a) B (b) GAMMA (c) Fer


表3 试验件规格、数量及所用材料
根据图3试验件及支持结构,仿真计算模型如图4所示,试验件与夹具均简化为壳单元,用Tied连接模拟螺栓,采用SPH方法对鸟弹模型进行处理[7-8]。
3.2 仿真结果与试验结果对比
将优化迭代后的仿真结果与真实的试验结果进行对比。
(1)位移对比:选取进行优化的平板中心点和R200mm某撞击点位移进行比对,如图5和图6所示。仿真计算的结果与试验结果的数值大小及曲线趋势皆具有很好的一致性。
(2)撞击力对比:撞击力对比见图7。在撞击载荷与试验测量真实值的对比上,虽然在峰值载荷上有一定的偏差,但两者之间的趋势具有很好的一致性。
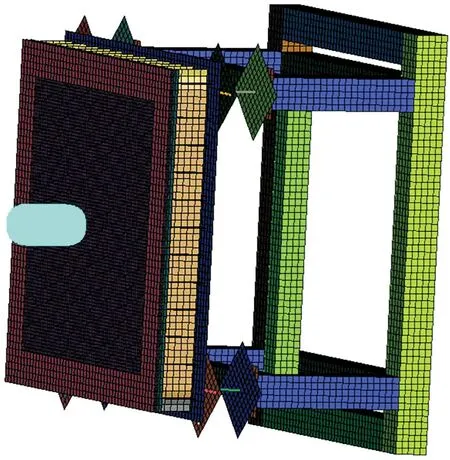
图4 仿真计算模型 图5平板中心点时间-位移曲线

4 结论
本文利用ISIGHT和PAM-CRASH有机集成对鸟体本构模型参数进行了优化。用优化后得到的鸟体本构模型参数进行仿真分析,并与试验结果进行对比。结果表明:两者位移大小及曲线趋势基本相同;仿真的撞击载荷与试验测量真实值虽然在峰值载荷上有一定的偏差;但两者之间的趋势具有很好的一致性。可见,鸟体本构模型参数的反演方法是合理的,得到的参数是可信的,对工程实际应用具有一定的借鉴意义。

