图说数学教育理论模型的建构

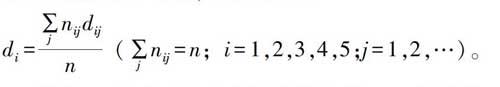
【摘 要】文章借助图形帮助教师直观地理解数学教育理论模型建构的常用方式，如MPCK理论的树形图模型、MKT理论的韦恩图模型、HPM理论的流程图模型、数学课程综合难度的雷达图模型、数学核心素养体系的几何体模型、数学核心素养评价的坐标系模型、数学教育双逻辑体系的对称图模型等。建构数学教育理论模型有助于教师形象且不失逻辑地诠释自己的教育教学观点和理论。

【关键词】图说;数学教育理论;模型建构

《数学写真集（第1季）——无需语言的证明》一书由许多“无需语言的证明”的图形组成，书中许多“证明”——图形令人拍案叫绝，充分显示了：“有什么比用插图来展现一个个重要的数学知识点更好的主意呢？”[1]笔者希望借助图形帮助广大教师直观地理解许多复杂、深奥的数学教育原理。

理论与实践本是相辅相成、辩证统一的关系，但很多中小学教师往往畏惧数学教育理论，认为理论过于抽象、难以理解。为此，笔者专门对30多个数学教育理论模型做了分析，发现数学教育理论模型的建构主要有树形图、韦恩图、流程图、雷达图、几何体、坐标系、对称图等形式，这些图形能形象且不失逻辑地向教师揭示某项理论研究的精髓。

一、MPCK理论的树形图模型

毋庸置疑，教师所具备的知识、能力、素养直接影响着教育质量。自20世纪80年代以来，人们从不同角度提出了许多关于教师的知识模型。其中，美国学者舒尔曼（Shulman）研究团队提出的Pedagogical Content Knowledge（简称PCK）理论，即学科教学知识或者教学内容知识理论有较大影响力[2-3]。

针对美国教师教育中的培养模式、教师资格认定和教师教育研究中所存在的学科知识与教育学知识脱节的现象，舒尔曼团队经过研究后提出PCK这一概念，认为成功的教学不仅需要教师的学科知识，而且需要教师的学科教学知识，也就是说为了促进学生的理解，教师必须自己先理解表征概念的方法，具备将教学内容转化为便于教学的知识。

PCK理论提出后，国外学者开展了大量的研究工作。2005年以后，PCK理论受到我国教育界的关注，并迅速成为教师知识研究领域的热门话题。

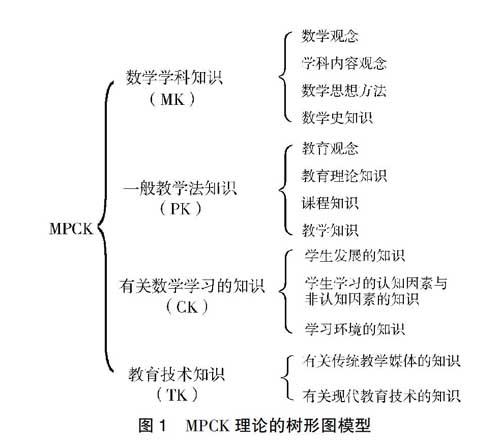
如果放在数学教学领域，讨论的就是数学教学内容知识，即Mathematical Pedagogical Content Knowledge（简称MPCK）。图1为MPCK理论的树形图模型[4]。该树形图模型的一个显著优点是把MPCK做了两级分类，便于人们开展局部与整体研究。其中，处在第一层级的四类知识分别是数学学科知识（MK）、一般教学法知识（PK）、有关数学学习的知识（CK）、教育技术知识（TK）。

与MPCK理论类似，我国的章建跃博士提出了“四个理解”的观点，他认为“理解数学、理解教学、理解学生、理解技术”（简称“四个理解”）是数学教师教好数学的前提，也是数学教学改革的基石[5]。虽然还没有人给出“四个理解”的理论模型，但“四个理解”的观点已经受到我国中学数学教师的青睐，截至2021年4月中国知网收录的以之为题的文章多达70余篇。

其实，无论MPCK还是“四个理解”，除了教育技术这个因素，两者还与数学教育学经典理论中的“三论”——数学课程论、数学教学论、数学学习论相吻合[6]。这就告诉我们，数学教育理论往往是相通的，它们是相同实质的不同表现形式。

利用树形图建构的理论模型还有数学教育学体系（曹才翰，1987）[7]、数学知识的分类模型（喻平，2000）[8]、高中数学研究型教学模式（李昌官，2018）[9]等。

二、MKT理论的韦恩图模型

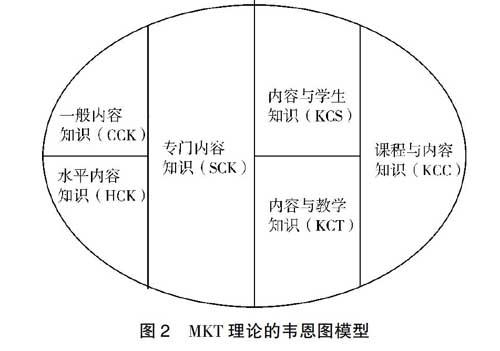
在上述MPCK理论的基础上，美国密歇根州立大学教育学院鲍尔（Ball）教授研究团隊于2000年前后提出了Mathematical Knowledge for Teaching（简称MKT）理论，即面向教学的数学知识理论。经过10年左右的不断完善，MKT理论的韦恩图模型如图2所示。

其中，一般内容知识（CCK）指除教学外，在其他背景下也使用的数学知识和技能;专门内容知识（SCK）指教学所特有的数学知识和技能;水平内容知识（HCK）指关于数学主题之间相互关联的知识;内容与学生知识（KCS）指把数学和学生学习情况相结合的知识;内容与教学知识（KCT）指把数学与教学相结合的知识;课程与内容知识（KCC）指关于课程标准、教科书等课程资源的知识。我们将CCK、SCK、HCK统称为学科内容知识（SMK），将KCS、KCT、KCC统称为教学内容知识（PCK）。

MKT理论将原来割裂的学科内容知识与教学内容知识融合并统一为面向教学的数学知识，并给出了精致的分类（即图2中的六个板块）。很多人认为MKT理论是“教好数学需要哪些类型的数学知识”这一问题当前最好的答案[10-11]。

与MKT理论相通的是我国的数学教学基本功经验。数学教学基本功是我国数学教研组师徒传承的宝贵经验，受到我国中学数学教师甚至教育主管部门的重视。数学教学基本功主要包括：（1）解题;（2）教材解读;（3）新授课教学设计;（4）课件制作;（5）课堂组织;（6）板书;（7）作业设计;（8）复习课与试卷讲评;（9）命题。它们可与MKT理论建立起对应关系。[12]

《普通高中数学课程标准（2017年版）》指出，数学教师应以《中学教师专业标准》为指导，提升自身的专业水平，数学教师要努力提升通识素养、数学专业素养、数学教育理论素养、教学实践能力，并对这四方面的素养或能力做了具体阐述[13]。这比MKT理论与数学教学基本功经验增加了教师的通识素养，具有更加宏观的指导意义。

利用韦恩图建构的理论模型还有数学竞赛（奥林匹克数学）的性质模型（罗增儒，2000）[14]、青年数学教师专业发展共同体ERTP理论模型（刘祖希等，2018）[15]等。

三、HPM理論的流程图模型

HPM是History and Pedagogy of Mathematics（数学史与数学教育）的简称。1972年，数学史与数学教学关系国际领导小组成立，标志着HPM作为一个研究领域正式出现。HPM自20世纪末引入我国，目前的研究达到了一个前所未有的高度，既有HPM的学术组织、研究团队、理论成果[16]，也有HPM的实践队伍、课例模式、案例成果[17-18]。华东师范大学汪晓勤教授研究团队建构的HPM理论如图3所示，这是一个流程图模型[19]。

这个模型展示了HPM理论的核心内容：立足1个视角（数学史），通过2座桥梁（历史与现实、数学与人文），采用4种形式（附加式、复制式、顺应式、重构式），遵循5个原则（科学性、可学性、有效性、人文性、趣味性），将数学史融入数学教学，发挥数学教学的6大价值（知识之谐、方法之美、探究之乐、能力之助、文化之魅、德育之效），实现立德树人的根本任务。这个HPM理论模型是中国学者对世界HPM的贡献，增强了中国数学教育研究的理论自信[20]。

利用流程图建构的理论模型还有关系—映射—反演（RMI）原理（徐利治，1983）[21]、数学建模的基本过程（《普通高中数学课程标准（2017年版）》）、数学主题教学设计的过程（《普通高中数学课程标准（2017年版）》）、数学“情境—问题”教学模式（吕传汉等，2001）[22]、基于数学文化的教学模式（张维忠等，2009）[23]、数学概念学习的APOS理论模型（杜宾斯基，1991）、数学教学设计原理（涂荣豹，2018）[24]、数学解题思维调节与控制系统（周春荔，2012）[25]、教育数学与数学教育的关系（张景中，1989）[26]等。

四、数学课程综合难度的雷达图模型

鲍建生教授于2002年在其博士学位论文中提出了数学课程综合难度的雷达图模型，如图4所示。该模型借鉴了美国国家教育统计中心工作报告（2001）中的课程总体难度（Overall difficulty）的概念，并结合数学学科的特征，以数学题的难度来衡量数学课程的难度[27-28]。数学课程综合难度的雷达图模型受到广泛引用，截至2021年4月中国知网收录的该模型引用文献高达390余篇。

这个模型包含五个难度因素：背景、探究、知识含量、推理、运算，每个因素又划分为不同的水平，根据等级权重，利用公式计算一组题目在每个因素上的加权平均数，具体如下：

di=∑jnijdijn（∑jnij=n;i=1，2，3，4，5;j=1，2，…）。

其中di表示五个难度因素的取值，dij表示第i个难度因素的第j个水平的权重，nij表示一组题目中属于第i个难度因素的第j个水平的题目的个数，其总和等于该组题目的总数n。

得到五个di值后就可以画出反映课程综合难度的五边形雷达图，根据图形的整体态势还可以分析课程的综合水平与难度特征。

当然，这个模型也有值得商榷的地方：一是以习题的难度代替课程（教科书）的难度，显然不够全面;二是习题的五个难度因素的划分既比较粗略，也没有对所获得的五个数值进行必要的整合。之后许多研究者对此进行了改进。[29]

利用雷达图建构的理论模型还有数学教材例题难度模型（濮安山等，2016）[30]、几何课程难度模型（史宁中等，2005）[31]、高中生数学学科核心素养测评框架（朱立明，2020）[32-33]等。

五、数学核心素养体系的几何体模型

自从《普通高中数学课程标准（2017年版）》提出了数学核心素养六要素：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析，许多研究者尝试建构数学核心素养体系的几何模型，比较典型的有三棱台模型（曹培英，如图5所示）[34]、魔方模型（孙成成、胡典顺）[35]、金字塔模型（吕世虎、吴振英）[36]。

笔者曾对这些模型分别进行了评析。其中，三棱台模型的优点是将《义务教育数学课程标准（2011年版）》提出的10个核心词（除去非数学特征的“创新意识”，并增加具有数学特征的“抽象”）归类到三棱台的6个顶点，上底面顶点表示的核心素养整体作用于下底面顶点表示的核心素养。该三棱台模型既做好了义务教育与普通高中数学课程标准的衔接，又突出了数学核心素养的层次[37]。

利用几何体建构的理论模型还有数学“四基”教学理论的正方体模型（张奠宙等，2011）[38]、数学学习力结构的圆锥模型（唐恒钧等，2016）[39]、HPM教学实践探究的三棱锥模型（王科，2017）[40]等。

六、数学核心素养评价的坐标系模型

《普通高中数学课程标准（2017年版）》指出，数学学业质量水平是六个数学学科核心素养水平的综合表现，每一个数学学科核心素养划分为三个水平，每一个水平通过数学学科核心素养在四个方面（情境与问题、知识与技能、思维与表达、交流与反思）的具体表现进行表述。这就是说，可以通过数学学科核心素养水平来评价学生的数学学业质量水平。据此，可从素养成分、素养体现、素养水平三个维度建构高中数学核心素养评价的坐标系模型，如图6所示[41]。

在这个模型中，每个点P（x，y，z）代表了某种数学核心素养（x=1，2，3，4，5，6）在某个方面（y=1，2，3，4）的表现为某一水平（z=1，2，3）。

利用坐标系建构的理论模型还有最近发展区理论的数轴模型（维果茨基，1932）、数学解题坐标系（罗增儒，1997）[42]、数学学习理论的研究框架（鲍建生等，2009）[43]、数学学科核心素养的结构（宁锐等，2019）[44]、数学教研论文写作的基本规律（刘祖希等，2016）[45]、数学文化的三维坐标系统（顾亚龙，2014）[46]等。

七、数学教育双逻辑体系的对称图模型

人們对完善的数学教育学体系孜孜以求。南京师范大学研究团队建构了数学教育双逻辑体系的理论模型，如图7所示，这是一个对称图模型[47]。该模型诠释了数学教育作为学科不但要遵循教与学的对应原则，还应该遵循教与数学对应的原则。也就是说，数学教育学体系需要双向建构，既要由一般教育理论演绎数学教育规律，也要由数学的学科特征提取数学教育规律。其中，教与学对应的中介因素包括教学论、课程论、学习论、教育技术，这些因素确保数学教学活动遵循教育教学的基本规律、遵循学生的心理特点;教与数学对应的中介因素包括教师的数学知识和经验、教育取向的数学哲学、教育数学、教育取向的数学史，这些因素直接影响数学教学活动的数学特征，即正确地、适当地体现数学的知识方法和思维价值。

数学教育双逻辑体系的理论模型可看作是对曹才翰教授在1987年提出的数学教育学体系的改进，其优化了原体系的逻辑和层次。

利用对称图建构的理论模型还有数学教育学研究的双逻辑起点（单墫、喻平，2001）[48]、数学教学中的思维活动（张乃达，1987）[49]、教师核心素养和能力双螺旋结构模型（王光明等，2019）[50]等。

综上所述，解读数学教育理论模型建构的常用方式，有助于教师理解理论与实践之间的联系，拓展理论的传播力和实践的生命力。期待广大数学教师选用合适的模型建构方式，诠释自己的教育教学理论和观点。

参考文献：

[1]NELSEN R B.数学写真集（第1季）：无需语言的证明[M].肖占魁，徐沙凤，译.北京：机械工业出版社，2014.

[2]SHULMAN L S.Those who understand：knowledge growth in teaching[J].Educational Research，1986（2）：4-14.

[3]SHULMAN L S.Knowledge and teaching：foundations of the new reform[J].Harvard Educational Review，1987（1）：1-22.

[4]李渺，宁连华.数学教学内容知识（MPCK）的构成成分表现形式及其意义[J].数学教育学报，2011（2）：10-14.

[5]章建跃.中学数学课改的十大论题[J].中学数学教学参考，2010（7）：2-5，11.

[6]新青年数学教师工作室.当代中国数学教育名言解读[M].上海：上海教育出版社，2015：24.

[7]曹才翰.论数学教育及其研究[J].数学通报，1987（9）：1-7.

[8]喻平.知识分类与数学教学[J].数学通报，2000（12）：12-14.

[9]李昌官.高中数学研究型教学实践与探索[J].课程·教材·教法，2018（1）：86-90，114.

[10]庞雅丽.美国MKT研究的缘起、发展及启示[J].外国中小学教育，2013（6）：36-40.

[11]黄友初.美国的教师教学知识研究：以MKT理论的发展为例[J].比较教育研究，2015（4）：83-89.

[12]任念兵，刘祖希.回归数学学科的教学基本功：兼谈“中学数学教师基本功”网络调查[J].中学数学杂志，2020（6）：1-4.

[13]中华人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2018.

[14]罗增儒.数学竞赛导论[M].西安：陕西师范大学出版社，2000.

[15]刘祖希，史嘉，陈飞，等.青年数学教师专业发展共同体的实践与思考：以“新青年数学教师工作室”为例[J].教育研究与评论（中学教育教学），2018（12）：22-29.

[16]汪晓勤.HPM：数学史与数学教育[M].北京：科学出版社，2017.

[17]汪晓勤，栗小妮.数学史与初中数学教学：理论、实践与案例[M].上海：华东师范大学出版社，2019.

[18]汪晓勤，沈中宇.数学史与高中数学教学：理论、实践与案例[M].上海：华东师范大学出版社，2020.

[19]纪妍琳，张佳淳，李怡泉.第七届HPM高级研修班综述[J].数学教学，2020（10）：22-27，43.

[20]刘祖希，陈飞.HPM与MM教育方式的耦合初探：兼谈当代中国数学教育流派[J].数学通报，2020（11）：31-34，49.

[21]徐利治.数学方法论选讲[M].武汉：华中工学院出版社，1983.

[22]吕传汉，汪秉彝.论中小学“数学情境与提出问题”的数学学习[J].数学教育学报，2001（4）：9-14.

[23]张维忠，徐晓芳.基于数学文化的教学模式构建[J].课程·教材·教法，2009（5）：47-50，70.

[24]涂荣豹.数学教学设计原理的构建[M].北京：科学出版社，2018.

[25]周春荔.数学思维概论[M].北京：北京师范大学出版社，2012.

[26]张景中.什么是“教育数学”[J].高等数学研究，2004（6）：2-6.

[27]鲍建生.中英两国初中数学课程综合难度的比较研究[D].上海：华东师范大学，2002.

[28]鲍建生.中英两国初中数学期望课程综合难度的比较[J].全球教育展望，2002（9）：48-52.

[29]吴立宝，曹一鸣.初中数学课程内容分布的国际比较研究[J].教育学报，2013（2）：29-36.

[30]濮安山，徐慧敏.PEP（A）版与IBID版数学教材中平面向量例题难度的比较[J].数学教育学报，2016（3）：10-13.

[31]史宁中，孔凡哲，李淑文.课程难度模型：我国义务教育几何课程难度的对比[J].东北师大学报（哲学社会科学版），2005（6）：151-155.

[32]朱立明.高中生数学学科核心素养测评指标体系的构建[J].教育科学，2020（4）：29-37.

[33]朱立明.高中生数学学科核心素养测评框架构建[J].中国教育学刊，2020（7）：78-83.

[34]曹培英.小学数学课程核心词演变的回顾、反思与展望[J].小学数学教师，2015（11）：4-9，57.

[35]孙成成，胡典顺.数学核心素养：历程、模型及发展路径[J].教育探索，2016（12）：27-30.

[36]吕世虎，吴振英.数学核心素养的内涵及其体系构建[J].课程·教材·教法，2017（9）：12-17.

[37]刘祖希.图说数学核心素养[J].中小学课堂教学研究，2020（10）：59-62.

[38]张奠宙，郑振初.“四基”数学模块教学的构建：兼谈数学思想方法的教学[J].数学教育学报，2011（5）：16-19.

[39]唐恒钧，陈碧芬，张维忠.基于学习力视角的高中数学课程建设[J].当代教育与文化，2016（2）：17-21.

[40]王科.HPM教学实践探究之三棱锥模型[M]//王瑞霖，王立东，黄兴丰.求索与追梦：中国青年数学教育研究者文萃.北京：北京师范大学出版社，2017.

[41]于川，朱小岩，邬楠，等.高中生数学学科核心素养水平调查及分析[J].数学教育学报，2018（2）：59-64.

[42]罗增儒.数学解题学引论[M].西安：陕西师范大学出版社，1997：182.

[43]鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009.

[44]宁锐，李昌勇，罗宗绪.数学学科核心素养的结构及其教学意义[J].数学教育学报，2019（2）：24-29.

[45]刘祖希，罗建宇.兴趣驱动 能力支撑 方法引领：浅谈中学数学教研论文写作的基本规律[J].中学数学杂志，2016（7）：16-19.

[46]顾亚龙.以文“化”人：小学数学文化的育人视界[M].上海：上海教育出版社，2014：16.

[47]徐伯华，涂荣豹.谈谈数学课堂的学科缺失[J].教学与管理，2011（4）：46-49.

[48]單墫，喻平.对我国数学教育学研究的反思[J].数学教育学报，2001（4）：4-8.

[49]张乃达.充分暴露数学思维过程是数学教学的指导原则[J].数学通报，1987（3）：6-11.

[50]王光明，黄蔚，吴立宝，等.教师核心素养和能力双螺旋结构模型[J].课程·教材·教法，2019（9）：132-138.

（责任编辑：陆顺演）