区间阻抗下无人驾驶接驳出租车合乘路径优化

刘津洋

(长沙理工大学 交通运输工程学院， 湖南 长沙 410114)

实际交通网络中行程时间包含很多不确定性。基于不确定条件对交通网络的路径优化研究主要分为两类：一是基于概率分布的期望时间，研究路径的行程时间概率分布；二是基于区间数据表达，用区间数据表示路网中的种种不确定性因素。现实生活中难以获取较精确的数据，而通过概率分布选取的最佳路径与数学模型的期望值成相关关系，但不能称之为最可靠路径。可见，更适合采用区间数据表达路网的不确定性。

2020年是中国无人驾驶车辆落地试运营的开局之年，全国各地多城市陆续开展了试运营相关测试。现阶段无人驾驶出租车不可随意切换路径，乘客必须在指定位置上下车。该文将多辆无人驾驶接驳出租车和合乘问题相结合，建立基于区间阻抗的最短路径优化模型。

1 问题描述

区间阻抗下无人驾驶接驳出租车合乘路径优化是以原始最短路模型为基础，考虑路网间阻抗的不确定因素，结合决策者的区间分析方法，形成对应约束条件，建立在区间阻抗数据背景下的最短路优化模型。模型可运用于出行者的路径方案选择决策，根据所求结果选择最佳出行路径方案。将路网详细描述成有向网络图G=(V，A)，其中V表示路网图中所有节点集合，A表示路网图中所有边的集合。起点、终点r,t∈V，(i,j)∈A表示路网内任意一条边，赋予边的区间阻抗为[lij,uij]，共有n辆车，每辆车的最大载客为Q人。路网中每个需求点有对应的上车需求人数，同时规定车辆行驶最大时间Tmax，目标是满足所有上车需求点且在规定时间内调度方案的鲁棒成本最小。

在区间阻抗背景下，两两区间值因为种种不确定因素不能进行直接比较，应考虑鲁棒偏差，即考虑出行者所选路径与当前情景下最短路的差值。某种情景用s表示，鲁棒偏差是在某种情景下与之相对应的网络整体状态。如从起点r到终点t的路径方案p，其鲁棒偏差为：

鲁棒偏差的大小可反映出行者选择该路径的后悔程度。因此，可根据所有情景下的鲁棒偏差，找到鲁棒偏差的最大值，再根据鲁棒优化的极小化极大值准则寻找鲁棒偏差的最小值路径即鲁棒最短路径。这里的路径鲁棒性是在当前情景选定路径与最坏情景最短路径之间的差值，出行者作出决策选择鲁棒最短路方案后，即使在所有不确定因素全部发生的条件下，也可保证当前的鲁棒最短路方案与实际最短路径差值最小。对交通枢纽接驳车辆、特殊工种车辆、灾区应急物流等有硬时间窗约束或对时间可靠性要求高的路径方案进行决策时，路径鲁棒性可作为关键评价指标。

2 模型构建

基于以上分析，构建鲁棒最短路混合整数规划模型。定义Xij、Wij为所选路网路径决策变量，当边(i,j)在鲁棒最短路径上时，Xij、Wij取1,否则取零。定义Y为车辆c所选路径决策变量，经过点i时取1，否则取零。以pickupi表示点i的乘车人数，passnodes表示上车需求点集合(这里讨论的情况为需求点全部满足)。边(i,j)的路径行程时间Cij可表示为lbij+(ubij-lbij)Xij(lbij为路段ij的下界值；ubij为路段ij的上界值)。xt表示当前情形下起点s到终点t的最短路径时间，是一个随变量Xijc取值而定的变量。混合整数规划模型如下：

(1)

约束条件如下：

xj≤xi+lij+(ubij-lb)Xij;∀(i,j)∈E

(2)

(3)

(4)

c∈1,…,n

(5)

(6)

Xijc+Xjic≤1,∀i,j∈E,c∈1,…,n

(7)

c∈1,…,n

(8)

(9)

c∈1,…,n

(10)

(11)

(12)

式中：E为路网中所有i、j点的集合。

式(1)中xt可描述为：

Xijc)]Wijc

(13)

对于Wijc，有：

(14)

式(1)为目标函数模型，表示求最小鲁棒成本下最优路径；式(2)为当前情景下最短路径约束；式(3)、式(4)为参照传统最短路径的所有选择路径的起点、终点约束；式(5)为路网各节点流量约束；式(6)表示上车需求点(必经节点)需全部满足；式(7)为避免两点间出现路径成环现象的约束；式(8)为各车辆行驶最大时间约束；式(9)表示每一个上车需求点(必经节点)只能被一辆车服务；式(10)表示上车需求点(必经节点)被车辆c服务，与经过当前节点的车辆c为同一辆；式(11)为车辆c的最大载客量约束；式(12)为其余变量取值范围。

3 算法设计

Benders分解算法在解决较大规模混合整数规划、随机规划等问题方面应用广泛。运用割平面的思想，将复杂变量固定后不断迭代求解产生新的约束，产生新的约束后主问题的约束增加产生新解，通过不断迭代计算求得最优解。该文研究的鲁棒成本，首先固定车辆路径，再计算在该情形下的最短路径，与Benders分解算法有异曲同工之处。因此，采用Benders分解算法对最小鲁棒成本下最优路径模型进行求解。步骤如下：

(2) 将路网中车辆经过的所有路径取区间阻抗的上界值，未经过路径取区间阻抗的下界值，求解子模型，获得新的最优解Wijc、Yic。如果目标函数值小于上界UB值，则更新UB。

(3) 将Wijc代入主模型，形成式(15)所示新的约束条件，得到新的解Xijc、Yic。如目标值z大于下界LB值，则更新LB。

lbij(1-Xijc)]Wijc

(15)

(4) 若UB=LB，目标模型得到最优解，停止计算。否则，进入下一步。

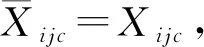
4 算例分析

采用图1所示交通仿真网络，对上述模型和算法进行论证。该路网由26个节点、61条路段组成，两点之间的区间阻抗值均作标记。在AMPL中编写Benders算法，写出对应主问题、子问题，并调用Gurobi求解器进行求解。

图1 路网测试图

车辆数设定为3台；需求点设置为7个,分别为路网中节点4、6、9、15、19、22、23，各点上车需求人数见表1；最大载客量设定为4，最大行驶时间设定为15 min。表1为车辆所满足的各个需求点，因设定最大载客量为4，需求点需求量的不同会对路径产生不同约束。

表1 上车需求点分配

3辆车鲁棒最短路径见表2，总鲁棒成本为26.7，路径形成见图2。

表2 鲁棒最短路径

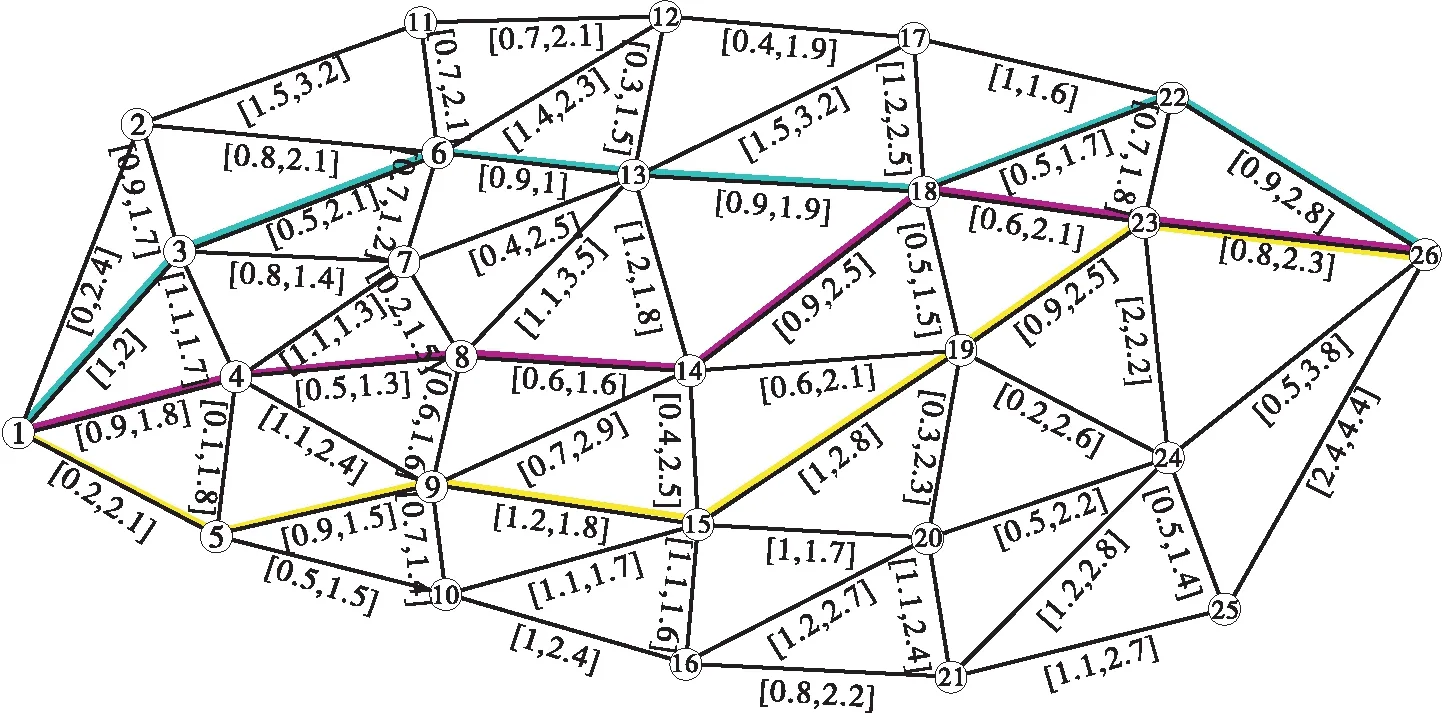
图2 鲁棒优化路径

表3为传统下界最短路的车辆行驶路径方案。虽然在3台车的行程时间区间中，下界值均比表2中鲁棒最短路径的下界时间小，但总体鲁棒成本大于表2中成本。鲁棒成本越大，则行程时间的不稳定性增加。说明所建立的基于区间阻抗的最短路径优化模型和算法可行，所得最短路径相较于传统最短路径具有更强的鲁棒性。

表3 下界最短路径

5 结语

结合无人驾驶路径研究热点，将多辆无人驾驶接驳出租车和合乘问题相结合，以总体鲁棒为目标成本，在满足乘客需求下，将车辆资源、环境资源、时间资源等做到最大整合，最大限度满足乘客需求和出行时间的稳定性要求。考虑到出行者在路网中选择出行路径方案时间的不确定性，建立基于区间阻抗的最短路径优化模型，模型经由CPLEX搭建并验证，验证过程中为避免非线性因素采用对偶模型,并设计Benders算法通过固定复杂变量进行求解。算例验证结果表明该鲁棒最短路径相较于传统最短路径具有更强的鲁棒性和稳定性，对于接驳运输、应急物流等均具有应用价值。