切比雪夫多项式的极性在定积分计算中的应用

赵云云,王勇强

(1.湖州市第一中学,浙江 湖州 313000；2.湖州市教育科学研究中心,浙江 湖州 313000)

0 引 言

积分的思想最早源于公元前200多年，希腊数学家阿基米德用积分的思想求出了球的体积公式.17世纪，开普勒、牛顿、莱布尼兹等著名数学家共同创立了初步的积分学.19世纪后，以柯西、威尔斯特拉斯等为代表的数学家对积分理论进行了深入探究，使积分学有了更坚实的极限理论基础.积分的出现不仅影响了数学的发展，还在很大程度上推动了物理、化学、生物、天文、工程、经济等学科的发展，积分的应用也越来越广泛.为拓展中学生的知识面，提高他们的数学应用能力，高中《数学》的选修内容(2-2)引入积分学知识，介绍了定积分的概念和经典计算公式——牛顿-莱布尼兹公式[1].

但在实际计算中，常有学生反馈以下情形不能用牛顿-莱布尼兹公式计算定积分：①仅仅利用普通的方法很难求得被积函数的原函数；②被积函数的原函数不是简单常见的初等函数；③被积函数没有适当的数学表示形式，其函数关系是通过图表的形式给出的.因此，作为教学补充，建立有效的数值方法来计算定积分是非常必要的.

关于切比雪夫多项式和数值积分方法的相关研究已较深入和广泛.文献[2]给出了切比雪夫多项式的定义、性质及相关应用；肖筱南利用插值多项式构造了各类插值型求积公式及其截断误差和代数精度[3]；吕书龙等研究了与切比雪夫多项式类似的Legendre多项式，以及Legendre多项式n个零点的计算和求积系数的求解，使得Gauss型求积公式能够更加简便地应用，也使利用Legendre-Gauss型公式计算所得的积分值与真实值的误差得到了很好的控制[4]；肖蒙等介绍了切比雪夫多项式的定义和性质及其在多项式插值中算法的实现[5]；向莹将切比雪夫多项式及第二类切比雪夫多项式的零点垂直映射到了单位圆周上[6]；杨平霞等介绍了一类复合插值型求积公式的构造方法[7]；王伟等研究阶数不变的插值型求积公式的代数精度可以取到的值，并给出了选取对应求积节点的具体方法[8]；徐晓芳等基于切比雪夫正交多项式零点插值误差的极小化性质,提出了非线性方程求根的一种新方法[9].但目前鲜少见文献探讨切比雪夫多项式的极性与数值积分方法的有效结合.本文主要研究切比雪夫多项式的性质在数值积分中的应用，探讨如何利用切比雪夫多项式的极性建立数值积分公式，使误差达到极小化.

符号说明：文中Ln表示以[a,b]上的n+1个等距节点为插值节点计算所得的积分值；In表示以[a,b]上的n+1个切比雪夫多项式的零点为插值节点计算所得的积分值；A(f(x))表示被积函数f(x)在[a,b]上积分所得的精确值；E(Ln)表示以[a,b]上的n+1个等距节点为插值节点计算所得的积分值与精确值的误差绝对值；E(In)表示以[a,b]上的n+1个切比雪夫多项式的零点为插值节点计算所得的积分值与精确值的误差绝对值;QNI表示采用普通插值型求积公式求解积分时，以切比雪夫多项式的零点为插值节点的积分方法；CQNI表示采用复化求积公式求解积分时，以切比雪夫多项式的零点为插值节点的积分方法.

1 预备知识

定义1[2]称多项式

Tn(x)=cos(narccosx)(-1≤x≤1,n=0,1,2,…)

为n次的切比雪夫多项式(第一类).

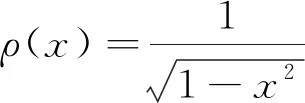
性质2(递推关系)[2]相邻的三个切比雪夫多项式具有三项递推关系式：

性质3[2]Tn(x)在区间[-1,1]上有n个不同的零点：

显然，Tn(x)在其中的零点都是实的、互异的，且全部在[-1,1]内.

性质4[2]Tn(x)在区间[-1,1]上有n+1个不同的极值点:

定义2[3]假设区间[a,b]上的n+1个节点为：

(1)

称为插值型求积公式.

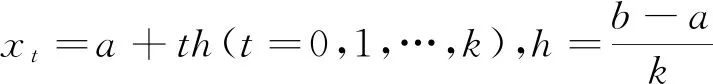
若在每个小区间[xt-1,xt]上应用式(1)，则

(2)

称为复化求积公式.

2 切比雪夫多项式的极性与数值求积

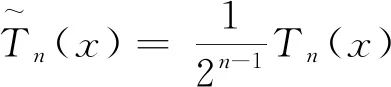
定理1称为切比雪夫多项式的极性，这种极性也是切比雪夫多项式的重要性质.

下面借助切比雪夫多项式的极性建立可使偏差极小化的数值求积公式.

定理2[3]设x0,x1,…,xn是区间[-1,1]上的n+1个互异节点，函数f(x)在[-1,1]上具有n+1阶连续导数f(n+1)(x)，在对f(x)用插值型求积公式(1)求积分时，截断误差的表达式为:

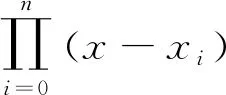
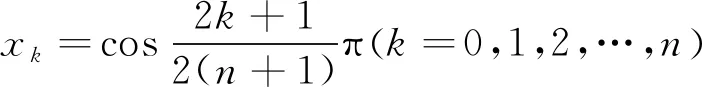
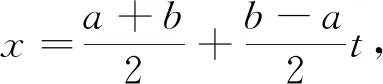
3 数值算法与数值实验

根据第二节的研究结果，建立如下求积算法：

(a)输入定义在区间[a,b]上的函数f(x)；

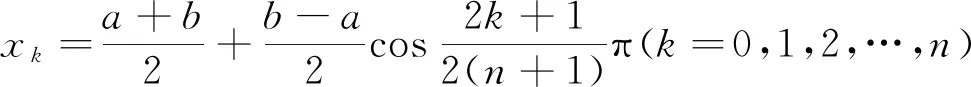
(c)将n+1个切比雪夫多项式的零点作为函数f(x)的插值节点，利用求积公式(1)或复化求积公式(2)求解,得出f(x)在区间[a,b]上的积分值.

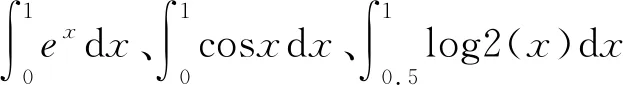
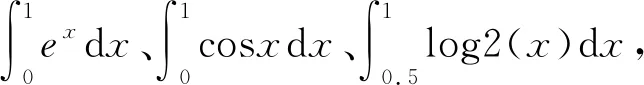
表1 QNI法和等距节点插值型积分公式的精度比较f(x)=ex、A(ex)=e-1

表2 QNI法和等距节点插值型积分公式的精度比较f(x)=cos(x)、A(cosx)=sin(1)

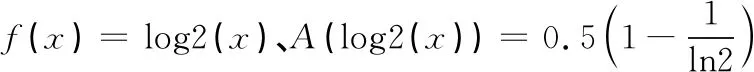
表3 QNI法和等距节点插值型积分公式的精度比较

例2利用复化求积公式，分别用CQNI法和等距节点插值型积分公式比较例1中3个积分值的精度.

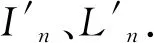
表4 CQNI法和复化等距节点插值积分公式的精度比较f(x)=ex、A(ex)=e-1

表5 CQNI法和复化等距节点插值积分公式的精度比较f(x)=cos(x)、A(cosx)=sin(1)

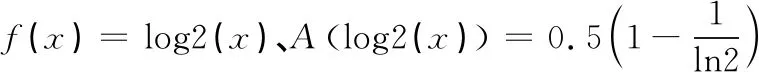
表6 CQNI法和复化等距节点插值积分公式的精度比较

综合例1和例2可知，无论是用插值求积公式还是复化求积公式，用QNI法或CQNI法计算所得的结果都更为精确，且利用复化求积公式求出的结果比插值型求积公式效果更好.

4 结 论

本文应用切比雪夫多项式的极性，将切比雪夫多项式的零点作为拉格朗日插值多项式的插值节点，将相应的拉格朗日插值多项式Ln(x)作为f(x)的近似函数，推导出插值型求积公式.该算法可使插值型求积公式的截断误差达到最小，并在此基础上得到复化求积公式.数值算例也证明了所建算法的有效性和优越性.