CPSO优化的非线性PI控制器在互联电网AGC中的应用

张轩豪 ，范 杨 ，鲍玉龙 2，李长辉 ，张 霆

（1.国网湖北省电力有限公司检修公司，湖北 武汉 430050；2.国网湖北省电力有限公司随州供电公司，湖北 随州 441300）

0 引言

光伏和风力等间歇式能源发电接入电网，对电网的二次频率调整带来了难以避免的的冲击［1-5］。电网调度中心通过自动发电控制（automatic generation control，AGC）对发电机组施加影响来应对幅度较大周期较长的负荷波动［6-13］。AGC控制器的结构和控制参数对电网频率调整的动态性能具有至关重要的作用。

现有的AGC控制器中，比例-积分（Proportional-Integral，PI）控制器基于其结构简单，性能优良等特点仍然占据着主流地位［14］。但是传统PI控制器，在复杂电力系统中参数整定困难，难以平衡AGC系统中控制精度和控制速度之间的矛盾［15］。很多学者结合使用范围对PI控制器结构进行了不同程度的改进。文献［16］提出了一种带有微分算子的模糊PI控制器，对于多区域电力系统的负荷扰动起到快速调节的作用。文献［17］将分数阶PID控制方法用于AGC控制中，显示了控制器非线性能力适应性强的优点，但是控制器设计较为复杂。在非线性PI控制的研究方面，文献［18］提出了非线性PI控制器并将其用于电力系统相位跟踪，提升了锁相环的相位跟踪速度。文献［19］验证了非线性PI控制器在开关电源中具有缩短过度过程的特点。系统的动态响应与PI控制器参数的整定精度也密切相关。粒子群算法由于其计算效率高，易于实现的特点，在处理低维问题上具有明显优势，但容易停滞在局部次优值处［20-22］。文献［23］详细分析了粒子群算法及其在电力系统中的应用。文献［24］将遗传算法与粒子群算法结合解决了非线性、大规模特点的变电站选址问题。文献［25］采用符号函数与惯性权重相乘以改变后期种群的搜索方向，但对收敛的粒子作用效果并不显著。文献［26］提出了混沌粒子群算法，对粒子进行二进制编码，通过二进制数组成的极大无关组的秩确定粒子进化方向，此算法计算量大，程序编写复杂。

本文设计了非线性PI控制器，并采用新型混沌粒子群算法对控制器参数进行优化，利用混沌理论的遍历性，优化了传统粒子群算法容易陷入局部最优的问题。

1互联电力系统AGC模型

1.1 模型描述

本文选用文献［14］仿真模型进行研究，选取包含控制器，调速器，汽轮机，发电机负荷等元件的等效传递函数替代实际系统。双区域电力系统结构如图1所示，各参数表示含义如表1所示。

图1 双区域互联电力系统AGC模型Fig.1 AGC system model of two-area interconnected power system

表1 互联电网参数及含义Table 1 Interconnected power system parameters and implications

调速器模型：

汽轮机模型：

发电机-负荷模型：

联络线功率交换模型：

1.2 目标函数设计

现行的AGC控制模式一般采用联络线功率偏差控制模式（Tie-Line Bias Control，TBC），当系统发生负荷波动时，由AGC控制器及时对区域控制偏差进行调节，维持区域电力系统频率稳定。单区域控制误差为：

1.3 非线性PI控制器设计

传统的PI控制器的比例控制基于控制偏差进行调节，比例增益参数一经确定无法更改，在控制过程中难以平衡扰动抑制和跟踪给定值两方面矛盾［12］。针对该问题，本文在传统PI控制器前加入非线性函数以改变PI控制器的比例增益，设计的非线性PI控制器的结构如图2所示。

图2 非线性PI控制器结构框图Fig.2 Nonlinear PI controller structure block

传统的PI控制器控制形式可以表示为：

非线性函数的设计本着与控制偏差同比例的原则，前期控制偏差较大时，kp应取较大值，加快调节速度，当控制偏差逐渐减小时，kp应逐渐减小，保证控制系统的稳定性。为此，本文选择如下形式的非线性增益函数：

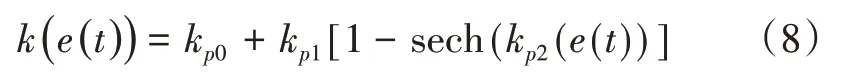
式（8）中，e（t）为系统误差，kp0，kp1，kp2为正系数，在调节过程中kp的值由（kp0+kp1）变化到kp0，kp2用于控制kp的衰减速度。

2 混沌粒子群算法

2.1 基本粒子群算法

粒子群算法将每个粒子的位置抽象成搜索空间的解，通过粒子间的信息传递，不断更新粒子的运动状态，逐渐获得最优解［27-30］。在D维搜索空间中的优化问题可以描述为：

F(x)表示粒子的适应度函数，用以对解的优劣作出判别。用Xi=[xi1，xi2，…，xid]和Vi=[vi1，vi2，…，vid]分别表示第i个粒子的位置和速度，所有粒子通过追踪个体极值Pbest和全局最优值Gbest来更新自己的位置和速度，粒子更新公式如式（10）和式（11）所示。

式（10）、式（11）中，k代表迭代次数，ω为惯性权重因子，r1，r2为［0，1］之间的随机数，c1，c2为加速系数。

2.2 混沌优化策略

混沌状态是指由一个确定性方程得到随机遍布于某一特定区域内的运动状态，呈现混沌状态的变量称为混沌变量，常见的混沌映射方程为：

式（12）中，μ为控制变量，zn为初始值，由式（12）可以看出，只要给定一个［0，1］之间的初始值，通过数次混沌迭代就能得到一组随机数据。这组数据具有两个方面的特点：随机性，即该数据杂乱无章，如同随机变量一般；遍历性，即它可以不重复的历经解空间中的所有状态。

粒子群算法虽然收敛速度快，却一旦陷入局部最优值附近，难以跳出局部最优解。若采取某种手段让其进入局部最优后能再次跳出来继续寻找最优解，则其陷入局部最优的概率会大大降低。本文采取这种思路，在判断种群聚集后，对全局最优值Gbest进行混沌搜索，并用混沌序列中的部分粒子替代部分早熟粒子，以此改善算法后期粒子多样性锐减的缺点。

综上所述，本文所提的改进混沌粒子群优化算法的流程如下：

步骤1 随机生成含有M个粒子的D维粒子群，并对粒子的速度和算法基本参数初始化；

步骤2 评价每个粒子的适应度值，保存Pbest和Gbest；

步骤3 判断是否达到终止条件，若是，则输出Gbest，否则，更新每个粒子的速度和位置；

步骤4 评价每个粒子的适应度值，若存在比Gbest更优的粒子，则将其位置设为Gbest，若存在比Pbest更优的粒子，则将其位置设为Pbest；

步骤5 判断粒子适应度方差，若σ2≥a，返回步骤3，否则对全局最优值Gbest执行混沌迭代：

2）按照Logistic混沌映射进行逐步迭代；

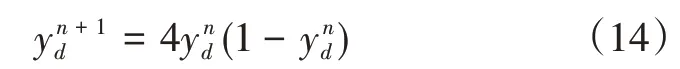
3）将混沌变量转换至解空间中；

4）计算新的解序列［x1，x2，…，xN］中所有解的适应度值，若优于初始解，则将新解作为结果。

步骤6 从新的解序列中挑选P个粒子替换原始解中P个非最优值粒子，转步骤3。

3 算例分析

在Matlab/Simulink中搭建电力系统仿真模型，采用所提算法调整PI控制器/非线性PI控制器参数。电力系统模型参数取值见表2，分别取传统粒子群算法和优化后的混沌优化粒子群算法进行对比分析，kp ki的取值范围设定在（0，10），粒子群规模取30个，迭代次数取100次。

表2 电力系统模型仿真参数Table 2 Simulation parameters of power system model

3.1 算法收敛分析

在初始时刻，给定区域一ΔPL1=0.05的阶跃负荷扰动，其算法迭代次数与目标函数值关系如图3所示。可以看出，标准粒子群算法迭代32次后，无法继续搜索得到更优解，而本文使用的新型混沌优化粒子群算法不仅在搜索精度上有所提升，在收敛速度上也有更好的效果。

图3 CPSO与PSO收敛曲线Fig.3 Convergence curves of CPSO and PSO

表3列出了两种算法的优化对照表，采用改进算法能得到更优的kp、ki参数，其ITAE值为0.001 6比基本粒子群的0.003 1减小了48.4%。将CPSO优化的参数应用到非线性PI控制器中，其ITAE值较CPSO优化的PI控制器下降了31.2%，较PSO优化的PI控制器下降了64.5%。

表3 PSO和CPSO优化结果对照表Table 3 Comparison table of PSO and CPSO optimization results

3.2 动态响应分析

建立如图（1）所示的双区域电力系统模型，在t=0时刻给区域一5%的阶跃负荷波动，观察系统的动态阶跃响应，系统的两区域动态响应如图4-图6所示，从图中可以看出，采用基于混沌粒子群优化的非线性PI控制器区域一频率偏差最大正超调为0.002 5 Hz，比CPSO优化的PI控制器的0.009 Hz降低了72.2%，比PSO优化的PI控制器的0.013 Hz降低了80.8%，能够使电力系统的频率波动和联络线功率波动尽快稳定在允许范围之内。

图4 区域一频率偏差Fig.4 Frequency deviation in area 1

图6 联络线功率波动Fig.6 Power fluctuation of tie-line

向模型中加入ΔPL1=0.05、ΔPL2=0.03的阶跃负荷扰动，系统阶跃响应对比图如图5所示，由图看出，采用本文算法优化的非线性PI控制器与CPSO优化的PI控制器和PSO优化的PI控制器相比，能更快地调整区域频率偏差和联络线功率波动。

图5 区域二频率偏差Fig.5 Frequency deviation in area 2

图7 区域一频率偏差Fig.7 Frequency deviation in area

图8 区域二频率偏差Fig.8 Frequency deviation in area 2

4结 论

本文对AGC机组PI控制器的结构和参数整定进行了研究，提出了一种基于混沌粒子群优化的非线性PI控制器，采用双区域电力系统模型仿真分析证明：

图9 联络线功率波动Fig.9 Power fluctuation of tie–line

1）将混沌优化理论引入传统粒子群算法中，利用混沌算法的遍历性，有效提升了传统粒子群的收敛速度和搜索精度，优化算法适应度值比传统算法减小了48.4%；

2）将变增益函数引入PI控制器后，能有效减小系统动态响应的超调量，加快响应速度，对于同样的阶跃扰动，非线性PI控制器的正超调量比PI控制器降低了72.2%；

3）将本文提出的基于CPSO优化的非线性PI控制器用于双区域电力系统的频率控制，可以有效降低系统频率偏差，减小联络线频率波动。