度量G-空间中的几类点集

冀占江，陈占和，张更容

(1.广西大学 数学与信息科学学院, 广西 南宁 530004;2.梧州学院 大数据与软件工程学院, 广西 梧州 543002;3.湖南第一师范学院 数学与计算科学学院, 长沙 410205)

0 引言

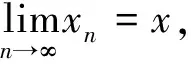
1 基本概念

定义1[9]设(X,d)是度量空间，G是拓扑群。称(X,G,φ)是度量G-空间，如果映射φ:G×X→X,满足:

① ∀x∈X,有φ(e,x)=x,其中e为G的单位元；

② ∀x∈X以及g1,g2∈G,有φ[g1,φ(g2,x)]=φ(g1g2,x)。

以下简称(X,G)是度量G-空间。为了书写方便，通常将φ(g,x)简写为gx。

备注若X是紧致度量空间，则称X是紧致度量G-空间。

定义2[9]设X,Y是度量G-空间，f:X→Y连续，若∀g∈G,∀x∈X,有f(gx)=gf(x),则称f是等价映射。

定义3[10]设X,Y是度量G-空间，f:X→Y连续，若∀g∈G,∀x∈X,∃h∈G使f(gx)=hf(x),则称f是伪等价映射。

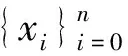
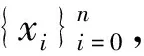
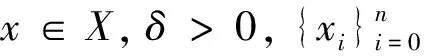
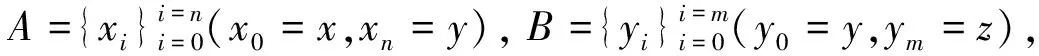
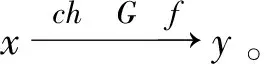
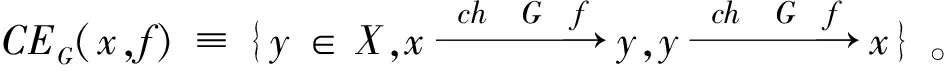
定义9[13]设(X,d)是度量G-空间，f:X→X连续，x∈X,称x是f的G-周期点，如果存在n∈N+,∃p∈G使得pfn(x)=x。f的G-周期点集用PG(f)表示。

定义10设(X,d)是度量G-空间，A⊂X,f:X→X连续，记GA≡{gx|g∈G,x∈X}。若G(A)⊂A,则称A对G不变。若G(A)=A,则称A对G强不变。

定义11设(X,d)是度量G-空间，f:X→X连续，x∈X,记

orbG(x,f)≡{gfm(x):g∈G,m∈N},

则称orbG(x,f)是x在f作用下的G-轨道。

2 相关引理

引理1[10]设(X,d)是紧致度量G-空间，G是紧致的拓扑群，则∀ε>0,∃0<δ<ε,∀g∈G,当d(x,y)<δ时，有d(gx,gy)<ε成立。

引理2[14]设(X,d)是紧致度量G-空间，G是紧致的拓扑群，f:X→X同胚伪等价，x∈X,则f(CEG(x,f))=CEG(x,f)。

引里3[15]设(X,d)是紧致度量G-空间，f:X→X等价，则CRG(f)是闭集。

引里4[12]设(X,d)是紧致度量G-空间，G是紧致可交换的拓扑群，f:X→X伪等价，n∈N+,则CRG(f)=CRG(fn)。

3 主要结果

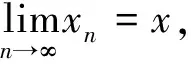
证明由引理1知，∀ε>0,∃0<ε0<ε,当d(z1,z2)<ε0时，∀g∈G,有

d(gz1,gz2)<ε。

(1)

由f的一致连续性知，对ε0>0,∃0<δ<ε0,当d(z3,z4)<δ时，有

d[f(z3),f(z4)]<ε0。

(2)

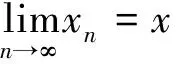
d(xm,x)<δ,

(3)

d[gmfkm(xm),a]<δ。

(4)

由式(2)知，

d[f(xm),f(x)]<ε0，

(5)

d[f(gmfkm(xm)),f(a)]<ε0。

(6)

由f伪等价知，∃tm∈G使

d[tmfkm+1(xm),f(a)]<ε0。

(7)

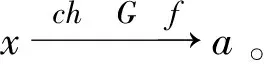
A∈CRG[fkm+1(xm),xm,ε,f],B∈CRG[f(x),x,ε,f]。

(8)

结合式(1)、式(7)知

(9)

令D={a,fkm+1(xm)}A{xm,f(x)}B,则D={a,fkm+1(xm)}A{xm,f(x)}B是f作用下的从a到x(G,ε)链，故a∈CEG(x,f)。

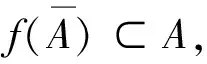
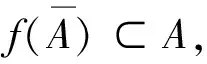
d(gx,gy)<ε。

(10)

反证法，若∃y∈CRG(f)-A使f(y)∈A。由引理4知，CRG(f)=CRG(f2),故y∈CRG(f2),则存在f2作用下(G,ε0)链{y0,y1,y2,…,yn-1,yn},其中y0=yn=y。因此对0≤i≤n-1,∃gi∈G,使

d[gif2(yi),yi+1]<ε0。

(11)

由式(10)知

(12)

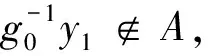
定理3设(X,d)是紧致度量G-空间，G是可交换拓扑群，f:X→X等价，则G(PG(f))=PG(f)。

证明显然PG(f)⊂G[PG(f)],下证G(PG(f))⊂PG(f)。设y∈PG(f),g∈G。由y∈PG(f)知，∃m∈N+,∃t∈G使tfm(y)=y。由f等价和G可交换知，fm(gy)=gfm(y)=gt-1y=t-1(gy),所以tfm(gy)=gy,则gy∈PG(f),因此G[PG(f)]⊂PG(f),故G[PG(f)]=PG(f)。

定理4设(X,d)是紧致度量G-空间，G是紧致拓扑群，f:X→X等度连续，则PG(f)是闭集。

(13)

由f等度连续性知，对ε0>0,∃0<δ<ε0,∀n≥0,当d(z3,z4)<δ时，有

d[fn(z3),fn(z4)]<ε0。

(14)

由y是PG(f)的聚点知，存在x∈PG(f)满足d(x,y)<δ。由x∈PG(f)知，∃m∈N+,∃t∈G使tfm(x)=x。结合d(x,y)<δ和式(13)、(14)知

(15)

因此,

d[tfm(y),y]

(16)

由ε的任意性知，tfm(y)=y,故y∈PG(f),则PG(f)是闭集。

4 总结

本文在拓扑群作用下度量空间中研究G-链等价集、G-链回归点集和G-周期点集的拓扑结构，得到一些新的结果，这些结果推广了度量空间中链等价集、链回归点集和周期点集的结论，为G-链等价集、G-链回归点集和G-周期点集在其他学科的应用提供了理论依据和科学基础。