导热系数对含空穴椭球形颗粒堆传热性能影响
刘泽砚,徐纪国,郑斌,王有镗,孙鹏,孟建,刘永启
(山东理工大学 交通与车辆工程学院,山东 淄博 255049)
0 引言
中国70 %以上的能源用于工业生产,其中至少有50 %转变为工业余热,余热回收效率仅有30 %[1-2],其余的余热以废热的形式排放至环境,能源利用率偏低。目前,在液体和气体余热回收方面的研究已经相对成熟[3-5],但是固体余热回收领域仍有很多问题亟待解决。据统计,我国每年可生成高温固体物料约50亿吨,若余热资源能全部被有效回收利用,可节省标准煤2.5亿吨以上,节能效果极为可观。目前常用两次换热法来回收固体余热,常见的有干熄焦和环冷机[6]。但此方法只适用于颗粒间隙大,气体容易通过的情况,同时对除尘系统要求高,增加了运营成本,普适性不高。针对密集堆积的高温颗粒,ZHENG等[7]提出一次换热余热回收法,即颗粒与换热器直接接触,通过一次换热实现余热的回收,此方法换热次数少、余热回收率高且广泛适应于各种高温固废,具有很强的适应性。在固体颗粒的堆积过程中,因为高温固体颗粒具有形状各异、粒径不均匀且表面粗糙、流动性差等特点,往往会在颗粒堆内部形成空穴,即颗粒缺失现象,这将对一次换热的余热回收效率带来不利影响。
针对固体颗粒余热回收过程,学者们已经进行了许多探索。卜昌盛等[8]研究了固定床内颗粒粒径、颗粒比热容、颗粒热导率等参数对固定床有效传热系数的影响。邹立臣等[9]研究了导热系数和比热容等煅后焦余热回收的影响。BU等[10]研究了颗粒间接触方式(面接触、短圆柱接触和间隙接触)对有序堆积床内流动换热的影响。顾永敏等[11]研究了陶瓷颗粒体系中传热系数的确定方法。赵强等[12]研究了煅后焦热物性对其余热回收的影响。针对空穴的热效应问题,张仲彬等[13]研究了带有空穴的相变胶囊后发现空穴使蓄热过程变得缓慢。田帅奇等[14]研究发现在低孔隙率下导热系数随空穴尺寸减小而增加。SOLOMON等[15]通过分子动力学技术发现热导率受空位浓度的影响。杨平等[16]研究了氮掺杂石墨烯纳米带的热导率,并通过非平衡分子动力学方法发现其热导率随空位而降低。LI等[17]从理论上研究了还有单空穴的石墨烯的热容、熵等热力学性质。
综上所述,目前的研究多集中于球形颗粒且未考虑空穴的存在,而含空穴的非球形颗粒堆与实际情况更为接近。同时,在基于一次换热的固体颗粒余热回收过程中,导热是主要传热途径[7],颗粒的导热系数是影响颗粒堆传热性能的核心参数之一,但对其详尽的影响规律的认知尚不系统。因此,本文以含空穴椭球形颗粒堆为研究对象,系统研究颗粒导热系数对颗粒堆传热性能的影响规律,以期为提升固体颗粒余热回收效率提供理论支持。
1 物理模型与数学描述
1.1 物理模型
颗粒堆内部空穴具有一定的复杂性,为更好地描述传热过程和提高计算精度,对物理模型做如下简化:①用表面光滑的椭圆形钢铁颗粒来模拟高温固体颗粒物;②仅考虑研究颗粒堆内部X和Y方向的传热,不考虑Z方向上的传热;③参考文献[10],选择简单立方堆积为颗粒的堆积方式,选择面接触为颗粒间接触方式,且选择面接触系数为0.05;④为避免换热壁面对空穴的影响,将空穴安置于颗粒堆中心。综上,所建立的物理模型如图1所示。颗粒为有序堆积且为规则的21行×21列,为简便叙述,用坐标形式(行号,列号)来代替颗粒位置,如(10,11)表示第10排11号颗粒。

图1 物理模型示意图
1.2 数学描述
颗粒堆无明显运动,与周围空气保持相对静止状态,参考岑可法等[18-19]研究,忽略颗粒堆内部对流换热,只考虑内部导热和辐射,数学描述如公式(1)至公式(4)。
(1)
式中,ρ表示密度,kg/m3;c表示比热容,J/(kg·K);T表示温度,K;t表示时间,s;λ表示导热系数,W/(m·K)。
(2)
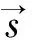
(3)
式中,εw表示表面发射率;T表示颗粒表面温度,K;qin表示入射到颗粒表面的辐射热流,W/m2。
(4)

1.3 初始条件和边界条件
物理模型的初始条件见表1。将模型的冷热壁面设置为定温壁面,将固固接触面、气固接触面均设置为耦合壁面,其余壁面设置为绝热壁面。
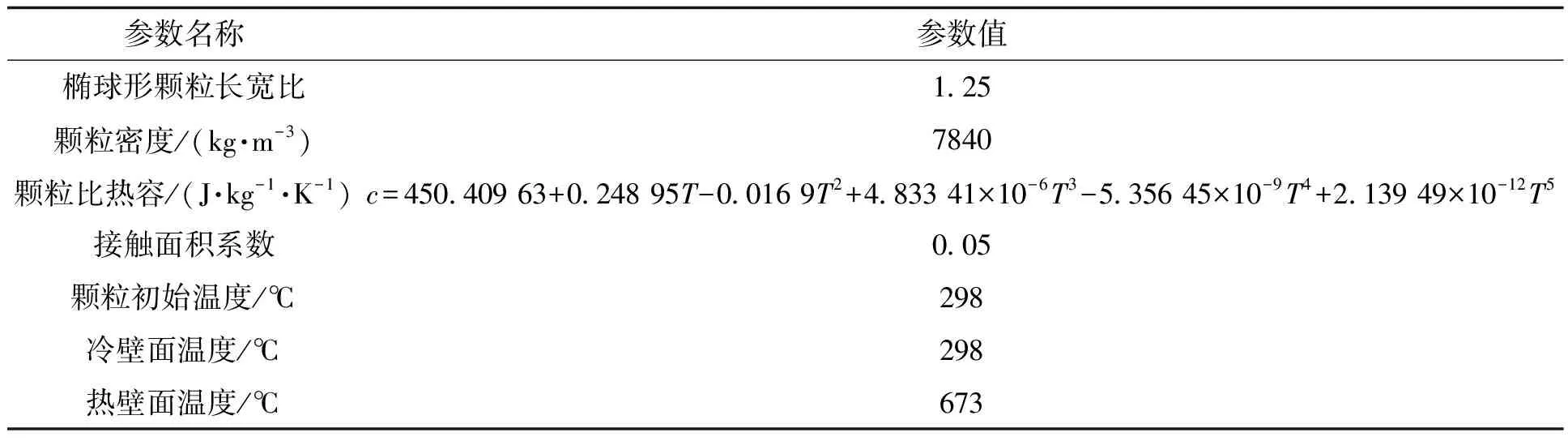
表1 初始条件
1.4 网格划分及独立性验证
本文使用间距为1 mm的网格对模型进行整体划分,并在空穴区域使用间距为0.5 mm的网格进行加密,如图2所示。

(a)整体网格
为保证计算精度且减少计算时间,对物理模型进行独立性验证。选取平均热流密度相对变化率为评价对象,以相对变化率小于1 %[20]为评价指标,结果见表2。

表2 网格独立性验证
方案3、方案4的平均热流密度相对变化率均小于1 %,在计算精度符合标准的前提下,方案3网格数目最少,可减少计算时间,因此选择方案3为最终网格划分方案。
1.5 主要研究对象及评价指标
本文选取颗粒长宽比(即椭球形颗粒长轴与短轴之比)为1.25的椭球形颗粒堆为研究对象,研究导热系数分别取0.5、1、5、10、50时颗粒堆内部的传热情况。选取温度、平均热流密度、表观热阻和空穴影响区域比为评价参数,对颗粒堆传热能力进行衡量。具体如下:
① 平均热流密度
随着导热系数的变化,平均热流密度必然变化,因此以平均热流密度来衡量颗粒堆的传热能力。计算公式如公式(5)至公式(6)。
(5)
(6)
式中,q为热流密度,kW/m2;Φ为颗粒堆总热通量,W;Ah为换热面积,m2;kh为平均热流密度相对变化率,%;qnv为无空穴颗粒堆平均热流密度,kW/m2;qv为有空穴颗粒堆平均热流密度,kW/m2。
② 表观热阻
空穴通过影响局部区域来影响传热,计算有一定难度,因此用表观热阻R从宏观角度来分析空穴对颗粒堆传热能力的阻碍效果。计算公式如公式(7)至公式(8)。
(7)
(8)
式中,R为表观热阻,K/W;ΔT为传热模型冷热壁面温度差值,K;kR为表观热阻相对变化率,%;Rnv为无空穴颗粒堆表观热阻,K/W;Rv为有空穴颗粒堆表观热阻,K/W。
③ 空穴影响区域比
导热系数不同,空穴对颗粒堆内部的影响程度不同,选用空穴影响区域比来衡量空穴对周围颗粒的影响能力。本文认为有无空穴颗粒堆对应颗粒温度之差大于冷热壁面差值的0.5 %(即1.875 K)为受影响区域。计算公式如公式(9)所示。
(9)
式中,Rv为空穴影响区域比,%;Av为受空穴影响区域的面积,m2;As为颗粒堆表面积,m2。
2 结果与分析
2.1 导热系数对含空穴椭球形颗粒堆温度的影响
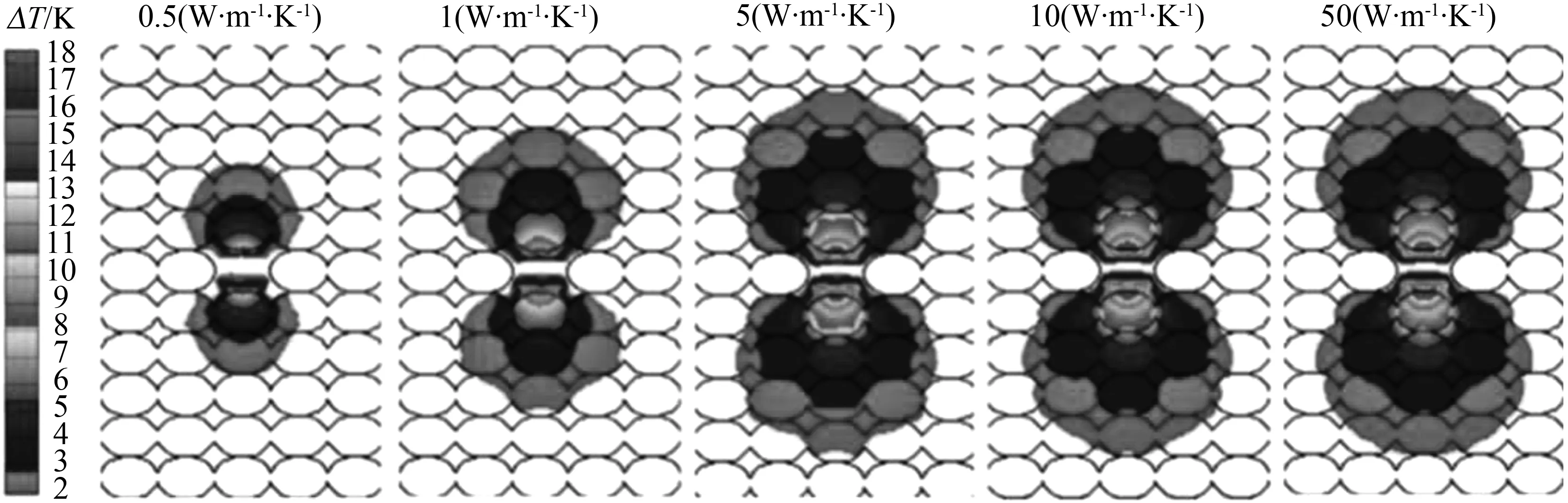
图3是导热系数变化对有空穴颗粒堆温度影响示意图。由图可知,颗粒堆内部存在空穴时会影响周围颗粒的温度,其中相邻两排颗粒受影响最明显。空穴上游颗粒温度降低,空穴下游颗粒温度升高。随着导热系数增大,温度在空穴区域的波动程度增大,且受影响排数增多。这是因为颗粒缺失之后,空穴区域被不容易导热的空气填充,热流传递路线受阻。空穴下方颗粒热量积聚,温度升高,与两侧颗粒形成温度差,热流流向两侧。而空穴上方的颗粒的很难从空穴处吸收热量,温度降低,所以第10排颗粒热流由两侧流向中间。正是因为热流的“旁路流”作用,使得空穴的影响向两侧扩散。
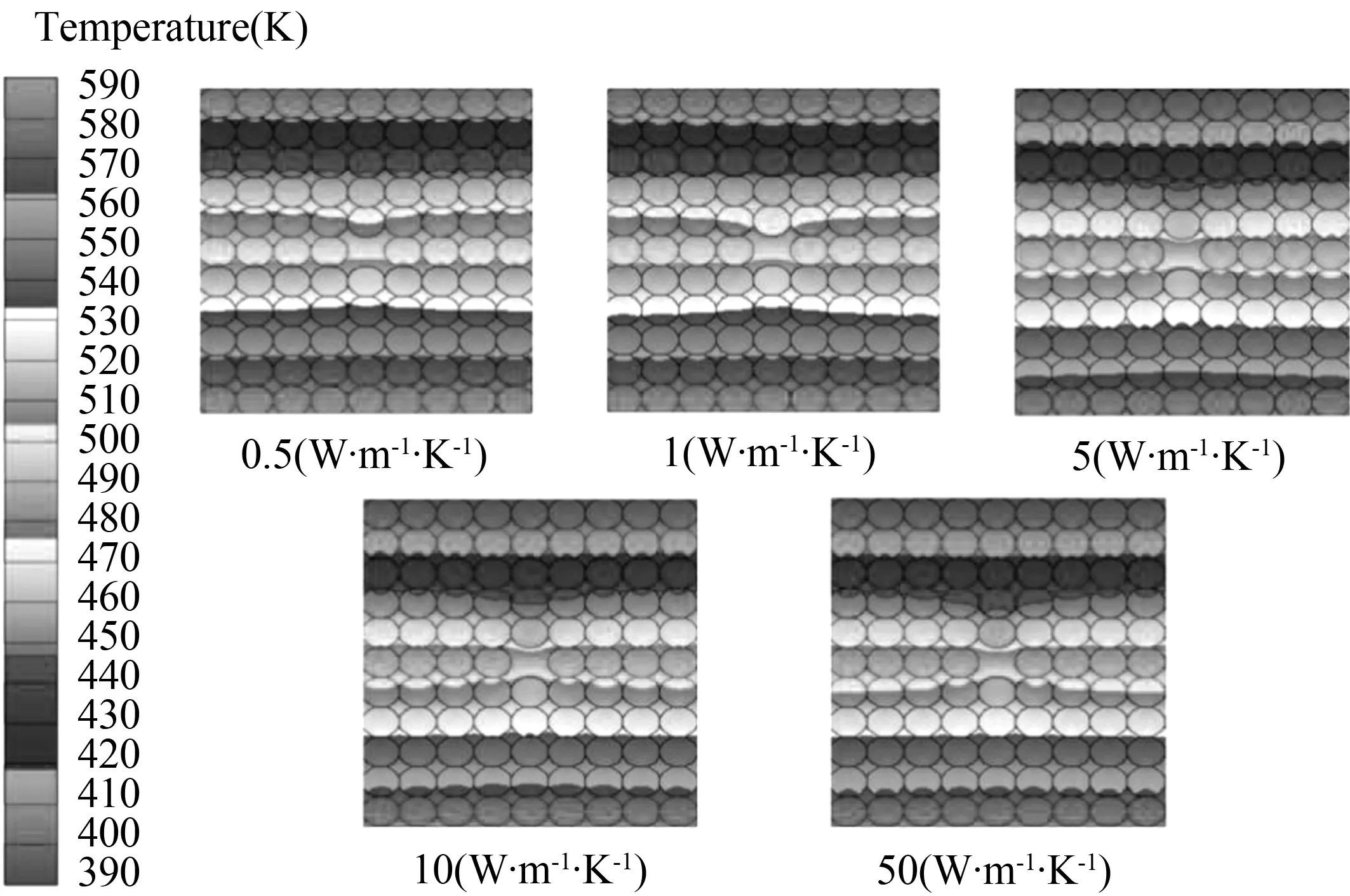
图3 导热系数变化对有空穴颗粒堆温度的影响云图
根据图3的分析可知,被空穴影响最明显的是相邻的第10排和第12排颗粒。因此,以第10排和第12排颗粒为主要研究对象来分析不同导热系数对有空穴颗粒堆的具体作用。图4为第10排颗粒温度变化图。由图4(a)可知,受空穴影响,不同导热系数颗粒堆第10排颗粒均呈现出温度由两侧向中间降低的规律。随导热系数增大,第10排颗粒的整体温度降低。图4(b)是有无空穴颗粒堆第10排颗粒温度变化最大值的变化。随着颗粒导热系数增加,第10排颗粒最大温差增大。导热系数由0.5 W/(m·K)增至50 W/(m·K)时,第10排颗粒最大温差由5.018 ℃增至10.378 ℃。这是因为空穴的“旁路流”作用,第(10,11)号颗粒得不到热量补充,热流由两侧颗粒流向11号颗粒,所以温度呈现由两侧向中间降低的规律。同时,颗粒导热系数越大,热流传递更快,相比与无空穴工况,有空穴颗粒堆第(10,11)号颗粒从空穴处得到的热量越少,所以第10排颗粒最大温差增大。
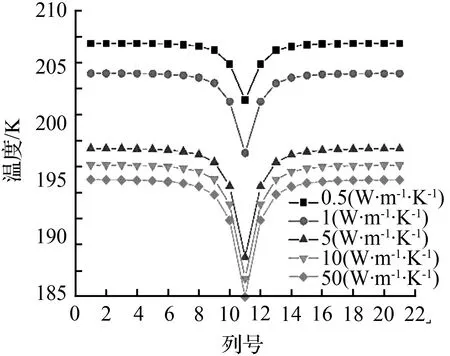
(a)第10排颗粒温度
图5是导热系数对有空穴颗粒堆第12排颗粒温度的影响。由图5(a)可知,受空穴影响,第12排颗粒均呈现出由中间向两侧降低的规律。随着导热系数增大,第12排颗粒温度整体降低。图5(b)是为第12排颗粒温度变化最大值。随着导热系数增大,最大温差增大,由277.849 K增至283.376 K。这是因为受空穴处“旁路流”的影响,第(12,11)号颗粒热量积聚,温度升高。热量由中间流向两侧,导致12排颗粒温度由中间向两侧降低。导热系数越大的颗粒堆在(12,11)号颗粒热量积聚的越多,所以12排颗粒最大温差增大。
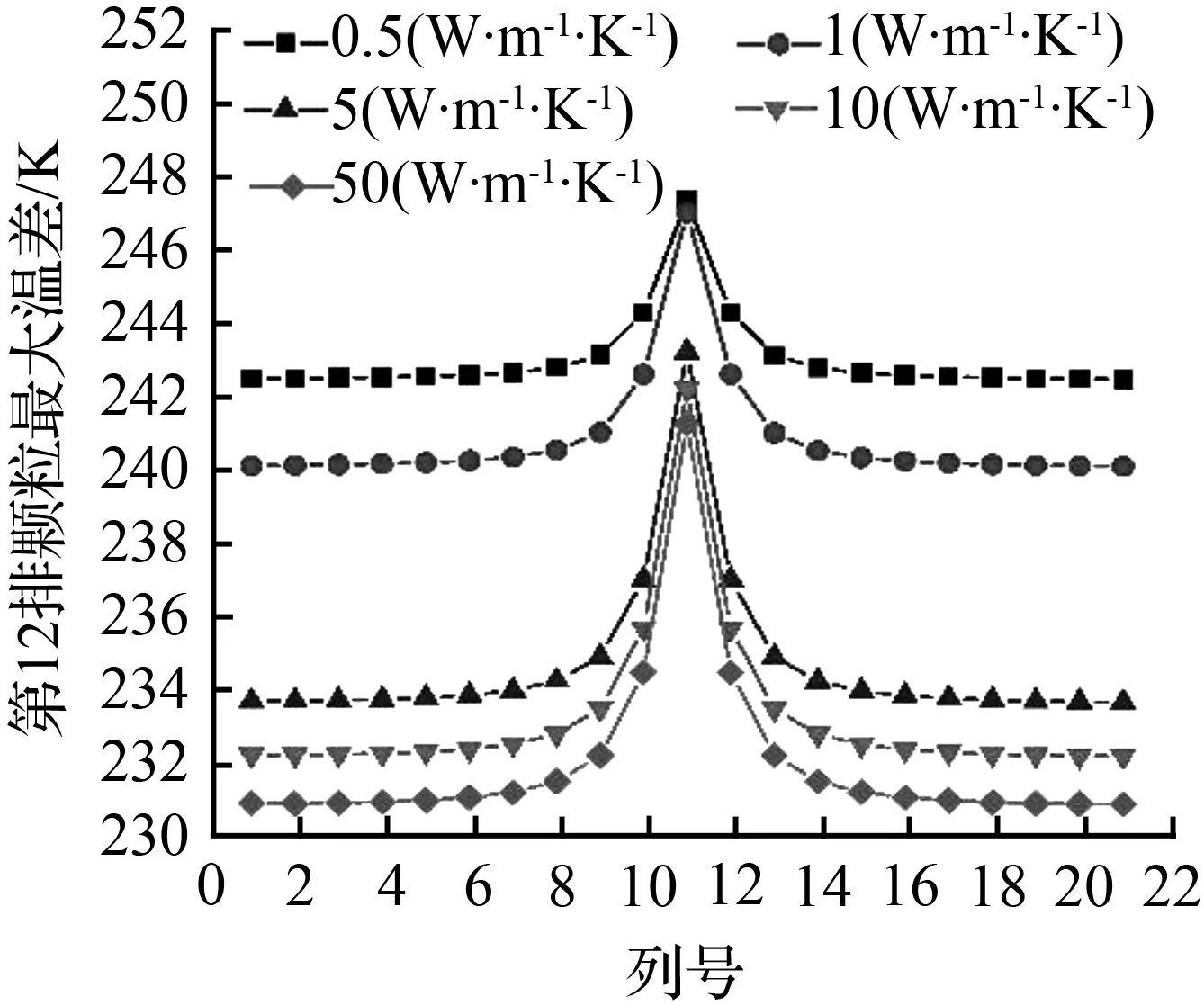
(a)第12排颗粒温度
2.2 导热系数对有无空穴椭球形颗粒堆热流和热阻的影响
图6为导热系数对有无空穴颗粒堆热流的影响。由图6(a)可知,随导热系数增加,两种工况平均热流密度均增加,且每一种导热系数下的无空穴工况的平均热流密度均大于有空穴工况。当导热系数由0.5 W/(m·K)增至50 W/(m·K)时,无空穴颗粒堆平均热流密度由0.447 kW/m2增至31.301 kW/m2,有空穴工况则由0.446 kW/m2增至30.097 kW/m2。图6(b)从平均热流密度的相对变化率分析,随导热系数增大,相对变化率增大,由0.312 %增至0.658 %。这是因为根据傅里叶定律,导热系数越大的颗粒堆热量传递越快,所以平均热流密度呈增加趋势。而空穴区域被比热容远大于颗粒的空气填充,热量存在损失,所以无空穴工况平均热流密度大于有空穴工况。同时,空气的导热系数极小,传热极为困难,这使得空穴对导热系数越大的颗粒堆影响越大。所以平均热流密度相对变化率随导热系数增加而增加。
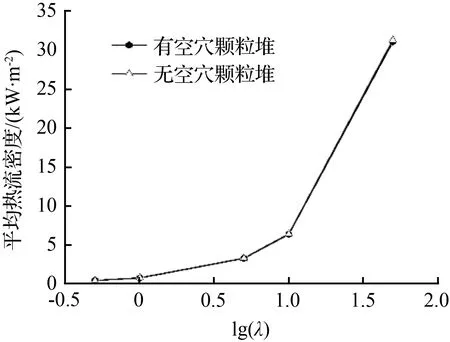
(a)平均热流密度
图7为导热系数对有无空穴颗粒堆表观热阻的影响。由图7(a)可知,随导热系数增大,表观热阻减小,且有空穴工况表观热阻均大于无空穴工况。当导热系数由0.5 W/(m·K)增至50 W/(m·K)时,有空穴颗粒堆表观热阻由766.117 K/W降至10.978 K/W,无空穴工况则由763.732 K/W增至10.907 K/W。这是因为在颗粒堆温度梯度相同的条件下,颗粒导热系数增大,热流传递更为迅速,所以表观热阻减小。而有空穴颗粒堆空穴区域被空气填充,导致局部区域热阻增大,因此相比于无空穴工况,有空穴颗粒堆表观热阻略大。图7(b)为表观热阻相对变化率,由图可知,随着颗粒导热系数增加,表观热阻相对变化率增加,由0.312 %增至0.658 %。这是因为随着颗粒导热系数增大,空穴区域和周围颗粒的传热更为困难,导致空穴的影响增大,所以相对与无空穴颗粒堆表观热阻变化率增大。
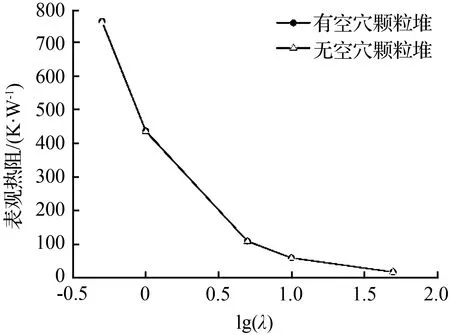
(a)表观热阻
2.3 导热系数对含空穴椭球形颗粒的影响区域比
图8为空穴对颗粒堆内部影响区域示意图。由图8(a)可知,空穴对上下游颗粒的影响区域分别成环形分布。随导热系数增加,被空穴影响的面积增大。受影响区域中与空穴相邻的两颗粒温度梯度最大。图8(b)为空穴影响区域比的变化,随导热系数由0.5 W/(m·K)增至50 W/(m·K),空穴影响区域比由1.599 %增至6.058 %。这是因为颗粒导热系数增大之后,空穴区域与周围颗粒导热系数梯度增大,导热更为困难,热量在第12排颗粒积聚增多,导致影响区域增大。
(a)影响区域云图
3 结论
针对固体颗粒余热回收过程中,颗粒堆内常出现空穴的现象,构建了含空穴的椭球形颗粒堆稳态换热模型,系统研究了颗粒导热系数对椭球形颗粒堆传热性能的影响规律。研究结果如下:
① 随着颗粒导热系数增加,空穴周围颗粒温度的波动程度增加。空穴对相邻两排颗粒影响最为明显,颗粒堆内第10排颗粒温度由两侧向中间降低,第12排颗粒温度由中间向两侧降低。随着导热系数增大,第10排和第12排颗粒温度变化最大值均增大。
② 随着颗粒导热系数增加,颗粒堆的平均热流密度增加,表观热阻减小,当颗粒导热系数由0.5 W/(m·K)增至50 W/(m·K),平均热流密度由0.446 kW/m2增至30.097 kW/m2,表观热阻由766.117 K/W降至10.978 K/W。随着导热系数增加,空穴对颗粒堆传热影响度增加,颗粒堆的平均热流密度相对变化率增加,表观热阻相对变化率增加,当颗粒导热系数由0.5 W/(m·K)增至50 W/(m·K),颗粒堆的平均热流密度相对变化率由0.312 %增至0.658 %,表观热阻相对变化率由0.312 %增至0.658 %。空穴对周围颗粒的影响区域呈环形分布,且随颗粒导热系数增加而增大,当颗粒导热系数由0.5W/(m·K)增至50 W/(m·K),空穴影响区域比由1.599 %增至6.058 %。

