基于格的无证书盲签名方案

张小萍

（广西大学计算机与电子信息学院,广西南宁530004）

基于身份的签名体制[1]是利用用户的身份信息作为公钥,不需要证书去认证,由私钥生成中心（KGC）来生成用户私钥,这样就大大简化了PKI对证书的管理,降低了密钥管理的开销.但是,由于KGC掌握了所有用户的私钥,所以存在着密钥托管问题,一旦KGC不可信或者系统主密钥泄露,所有用户的私钥都将变得不安全.无证书的公钥密码体制[2]的提出解决了密钥托管问题,在无证书的密码体制中,用户身份信息作为用户的部分公钥,KGC只生成用户的部分私钥,无法掌握用户的完整私钥,所以基于无证书的签名比基于身份的签名安全性更强,比传统基于证书的签名效率更高.

盲签名[3]是一种特殊签名,在签名人和消息拥有者的交互协议中,签名人在不知道具体消息内容的情况下对消息进行签名,签名人也无法将签名的中间过程和最终签名联系起来.由于盲签名具有保护消息拥有者隐私的性质,因此盲签名在电子选举、电子投票、电子现金中有许多重要的应用.

无证书的盲签名是将无证书的密码体制和盲签名相结合的签名方案,目前已有的无证书的盲签名方案[4-6]是基于整数分解和离散对数等数论假设难题提出的,在量子计算机下,基于数论假设难题被证明是可以在多项式时间内求解的[7],寻找能够抵抗量子攻击的公钥密码体制成为急需解决的问题.基于格构建的公钥密码体制具有抵抗量子攻击的优点,目前为止发现最快攻击格困难问题算法的时间复杂度还不存在亚指数级,达到了指数级,这为格密码体制在量子攻击的安全性提供了保障.在格基上构建无证书的签名已经获得了一些研究成果,以格困难问题构建了无证书的加密方案[8],无证书签名[9]和前向安全的签名方案[10]以及无证书代理重签名方案[11],但是还没有出现格上无证书的盲签名方案.

2012年,Lyubashevsky利用拒绝采样技术提出一个无陷门的格签名方案[12],拒绝采样算法的核心思想是使输出签名的分布与所使用的密钥分布相互独立,无法从签名分析出密钥的分布特征.相对于已有的抽样技术的签名方案,这个签名方案的效率比较高.本文在格上提出一个无证书的盲签名方案,方案使用文献[9]提出的矩阵采样算法来生成用户的部分私钥,以拒绝采样算法来生成签名.在格上最小整数解困难问题的假设下,提出方案满足随机语言模型下选择消息和选择身份攻击的不可伪造性.

1 预备知识

1.1 格上的相关定义

定义1格：令B=[b1,b2,...,bm]∈Rn×m是一组基,其中向量b1,b2,...,bm∈Rn并且线性无关,定义由一组基B生成的格Λ=L（B）={Bv|v∈Zn}.

定义2 q模格：对于q∈Z,u∈Z nq和A∈Z n×m,定义2种整数格Λ⊥（A）={e∈Zm：Ae=0 modq}和=Λ⊥u（A）{e∈Zm：Ae=umodq}.

定义3格上离散高斯分布：令s＞0,c∈Rn,Λ是一个格,则Λ上的高斯分布是其中ρs,c（x）=exp（-π‖x-c‖2/s2）.

定义4小整数解问题（SISq,n,m,β）：给定q∈Z和A∈Zn×m,β（n）是一个有界多项式函数,求解非零向量满足Ae=0 modq.

1.2 格上的相关技术

定理1格陷门生成技术[13]：给定n,q≥2,m≥（5+3θ）nlogq,θ是一个固定常数,存在一个概率多项式算法TrapGen（q,m,n）输出且满足：A在统计上接近于上的均匀分布,TA是Λ⊥（A）上的基,

定理3拒绝采样算法：若V是Zm的一个子集并且V中所有元素的范数都小于h：V→R是一个概率分布.若s←S表示从集合S中均匀随机选择一个元素s.

那么存在一个常数M=O（1）使算法A和算法F两者分布的统计距离不超过2-w(logm）/M.

2 无证书盲签名方案（CLBS）的定义与安全性要求

2.1 形式化定义

一个CLBS方案由下面4个多项式时间算法组成：

（1）系统初始化：输入安全参数n,输出系统主密钥makey和系统公开参数para.

（2）密钥提取：输入系统主密钥makey,系统公开参数para和签名人身份信息ID,生成签名人的部分私钥DID并发送给签名人,签名人选择一个秘密值SID,根据SID和DID,获得签名人的私钥skID和公钥pkID.

（3）盲签名生成：输入系统公开参数para,欲签名消息msg,签名人身份信息ID和私钥skID,签名人和用户之间进行一系列交互协议后输出签名sig.

（4）签名验证：输入系统公开参数para,签名人ID和公钥pkID以及消息签名对（msg,sig）,对签名进行验证,若签名验证成功则输出是,否则输出否.

2.2 安全性要求

（1）盲性：签名者在签名时无法获得签名的内容,事后也无法将最终签名和某个签名过程联系起来.

（2）不可伪造性：无证书盲签名方案定义了2种敌手AI和A∏,其中AI不知道系统主密钥,但能对签名人秘密值对应的部分公钥进行替换,用于模拟外部攻击者;A∏可以获得系统主密钥,但不能替换签名人公钥,用于模拟内部攻击者.如果方案能够抵抗这2种敌手的存在性伪造攻击,那么方案就具有不可伪造性.

3 格上CLBS签名方案

3.1 系统初始化

选择安全的参数n,q＞2是一个素数,b,λ是正整数,m1＞2nlogq,m2＞64+nlogq（/2b+1）,m=m1+m2,运行TrapGen（n,m,q）,输出一个校验矩阵和Λ⊥（A）的一组基.然后,KGC选择2个安全的哈希函数再选择一个随机矩阵公开参数para={A,B,H1,H2）,KGC的主私钥是TA.

3.2 密钥生成

用户（身份为ID）密钥的生成具体步骤如下：

①KGC运行采样算法SampleMa（tA,TA,s,H（1ID））,输出一个矩阵并发送给用户就是用户的部分私钥.

③用户计算PID=BSID,用户的完整私钥就是skID=（DID,SID）,完整公钥是pkID=（H1（ID）,PID）.

3.3 盲签名生成

假设要签名的消息是msg,签名人（身份为ID）和消息拥有者U之间的交互过程由以下步骤组成：

②盲化：U收到c′ 后随机选择3个向量计算发送给签名人.

④去盲：消息拥有者U计算,输出签名sig=（msg,ε,z,c）.

3.4 签名验证

任何验证人都可以通过下面的计算进行验证签名的正确性.

4 安全性分析

4.1 正确性

定理4提出的CLBS方案满足正确性.

证明

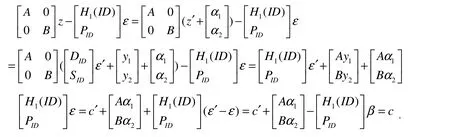
4.2 盲性

定理5提出的无证书盲签名满足盲性.

证明：假设（msg,ε,z,c）是任意一个有效的盲签名,是某次盲签名过程中签名人获得的视图,考查下面3个关系式

需要证明满足（1）（2）式的盲因子也满足（3）式.因为（msg,ε,z,c）是一个有效的盲签名,所以

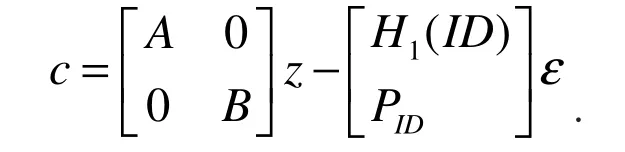
所以由（1）、（2）式求解出（α1,α2,β）满足（3）式,任意一个有效签名（msg,ε,z,c）和中间视图之间都可以确定唯一的一组盲因子而不产生矛盾,签名者无法将签名的中间视图和最终的某个有效签名对应起来.所以,提出的方案满足盲性.

4.3 不可伪造性

定理7在随机预言模型下,如果存在敌手AI能在多项式时间内,最多经过q1次H1询问,q2次H2询问,qb次部分密钥询问,qm次秘密值询问,qp次公钥询问,qt次公钥替换询问,qs次签名询问以不可忽略的概率θ伪造签名,那么就存在挑战者CH利用敌手AI可以在多项式时间内以概率θ2/（2qp（q2+qs））解决SISq,n,m,β问题.

证明：挑战者CH和敌手AI以下面的步骤进行游戏

（1）系统初始化：选择安全的参数n,q＞2是一个素数,b,λ是正整数,m1＞2nlogq,m2＞64+nlogq/（2b+1）,.随机选择2个矩阵,初始化3个表L1,L2和LS.

（2）AI可以对CH发起以下的询问：

H1询问：敌手AI发送IDi给挑战者CH,希望获得H1（IDi）,CH先查询表L1,若表L1中已有身份IDi,则将其对应的FID�发给AI;CH选择随机的,计算,将存入表L1,将FID�发送给AI.H2询问：敌手AI发送（c,msg）给挑战者CH,CH先查询表L2,若表L2中已有（c,msg）对应的哈希值,就直接发送给AI,否则,随机选择,将（c,msg,ε）存入表L2,将CH发送给AI.

部分私钥询问：敌手AI向挑战者CH发送IDi希望获得IDi的部分私钥,否则挑战者CH查询表L1,若已有身份IDi,则将其对应的发给AI,否则先进行H1询问,再返回给AI.

秘密值询问：敌手AI向挑战者CH发送IDi,希望获得IDi的秘密值,挑战者CH查询表L1,若L1中已有身份IDi,则将其对应的发给AI,否则先进行H1询问,再返回给AI.

公钥询问：敌手AI向挑战者CH发送IDi希望获得IDi的公钥,挑战者CH查询表L1,若L1已有身份IDi,则将其对应的公钥发给AI,否则先进行H1询问.

公钥替换询问：敌手AI向挑战者CH发送,若L1中已有身份IDi,则用替换掉原来的对应值将更新后的存回表L1.否则先进行H1询问,再进行更新.

签名询问：CH用表LS维护签名询问.当AI想获得（IDi,msg）的盲签名时,若在表LS中找到相应信息就返回给AI,如果找不到,就由CH按照第3章盲签名的生成过程生成签名（IDi,msg,ε,z,c）并保存到表LS并发给AI.

（3）伪造签名：敌手AI成功伪造出一个身份ID*的有效签名（msg*,ε*,z*,c*）.其中ID*没有进行过部分私钥询问,（ID*,msg*）没有进行过签名询问,敌手AI选择身份ID*伪造签名的概率是1/qp.在没有进行H2询问的情况下,敌手AI猜对ε*的概率是（1/3）k.

根据分叉引理[14],可以至少以概率生成身份ID*关于消息msg*的另一个有效签名（msg*,ε*,z*,c*）,那么满足

可以将z*和z′表示成以下形式

那么可以得到

所以挑战者CH在多项式时间内至少以概率（2q（pq2+q）s）解决SISq,n,m,β困难问题,其中

定理8在随机预言模型下,如果存在敌手A∏能在多项式时间内,最多经过q1次H1询问,q2次H2询问,qb次部分密钥询问,qm次秘密值询问,qp次公钥询问,qs次签名询问以不可忽略的概率θ伪造签名,那么就存在挑战者CH利用敌手A∏可以在多项式时间内以概率θ2/（2qp（q2+qs））解决SISq,n,m,β问题.

证明：和定理7的证明类似,敌手A∏和挑战者CH进行一些步骤的游戏,初始化阶段和定理7证明相同,在询问阶段敌手不能进行公钥替换询问,其他询问也和定理5证明相同.在伪造签名阶段敌手A∏成功伪造出一个身份ID*的有效签名（msg*,ε*,z*,c*）.其中ID*没有进行过秘密值询问（ID*,msg*）没有进行过签名询问,敌手选择身份ID*伪造签名的概率至少是1/qp.

可以将z*和z′表示成以下形式

那么可以得到

综合定理5和定理6的证明,提出的CLBS方案可以抵抗两种敌手AI和A∏的伪造攻击,所有具有不可伪造性.

5 结束语

量子计算机的发展使得传统的无证书盲签名方案变得不安全,基于格困难问题构建的签名体制具有抵抗量子攻击的优势,本文提出的格上无证书的盲签名方案利用格上SIS困难问题并使用了矩阵采样技术和无陷门的拒绝采样技术来构建签名,经证明提出的方案在随机预言模型下具有不可伪造性,并且可以抵抗量子算法攻击,具有更高的安全性,也丰富了格上关于无证书密码签名方案种类的具体构建.在本文提出方案的基础上,为了满足一些比较特殊的应用需求,构建格上无证书的部分盲签名方案和限制性部分盲签名方案将是下一步要研究的内容.