基于神经网络的数控机床丝杠热评价模型
徐祐民,陈秀梅,涂怡蓉
(北京信息科技大学 机电工程学院,北京 100192)
0 引言
作为数控机床的主要传动部件之一,滚珠丝杠在运行中与丝杠两端的轴承以及丝杠螺母发生摩擦,其温度不断升高并发生热变形。滚珠丝杠的热变形会严重影响到零件的加工精度[1-2]。有资料显示,由发热导致的误差占机床加工整体误差的40%~70%[3-6],因此通过热评价对数控机床状态进行评估是十分必要的。
随着人工智能技术的广泛应用,国内外学者将神经网络应用于滚珠丝杠发热问题的研究。辛宗霈等[7]针对机床进给系统热误差,使用BP神经网络提出了一种复合预测方法,该方法预测精度比直接法提高了126%;靳增锋等[8]利用神经网络模型对热误差进行建模,使最大预测误差降低到2 μm;Yang等[9]使用神经网络对电主轴的热误差进行预测,准确率可达86%。以上研究多集中于数控机床热误差的模型建立与预测,对数控机床的热评价研究较少。本文利用粒子群优化支持向量机神经网络(PSO-SVM)、分数阶粒子群优化BP神经网络(FPSO-BP)、普通BP神经网络3种神经网络建立滚珠丝杠的热评价模型,对数控机床进行热评价,为数控机床热评价体系研究提供方法。
1 模型建立
1.1 支持向量机
支持向量机(support vector machine,SVM)是由Vapnik等[10]提出的一种机器学习算法,其目的是在高维空间中设计一种分离特征平面的方法,该算法利用高维特征空间中的核函数,寻找支持向量及其相应的系数,构造一个最优的分离平面。
对于线性不可分的数据集,可以利用核函数将低维度的数据转化到高维度,使用平面进行分类。径向基核函数(RBF)为
K(x,xi)=exp(-γ‖x-xi‖2)γ>0
(1)
式中:xi(i=1,2,…,M)为数据集的特征向量;γ为拉格朗日乘子。此核函数中通过欧氏距离判断两个实例的相似性[11]。在RBF函数中,支持向量个数、权值和阈值均由支持向量机训练算法自动生成,具有良好的分类效果。
1.2 BP神经网络及优化
BP神经网络是由Rumerlhart等在20世纪80年代提出的一种逆向传输的多层神经网络,其基本结构如图1所示。

图1 神经网络结构
BP神经网络的鲁棒性好、容错能力强,在机器学习中得到广泛应用,但是它也存在算法收敛速度慢、过早收敛等缺点。本文在使用BP神经网络建立评价模型时,针对BP神经网络的缺点采用分数阶粒子群(FPSO)优化BP神经网络建立评价模型。
1.3 粒子群算法与分数阶粒子群算法
粒子群算法是一种类似于遗传算法的基于群体协作的随机搜索算法。假设D维空间中,有m个粒子组成初始种群,粒子在当前空间进行搜索时,Xi表示粒子在空间中的位置,Vi表示粒子在当前空间的速度,通过式(2)、(3)不断更新粒子的速度和位置,并且计算粒子的适应度值:
Vi(t+1)=Vi(t)+c1r1(pbesti-xi(t))+
c2r2(gbesti-xi(t))
(2)
xi(t+1)=xi(t)+Vi(t+1)
(3)
式中:Pbesti表示粒子的历史最优位置,gbesti表示粒子全局最优位置。当粒子群的寻优结果满足预先设置的要求或达到最大搜寻次数时,停止搜寻。本文利用PSO这种基于群体的智能算法,对SVM模型的惩罚因子C和核函数参数g进行寻优,以提高模型的分类精确度。
分数阶微分具有良好的鲁棒性、抗干扰性和记忆性。利用分数阶微分可将粒子群算法的速度公式更新为[12]:
c1r1(qij(t)-xij(t))+c2r2(qjk(t)-xij(t))
(4)
式中α为分数阶次。更新后的公式将1个参考项增加为3个,使得粒子个体和群体的速度和位置的更新变化更为准确,记忆信息更加丰富。
基于神经网络的数控机床滚珠丝杠热评价模型建立流程如图2所示。

图2 热评价模型建立流程
2 滚珠丝杠温度采集
为建立滚珠丝杠的温变预测模型,需要采集数控机床运行中滚珠丝杠的温度。由于在数控机床运行中,滚珠丝杠做旋转运动,因此要直接测量丝杠的温度变化数据比较困难。考虑到滚珠丝杠系统中左、右端轴承和丝杠螺母产生的热量大部分传递到丝杠中,虽有一定温差,但整体变化趋势相同,本实验采集滚珠丝杠两端轴承套和丝杠螺母上的温度数据并取平均值对模型进行验证。传感器贴装位置如图3所示。

图3 传感器贴装位置
设定使用1~5年的数控机床为“优”等级,使用6~10年的数控机床为“良”等级,使用11~15年的数控机床为“中”等级,使用16~20年的数控机床为“差”等级。以正常使用状况下同一类型、不同年限的16台数控机床为研究对象,每种等级选取4台,在滚珠丝杠空载、进给速度为3 000 r/min、润滑脂润滑、室温24 ℃条件下,分别采集这4种年限的机床滚珠丝杠系统的前轴承、后轴承和丝杠螺母套的温度。每种等级的每台数控机床采集60组数据,将滚珠丝杠两端以及丝杠螺母套上的数据取平均值作为滚珠丝杠的温度变化数据。
取得的初始数据较为杂乱,为保证训练后的模型精度,对数据进行预处理。本文使用最小二乘法对收集的数据做3次多项式拟合,设置最小二乘法拟合数据作为“过滤器”,取每组数据中误差小于等于0.1并且靠近拟合曲线的50个数据作为数据集。
3 仿真分析
以采集的数据建立数据集,对数据进行划分并处理。抽取每个等级的前40组作为训练样本,后10组作为测试样本。对数据进行归一化处理,消除特征之间差别导致的影响。构建滚珠丝杠热评价模型后,使用训练样本进行训练,使用测试样本进行仿真。
3.1 PSO-SVM热评价模型仿真
设定不同的PSO参数对热评价模型进行训练,经过多次实验,最终设定PSO基本参数,如表1所示。

表1 PSO基本参数设定
通过Matlab编写程序,利用设定好参数的PSO算法对SVM参数进行优化得到以下结果:最佳惩罚参数c=2.768 2,最佳核参数g=90.532 9,在CV意义下分类准确率为100%。粒子群适应度曲线如图4所示。
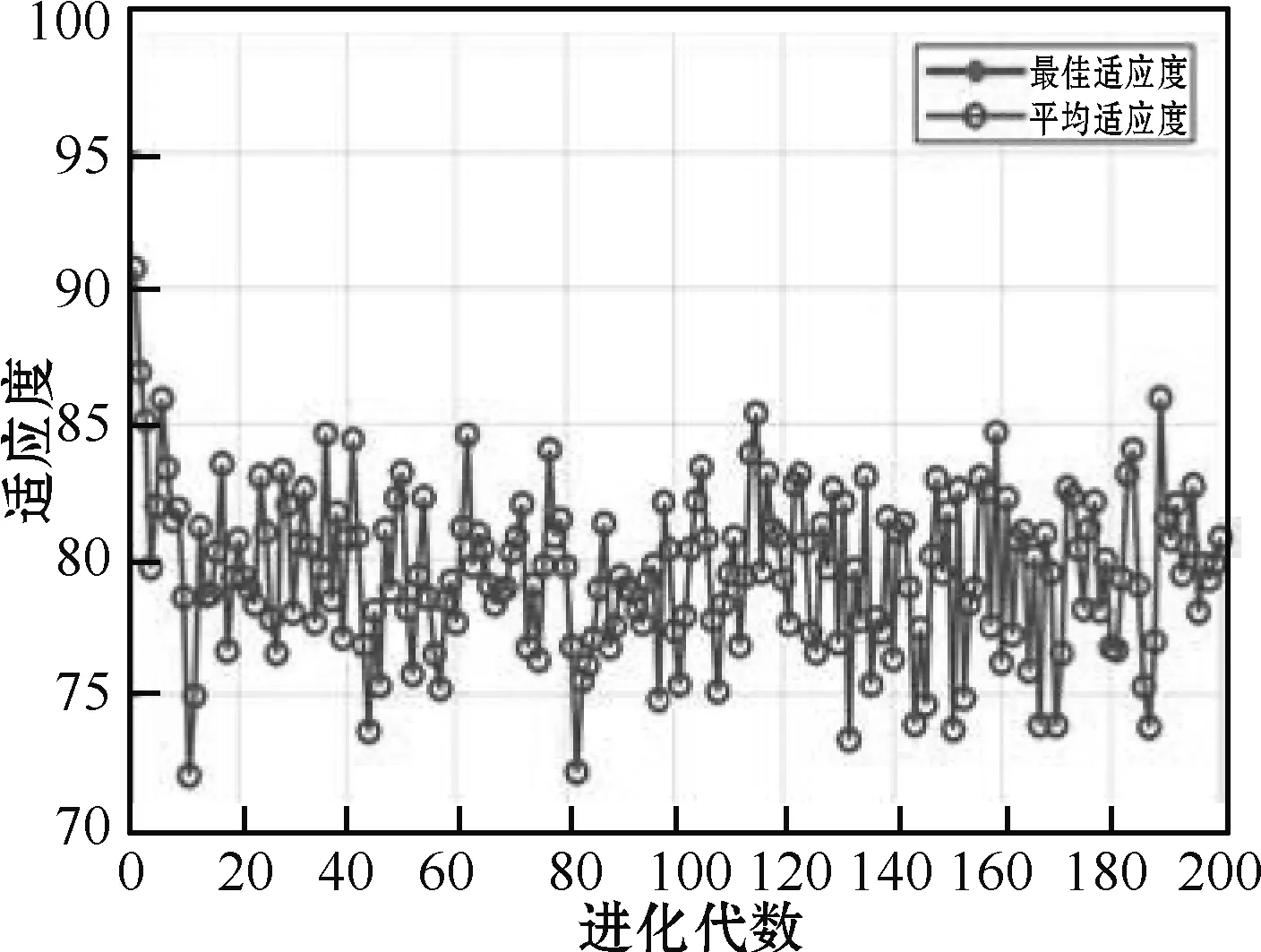
图4 粒子群(PSO)适应度曲线
使用最佳惩罚参数和最佳核参数对模型进行训练,利用处理后的数据进行仿真,得到测试集实际分类和预测分类如图5所示。在图5中,横坐标代表测试集数据序号,纵坐标代表机床滚珠丝杠分级,其中1~4依次为优、良、中、差等级滚珠丝杠。当代表预测测试数据的“*”与代表实际分类的“○”重合时,说明预测分类与实际分类相同。PSO-SVM滚珠丝杠热评价模型分类准确率为92.5%(37/40),在中等级滚珠丝杠分类中出现3处误差。
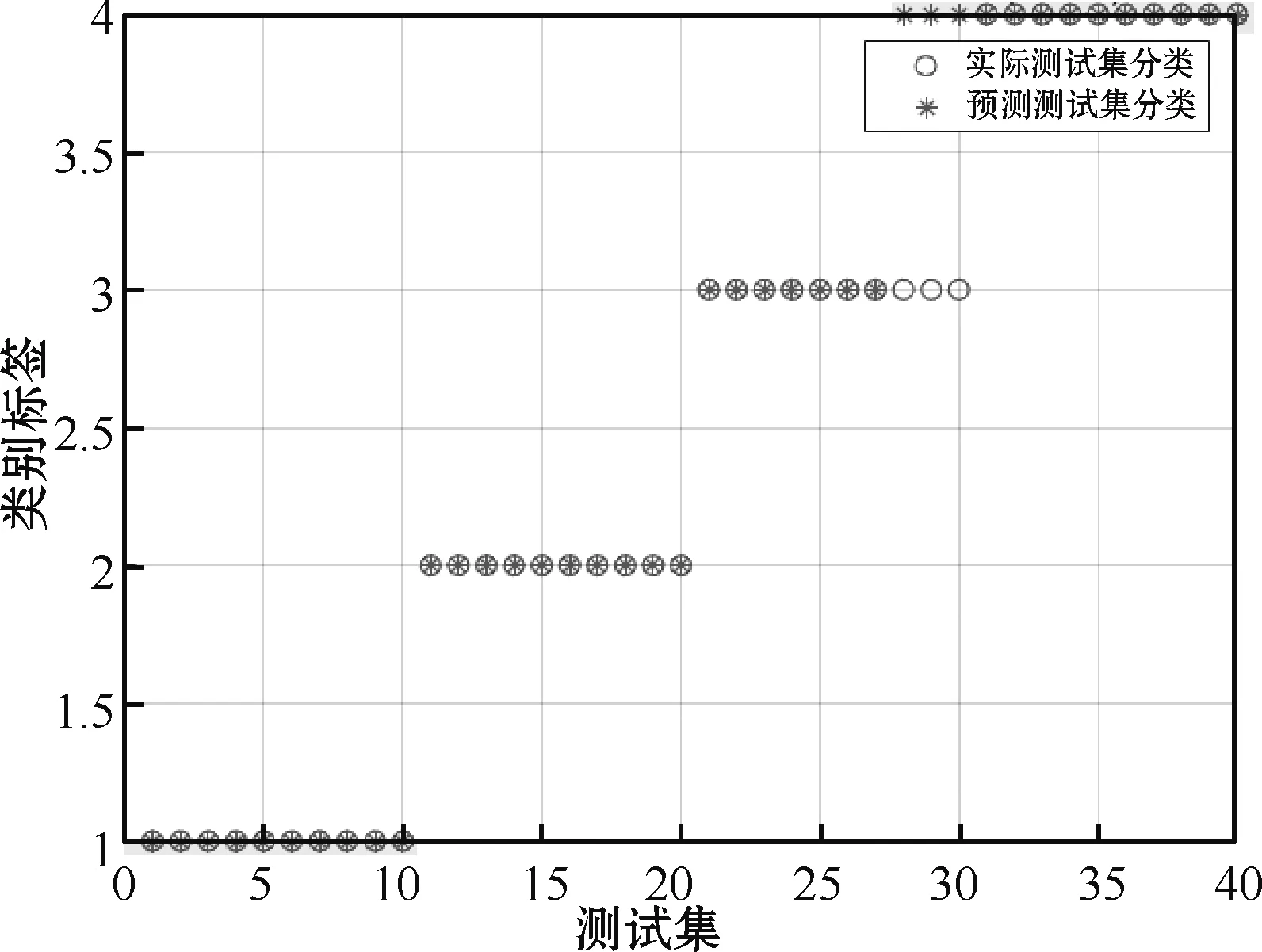
图5 PSO-SVM热评价模型仿真结果
3.2 BP神经网络热评价模型仿真
在保持训练集和测试集与PSO-SVM模型相同的情况下,建立BP神经网络滚珠丝杠热评价模型,并进行仿真。普通BP神经网络建立的数控机床滚珠丝杠热评价模型仿真结果如图6所示。
从图6可以看出,普通BP神经网建立的模型分类的准确率只有75%,出现了多处误差。
3.3 FPSO-BP模型仿真
沿用PSO-SVM模型和BP神经网络的数据集建立分数阶粒子群优化BP神经网络热评价模型(FPSO-BP)。通过设置不同FPSO参数,进行多次试验后,设置种群数量为30,迭代次数为20,具有最优效果,分数阶粒子群迭代结果如图7所示。使用最优参数对BP神经网络的权值和阈值进行优化,建立基于FPSO-BP神经网络的滚珠丝杠热评价模型,利用建立好的数据集进行仿真验证,仿真结果如图8所示。

图7 粒子群迭代结果

图8 FPSO-BP热评价模型仿真结果
由图7可知,粒子适应度值在16代时达到预期。由图8可知,FPSO-BP模型准确率达到97.5%,仅在良等级分类中出现了1处误差,分类效果较好。
3.4 误差分析
对于3个模型预测分类出现的误差,分析其可能的原因如下:1)受到训练时间和计算机内存的限制,使用训练数据的数量不能使模型训练达到理想效果;2)数据间差距不明显,仿真计算时出现误差;3)在整理结果取整时出现误差。
由以上仿真分析可知,PSO-SVM模型与FPSO-BP神经网络模型都表现出较好的准确性;BP神经网络模型准确率较低,在解决分类问题时表现不好。
4 结束语
根据轴承座的温度变化趋势和滚珠丝杠的温度变化趋势相同,采用轴承座及丝杠螺母的温度变化数据取平均值作为滚珠丝杠温度的替代,利用3种不同网络建立了滚珠丝杠热评价模型。通过对3种不同网络在相同数据集下进行训练和仿真,得出PSO-SVM和FPSO-BP神经网络模型具有较高的准确率。本文仅以温度作为参数,未考虑机床的热变形、冷却条件、环境等因素,因此提出的模型仍有缺陷,在今后的研究中应对模型进行全面考虑,建立更贴近实际工况的热评价模型。

