一种基于序列到序列模型的时间序列插补
周 茜,向 维
(北京信息科技大学 自动化学院,北京 100192)
0 引言
多变量时间序列包含多个数据流,这些数据流反映了复杂系统的多种特征参数随时间的变化[1]。每一个特征除了有其自身时间趋势之外,不同的特征之间还相互关联[2]。多变量时间序列数据主要作为历史演变信息来预测复杂系统的未来状态,从而帮助人类做出明智的决策。然而,在实际情况中,由于通信错误、传感器故障等原因,多变量时间序列数据中通常存在缺失数据[3]。缺失值的存在会减少关于复杂系统的未来状态的重要信息,从而增加了预测任务的难度[4]。因此,开发有效的多变量时间序列插补方法是一个重要的研究课题。
缺失数据的插补方法始于统计概率分析,通过分析时间序列的概率分布来获取缺失值的相关信息,从而修复缺失值。例如Qu等[5]利用概率主成分分析(probabilistic principal component analysis,PPCA)方法来预测交通流中丢失的数据。但是,PPCA对时空相关性的提取并不完全适用,导致插补性能降低。Fekade等[6]提出了一种概率矩阵分解(probabilistic matrix factorization,PMF)方法,通过使用相关传感器的数据来填充不完整的数据。PMF利用了在同一时间点从不同传感器收集的测量值之间的相关性,但是忽略了时间相关性。门控递归单元(gated recurrent unit,GRU)和长短期记忆网络(long short-term memory,LSTM)等循环神经网络(recurrent neural network,RNN)具有出色的长期时间依赖性模拟能力,因此被广泛应用于时间序列插补中。Zhang等[7]提出了一种基于LSTM的序列到序列插补模型(sequence-to-sequence imputation model,SSIM),用于修复无线传感器网络中的连续缺失值。但是,SSIM假设输入的多变量时间序列中的所有数据流都具有相同的丢失率[8],且需要完整的数据集进行模型训练。
大多数现有的时间序列插补方法都假设信号是以固定的时间间隔采集的,然而,许多真实的时间序列信号是不规则采样的[9]。例如,在医疗保健系统中,患者的信息是在患者来访时获取的,而不是每次就诊都进行检测。与定期收集的多变量时间序列数据的插补相比,由于缺失数据的模式复杂,在不规则采样时间序列中修复缺失值更具挑战性。Yoon等[10]提出了一种具有插值块和插补块的多方向递归神经网络(multi-directional recurrent neural network,M-RNN)用于处理医学应用中不规则采样的多变量时间序列中的缺失数据。但是,M-RNN是基于顺序存储的,因此当存在缺失值时,无法有效地训练[11]。另外,如何恰当地考虑时间相关性和变量相关性对插补准确度至关重要。
1 模型设计
本文提出了一种新的深度学习网络结构,称为连续初始化序列到序列模型(successively initialized sequence-to-sequence model,SISSM),其由编码器和解码器网络组成。编码器是一个前向循环神经网络层,主要负责提取历史信息。解码器是一个双向递归结构,其后向循环神经网络层使用编码器的输出作为初始状态,而后向层的最后一个状态用以初始化前向层的隐藏状态。因此,在解码器中,后向层使用历史信息插补最后一个时间步的缺失值,而前向层基于未来信息计算第一个时间步的估计值。这种隐藏状态初始化方法能够减少误差沿着生成序列的累积,以提高估计缺失数据的精度。在编码器中,提出了一个交叉回归方法,利用时间域和传感器域的相关性来学习多变量时间序列缺失值的可训练替换值。该编码器使用具有交叉回归的GRU(GRU with cross-regression,GRU-CR)作为其递归分量来学习历史信息。解码器的递归分量由一个插补块(imputation block,IB)和一个GRU组合而成,简称为IB-GRU。由于隐藏状态只包含过去或将来的信息,IB的引入可通过结合当前时间步长变量间的相关性和时间依赖性来计算缺失值估计。IB-GRU使得该网络能够识别多变量时间序列的复杂模式,从而提高缺失值估计的准确度。
在模型的训练阶段,当输入变量的值存在时,SISSM通过逼近输入变量的值来学习一个复杂的拟合函数,而当输入变量缺失时对其进行插补。因此,SISSM可以使用不完整的时间序列数据集进行训练。此外,SISSM能够修复不规则采样的多变量时间序列中的随机和连续缺失数据。为了验证SISSM的优越性,将在两组临床数据集上与4个最先进的插补模型的插补结果进行比较。
1.1 公式符号说明
定义X=[x1,x2,…,xT]∈RN×T为一个长度为T具有N个变量的多变量时间序列,其中xt=[x(1,t),x(2,t),…,x(N,t)]T表示所有N个传感器的第t个观测值。定义s=[s1,s2,…,sT]为时间戳向量,其中st∈R表示获得第t个观测值的实际时间。定义一个指示矩阵为M,其每个元素m(i,t)由X中的相应元素是否存在来决定。如果x(1,t)存在,m(i,t)为1,否则为0。由于传感器数据并非总是以相同的时间间隔收集且一些观测值可能会从连续的时间段中丢失,因此定义Δ∈RN×T为自上次观测到值的时刻至当前时刻所经过的时间。当t=1时,Δ的元素δ(i,t)=0;当t>1时,δ(i,t)=st-st-1+(1-m(i,t-1))δ(i,t-1)。
1.2 模型结构


图1 连续初始化序列到序列模型(SISSM)结构
1.2.1 门控递归单元
由于RNN能够自然地处理可变长度序列,且其在所有时间步长上共享参数,这大大减少了需要学习的参数个数。在RNN的变体中,使用了门控递归单元(GRU)。GRU的网络结构如图2所示,其具有复位门rt和更新门zt,用以在时间步t处控制隐藏状态ht,更新公式如下:

图2 CRU网络结构
rt=σ(Wrxt+Urht-1+br)
(1)
zt=σ(Wzxt+Uzht-1+bz)
(2)
(3)
(4)
式中:矩阵Wz、Wr、W、Uz、Ur、U和向量bz、br、b为模型训练参数;σ为Sigmoid激活函数;⊙表示逐元素相乘。
1.2.2 GRU-CR编码器
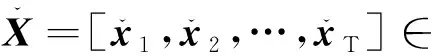
(5)
式中:φ为激活函数;U、V和B为可优化的模型参数。在时间序列数据中,附近观测到的测量值对缺失值的依赖性将随着时间的推移逐渐消失。因此,为每个变量引入了状态衰减率,用ηt∈RN表示。ηt的值取决于自上一次观测到数据的时刻至当前时刻t所经过的时间δt。时间越长,衰减率越小。根据牛顿冷却定律[12],本文使用负指数率随δt增加单调减小ηt,即
ηt=e-(Wηδt+bη)
(6)
式中Wη和bη为通过训练获得的模型参数。状态衰减率ηt用于在计算新状态ct之前衰减前一个隐藏状态ct-1,即
(7)
(8)

(9)
1.2.3 双向IB-GRU解码器
在解码器网络中,每个时间步t的输出为该时间步的测量值估计值。由于RNN在序列的不同时间步长之间共享参数,因此可能无法捕获不规则的丢失模式。另外,估算值仅与时间相关,而与其他传感器的当前观测值无关。为了解决这些问题,本文通过在传统的GRU中引入插补块以改进GRU的基本结构,称之为IB-GRU网络,其结构如图3所示。

图3 IB-GRU网络结构
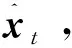
ξ(at)=xt⊙mt+at⊙(1-mt)
(10)
式中at为估计值。在IB中,前一个隐藏状态ht-1首先被衰减,然后使用全连接神经网络基于时间信息计算输出估计值zt,即
(11)
(12)
式中Wh和bh为可训练的模型参数。为了增强多重相关性模拟能力,首先用zt中的相应值更新xt中的缺失值。然后,加入一个全连接神经网络,基于当前时间下的变量之间的相关性计算输出估计值ot,即
ot=φ(Woξ(zt)+bo)
(13)
式中Wo和bo为可学习的模型参数。Wo的对角线元素设为零,因此ξ(zt)中的第i个变量不用于估计o(i,t)。
λt=σ(Wλδt+Uλmt+bλ)
(14)
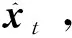
(15)
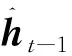
(16)
2 数据集及评价方法
2.1 数据集
PhysioNet数据集[13]是PhysioNet Challenge 2012的公开临床数据集,包含了在重症监护室中的12 000份患者记录。在这个数据集中,每个病人的记录包含42个变量,包括血压、心率和体温等。从这42个变量中,提取了35个变量,这些变量是在病人进入重症监护室后48 h内不定期取样的。对于数据预处理,本文将每个变量的数值标准化,使其均值为0和方差为1以进行稳定训练[14]。
MIMIC-III数据集[15]的所有临床护理数据来自大约60 000名患者的住院记录,这些记录是从2001年到2012年在贝斯以色列女执事医疗中心的重症监护室收集的。在整个MIMIC-III数据集中,只保留了15岁以上、单次入院时间超过48 h但少于30 d的患者,删除了没有图表事件数据和48 h内少于50次测量的临床记录。因此,经过数据预处理后,数据集包含了21 250名有足够观察值的患者的记录,每个样本包含96个不同的生理变量。
2.2 评估指标和对比方法
本文采用两个指标评估每个模型的数据插补性能,即均方根误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE)。两者都常在统计模型评估中用作预测值和观测点坐标之间距离偏差的有效度量。由于RMSE是基于误差平方和的计算,因此会放大较大的误差且对异常值非常敏感[16]。MAE是误差的真实值,与RMSE相比,异常值对MAE的影响较小。
为了验证SISSM网络的优越性及有效性,本文将提出的模型与其他文献中的4种方法进行了比较,即SSIM[7]、M-RNN[10]、GRU-D[17]和LIME-LSTM[18]。M-RNN基于多方向递归神经网络估计临床时间序列的丢失数据,其包含了一个双向RNN结构。SSIM是一种基于序列到序列模型的数据插补方法,用于在无线传感器网络中修复丢失的数据。GRU-D是一种基于GRU的深度学习模型,其利用多变量时间序列插补和分类中的时间衰减效应学习衰减因子,将最近的观测值与每个变量的经验平均值相结合来替换缺失值。LIME-LSTM是线性记忆向量递归神经网络(linear memory vector recurrent neural network,LIME-RNN),该网络引入了一个残差和向量作为所有先前隐藏状态的加权和,以增强模型的时间模拟能力。
3 仿真结果与分析
本文选择了两个具有较高丢失率的临床数据集用以验证所提出模型的插补性能。首先任意删除10%已有的测量值作为评估的插补标签值,然后使用这两个数据集对训练好的SISSM及4个对比模型进行测试。为了评估模型性能的稳定性,每个模型的仿真实验以不同的随机初始权重进行10次。在两个数据集上10次实验的插补误差的最小值、最大值、均值和方差如表1、2所示。
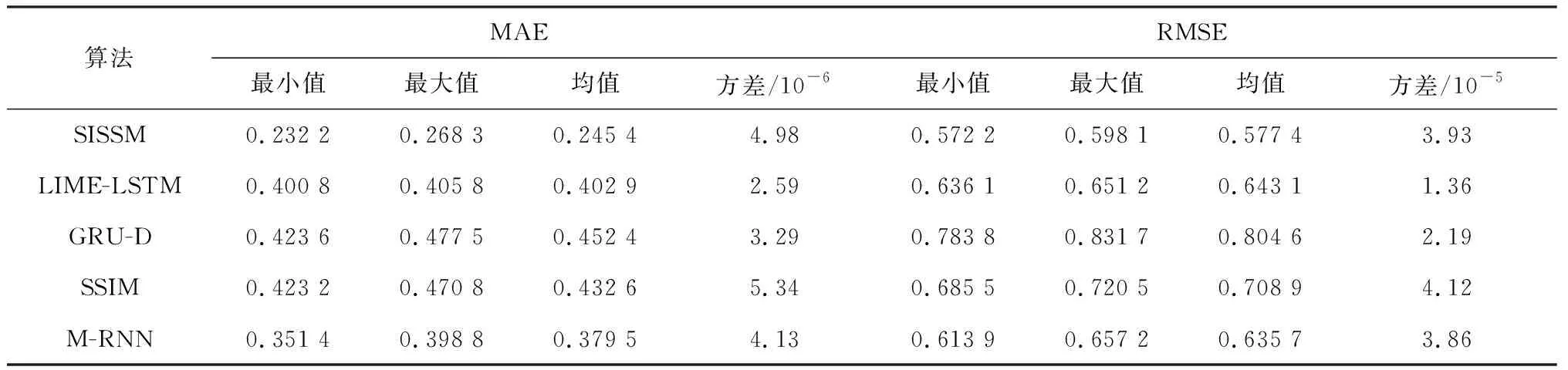
表1 PhysioNet数据集下5种算法的插补误差比较
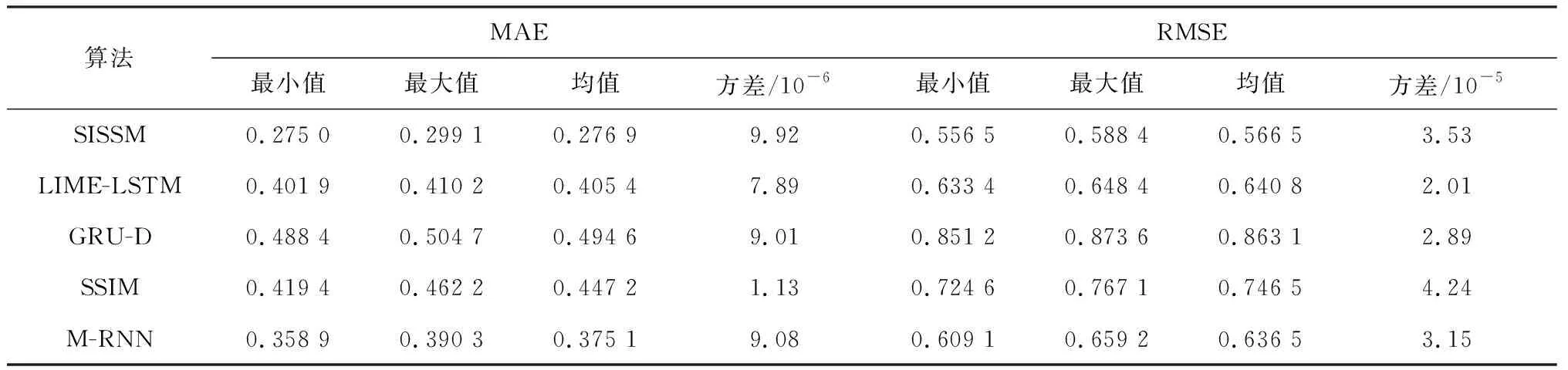
表2 MIMIC-III数据集下5种算法的插补误差比较
由表1、2可知,5种算法都可以插补多变量时间序列的缺失值,但插补的效果不尽相同,其中SISSM获得了最低的插补误差即最好的插补准确度。SISSM的模型稳定性并不好,其10次实验的MAE和RMSE的方差仅小于SSIM的插补误差的方差。之所以本文所提出模型的插补性能最优,是因为在编码器中引入了交叉回归器,从而加强了模型对时间依赖性和变量相关性的模拟能力,在解码器中采用了双向循环神经网络结构以利用过去和将来的数据点来重建丢失的数据点,另外SISSM还考虑了误差累积以及训练过程中采样间隔的不规则性对缺失值的影响。以上做法增加了模型插补准确度,但同时也增加了模型复杂度,需要大量样本训练获得模型参数,这也将影响模型的稳定性。虽然SSIM和M-RNN也采用了双向循环网络结构,但是它们的插补误差较大且模型稳定性欠佳。SSIM被用于修复含有连续缺失值的水质数据,并假设所有的时间序列含有一样的丢失率,这使得SSIM很难适用于其他领域的数据集,尤其是像PhysioNet和MIMIC-III这种采样时间间隔不规则的数据集。M-RNN是用以解决不规则的临床医疗数据的数据丢失问题,考虑了双向插补和变量相关性,因此可以较好地修复本文采用数据集的丢失值。对于其他两个单层的前向循环神经网络结构LIME-LSTM和GRU-D,LIME-LSTM的模型稳定性最优但插补误差比SISSM和M-RNN都高,GRU-D插补结果最差。GRU-D采用隐式估算缺失值的方法(即仅专注于优化预测误差),不能准确地修复缺失值。LIME-LSTM忽略了变量相关性,因此其插补过程并没有充分利用时间和变量维度间的关系,对插补准确度产生了负面影响。
为了评估数据缺失率对模型插补准确度的影响,随机剔除了10%、15%、20%、25%、30%、35%、40%、45%和50%的已有数据,然后在不同缺失率的测试集上验证模型性能。每个模型的仿真实验以不同的随机初始权重进行10次,最终以10次实验结果的均值作曲线图。图4和图5分别呈现了在PhysioNet数据集和MIMIC-III数据集下5种算法的MAE随丢失率增加的变化以及SISSM相对于其他模型所获得的增益变化。
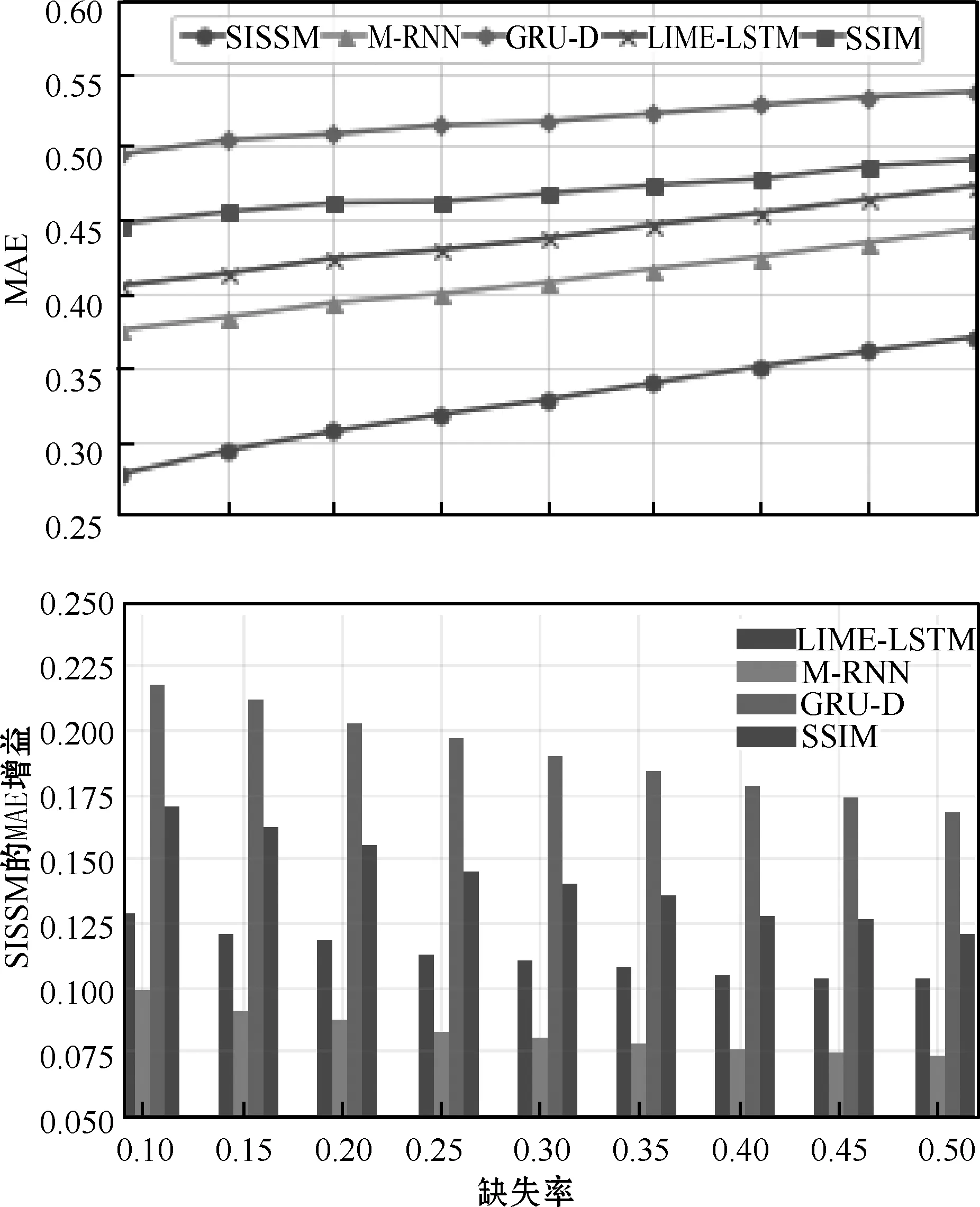
图4 在PhysioNet数据集下5种算法的MAE随缺失率增加的变化以及SISSM相对于其他模型所获得的增益变化
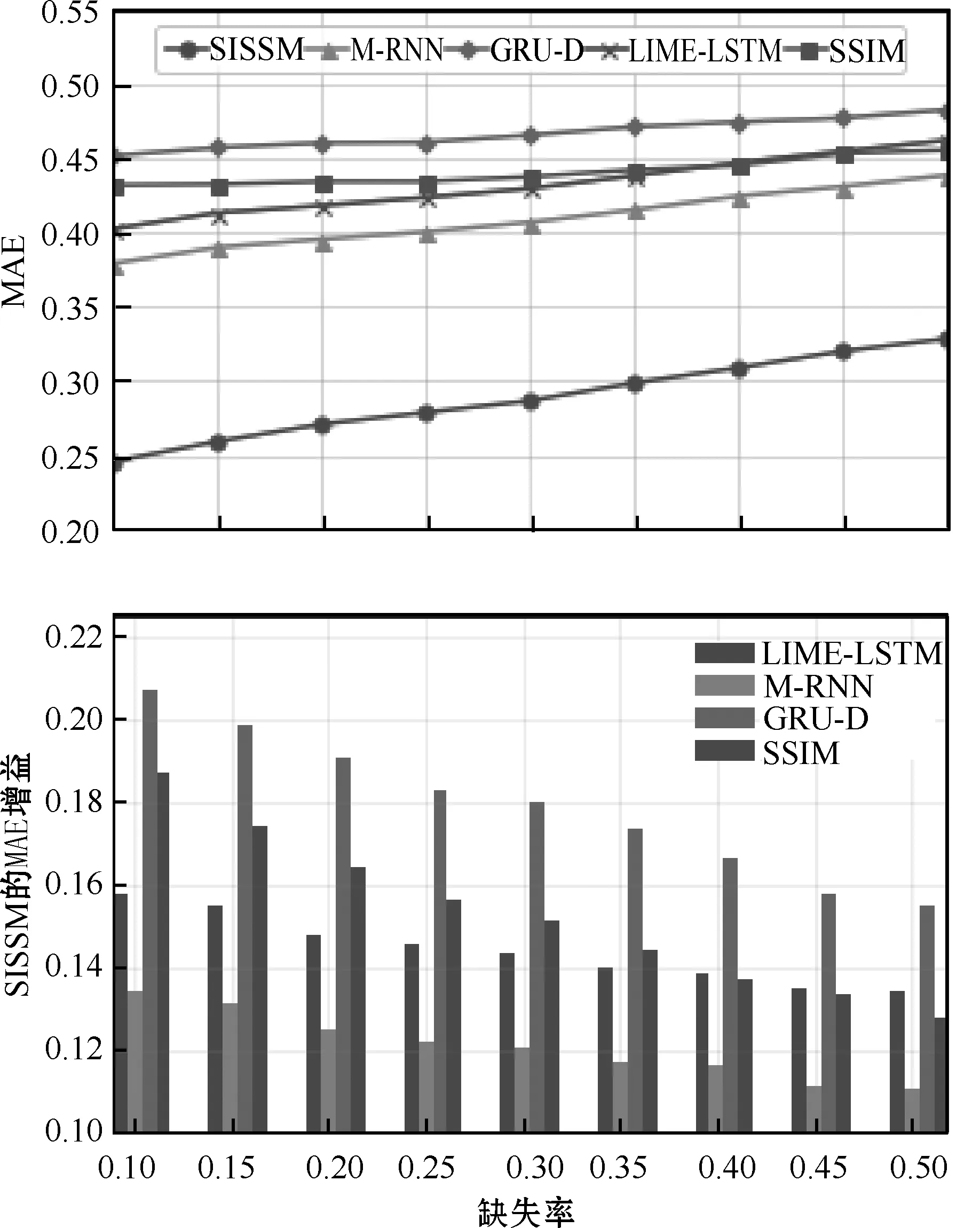
图5 在MIMIC-Ⅲ数据集下5种算法的MAE随缺失率增加的变化以及SISSM相对于其他模型所获得的增益变化
从图4和图5可以看出,随着缺失率的升高,5种算法插补数据的MAE都随之增大,SISSM在不同的缺失率下插补效果较为显著,插补的MAE比其他4种小。在缺失率较低时LIME-LSTM的插补效果优于SSIM,但随着缺失率的升高SSIM的效果则有明显改善,且在MIMIC-III数据集上效果要优于LIME-LSTM。SISSM和M-RNN的插补效果分别比GRU和LIME-LSTM的效果好,很好地说明了在学习的过程中双向循环神经网络结构能够更多地捕捉时间依赖性,从而更好地实现时间序列的缺失值插补。另外,SISSM在4个对比模型上所获得的增益随着缺失率的增加而减小。由此可见,所提出模型应对较高缺失率时,插补效率有所降低,但其插补误差仍然比其他4种算法小很多。综上所述,SISSM网络相对于其他插补模型能更准确地估计多变量时间序列的丢失值,且即使在丢失数据率很高的情况下也能提供较好的插补性能。
4 结束语
由于不可避免的通信故障或传感器故障,多变量时间序列通常包含缺失值。本文提出了一种基于序列到序列模型的多变量时间序列插补方法SISSM,它由GRU-CR编码器和双向IB-GRU解码器组成。在SISSM模型中,提出了一种状态初始化方法,该方法有助于减少误差累积并提高插补精度。设计了交叉回归器用来获得原始多变量时间序列中的缺失值的可训练替换值,以便编码器能够从不完整的多变量时间序列数据中学习历史信息代表性。在GRU中引入了一个插补块,以根据不同时间段的值之间的相关性和相同时间点处的变量相关性计算得出缺失值的估计值。为了验证SISSM的插补效果,采用了两个真实的多变量时间序列数据集对其进行了仿真实验。实验结果表明,与其他的算法相比,本文所提出的模型具有更好的插补结果,并且在较大的丢失率范围内插补准确度依然是最高的。

