高次非球面镜面低温面形拟合方法研究

童卫明 白绍竣

高次非球面镜面低温面形拟合方法研究

童卫明 白绍竣

（北京空间机电研究所，北京 100094）

高次非球面在空间红外低温光学中应用广泛，传统的球面拟合方法不适用于高次非球面低温面形拟合，而Zernike多项式拟合法因涉及像差理论拟合过程复杂在结构设计人员中应用较少。针对上述情况，文章提出了一种能够快速拟合低温高次非球面镜面面形的方法。首先，基于高次非球面展开式可以精确表达成偶次多项式建立了偶次多项式拟合方程，直接拟合低温非球面面形；非球面裸镜低温自由变形算例验证表明，文章提出的方法能够很好地拟合高次非球面低温面形，拟合残差达到9.15×10–5(=0.6328μm)。将该方法应用到低温透镜支撑结构设计中进行面形拟合，结果显示低温变形引起的面形误差由采用柔性支撑结构之前的0.0217下降到0.0018，进一步支撑了提出的算法的有效性。

高次非球面 低温 面形拟合 柔性卸载 空间光学

0 引言

在光学系统中使用高次非球面可以减小像差，同时也可以减少光学元件的数量。为提高成像品质、减小相机尺寸，航天相机光学系统中应用了大量高次非球面设计。随着空间红外低温光学技术的发展，高次非球面镜面已应用到JWST、EUCLID等载荷低温镜头设计中[1-2]。由于支撑结构材料同透镜或反射镜材料线膨胀系数不一致，工作温度从常温降至低温时两种材料变形不同会使镜面面形变差，需要采用无热化胶层厚度设计、柔性支撑或弹性支撑等手段保证面形[3-6]。在低温镜头光机结构设计中，需要采用有限元方法计算低温下镜头变形，然后进行面形拟合评价支撑结构变形对面形的影响，迭代改进支撑结构直至镜面面形误差满足指标要求。

镜面变形包括刚体位移和面形误差[7]。计算刚体位移时，采用齐次坐标变换建立变形后节点和变形前节点之间坐标关系，然后利用最小二乘法求解线性方程组，获得镜面平移、倾斜和旋转[8]。去除刚体位移后剩余变形即为面形误差，拟合面形误差的方法主要包括球面方程拟合法和Zernike多项式拟合法[9-10]。Zernike多项式拟合法其系数与Seidel像差存在对应关系，在SigFit面形拟合软件和光机热集成分析的数据交互中应用比较广泛[11-12]；球面方程拟合方法与实际干涉检验过程接近，在重力、胶层固化、小幅度温升等工况下的镜面面形拟合中获得广泛应用[13]。

针对低温镜面面形拟合，当镜面为球面时，采用球面方程拟合和Zernike多项式拟合都可获得较高精度。球面方程拟合后剩余误差可以认为是支撑结构引起的面形变化；Zernike多项式拟合时，从常温到低温顶点曲率半径的变化会引起离焦、球差和高阶球差的变化，将这些项去除之后的残差才代表支撑结构引起的面形变化[14]。当镜面为高次非球面，采用球面方程拟合时，拟合残差较大，无法评价支撑结构引起的面形变化；用Zernike多项式拟合时，需要对各项拟合系数进行判断，然后才能得到支撑结构引起的面形误差，过程比较复杂，结构设计人员一般很少选用。基于上述实际，本文提出采用偶次多项式拟合高次非球面低温面形、拟合残差代表支撑形式引起的面形变化的一种新方法。

1 拟合理论

1.1 高次非球面方程展开式

高次非球面方程采用右手笛卡尔坐标系，原点与高次非球面顶点重合，光轴为轴。具体表达式为

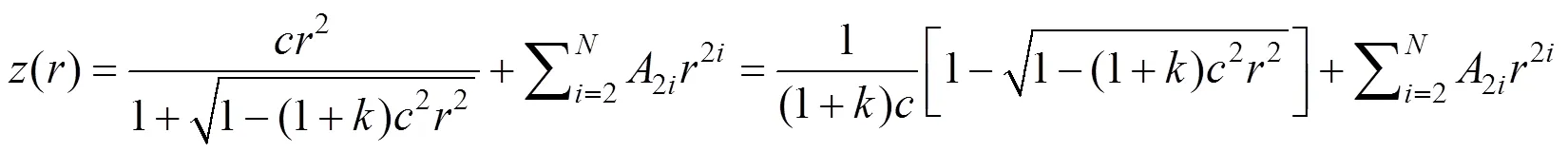
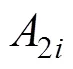
根据文献[15]高次非球面表达式可以展开为偶次多项式，即

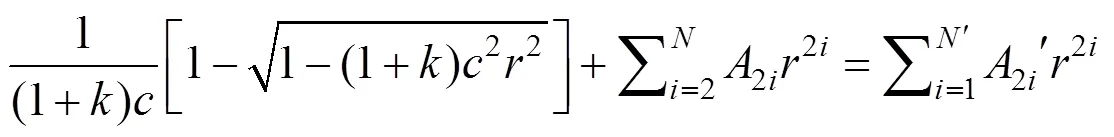
表1 镜面参数和几何尺寸

Tab.1 Mirror surface parameters and dimensions

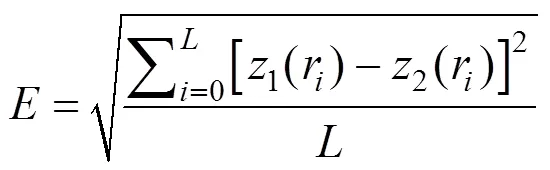
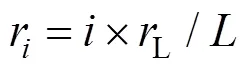
表2 展开误差

Tab.2 Polynomial fitting error

1.2 拟合算法

高次非球面低温面形拟合算法的实现，首先是采用有限元方法分析低温下镜面变形，然后拟合镜面刚体位移，去除刚体位移后进行镜面面形拟合。

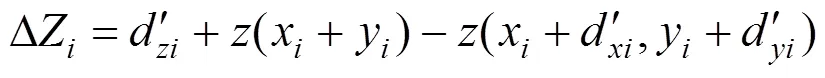
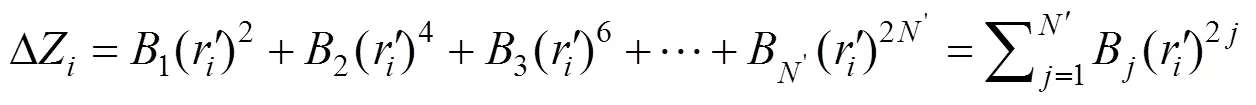
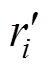
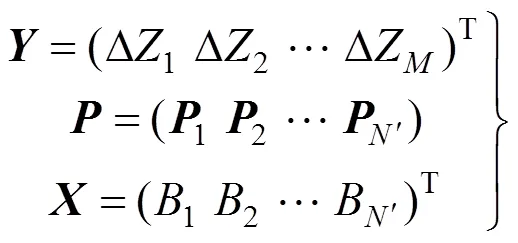
经计算，偶次多项式基底在镜面离散网格点上不满足正交性，直接求解式（7）时会出现病态，计算误差很大，因此，本文采用Gram-Schmidt正交化方法求解式（7）[18]。首先，根据偶次多项式基底构造在镜面离散网格点上正交的多项式基底

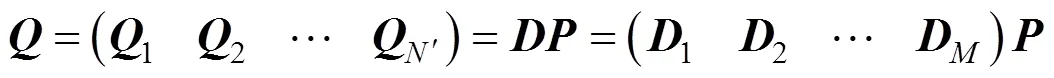
式（8）中矩阵由Gram-Schmidt正交化方法计算，具体为

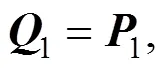
据此构造出矩阵，由于和具有相关性，式（7）可转化为

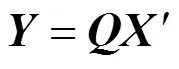
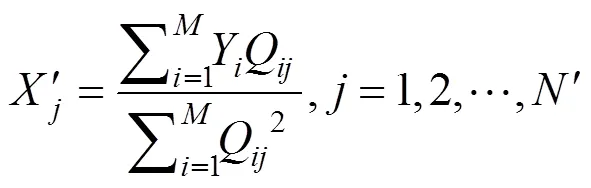
根据和的递推关系[18]，式（10）可以表示为

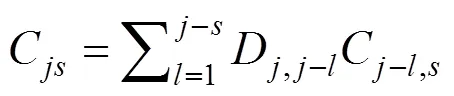
对比式（7），可得

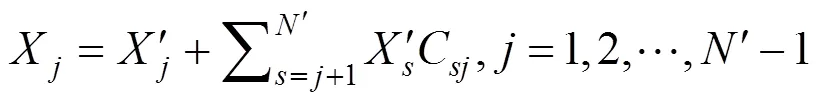
至此，完成用偶次多项式拟合矢高变化的过程，拟合残差即为面形误差。

2 测试算例

当偏心率为0，非球面系数为0时，式（1）所示方程退化为球面。根据文献[16]，球面受温度作用产生自由变形，顶点曲率半径变化公式为

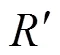
根据式（2），球面温度从293.15K变化到200K时偶次多项式展开系数表达式分别为

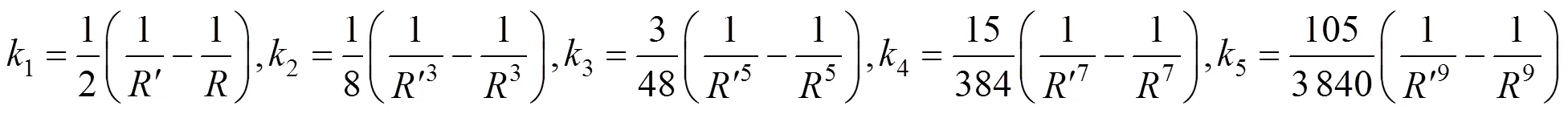
通过有限元计算得到透镜低温变形位移云图如图1（a）所示，非球面失高变化云图如图1（b）所示。透镜因自由变形向中心收缩时，非球面顶点曲率半径和非球面系数都会发生变化，导致失高发生变化，离中心位置越远失高变化越大。球面的失高变化云图和非球面的形状相似，这里不做显示。

提取球面节点位移，刚体位移拟合结果显示只有方向平移–0.005 7mm。去除刚体位移后采用偶次多项式拟合矢高变化量，拟合系数如表3所示。

表3 球面矢高变化拟合系数

Tab.3 Fitting results of spherical sag displacement

球面直径170mm，由理论系数可知8和10项对矢高变化的贡献非常小，前三项拟合系数和理论值十分接近，最终算得拟合残差为9.6×10–5，拟合精度优于0.1nm，表明采用偶次多项式能够精确地拟合球面失高变化。

提取非球面节点位移，刚体位移拟合结果显示只有方向平移–0.005 7mm，和球面拟合结果一致，因为球面和非球面在同一个实体上，刚体位移拟合结果应相同。去除刚体位移后采用偶次多项式拟合矢高变化量，拟合系数如表4所示，拟合残差9.15×10–5。由于自由变形，镜面面形误差理论上为0，说明采用偶次多项式能够精确地拟合高次非球面镜面低温面形。

表4 非球面矢高变化拟合分数

Tab.4 Fitting results of aspherical sag displacement

3 工程应用

本节将基于偶次多项式的高次非球面低温面形拟合方法应用到低温透镜支撑结构设计中。由于透镜材料、支撑结构材料和胶粘剂的线膨胀系数存在差异，从常温到低温工作时由于变形不一致产生应力会影响透镜面形。只采用无热化胶层厚度设计[19-20]时，经常会由于胶层过厚影响力学性能和支撑稳定性，因此，一般采用柔性卸载支撑结构，将透镜和镜框之间胶结，然后在镜框粘接面径向加工柔性结构以卸载变形不一致产生的应力。两种透镜支撑结构如图2所示。

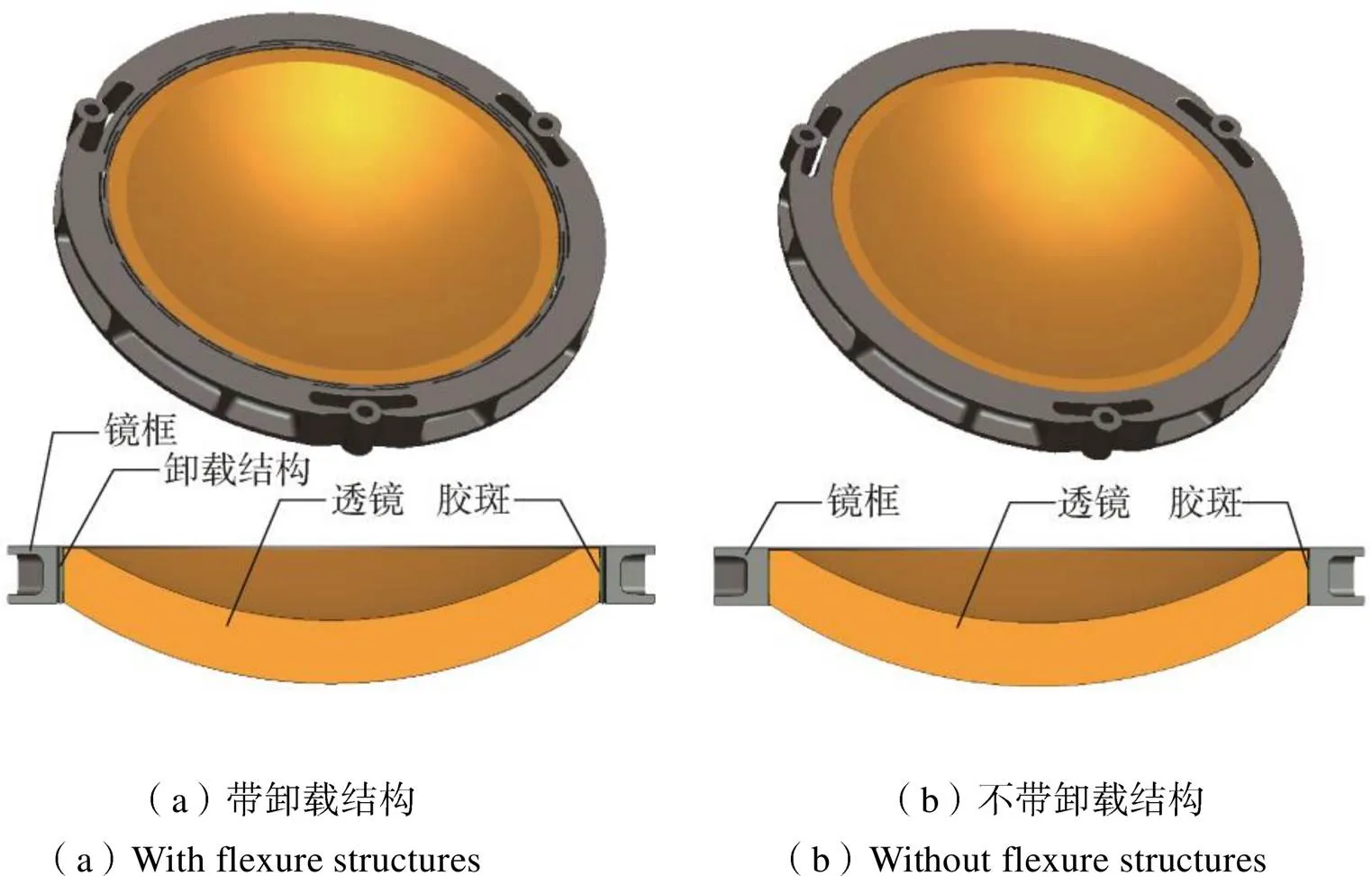
图2 两种透镜支撑结构

采用二阶四面体单元建立两种支撑结构有限元模型，胶斑和透镜及镜框连接采用节点重合建模。相关材料属性参数见表5。采用MSC Nastran惯性释放技术，分析温度从293.15K降到200K透镜的结构变形，两种支撑结构节点位移云图如图3、4所示。两种结构透镜和镜框变形都是向透镜中心收缩，由于透镜材料和镜框材料线膨胀系数存在差异，自由变形时两者的收缩量会存在差异，若镜框采用卸载结构，柔性结构通过局部变形使透镜能够接近自由收缩，图3中可明显观察到卸载结构的局部变形。

表5 材料属性参数

Tab.5 Material properties

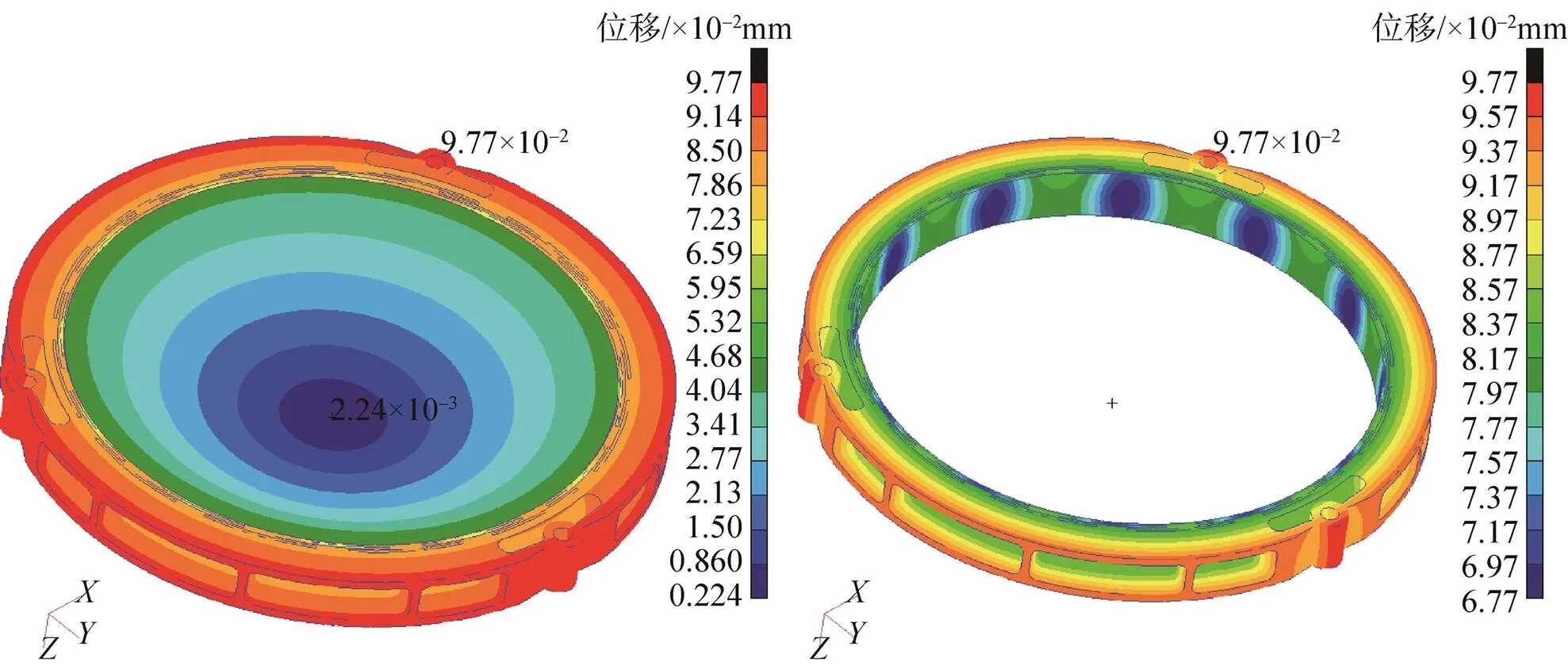
图3 带卸载结构透镜组件和镜框变形位移云图

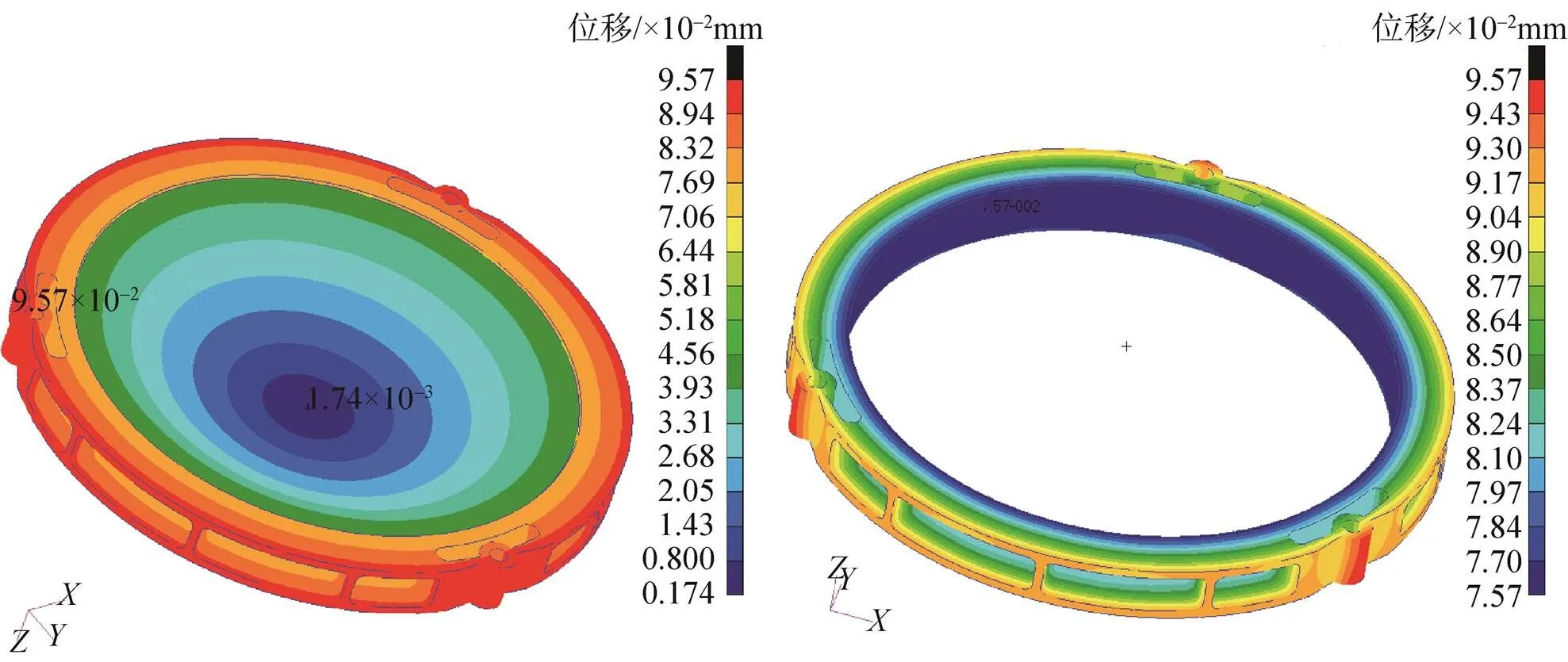
图4 无卸载结构透镜组件和镜框变形位移云图

提取非球面镜面节点位移进行刚体位移拟合，去除刚体位移后再采用偶次多项式拟合矢高变化，刚体位移拟合结果如表6所示。偶次多项式拟合系数及拟合后残差如表7所示。由表7结果可知，采用柔性卸载结构时，镜框柔性环节很好地卸载了热应力，对非球面镜面面形影响很小，只有0.0018。当没有采用柔性卸载环节时，热应力引起非球面面形误差达到0.0217。透镜低温面形拟合结果表明采用偶次多项式拟合高次非球面面形，剩余残差能够很好地评价支撑结构对面形的影响，能够应用于实际低温镜头支撑设计仿真分析。

表6 刚体位移拟合结果

Tab.6 Fitting results of Rigid motion

表7 非球面镜面面形拟合结果

Tab.7 Aspherical surface error fitting results

4 结论

本文提出一种高次非球面镜面低温面形拟合方法，即采用偶次多项式拟合变形后镜面矢高变化，拟合残差即代表面形误差变化。该方法可解决球面拟合方法无法拟合高次非球面低温变形问题，同时相比Zernike多项式拟合方式其结果更容易判读，所有残余像差都包含在拟合误差中。裸镜低温自由变形算例表明偶次多项式能够很好地拟合非球面低温面形，非球面拟合残差达到9.15×10–5，同时该方法也适用于球面低温变形拟合。将文本提出的方法实际应用到低温透镜支撑结构设计中，通过设计 柔性支撑结构，低温下支撑结构引起的面形误差由0.021 7下降到0.001 8，面形拟合结果显示算法有效。

[1] RYDER L A, OSCHMANN J M, DE GRAAUW M W M, et al. Cryogenic Test Results of Engineering Test Unit Optical Components of Near Infrared Camera for the James Webb Space Telescope[C]//Proceedings of SPIE,Space Telescopes and Instrumentation 2008: Optical, Infrared, and Millimeter. [S.l.]: SPIE, 2008: 701010-1-9.

[2] GAL C, REUTLINGER A, BOESZ A, et al. Test Results of High Precision Large Cryogenic Lens Holders[C]//Proceedings of SPIE, Modern Technologies in Space and Ground-based Telescopes and Instrumentation II. Bellingham, WA, USA : Society of Photo-Optical Instrumentation Engineers, 2012, 84500P: 1-12.

[3] MONTI C L. Athermal Bonded Mounts: Incorporating Aspect Ratio into a Closed-form Solution[C]//Proceedings of SPIE, New Developments in Optomechanics. [S.l.]: SPIE, 2007, 6665: 666503-1.

[4] HORN C L, HOLMES H C, LAPICZ D N, et al. Cryogenic Bonding for Lens Mounts[C]//Conference on Astronomical and Space Optical Systems, San Diego, CA, USA, 2010: 743910.1-743910.12.

[5] SMEE S A. A Precision Lens Mount for Large Temperature Excursions[C]//Proceedings of SPIE, Modern Technologies in Space- and Ground-based Telescopes and Instrumentation. [S.l.]: SPIE, 2010, 7739: 77393O.

[6] KVAMME E T, JACOBY M. A Second Generation Low Stress Cryogenic Mount for Space-borne Lithium Fluoride Optics [C]//Proceedings of SPIE, Cryogenic Optical Systems and Instruments XII. [S.l.]: SPIE, 2007, 6692: 66920I.

[7] 田富湘, 何欣. 空间光学遥感器光学镜面有限元分析结果的后处理[J]. 红外, 2014, 35(9): 19-23.

TIAN Fuxiang, HE Xin. Post-processing of FEA Results of Optical Mirrors for Space Remote Sensor[J]. Infrared, 2014, 35(9): 19-23. (in Chinese)

[8] 张军强, 董得义, 吴清文, 等. 光学遥感器镜面面形误差及刚体位移处理方法[J]. 仪器仪表学报, 2011, 32(6): 242-246.

ZHANG Junqiang, DONG Deyi, WU Qingwen, et al. Treatment of Surface Figure Error and Rigid Body Motion for Mirror/Lens in Optical Remote Sensor[J]. Chinese Journal of Scientific Instrument, 2011, 32(6): 242-246. (in Chinese)

[9] 兰斌, 杨洪波, 吴小霞, 等. 接口前处理在光机系统动力学分析和面形优化中的应用[J]. 光学精密工程, 2017, 25(6): 1557-1566.

LAN Bin, YANG Hongbo, WU Xiaoxia, et al. Application of Interface Preprocessing in Opto-mechanical System Dynamics Analysis and Surface Shape Optimization[J]. Optics and Precision Engineering, 2017, 25(6): 1557-1566. (in Chinese)

[10] 杨佳文, 黄巧林, 韩友民. Zernike多项式在拟合光学表面面形中的应用及仿真[J]. 航天返回与遥感, 2010, 31(5): 49-55.

YANG Jiawen, HUANG Qiaolin, HAN Youmin. Application and Simulation in Fitting Optical Surface with Zernike Polynomial[J]. Spacecraft Recovery & Remote Sensing, 2010, 31(5): 49-55. (in Chinese)

[11] GENBERG V, MICHELS G, DOYLE K. Making FEA Results Useful in Optical Analysis[C]//Proceedings of SPIE, Optical Design and Analysis Software II. [S.l.]: SPIE, 2002, 4769: 24-33.

[12] SHAN B Z, GUO B P, NIU H B, et al. Zernike Polynomials for Evaluation of Optical System in Use[C]//Proceedings of SPIE, Optomechanics. [S.l.]: SPIE, 2007, 6723: 67234T.

[13] 董得义, 李志来, 薛东林, 等. 大口径长条形反射镜组件自重变形的仿真与试验[J]. 光学精密工程, 2016, 24(6): 1424-1431.

DONG Deyi, LI Zhilai, XUE Donglin, et al. Analysis and Experiment of Gravity Deformation for Large Aperture Rectangular Mirror Set[J]. Optics and Precision Engineering, 2016, 24(6): 1424-1431. (in Chinese)

[14] CHRZANOWSKI C, FROHLICH C, SHIRGUR B, et al. Design and Structure/Optical Analysis of a Kinematic Mount for the Testing of Silicon Carbide Mirrors at Cryogenic Temperatures[C]//Proceedings of SPIE, Space Systems Engineering and Optical Alignment Mechanisms. [S.l.]: SPIE, 2004, 5528: 204-214.

[15] WAN Z M, QU W J, ANAND A. A Simplified Expression for Aspheric Surface Fitting[J]. Optik, 2017, 140: 291-298.

[16] DOYLE K B, GENBERG V L, MICHELS G J. Integrated Optomechanical Analysis[M]. USA: SPIE Press, 2012.

[17] CORONATO P A, JUERGENS R C. Transferring FEA Results to Optics Codes with Zernikes: A Review of Techniques[C]//Optomechanics 2003, San Diego, CA, USA, 2003, 5176: 1-8.

[18] MALACARA D, CARPIO-VALADÉZ J M, SÁNCHEZ-MONDRAGÓN J J. Wavefront Fitting with Discrete Orthogonal Polynomials in a Unit Radius Circle[J]. Optical Engineering, 1990, 29(6): 672-675.

[19] MONTI C L. Athermal Bonded Mounts: Incorporating Aspect Ratio into a Closed-form Solution[C]//Proceedings of SPIE, New Developments in Optomechanics. [S.l.]: SPIE, 2007, 6665: 66503.

[20] DOYLE K B, MICHELS G J, GENBERG V L. Athermal Design of Nearly Incompressible Bonds[C]//Proceedings of SPIE, Optomechanical Design and Engineering. [S.l.]: SPIE, 2002, 4771: 296-303.

Research on Cryogenic Aspheric Surface Error Fitting Methods

TONG Weiming BAI Shaojun

（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

Aspheric surface is widely used in cryogenic optics for space infrared cameras. The traditional spherical fitting method can not be used for cryogenic aspheric surface error fitting. The Zernike polynomial fitting method is not ideal for structural engineers because of the aberration theory. In view of the above situation, a new method which can fit cryogenic aspheric surface error quickly is proposed in this paper. By analyzing the aspheric equation, it can be accurately expressed to even polynomials. Based on this, a method of fitting cryogenic aspheric surface error with even polynomials is proposed. Fitting equation is established and fitting algorithm is given. Finally, the cryogenic deformation example of lens without support structure shows that the proposed method can fit aspherical surface well and the fitting residual is 9.15×10–5(=0.632 8μm). At last, the method proposed is applied to cryogenic lens design. Surface error fitting results show that aspheric surface error is reduced from 0.027 1to 0.001 8when flexure structure is used.

aspheric; cryogenic; surface error fitting; flexure; space optics

TN219

A

1009-8518(2021)03-0079-09

10.3969/j.issn.1009-8518.2021.03.009

2020-10-29

国家重大科技专项工程

童卫明, 白绍竣. 高次非球面镜面低温面形拟合方法研究[J]. 航天返回与遥感, 2021, 42(3): 79-87. TONG Weiming, BAI Shaojun. Research on Cryogenic Aspheric Surface Error Fitting Methods[J]. Spacecraft Recovery & Remote Sensing, 2021, 42(3): 79-87. (in Chinese)

童卫明，男，1989年生，2015年获北京航空航天大学航空工程专业硕士学位，工程师。研究方向为航天遥感器光机结构设计与分析。E-mail：TWM08Acoustics@163.com

（编辑：夏淑密）