Hom-δ-Jordan李色代数的构造与交换扩张

马丽丽，韩 旸

(齐齐哈尔大学理学院，黑龙江 齐齐哈尔 161006)

1 预备知识

Okubo和Kamiya研究了δ-Jordan李超代数，其是李超代数的推广.当δ=1时，δ-Jordan李超代数即为李超代数[1-2].陈良云等[3]研究了Hom-δ-Jordan李超代数的表示和形变；Scheunert[4]从纯数学角度研究了李色代数，并得到了李色代数的PBW定理和Ado定理.随后，学者们讨论了李色代数的表示理论[5]，证明了李色代数的Engel定理[6]，研究了李色代数的广义导子和T*-扩张[7-8].目前，人们开始研究Hom李色代数和Hom-δ-Jordan李色代数[9-12].本文构造了Hom-δ-Jordan李色代数，并研究了Hom-δ-Jordan李色代数的交换扩张.

定义1[4]设G是交换群，F是任意域.若∀a，b，c∈G，G上的一个映射ε：G×G→F*满足

ε(a，b)ε(b，a)=1，

ε(a，b+c)=ε(a，b)ε(a，c)，

ε(a+c，b)=ε(a，b)ε(c，b)，

则称ε为G的斜对称双特征标.易知

ε(a，0)=ε(0，a)=1，ε(a，a)=±1，∀a∈G.

设a，b，c为G-阶化向量空间中的齐次元，用|a|，|b|，|c|分别表示其次数.为简便，可用ε(a，b)表示ε(|a|，|b|).

定义2[10]Hom-δ-Jordan李色代数(L，[·，·]L，α，δ)由阶化空间L、双线性运算[·，·]L：L×L→L和偶的线性变换α：L→L构成，且满足：

[x，y]=-δε(x，y)[y，x]，δ=±1；

(1)

ε(z，x)[α(x)，[y，z]]+ε(x，y)[α(y)，[z，x]]+ε(y，z)[α(z)，[x，y]]=0，∀x，y，z∈L.

(2)

定义3 设(L，[·，·]L，α，δ)是Hom-δ-Jordan李色代数.

(1) Hom-δ-Jordan李色代数被称为保积的，若α为同态，即任取x，y∈L，均有α([x，y]L)=[α(x)，α(y)]L；被称为正则的，若α为自同构.

(2) 阶化子空间η⊆L称为(L，[·，·]L，α，δ)的Hom子代数，若α(η)⊆η且[x，y]L∈η，∀x，y∈η.

(3) 阶化子空间η⊆L称为(L，[·，·]L，α，δ)的Hom理想，若α(η)⊆η且[x，y]L∈η，∀x∈η，∀y∈L.特别地，理想η称为交换理想，若满足[L，η]=0.

定义4Hom-δ-Jordan李色代数(L，[·，·]L，α，δ)的表示，意指阶化向量空间V上关于A∈pl(V)的线性映射

ρA：L→pl(V)，

使得任意的u，v∈L满足

ρA([u，v]L)∘A=ρA(α(u))∘ρA(v)-δε(u，v)ρA(α(v))∘ρA(u).

(3)

2 Hom-δ-Jordan李色代数的构造

定义5 Hom-δ结合色代数(L，α，δ)由阶化空间L、双线性变换α：L→L构成，且其满足：

(λx)y=x(λy)=λ(xy)；

α(x)(yz)=δ(xy)α(z)，∀x，y，z∈L.

定理1 设(L，α，δ)是Hom-δ结合色代数，定义双线性映射[·，·]L：L×L→L满足[x，y]=xy-δε(x，y)yx，则(L，[·，·]L，α，δ)是Hom-δ-Jordan李色代数.

证明由于

ε(x，z)α(x)(yz)=δε(x，z)(xy)α(z)，

ε(x，y)ε(y，z)(zy)α(x)=δε(z，y)ε(x，y)α(z)(yx)，

ε(y，x)α(y)(zx)=δε(x，y)(yz)α(x)，

ε(y，z)ε(z，x)(xz)α(y)=δε(x，z)ε(y，z)α(x)(zy)，

ε(z，y)α(z)(xy)=δε(y，z)(zx)α(y)，

ε(z，x)ε(x，y)(yx)α(z)=δε(y，x)ε(z，x)α(y)(xz)，

可得

ε(x，z)[α(x)，[y，z]]+ε(y，x)[α(y)，[z，x]]+ε(z，y)[α(z)，[x，y]]=ε(x，z)[α(x)，yz-δε(y，z)zy]+ε(y，x)[α(y)，zx-δε(z，x)xz]+ε(z，y)[α(z)，xy-δε(x，y)yx]=ε(x，z)α(x)(yz)-δε(x，z)ε(x，y+z)(yz)α(x)-δε(x+y，z)α(x)(zy)+ε(x+z，y)(zy)α(x)+ε(y，x)α(y)(zx)-δε(y，z)(zx)α(y)-δε(y+z，x)α(y)(xz)+ε(y+x，z)(xz)α(y)+ε(z，y)α(z)(xy)-δε(z，x)(xy)α(z)-δε(z+x，y)α(z)(yx)+ε(z+y，x)(yx)α(z)=0.

定义6 设(T，[·，·]，α，δ)是Hom-δ-Jordan李色代数，(V，ρA，δ)为T-模，则线性映射ω：⊗2→V被称为2-上圈，若其满足下面等式：

ω(u0，u1)=-δε(u0，u1)ω(u1，u0)，

ε(f，μ0)ρA(α(u0))f(u1，u2)-δε(f+u0，u1)ρA(α(u1))f(u0，u2)+ε(f+u0+u1，u2)ρA(α(u2))f(u0，u1)-f([u0，u1]L，α(u2))+δε(u0+u1，u2)ε(u0，u2)f([u0，u2]L，α(u1))-ε(u0，u1)ε(u0+u1，u2)ε(u1，u2)f([u1，u2]L，α(u0))=0.

定理2 设ρA是保积Hom-δ-Jordan李色代数(T，[·，·]，α，δ)在V上的表示，这里V是由(T，[·，·]，α，δ)的全体线性变换构成的空间，线性映射ω：T×T→gl(V)满足ω([x，y]，α(z))=-ε(z，x+y)ω(α(z)，[x，y])，且ω(x，y)∘α=-ε(x，y)α∘ω(x，y).定义双线性运算：

[x+f，y+g]T⨁V=[x，y]+ω(x，y)-ε(x，y)g∘ρA(x)+δf∘ρA(y)，

α′(x+f)=α(x)+f∘α，∀x，y∈T，f，g∈gl(V).

则T⨁V关于定义的运算构成保积Hom-δ-Jordan李色代数，当且仅当ω为2-上圈.

证明首先验证(1)式成立.

-δε(x，y)[y+g，x+f]T⨁V= -δε(x，y)([y，x]+ω(y，x)-ε(x，y)f∘ρA(y)+δg∘ρA(x))= [x，y]+ω(x，y)-ε(x，y)g∘ρA(x)+δf∘ρA(y)=[x+f，y+g]T⨁V.

下面证明关于定义的运算满足(2)式，当且仅当ω为2-上圈.

事实上，

ε(x，z)[α′(x+f)，[y+g，z+h]]+ε(y，x)[α′(y+g)，[z+h，x+f]]+ε(z，y)[α′(z+h)，[x+f，y+g]]=0⟺

ε(x，z)ω(α(x)，[y，z])-ε(x，y)ω(y，z)∘ρA(α(x))+ε(y，x)ω(α(y)，[z，x])-ε(y，z)ω(z，x)∘ρA(α(y))+ε(z，y)ω(α(z)，[x，y])-ε(z，x)ω(x，y)∘ρA(α(z))+ε(y，x+z)h∘ρA(y)∘ρA(α(x))-δε(y，z)h∘ρA(x)∘ρA(α(y))+δε(z，y)h∘α∘ρA[x，y]+δε(x，z)f∘α∘ρA[y，z]+ε(z，x+y)f∘ρA(z)∘ρA(α(y))-δε(x，z)f∘ρA(y)∘ρA(α(z))-δε(x，y)g∘ρA(z)∘ρA(α(x))+δε(x，y)g∘α∘ρA[z，x]+ε(x，y+z)g∘ρA(x)∘ρA(α(z))=0⟺

-ε(x，y)ω([y，z]，α(x))+δε(z，x+y)ω([x，z]，α(y))-ε(x，z)ω([x，y]，α(z))+ε(x，z)ρA(α(x))∘ω(y，z)-δε(x，y+z)ρA(α(y))∘ω(x，z)+ε(y，z)ρA(α(z))∘ω(x，y)=0.

3 Hom-δ-Jordan李色代数的交换扩张

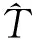
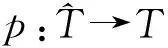
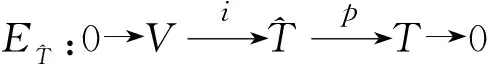
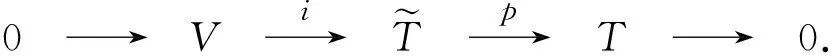
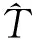
定理3 如上记号，则有(V，αV，θ，δ)是(T，α，δ)的表示，且不依赖于σ的选取.进而，等价交换扩张给出相同的表示.

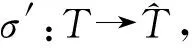
p(σ(xi)-σ′(xi))=xi-xi=0⟹σ(xi)-σ′(xi)∈Vσ′(xi)=σ(xi)+ui，

其中ui∈V.

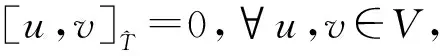
这表明θ不依赖σ的选取.

其次，证明(V，αV，θ，δ)是(T，α，δ)的表示.

通过计算可知，

αV(θ(x))(v)=δαV[σ(x)，v]=δ[αV(σ(x))，αV(v)]=δ[σ(α(x))，αV(v)]=θ(α(x))αV(v).

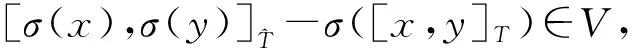
θ([x，y])∘αV(v)=δ[σ[x，y]，αV(v)]=δ[[σ(x)，σ(y)]，αV(v)]，

且

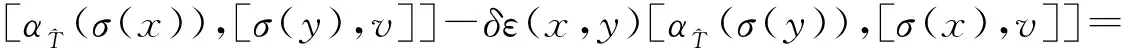
进而，得到(3)式成立.于是，可知(V，αV，θ，δ)是(T，α，δ)的表示.

最后，证明等价交换扩张具有相同的表示θ.