预加热效果对磁化套筒惯性聚变放能影响的模拟研究

赵海龙，王 强，阚明先，谢 龙

（中国工程物理研究院流体物理研究所，四川 绵阳 621999）

可控核聚变是解决未来能源需求的重要手段之一。当前传统的聚变构型如磁约束聚变（Magnetic confinement fusion,MCF）[1–3]和惯性约束聚变[4–6]（Inertial confinement fusion,ICF）等都面临着不同的工程和技术问题，距离点火的目标仍有一定的差距，因此有必要探索新的聚变构型方式，以尽量降低聚变的实现难度。

美国圣地亚国家实验室提出了一种结合传统MCF与ICF优势的新型聚变构型[7]——磁化套筒惯性聚变（Magnetized liner inertial fusion,MagLIF），其主要原理是利用大电流驱动金属套筒产生的超高压力（约16 TPa），压缩磁化并预加热燃料，使之达到聚变点火条件。该构型的最大优势在于使用外部热源（如激光器）对燃料进行预加热，使之完全等离子体化[8]，由此将轴向磁场冻结于燃料内，随着套筒内爆和燃料一起被压缩，可以显著抑制燃料热传导损失，提升α 粒子的能量沉积效率[9]，理论上能有效降低聚变实现的难度，具有极大的应用潜力。

关于MagLIF，理论、模拟以及实验研究均取得了快速进展[10–15]，并成功在Z 装置上进行了首批次氘燃料出中子实验[14]，然而实验得到的中子产额不如预期，有证据表明主要原因在于激光预加热模式下能量沉积效率过低，至此研究热点转向激光与等离子体的相互作用（Laser plasma interaction,LPI）[16–19]、激光预加热的替代方案[20]等，以便尽可能地提高预加热效率。

上述研究过于重视激光能量沉积效率的提升，而忽略了预加热自身参数对MagLIF过程和内爆结果的影响。为系统性地探究此问题，本研究将忽略LPI的复杂过程和能量沉积效率等问题，从预加热完成后达到的效果出发，使用一维集成化数值模拟程序（Magnetic implosion simulation tools，MIST）[21]开展预加热效果对MagLIF聚变放能的影响研究，基于参数扫描的方法，从简单模型着手，逐步深入探讨不同的预加热参数对内爆结果的影响。

1 计算模型与预加热必要性

首先建立MagLIF物理模型。对于磁化套筒惯性约束聚变而言，发生聚变时刻燃料处于高温（5～10 keV）、高密度（约1020cm−3）状态，可视为全电离、理想导电流体，驱动源来自外部电流，同时存在轴向磁场，整体上使用磁流体动力学（Magnetohydrodynamic，MHD）方程组描述是合适的。考虑到MagLIF包含了非常复杂的多物理过程，为便于一体化的描述，必须适当简化：

（1）认为氘氚（DT）燃料为完全电离的等离子体，燃料光性薄，金属套筒光性厚；

（2）经估算，典型参数下聚变反应导致的燃料质量减少不超过1%，因此不考虑聚变质量损失；

（3）根据模拟与实验结果[12,14]，在预加热后很短的时间（约20 ns）内电子和离子温度快速平衡，滞止时刻电子与离子温度差别很小，因此使用单温模型。

基于上述考虑，使用拉氏描述方式，建立描述MagLIF过程的单温、单流体、多介质MHD方程组

求解MHD方程组时需要材料状态方程的支撑，特别是对应的电导率和热导率参数。对金属套筒而言，电导率模型使用改进后的Burgess模型[23]；对于DT 燃料而言，则使用Zollweg 等[24]基于Spitzer 电导率模型改进的Z&L 模型，写作

式中：Z为离子平均电荷数，T为等离子体温度，γE为电子间碰撞对电导率的修正系数， Λm为修正后的库伦对数。对于1∶1混合的DT气体，Z= 1，γE=0.582。

式中：λD=68.66(T/ne)1/2[m]， λ+=0.62n−+1/3[m]，b0=5.6×10−6T−1[m]，其中ne为电子数密度，n+为离子数密度。

轴向强磁场的引入会影响燃料中电子和离子沿径向的热扩散，根据文献[22]，磁场影响下径向热扩散系数（高斯制）如下

式中：c0为真空中的光速；me为电子质量；mi=2.5mp为1∶1混合DT燃料的等效离子质量；Le、Li分别为电子和离子的库伦对数，聚变条件下DT 燃料密度约为1 g/cm3，温度约10 keV，此时Le、Li分别取7和9[22]；eg为高斯制下的电子电荷；Bg为高斯制下的磁场强度。

采用上述模型，自主编写了一维集成化数值模拟程序MIST，由此开展预加热方式的影响研究。MagLIF激光注入后与燃料的相互作用过程包含逆轫致辐射、受激布里渊散射、拉曼散射等非常复杂的作用机理，而本研究的主要目标并非探究激光在等离子体中沉积的具体过程和微观机理，只关注预加热后不同的燃料参数对内爆结果的影响，因此从简化问题出发，假设所有预加热能量均100%被燃料吸收。

首先通过计算，对比讨论预加热的必要性问题。以ZR 装置的驱动能力为出发点，考虑如下较典型的MagLIF负载参数模型：金属铍（Be）套筒，驱动电流峰值27 MA，上升时间约120 ns（如图1所示，来自文献[7]中ZR 装置95 kV 充电电压下的电流曲线），套筒外半径0.3 cm，位型比（套筒半径与厚度的比值）为6，高度1 cm，燃料为1∶1混合DT，燃料半径为0.25 cm，初始密度为3 mg/cm3，初始轴向磁场Bz为30 T，在套筒即将向内压缩时刻通过对燃料温度赋值的方式进行平均加热，预加热温度为250 eV，网格数60，空间分辨率50µm。为更加清晰地获得激光预加热本身的影响，暂不考虑端面损失和Nernst 效应，计算结果如图2所示。

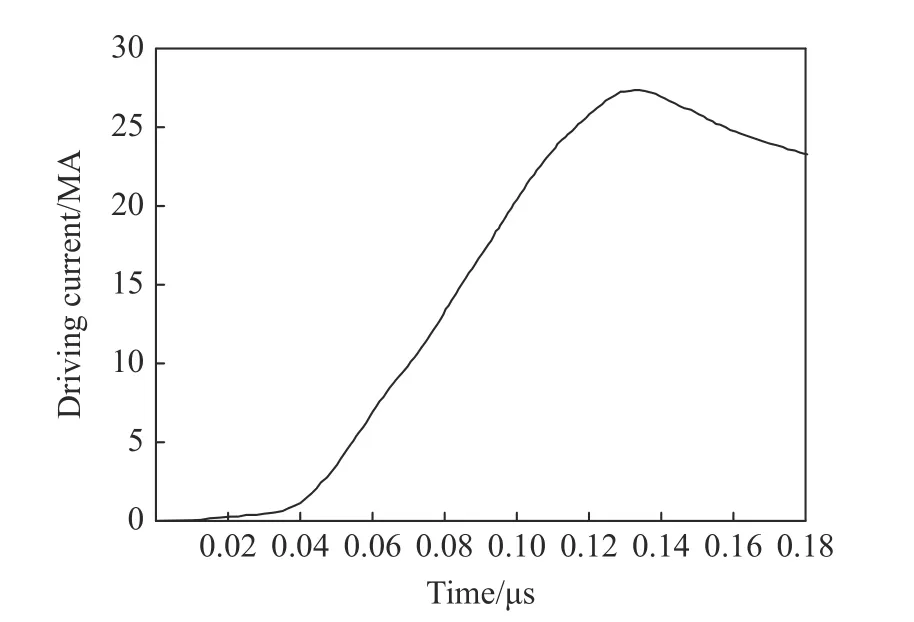
图1 ZR 装置在95 kV 充电电压下的驱动电流随时间演化曲线[7]Fig.1 Driving current from ZR facility with charging voltage95 kV[7]

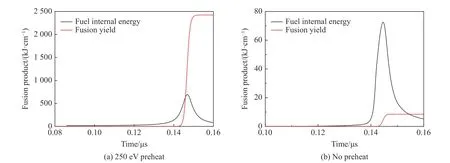
图2 250 eV 预加热温度与无预加热条件下计算得到的燃料内能和聚变产额随时间演化曲线Fig.2 Demonstrations of fusion yield and fuel internal energy calculated with 250 eV and no preheat

图2分别显示了预加热温度为250 eV 和没有预加热情况下，由相同初始参数计算得到的燃料内能和聚变产额随时间演化曲线。从图2（a）可以看出：250 eV 预加热情况下，聚变产额为2420 kJ/cm，内能峰值约700 kJ/cm，定义燃料能量增益Q为聚变产额除以峰值内能，则Q=3.5，说明聚变反应较成功。从图2（b）可以看出，在没有预加热的情况下，聚变产额仅为8.5 kJ/cm，尚不及燃料峰值内能的1/8，说明该条件下燃料未能充分发生聚变反应并释放能量；而且，此时整个燃料的压缩比高达56，如此高的压缩比对套筒界面稳定性的维持是极大的挑战。对比两种计算结果可以看出，对燃料进行预加热是MagLIF构型能够成功的必要条件。

2 预加热的影响与优化

预加热过程涉及诸多影响因素。首先考虑预加热时刻的选择，从物理过程上分析：如果加载时间过早，会增加端面效应引起的燃料质量损失、温度降低；加载过晚，则不能最大程度地利用套筒驱动能力、提升压缩效率，且套筒将轴向磁场压缩得更高，过于抑制径向热传导，导致轴心区域温度很高，却无法向外传递，大量外围燃料处于冷态。因此，最佳时刻应为套筒即将开始向内压缩时刻。考虑端面损失效应后的计算结果验证了上述观点，在此不做详细展示。

2.1 预加热温度优化

预加热温度的高低决定了初始加热效果，其本质上是对外部热源的能量需求。为简化问题，认为燃料在套筒即将内爆时刻（约86 ns）被瞬间、均匀地加热。保持第1节模型中其他参数不变，对预加热温度进行参数扫描，分别设定50、100、150、200、250、300和350 eV 7个预加热温度进行计算，得到所需的预加热能量、轴心处燃料峰值温度、燃料峰值内能、聚变产额及能量增益Q等参数，结果如表1 所示。

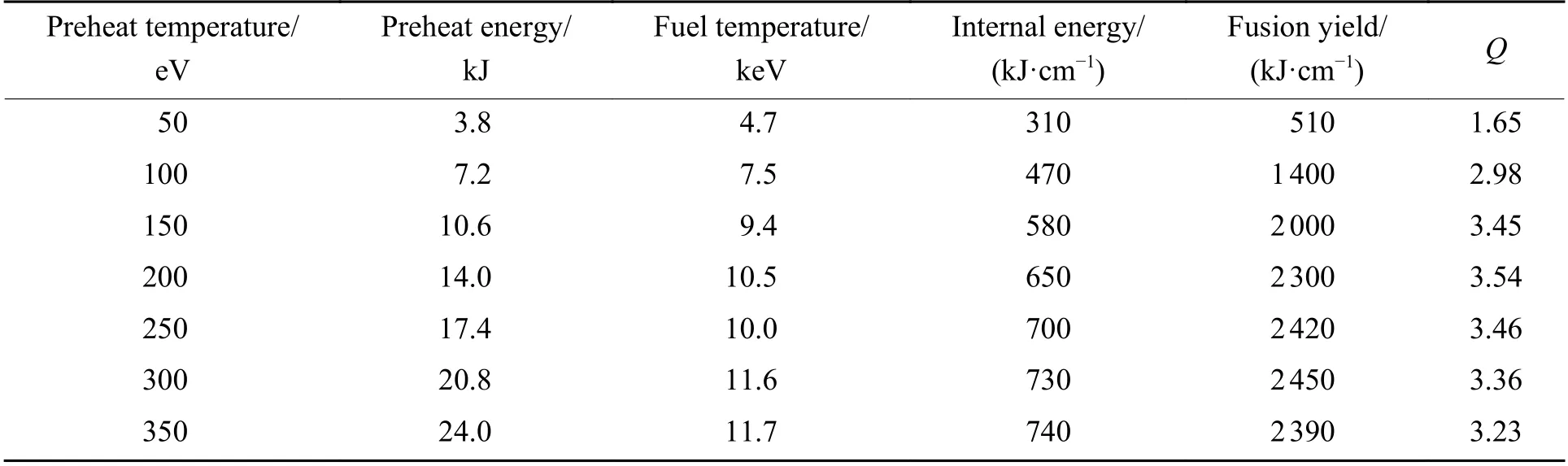
表1 不同预加热温度下计算得到的内爆结果对比Table 1 Calculated implosion resultswith different preheat temperatures

根据表1的结果，预加热温度在50～200 eV 区间时，燃料峰值内能和聚变产额均随预加热温度的升高呈快速上升趋势，其中聚变产额的上升速度更快，超过200 eV 后，二者的上升速度变缓，甚至随着预加热温度的继续升高（大于300 eV），聚变产额开始下降，如图3（a）所示。这是因为预加热温度需要综合考虑负载几何参数、燃料成分、密度、驱动能力等因素，就本算例而言，高于300 eV 的预加热温度会使燃料在迟滞状态时超出套筒的约束能力，有效聚变反应时间减少，导致聚变产额开始降低。

如果以聚变产额的大小作为判断依据，那么对于本研究以ZR 装置驱动能力为目标的算例而言，初始预加热温度为300 eV 时最佳，产额最高达2450 kJ/cm。但是，从图3（a）可以看出，此时聚变产额已进入平台区域，与预加热温度为200、250和350 eV 时的计算结果差别不大，而对应所需的预加热能量则相差很多（14～24 kJ，受限于建模和计算能力，此处未考虑辐射场）。若综合考虑燃料的能量增益Q，则初始预加热温度为200 eV 时，效果最好，能量增益最大（Q=3.54），如图3（b）所示，该参数下所需的预加热能量仅为14 kJ，聚变产额可达2300 kJ/cm，与最高值相差不大（约5%）。

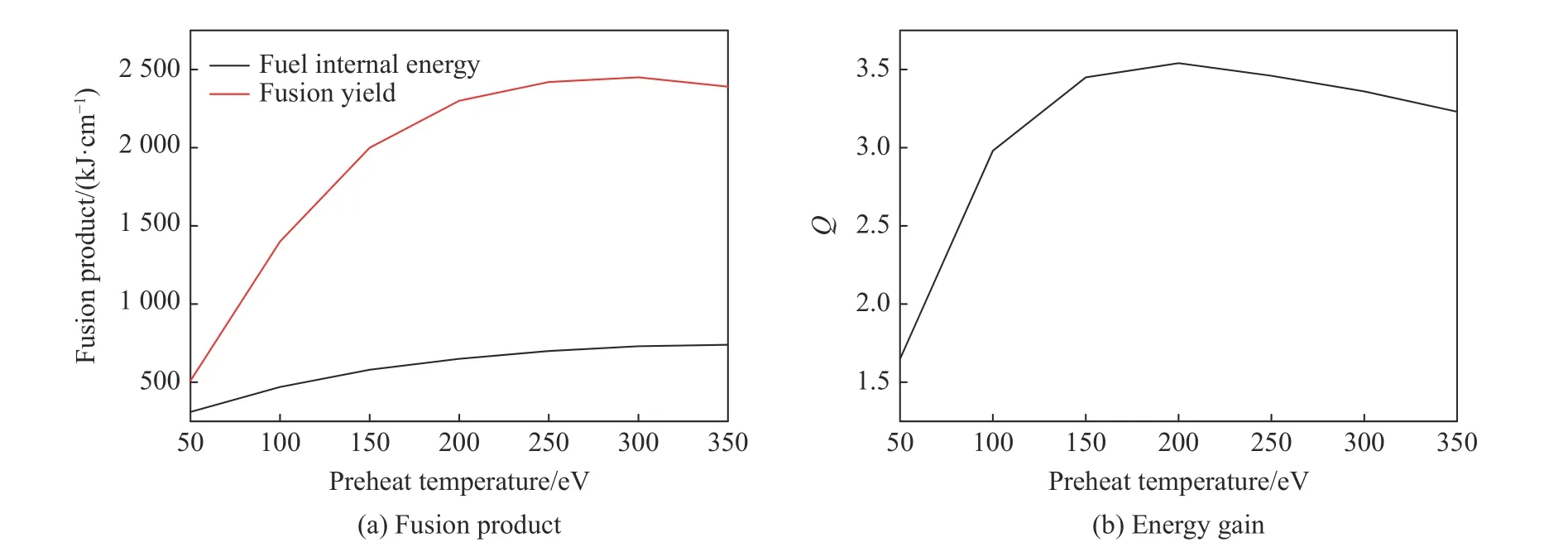
图3 不同初始预加热温度下计算得到的内爆结果对比Fig.3 Demonstrations of implosion results calculated with different preheat temperature

2.2 能量径向分布影响

均匀、瞬态的预加热是便于简化和分析问题的理想情况，与实际情况有所差别。首先预加热需要经历一定的过程才能完成（激光加载过程约2 ns），其次加热后燃料中的温度分布也不可能是均匀的，因此本研究采用余弦函数描述燃料中各个格点所得到的能量径向分布

式中：Ei（x）为第i个格点分得的能量，E0为轴心处格点分得的能量，Ri（x）代表第i个格点的位置，Rf为燃料初始半径。上述余弦函数的设计形式既能尽量模仿激光加热的实际效果，也能保证在套筒与燃料交界面处自然截断。对式（12）沿径向积分，积分结果等于总的预加热能量，据此可以确定E0的取值。

保持第1节计算模型中其他参数不变，将预加热方式改为余弦分布，预加热能量为14 kJ，在1 ns内沉积到半径为0.25 cm 的DT 燃料中，计算得到滞止时刻燃料温度和密度沿径向分布，如图4所示。可以看出，燃料轴心处温度很高（近18 keV），周围燃料温度则显著低于轴心。相应的密度分布则恰好相反，总体上形成一个中间热但密度低、周围冷但密度高的中空结构（Hollow structure），对聚变反应并不有利。相应的内爆结果如图5所示。该方式下最终聚变产额为2260 kJ/cm，峰值燃料内能为650 kJ/cm，均低于均匀加热情形下的内爆结果。

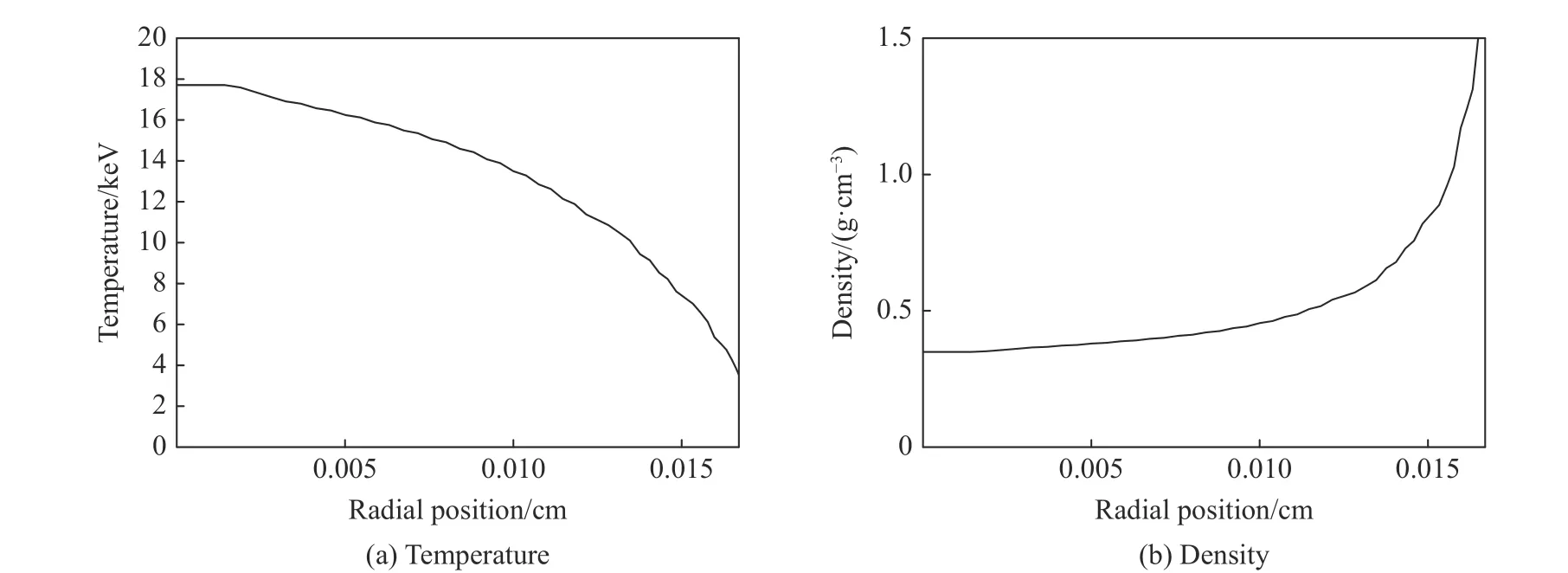
图4 余弦预加热方式计算得到的滞止时刻燃料温度和密度分布曲线Fig. 4 Distributions of fuel temperature and density at stagnation time with cosine preheat

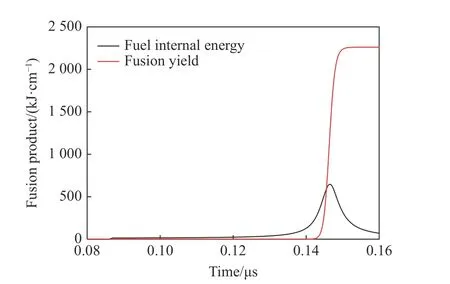
图5 余弦预加热方式计算得到的聚变产额与燃料内能演化曲线Fig.5 Demonstrations of fusion product and internal energy calculated with cosine preheat

上述计算中预加热范围均为所有燃料区域，下面将考虑更集中地利用能量对部分燃料进行预加热的情形。从学术探讨的角度出发，在余弦加热的基础上，分别以能量沉积半径（rLEH）为0.20、0.15和0.10 cm 注入14 kJ 能量，保持其他计算参数不变，分别计算得到预加热时刻（87 ns）和迟滞阶段温度分布曲线，如图6所示。

从图6可以看出，将能量集中沉积于部分燃料区域后，轴心附近的预加热温度显著提高，在能量沉积半径为0.20、0.15和0.10 cm 3种情况下分别增加到0.71、1.25和2.75 keV；然而，迟滞阶段再次出现前面所述的中空结构，且沿径向的燃料温度分布曲线极不光滑。沉积半径为0.2 cm 时，整个计算过程尚可完成，得到滞止时刻为146.1 ns时燃料温度的分布，轴心处燃料温度约30 keV；而沉积半径为0.15和0.10 cm 两种情况下，由于轴心处温度过高，超过列表式状态方程库的上限（约35 keV），导致计算过程无法完成，图6（b）展示了计算最后时刻燃料中相应的温度分布。

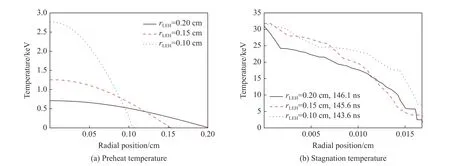
图6 不同沉积半径下预加热和迟滞阶段的温度分布曲线Fig.6 Distributions of preheat and stagnation temperatures with different preheat radius

沉积半径为0.20 cm 时，得到的聚变产额为2120 kJ/cm，燃料峰值内能为630 kJ/cm，均小于完全加热（沉积半径0.25 cm）的计算结果，说明燃料的预加热温度梯度对内爆结果有很大影响，应尽量减小径向温度差异。

由于轴向磁场压缩后对径向热扩散有较明显的抑制作用，为进一步验证中心加热方式是否有优势，尽量降低轴向磁场的影响，将初始轴向磁场强度Bz由30 T降低至5 T，分别采用0.25、0.20、0.15和0.10 cm 4种沉积半径，将14 kJ 的能量通过余弦分布方式注入燃料中，保持模型其他参数不变，计算得到的迟滞阶段温度分布和聚变产额如图7所示。

从图7（a）可以看出，降低轴向磁场对于温度分布的改善有限，迟滞阶段燃料中温度沿径向的梯度依旧很大，且沉积半径为0.10和0.15 cm 两种情况下依旧无法完成计算，温度上限超出状态方程数据库范围。此外，轴向磁场的降低同时影响了聚变产物α 粒子的能量沉积效率，以沉积半径0.25 cm 为例，计算得到的聚变产额仅有1950 kJ/cm，相比Bz= 30 T时显著降低，如图7（b）所示。上述温度分布图中出现了一定程度的不连续点，这主要是由于聚变反应时刻的温度沿径向分布梯度很大，现有的网格精度（60 个）不够高，导致部分区域（如轴心附近）相邻网格点的温度差距较大。

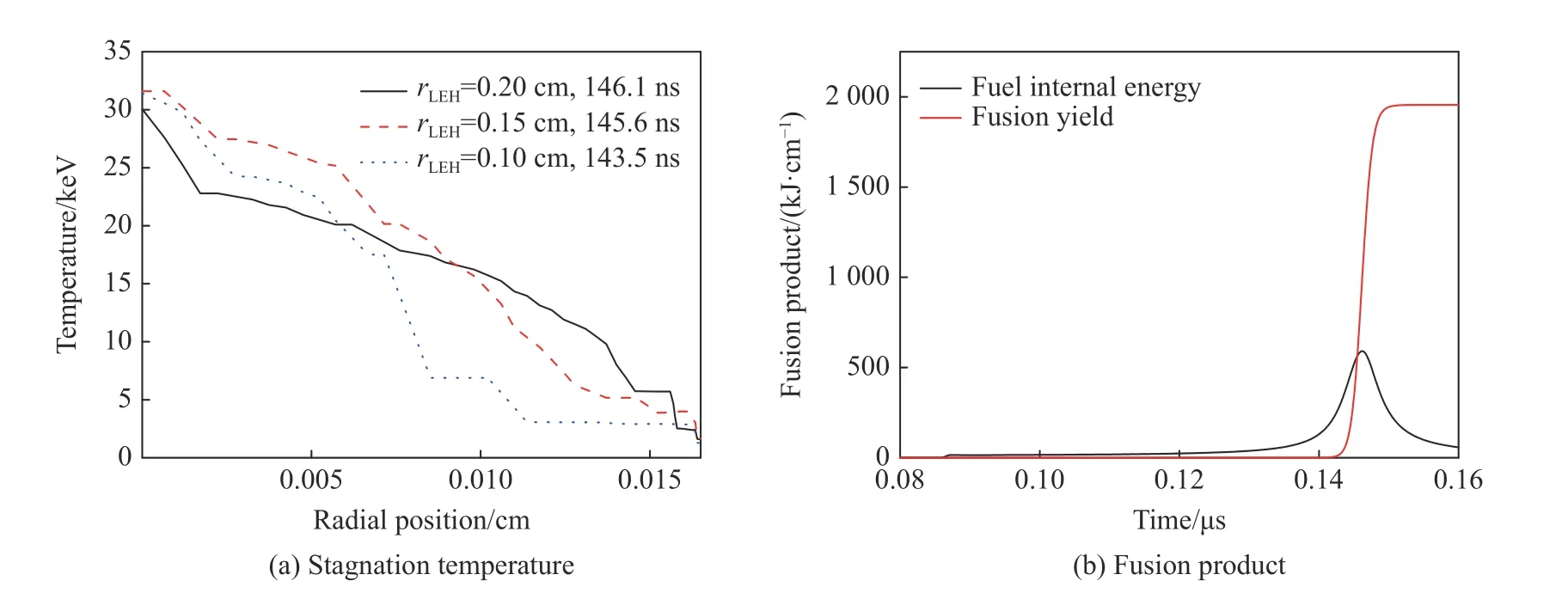
图7 不同沉积半径下迟滞阶段的温度分布和聚变产额演化曲线（Bz = 5 T）Fig. 7 Distributionsof stagnation temperatureand evolvement of fusion product with different preheat radii (Bz = 5 T)

上述算例均采用了较高的预加热温度，为进一步确认中心局部加热的结果，评估激光能量大小的影响，将预加热能量降低到现有激光器可达到的水平，使用3 kJ 的能量（Elas，神光Ⅲ原型激光装置的最大单束输出能量[25]）通过余弦分布方式注入燃料中，初始轴向磁场仍为5 T，分别采用0.25、0.20、0.15和0.10 cm 4种沉积半径，保持其他计算参数不变。4个算例都能够完成计算，计算得到的聚变产额分别是644、893、957和876 kJ/cm，其中沉积半径为0.15 cm 时得到的产额最高，绘制的预加热时刻温度分布和燃料轴心位置温度随时间演化曲线如图8所示。

图8 不同沉积半径下预加热时刻和迟滞阶段温度分布（Bz = 5 T, E las = 3 kJ）Fig.8 Distributionsof preheat and stagnation temperature with different preheat radii(Bz = 5 T, E las = 3 kJ)

从图8中可以看出：4种沉积半径下3 kJ 的能量分别将燃料轴心处的温度加热到92、148、265和600 eV；随着套筒的不断压缩，滞止时刻轴心处燃料温度升高至8.9、15.8、20.0和28.5 keV，显著高于Bz=30 T、Elas=14 kJ 的计算结果，可见轴心区域的燃料被压缩得更紧了，然而相应的聚变产额却远低于后者。两种情况的最大差别在于聚变状态不同，在Bz=30 T、Elas=14 kJ 情况下滞止时刻各算例的燃料状态均远高于磁化靶点火判据[22]，而在Bz=5 T、Elas=3 kJ 情况下虽然燃料峰值温度很高，但磁化强度BR却均未达到点火状态，这点在图9中有清晰的展示。

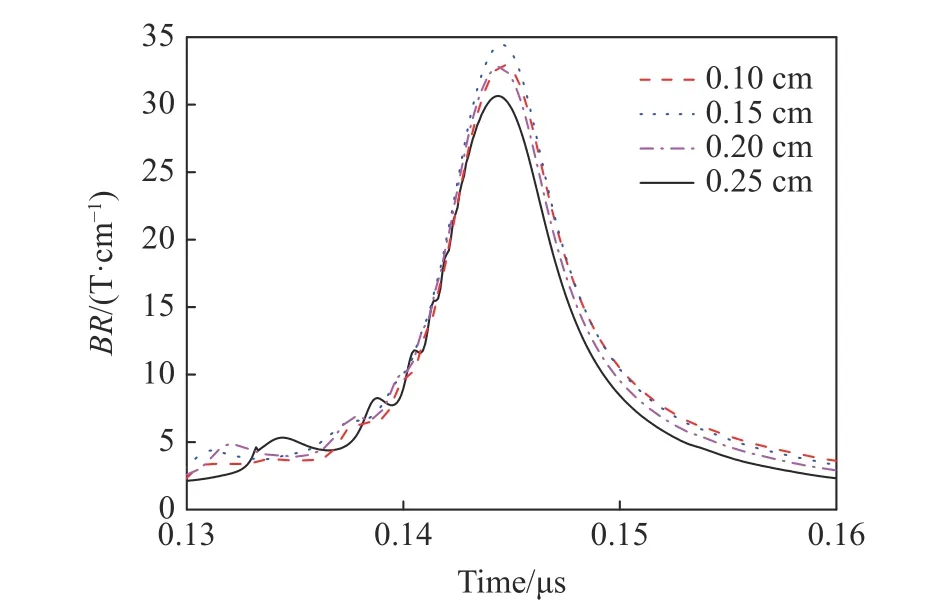
图 9 不同沉积半径下磁化强度BR随时间演化曲线(Bz = 5 T, E las = 3 kJ)Fig.9 Schematic of BR evolving with time with different preheat radii (Bz =5 T, E las= 3 kJ)

综上所述，预加热所需的能量与分布受多种条件的制约，需要根据负载几何参数、燃料密度、驱动能力等多种因素来确定。总的设计原则：通过预加热阶段，让燃料获得较高温度的同时，尽量使温度沿径向分布的梯度越平缓越好。在本研究的现有物理模型下，当滞止时刻聚变状态超过点火判据时，中心局部加热方式不如整体加热有优势；反之，当滞止时刻聚变状态未达到点火时，则中心局部加热更有优势。中心局部加热方式对于暂时不具备大能量激光器的实验构型设计非常有帮助，然而加热半径设计需要谨慎，能量过于集中时，容易导致激光穿透燃料而烧蚀电极材料。

2.3 注入功率和脉宽影响

进一步考虑在给定能量（如14 kJ）的前提下能量的脉冲宽度和功率参数对内爆结果的影响。假设采用激光作为预加热模式，其功率随时间演化呈标准的矩形方波，上升沿和下降沿均为0.1 ns，总能量固定为14 kJ 不变，以86 ns为中心，分别考虑脉宽为1、2、5和10 ns的情况，对应的功率分别为14.0、7.0、2.8和1.4 MJ/µs，功率曲线如图10所示。保持模型中其他计算参数不变，开展对比计算。

图10 不同脉宽时预加热功率曲线Fig.10 Schematic of preheat power with different durations

4种条件下，计算得到预加热结束时燃料温度分布如图11所示。在脉宽为1、2、5和10 ns的条件下：轴心处最高温度分别达到450、442、430和414 eV，拉长脉宽（如5、10 ns）时预加热后温度的径向梯度有了明显改善；相应的聚变产额分别为2259、2248、2244和2230 kJ/cm，与2.2节得到的温度梯度越平缓越好的结论不一致。其原因在于，当脉宽过长时（如10 ns），随着燃料中心温度持续升高并向外膨胀，套筒却向内不断压缩，双重作用下外层燃料的密度被压得很高，相应的温度却没有显著提升，部分燃料内能因膨胀做功而损失掉，这点从预加热结束时燃料获得的内能（分别为143.5、141.0、136.5和134.2 kJ/cm）可以看出，因此聚变产额才随着脉宽拉长而降低。基于上述结果，可以认为激光预加热模式中，激光的脉宽越短越好，从而避免因部分燃料持续升温向外膨胀而导致总的燃料内能降低。

图11 不同激光脉宽和功率参数下预加热时燃料中温度和密度分布Fig.11 Distributions of fuel temperature and density with different laser power and durations at preheat time

2.4 套筒高度的影响

套筒高度这一参数很重要，在保持其他参数不变的情况下，套筒高度的变化会直接影响以下参数及过程：负载电感、燃料预加热温度、端面质量损失、套筒RT不稳定性。较长的套筒有利于降低端面效应带来的质量损失，但是会增大负载电感和质量，从而降低加载电流，并导致驱动能力弱化，同时还会影响预加热效果；较短的套筒则可能导致激光在燃料中无法充分沉积，容易烧蚀电极表面引入混杂，并加剧端面损失，另外对加工和装配精度的要求也更高。一维MIST程序无法考虑套筒RT不稳定性带来的影响，因此该影响因素不予讨论，此外端面损失超出了本研究范围，将在后续研究中深入讨论。

要讨论负载高度的影响，首先需建立Z装置和ZR 装置的简化等效电路模型[26–27]，如图12所示，其中：Voc为装置绝缘堆处的驱动电压，一般由实验测量给出波形曲线；Z0为驱动器的等效电阻，约0.15Ω；L为磁绝缘传输线的等效电感，L0为汇流区结构和内磁绝缘传输线的等效电感，两者之和约为10.6 nH；Rloss为由汇流区空间电子流等引起的阻性（Resistive）电流损失项，与本计算的相关度不高，在此予以忽略；Ltarget为负载动态阻抗变化。Ltarget由下式给出

图 12 简化后的ZR 装置的等效电路示意图[25]Fig.12 Schematic of simplified equivalent circuit of ZR facility[25]

式中：h为套筒高度，R1和R2分别为初始时刻与当前时刻的套筒半径。

提取文献[27]中的数据，可以获得ZR 装置绝缘堆处的输出电压，如图13（a）所示。采用前文基准负载参数计算得到的电流曲线如图13（b）所示，峰值电流约26.5 MA，上升时间约120 ns，后续计算均使用该电路参数作为输入条件。

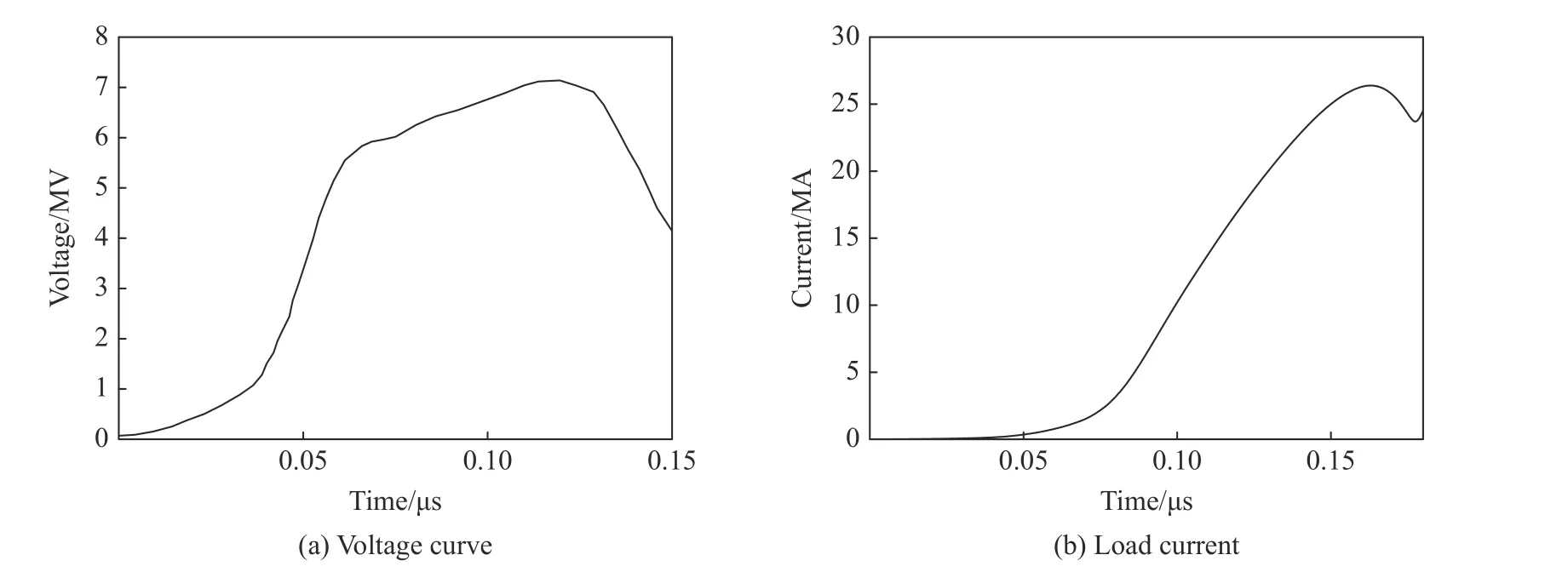
图13 ZR 装置绝缘堆电压曲线和MIST 程序计算得到的负载电流曲线Fig.13 Voltage curvefrom the vacuum insulator and calculated current curve by MIST code

采用上述电路模型和参数代替原有电流曲线的输入方式，并保持其他负载参数及预加热能量14 kJ、脉宽2 ns（85～87 ns）不变，考虑套筒高度分别为0.50、0.75、1.00和1.25 cm 的情况，计算得到的内爆结果对比如表2所示。

表 2不同套筒高度计算得到的内爆结果对比Table 2 Calculated implosion results calculated with different liner heights

从表2中可以看出，随着套筒高度的增加，预加热温度、峰值电流、单位高度的燃料内能和聚变产额等主要参数均呈单调下降趋势。若以此为判据，则一维程序计算结果显示套筒高度越小越好，更有利于提升内爆效果；然而从总的聚变产额出发，对于本研究以ZR 驱动能力为目标的算例而言，套筒高度为1.0 cm 时得到的产额最大，达到1614 kJ，故1.0 cm 为最佳的负载设计高度。值得关注的是，在套筒高度为1.0 cm 的情况下计算得到的聚变产额相比第1节直接用电流曲线输入的结果要小得多，说明计算中所使用的负载参数与装置驱动能力不匹配，需要进一步优化设计。

3 总结与讨论

围绕MagLIF过程中预加热效果对聚变放能的影响问题进行了数值模拟研究。计算结果表明：预加热机制的存在是MagLIF构型能够成功聚变的必要条件，最佳时间是套筒在电流驱动下即将开始向内压缩燃料时刻；燃料预加热的设计原则是通过预加热阶段后让燃料获得较高温度的同时，尽量使温度沿径向的梯度越平缓越好；在本研究现有的物理模型下，当滞止时刻聚变状态超过点火判据时，采用中心局部燃料进行预加热的方式不如整体加热有优势，反之，当滞止时刻聚变状态未能达到点火时，则中心局部加热更有优势；脉宽越短越好，可避免部分燃料持续升温向外膨胀导致所获得的燃料内能降低；随着套筒高度的增加，预加热温度、峰值电流、燃料内能和聚变产额等主要参数均呈单调下降趋势，然而从总的聚变产额出发，对于本研究以ZR 驱动能力为目标的算例而言，套筒的最优高度为1.0 cm；实际操作中需要考虑激光能量沿轴向沉积对电极的烧蚀因素，以及不稳定性发展的影响等。

受计算条件和篇幅限制，本研究仍有不足之处，如计算中忽略了RT 不稳定性和端面损失效应的影响。其中，对于使用金属铍套筒的MagLIF典型负载参数而言，位型比（半径与厚度的比值）通常为6，较厚的套筒以及轴向磁场的引入都对RT不稳定性的发展有较大的抑制[28]，套筒内壁保持较好的一致性，因此在一维数值模拟中暂不考虑。端面效应与燃料加热是一枚硬币的两面，必然伴随着激光预加热而同时发生，本着科学的原则，将其分别进行独立探讨是有必要的，它将有助于我们更加专注预加热自身参数的影响。这些不足将在今后工作中逐步完善。