爆破振动下双洞隧道衬砌动力响应分析

凌同华，欧阳雄志，刘建伟，张胜

爆破振动下双洞隧道衬砌动力响应分析

凌同华1，欧阳雄志1，刘建伟1，张胜2

(1. 长沙理工大学 土木工程学院，湖南 长沙 410114；2. 湖南城市学院 土木工程学院，湖南 益阳 413000)

以浙江省金华市里岩垄坑2号隧道为工程背景，研究Ⅲ级围岩隧道爆破时衬砌动力响应。本文采用MinimateProTM振动监测仪对开挖洞与邻洞进行了爆破振动测量，并利用Midas GTS NX对双洞隧道进行数值模拟分析。研究结果表明：本洞初衬振动速度和位移的最大值发生在拱顶处，横向上的大小远小于纵向和竖向。对于纵向，拱顶及拱肩处的质点振动峰值速度远大于其他关键位置的，各关键位置的竖向位移和速度变化趋势相同，但仍是拱顶处最大；本洞初衬应力最大值位于拱腰处，先行洞应力最大值在左拱腰处；其速度与位移的最大值位于左拱肩；先行洞二衬与后行洞掌子面的纵向间距应为15～20 m。本文研究结果可为双洞隧道的爆破施工提供 指导。

隧道工程；动力响应；数值分析；爆破；隧道衬砌

中国隧道施工条件复杂，在设计理论和工程实践等方面遇到了诸多难题[1]。部分隧道工程受复杂的地质情况和地形条件、线路总体规划走向、工程预算等诸多因素影响，采用侧壁导坑、三台阶、上下台阶和全断面等不同方法进行开挖。钻爆法是山岭隧道运用最广的开挖手段。山岭隧道穿越坚硬围岩区域时，为保证隧道循环进尺长度，会采用较多药量保证爆破效果，但爆破施工造成爆源周围介质地强烈振动，对隧道衬砌结构造成损坏。因此，有必要对隧道衬砌结构进行隧道的爆破动力响应分析。国内外学者对比已进行了大量研究[2−7]。凌同华[8]等人采用现场试验与数值模拟相结合，获得了分岔隧道过渡段的振速研究及动力响应情况。胡守云[9]等人通过现场测试与数值模拟，讨论了隧道下穿机场跑道爆破施工对机场的影响。高杰[10]研究了常速、缓慢铁路列车行驶动载作用下隧道初期支护的应力和位移响应。仇文革[11]等人通过室内相似模型试验对深埋硬岩隧道初期支护的劣化过程进行了模拟。吴忠仕[12]等人通过三维数值模型，在应力位移方向对既有隧道进行动力响应分析。但在隧道爆破荷载作用下对隧道初期支护结构的动力响应研究较为少见。因此，本研究以浙江省金华市里岩垄坑2号隧道双洞隧道工程爆破为例，根据现场监测数据和数值模拟结果，拟分析后行洞及先行洞初次衬砌结构，得到关键位置处3个方向的质点振速、应力和位移的响应规律，并通过对先行洞衬砌振速的研究，得出先行洞最优二次衬砌施工位置。

1 工程概况

里岩垄坑2号隧道位于永康至武义公路改建工程内，全长864 m，洞身段埋深大，顶板最大埋深约为180 m。洞室岩性为中风化和微风化凝灰岩，岩芯较坚硬，岩质新鲜。在桩号ZK12+000处，采集现场爆破数据，并对该处进行数值模拟，观察爆破对后行洞与先行洞初期支护的动力响应。该隧道在Ⅲ级围岩处，采用上、下台阶分步开挖的形式。隧道宽为16.8 m，高为10.5 m。上台阶爆破如图1所示，炮孔深度为3～5 m，循环进尺为3 m，设计开挖方量286 m3，初衬采用15 cm厚C20喷射混 凝土。

图1 上台阶炮眼布置

隧道间距及测点布置如图2所示，其中，A为拱顶，B、C为拱肩，D、E为拱腰，F、G为拱脚，H为仰拱中点。

图2 隧道间距及测点布置(单位：m)

2 现场数据采集

表1 爆破振动监测数据

式中：为场地系数；为衰减系数。

对式(1)进行数学变换，左、右同时取ln可知：

由于v、R和Q为已知量，参数α和lnK分别为一元二次函数斜率及截距。因此，对各方向测试数值进行拟合，得出K、α的速度拟合曲线如图3所示。

从图3中可以看出，质点振动速度峰值在不同方向的传播规律为：

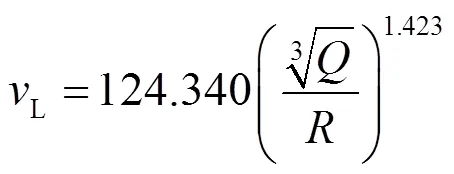
式中：T、V、L为横向、垂向、径向的质点振动速度峰值。

3 有限元数值模拟

选取部分Ⅲ级围岩进行模拟。由于模型的长和高为隧道最大宽度和长度的3倍以上，才能忽略模型边界对爆破振动的影响。因此，设置模型的长、宽和高分别为184 m、80 m和90 m。模型采用软件自动划分，尺寸控制由两侧到隧道中心，从4 m到1 m的网格。模型边界的顶部为自由边界，四周为无反射黏性边界，底部为固定边界，如图4所示。

图4 隧道3D模型

围岩和隧道支护结构中的动强度与静强度差别很大。王思敬[13]提出了围压衬砌结构静弹性模量(s)与动弹性模量(d)计算公式：

除了弹性模量，支护结构中泊松比同样存在动静之分，文献[14]提出两者之间的换算关系：

式中：d为动泊松比；s为静泊松比。

根据参考文献[13]和[14]中的取值，本模型材料的参数见表2。

表2 材料参数

注：为重度；为黏聚力；为内摩擦角

爆炸产生的冲击波沿径向均匀地作用在隧道洞壁上，三角形荷载作为爆破荷载。确定爆破荷载加卸载时长，本次试验加载时间[15]为10 ms，卸载时间为90 ms。爆破荷载作用在隧道洞壁上应力峰值可由式(8)计算得到[16]：

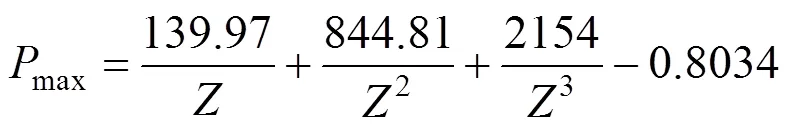
其中，的计算式为：

由于Ⅲ级围岩上台阶单段最大药量为59.1 kg，作用面的距离最不利长度约为1 m。由此，可求爆破荷载作用在洞壁上的应力峰值为140.705 MPa，得出该爆破荷载时程曲线如图5所示。

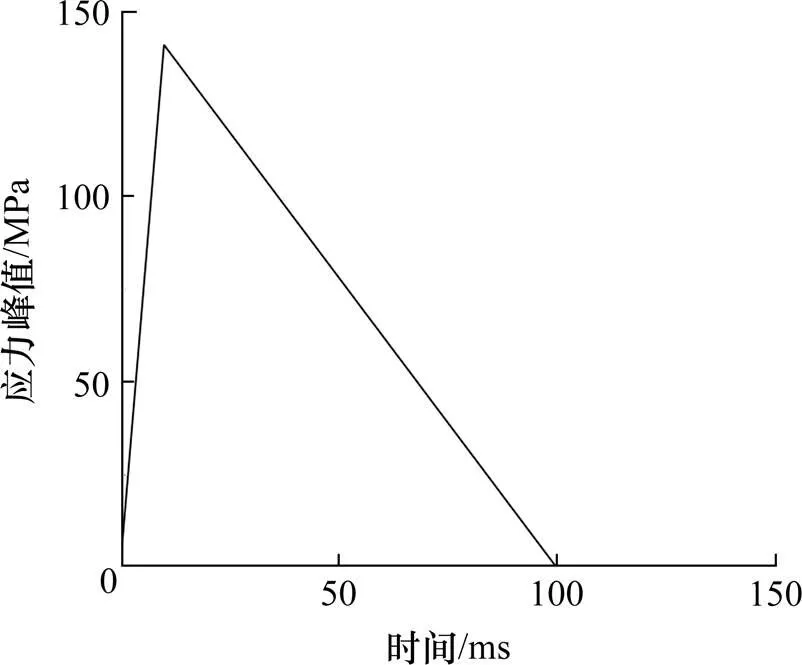
图5 爆破荷载时程曲线

4 动力响应分析

通过数值模拟，计算出掌子面前方40 m的拱腰处竖向质点峰值振动速度为2.79 cm/s。由表1中爆心距40.92 m处竖向峰值振动速度为2.92 cm/s和式(5)计算可知，后行洞的竖向质点峰值振动速度为3.71 cm/s。因数值模拟在均质围岩前提下进行，但实际工程围岩条件复杂，测试仪器也存在一定误差，从而导致数值模拟与现场仪器监测数据存在差异。虽然误差较小，但是仍能通过建立模拟对隧道衬砌的动力响应规律进行较好地反映。

通过对模型中后行洞距掌子面10 m处，以及先行洞距爆破位置最近隧道截面处的隧道拱顶、拱肩、拱腰、拱底及仰拱中点处，提取其各个方向上时程曲线，判断隧道爆破对后行洞隧道初衬影响规律和对先行洞衬砌动力响应规律。

4.1 后行洞隧道动力响应

4.1.1 衬砌振速响应

通过对模型进行动力响应计算，得出后行洞隧道爆破时程速度曲线，分别对横向、纵向和竖向3个方向进行分析，其结果如图6所示。

从图6中可以看出，对于后行洞隧道，横向上质点振动峰值速度在拱肩处最大，在拱顶处最小。纵向上，拱顶处的质点振动峰值速度最大，其次是拱肩位置。拱顶和拱肩位置的峰值速度远大于隧道同一断面其他监测位置的值，左右对称位置值一致。竖向上，同样拱顶处质点振动峰值速度最大，但隧道各监测点处变化趋势相同。

图6 后行洞速度时程曲线

4.1.2 衬砌位移响应

通过对模型进行动力响应计算，得出后行洞隧道爆破时程位移曲线，分别对横向、纵向和竖向3个方向进行分析，其结果如图7所示。

从图7中可以看出，对于隧道后行洞位移，横向上，拱肩、拱腰、拱脚的位移峰值依次变小，对拱顶和仰拱中点的影响不大。纵向上，拱顶位移最大，其次是拱肩和拱腰。由于上台阶爆破，拱脚和仰拱中点处位移沿反方向增长，拱顶处位移0.88 mm，为仰拱中点位移的3.5倍。竖向上，隧道拱顶处最大位移为1.42 mm，隧道各点竖向位移方向一致，均沿隧道轴线向上，位移大小随隧道从上至下逐渐减少。

图7 后行洞位移时程曲线

4.1.3 对隧道衬砌应力动力响应分析

通过对模型的后行洞与先行洞衬砌的最大主应力进行整理，见表3。表3中1代表先行洞衬砌最大主应力，2代表爆破后行洞衬砌最大主应力。

表3 隧道各位置最大主应力

由表3可知，隧道爆破时，后行洞衬砌应力最大值发生在拱腰处，其次是拱肩与拱顶。所以爆破过程中应重点监测隧道这3个关键部分的变化情况，确保隧道初衬不被损坏。先行洞应力最大值发生在左拱腰处，当隧道爆破后，也要注意爆破截面处先行洞处左拱腰以及左拱脚的变化情况。

4.2 对先行洞隧道动力响应

研究隧道爆破对先行洞衬砌的动力响应规律，能更好地找出各个方向上最危险处。然后对其进行分析，采取措施，从而保证先行洞隧道衬砌的安全，进而得出先行洞二衬的最优距离。

4.2.1 衬砌速度响应

通过对模型进行动力响应计算，得出先行洞隧道每个方向上爆破时程速度曲线，如图8所示。

从图8中可以看出，对于横向隧道先行洞，左拱腰处质点峰值速度最大，隧道上半部先到峰值，随后当隧道下半部到达峰值后，各处变化趋势相同。纵向隧道各点振动趋势大致相同，隧道左拱肩、左拱腰处的质点峰值速度相对较大，两者趋势都是隧道左部的峰值速度大于隧道右部的，而竖向上左拱肩峰值速度最大，拱顶的比左拱肩的略小。因此，重点监测先行洞左拱肩与拱腰处，能降低爆破对先行洞衬砌的影响。

4.2.2 衬砌位移响应

通过对模型进行动力响应计算，得出先行洞隧道每个方向上爆破时程位移曲线如图9所示。

从图9中可以看出，隧道爆破对先行洞衬砌位移的影响。隧道竖向的位移值为横向的3倍，纵向的位移相对于横向以及竖向的可忽略不计。因此，重点监测先行洞左拱肩处位移变化值，可保证先行洞隧道安全。

4.2.3 对先行洞二衬距离影响

依据《爆破安全规程(GB 6722−2014)》中规定的爆破振动安全允许标准，交通隧道中互相垂直的3个分量的安全允许振动速度范围为10～20 cm/s。《公路隧道施工技术细则(JTGT F60−2009)》中，隧道处于Ⅲ级围岩区段，间距略小于2倍隧道单洞的开挖面宽度，先行洞二衬的距离需满足爆破振动振速，不应大于10 cm/s，所以取最安全质点振动速度为10 cm/s。

由于2个隧道为平行关系，横向与纵向的最大安全距离分别取22.67 m、21.77 m，竖向取隧道净空高度的垂直距离10.6 m。由空间坐标轴3个方向矢量和可知，实际安全距离为33.17 m，相当于两条隧道之间直角三角形的斜边。而隧道间距30 m为其中一条直角边，先行洞二衬安全距离为另外一条直角边，距离为14.15 m。通过数值模拟，得出先行洞速度最大值均小于10 cm/s，即爆破不会对先行洞二衬造成影响。因此，对于先行洞二衬布置的间距，应该距后行洞掌子面15～20 m处进行布置，以保证安全及施工进度。

5 结论

通过数值模拟分析，隧道爆破施工对后行洞及先行洞的衬砌都会产生影响，得出结论：

1) 后行洞衬砌的振速响应在径向与竖向上影响较大，最大值发生在拱顶，其次为拱肩。衬砌的位移峰值在径向上，拱顶处位移2.69 mm，为仰拱中点的3.5倍。竖向拱顶上，位移最大值4.31 mm。施工过程中，加强拱顶处的支护强度，以及爆破后重点监视拱顶和拱肩变化情况，以保证隧道衬砌的稳定性。

2) 隧道爆破时，后行洞衬砌应力最大值发生在拱腰处，其次是拱肩和拱顶。爆破过程中，应重点监测隧道这3个部分的变化情况，以保证隧道初衬不被损坏。先行洞应力最大值发生在左拱腰处，当隧道爆破后，同样需注意先行洞处左拱腰以及左拱脚的变化情况。

3) 隧道爆破对先行洞衬砌位移的影响，隧道竖向的位移为横向的3倍，纵向位移与横向以及竖向位移相比，可忽略不计。因此，重点监测先行洞左拱肩处位移变化值，保证先行洞隧道安全。

4) 通过爆破振动安全允许标准及数值模拟数据相结合，得出先行洞二衬布置的间距应在距后行洞掌子面横截面15～20 m处进行布置是最经济实惠、安全的方案。

[1] 王梦恕.中国铁路、隧道与地下空间发展概况[J].隧道建设,2010,30(4):351−364.(WANG Meng-shu. An overview of development of railways, tunnels and underground works in China[J]. Tunnel Construction, 2010, 30(4): 351−364.(in Chinese))

[2] 李兴华,龙源,纪冲,等.爆破地震波作用下既有圆形隧道衬砌动应力集中系数分析[J].岩土力学,2013,34(8): 2218−2224.(LI Xing-hua,LONG Yuan,JI Chong,et al. Analysis of dynamic stress concentration factor for existing circular tunnel lining under blasting seismic wave[J]. Rock and Soil Mechanics, 2013, 34(8): 2218−2224.(in Chinese))

[3] 张胜,王智德,黎永索,等.基于模式自适应连续小波能量谱的爆破振动信号特征分析[J].爆破,2019,36(2): 105−110, 125. (ZHANG Sheng, WANG Zhi-de, LI Yong-suo, et al. Characteristics analysis of blast vibration signals based on pattern adapted continuous wavelet energy spectrum[J]. Blasting, 2019, 36(2): 105−110, 125. (in Chinese))

[4] 曹峰,凌同华,刘家澍,等.分岔隧道浅埋连拱段的爆破振动效应分析[J].公路交通科技,2018,35(2):86−94.(CAO Feng, LING Tong-hua, LIU Jia-shu, et al. Analysis on blasting vibration effect of shallow multi-arch section of bifurcated tunnel[J]. Journal of Highway and Transportation Research and Development, 2018, 35(2): 86−94.(in Chinese))

[5] 李磊,谭忠盛,喻渝,等.成兰铁路千枚岩隧道初期支护形式试验研究[J].土木工程学报,2017,50(S1):19−24.(LI Lei, TAN Zhong-sheng, YU Yu, et al. Experimental study on primary lining form of tunnels in phyllite on Chengdu-Lanzhou railway[J]. China Civil Engineering Journal,2017,50(S1):19−24.(in Chinese))

[6] 房倩,张顶立,王毅远,等.高速铁路隧道初支、二衬间接触压力研究[J].岩石力学与工程学报,2011,30(S2): 3377−3385.(Fang Qian, Zhang Ding-li, Wang Yi-yuan, et al. Study of contact pressure between primary lining and secondary lining for tunnels of passenger dedicated lines[J]. Chinese Journal of Rock Mechanics and Engineering,2011,30(S2):3377−3385.(in Chinese))

[7] 刘唐利,凌同华,陈增辉,等.爆破振动对既有隧道影响的数值模拟分析[J].交通科学与工程,2019,35(3):79−84. (LIU Tang-li, LING Tong-hua, CHEN Zeng-hui, et al. Numerical analysis of the effect of blasting vibration on existing tunnels[J]. Journal of Transport Science and Engineering,2019,35(3):79−84.(in Chinese))

[8] 凌同华,曹峰,张胜,等.分岔隧道过渡段的爆破振动特性研究[J].振动与冲击,2018,37(2):43−50.(LING Tong-hua, CAO Feng, ZHANG Sheng, et al. Blast vibration characteristics of transition segment of a branch tunnel[J]. Journal of Vibration and Shock, 2018, 37(2): 43−50. (in Chinese))

[9] 胡守云,周传波,蒋楠,等.P波作用下机场跑道的爆破安全振动速度研究[J].华南理工大学学报:自然科学版, 2018,46(4):129−136.(HU Shou-yun,ZHOU Chuan-bo, JIANG Nan, et al. Study on safety blasting vibration velocity for concrete airport runway subjected to P-waves[J].Journal of South China University of Technology:Natural Science Edition, 2018, 46(4): 129− 136.(in Chinese))

[10] 高杰.三孔小净距隧洞下穿既有铁路列车振动荷载动力响应研究[J].石家庄铁道大学学报:自然科学版,2016, 29(2):39−44.(GAO Jie. Dynamic response of three pipes small spacing tunnels under train-induced dynamic load[J]. Journal of Shijiazhuang Tiedao University: Natural Science Edition, 2016, 29(2): 39−44. (in Chinese))

[11] 仇文革,冯冀蒙,陈雪峰,等.深埋硬岩隧道初期支护劣化过程衬砌力学特性试验研究[J].岩石力学与工程学报, 2013,32(1):72−77.(QIU Wen-ge,FENG Ji-meng,CHEN Xue-feng, et al. Model testing research on lining mechanical variation with deterioration process of primary support in deep hard rock tunnel[J]. Chinese Journal of Rock Mechanics and Engineering,2013,32(1): 72−77.(in Chinese))

[12] 吴忠仕,陈培帅,王伟,等.扩建隧道爆破对既有衬砌的影响及安全判据[J].水利水电技术,2020,51(5):77−85.(WU Zhong-shi, CHEN Pei-shuai, WANG Wei, et al. Impact from blasting for tunnel expansion on existed tunnel lining and its safety criterion[J]. Water Resources and Hydropower Engineering,2020,51(5):77−85.(in Chinese))

[13] 王思敬,吴志勇,董万里,等.岩体工程地质力学问题(三)[M].北京:科学出版社,1980.(WANG Si-jing,WU Zhi-yong, DONG Wan-li,et al.Geomechanical problems of rock mass engineering (3)[M]. Beijing: Science Press,1980. (in Chinese))

[14] 戴俊.岩石动力学特性与爆破理论[M].北京:冶金工业出版社, 2002. (DAI Jun. Dynamic Behaviors and Blasting Theory of Rock[M]. Beijing: Metallurgical Industry Press, 2002. (in Chinese))

[15] 张彦辉,明华军.基于Midas/GTS的公路隧道爆破施工对地表高层建筑影响的研究[J].公路工程,2019,44(6): 171−176.(ZHANG Yan-hui, MING Hua-jun. Research on influence of highway tunnel blasting construction based on Midas/GTS on surface high-rise buildings[J]. Highway Engineering, 2019, 44(6): 171−176. (in Chinese))

[16] 刘国华,王振宇.爆破荷载作用下隧道的动态响应与抗爆分析[J].浙江大学学报:工学版,2004,38(2):204−209. (LIU Guo-hua, WANG Zhen-yu. Dynamic response and blast-resistance analysis of a tunnel subjected to blast loading[J].Journal of Zhejiang University:Engineering Science,2004,38(2):204−209.(in Chinese))

Dynamic response analysis of double tunnel lining under blasting vibration

LING Tong-hua1, OUYANG Xiong-zhi1, LIU Jian-wei1, ZHANG Sheng2

(1. School of Civil Engineering, Changsha University of Science & Technology, Changsha 410114, China;2. School of Civil Engineering, Hunan City University, Yiyang 413000, China)

Taking the No. 2 tunnel of Li yan long keng in Jinhua City, Zhejiang Province as the research object, the blasting dynamic response of lining in the grade III surrounding rock was investigated. The blasting vibration of the blasting tunnel and the adjacent tunnel was measured by the MinimateProTMvibration monitor. The numerical analysis of the double tunnel was carried out using Midas GTS NX. The results show that, the maximum value of vibration velocity and displacement of the blasting tunnel occurs at the vault, and the value in the transverse direction is smaller than that in the longitudinal and vertical direction. For the longitudinal direction, the peak particle velocity at the position of arch and shoulder is larger than that at the other key positions. The variation trend of vertical displacement and velocity of each key position is the same, and the value at the position of arch is maximum. The maximum stress of the primary support of tunnel is located at the arch waist. For the excavated tunnel, the maximum stress occurs at the left arch waist, the maximum velocity and displacement is located at the left arch shoulder. The longitudinal distance between the lining of the existed tunnel and the working face of the back tunnel should change from 15 m to 20 m. The results of this study can provide guidance for blasting construction of double-hole tunnels.

tunnel engineering; dynamic response; numerical analysis; blasting; lining

U455.6

A

1674 − 599X(2021)02 − 0020 − 08

2020−07−27

国家自然科学基金项目(51678071，51608183)；湖南省自然科学基金项目(2018JJ3022)

凌同华(1968−)，男，长沙理工大学教授，博士。