多换乘站多车场响应型接驳公交的协调优化

王顺，刘杰，姜宁宇，王正武

多换乘站多车场响应型接驳公交的协调优化

王顺1，刘杰2，姜宁宇2，王正武2

(1. 长沙市建设工程质量安全监督站，湖南 长沙 410016；2. 长沙理工大学 智能道路与车路协同湖南省重点实验室，湖南 长沙 410114)

为提高响应型接驳公交系统的运行效率，针对具有多个换乘站、多个车场的响应型接驳公交系统，提出了多换乘站多车场协同运营、车辆路径与调度协调设计的思路。同时考虑预约需求和实时需求，构建了响应型接驳公交多换乘站多车场地协同运行车辆路径与调度协调的二阶段模型，设计了多染色体遗传算法。计算结果表明：在给定的混合需求下，与独立运营相比，协同运营模式的总费用降低了14.4%，运行时间减少了24.2%，发车次数减少了3次；增加小车型占50%时，独立运营和协同运营的系统总费用分别降低了7.3%和7.5%。

两阶段法；多车场；多换乘站；响应型接驳公交

为解决城市边缘地区居民出行的“第一或最后一公里”问题。响应型接驳公交(responsive feeder transit，简称为RFT)受到了广泛的关注[1]。为完善城市的公交系统，推动RFT的实际应用，Guo[2]等人通过24 h的运营模拟验证了低需求量条件下RFT具有的优势。Edwards[3]等人采用客流数据确定了RFT的最佳运行时段。Frei[4]等人发现出行者选择地铁出行的同时也倾向于选择RFT。为更好地契合实际情况，Ghannadpour[5−6]等人提出了考虑多种约束的多目标模型和双层规划模型。Lu[7]等人以车辆总运行时间最小为目标，构建了可优化发出车辆数的调度模型。Chen[8]等人验证了RFT系统中径向网络的优势。Rahimi[9]等人根据经验数据与所构建连续模型的关系，求解了新泽西州公交系统的运行成本。随着研究的不断深入，不同的启发式算法也应用到模型的计算中[10−11]，并构建了混合需求下的运行线路优化模型[12]，同时探讨了分区协调运行模型、同时接送的线路优化模型、多换乘站的协调优化模型[13−15]。但现有研究均为关注车场单一且位于换乘站的情况，接驳车辆一般从运营公司的停车场出发，接送乘客，回到停车场。当系统服务范围较大时，为合理规划运行，路径车辆需分多个车场停放，现有研究很少考虑协调运营多个换乘站。因此，本研究拟以多个换乘站、多个车场的RFT系统为研究对象，考虑同时有预约需求与实时需求时，通过多换乘站多车场的协调运行、车辆路径与调度的协调优化，确定系统中所有车辆服务的换乘站、运行路径、发车时刻、发出车型、返回车场等，提高RFT系统的运行效率。

1 混合需求问题的两阶段法

当RFT系统有2个或以上换乘站时，系统将乘客分为2类：①对目标换乘站有特定要求；②目标换乘站为任意换乘站。本研究以第一类情况为例。当RFT系统有多个车场时，其运行模式也可分为2类：①各车场独立运行，各车场仅接或送各自服务范围内的乘客至目标换乘站；②所有车场协同运行，各车场之间协同调度，服务整个RFT系统内的乘客至目标换乘站。本研究以第二类模式为例，基于虚拟车场法[16]，利用虚拟车场串联多条路径成一条路径，对该路径进行协调优化。多换乘站多车场RFT系统的协同运行示意如图1所示。

系统中乘客需求可分为预约需求(车辆发出前乘客发出的乘车申请)和实时需求(车辆发出后乘客对当前班次车辆发出的乘车申请)，本研究采用两阶段法处理混合需求(同时存在预约与实时需求)的问题[17]。两阶段处理流程如图2所示。

从图2中可以看出，第一阶段处理预约需求时，根据预约需求和初始车辆分布，协调优化目标(换乘站、发出车场、发出车型、发车时刻、运行线路和返回车场)。第二阶段处理实时需求时，先建立实时需求的响应规则，再将实时需求分为普通需求和弱势群体的特殊需求。特殊需求应优先响应，若车辆剩余容量不够，则立即发出下一班次车辆进行服务。一般需求需满足车辆容量及最大运行时间约束才响应，否则拒绝响应。根据响应规则对实时需求响应时，先按实时需求的位置与当前车辆的距离从小到大排序。根据判断规则，逐一判断是否响应各个实时申请。根据响应情况，优化当前班次的剩余线路和返回车场、后续班次的运行线路和调度方案，若不能响应则转为预约申请，被下一班次响应。

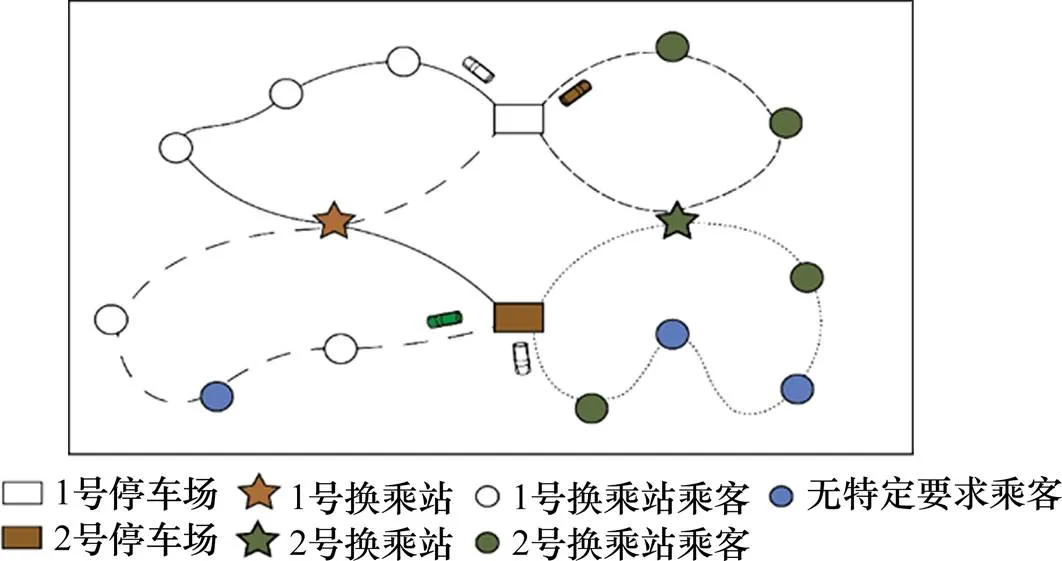
图1 多换乘站多车场响应型接驳公交系统协同运行

图2 两阶段法流程

2 预约需求下多换乘站多车场RFT的协调优化

2.1 基本假设

假设多换乘站多车场RFT系统的服务范围内，乘客需求被系统响应后，不会更改或者取消；车辆以恒定的车速沿各点间固定不变的最短路程行驶，乘客上车后车辆立即启动；乘客在预约的上车时间到达需求点，并只前往预约的目标换乘站；同一需求点乘客的时间窗及目标换乘站相同。

2.2 模型构建

本研究车辆成本包括车辆启动成本、车辆运行成本、车辆早到或晚到产生的成本及其他成本。

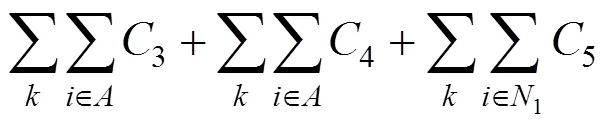
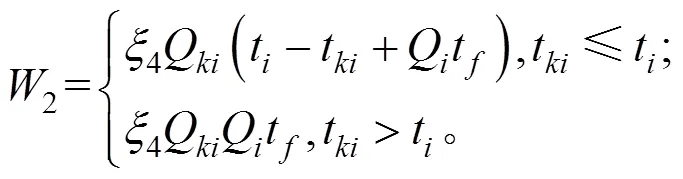
以车辆成本和乘客等待成本组成系统。成本最小为目标，以车辆容量、最大运行时间等为约束构建协调优化模型：

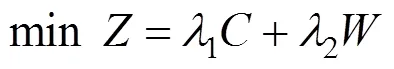
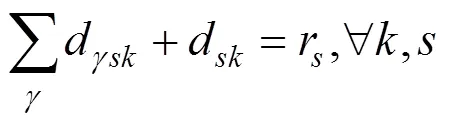
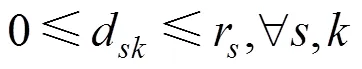
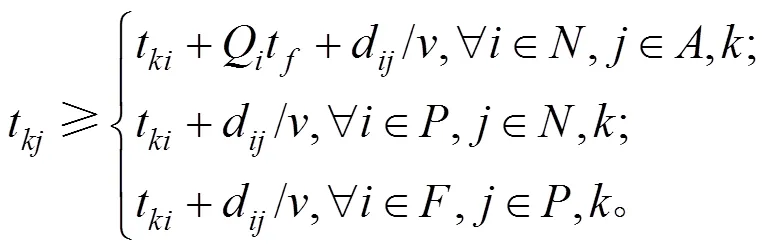
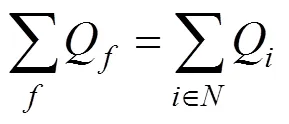
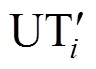
式(2)为车辆早到或晚到成本的计算式。式(3)为乘客等待成本的计算，乘客等待成本包括车辆晚到时的等车成本1、车辆早到时车内乘客等待新乘客的等待成本2与换乘站成本3。式(4)与式(5)分别为2种乘客成本的计算式。式(6)为乘客换乘站成本。式(8)为发车约束，若x=1，即班次发出的车辆经过车场，则说明该车型车辆能从车场发出，那么车场相应车型的车辆保有量大于0；x=0时，该等式恒成立，表明车场相应车型的车辆保有量不小于0。式(9)为车辆数量约束，任意时刻某车型车辆行驶的数量与停放在车场的数量之和为该车型车辆总量。式(10)与式(11)为某车型正在行驶的车辆与停放在停车场的车辆数量不小于0且不大于该车型车辆总量。式(12)确保所有预约的乘客均被车辆送至换乘站。式(13)为车辆的容量约束。式(14)为车辆的单程最大运行时间约束。式(15)为乘客的上车过程，车内人数在车辆到达需求点后增加。式(16)为保障车辆路径的合理性。式(17)表示所有目标换乘站类别的乘客总和为系统收到的乘车申请乘客总量。式(18)表示系统应调度车辆满足乘客的换乘站目标。式(19)表示同一需求点的所有乘客被同一个班次服务。

3 预约需求下协调优化模型的求解

式(1)～(19)的混合整数线性规划为NP-hard问题。为保证计算速度，本研究采用搜索能力较强且收敛速度快的遗传算法[17]。因系统中存在多个换乘站，若采用传统的单链遗传算法，将增大需求点与换乘站之间的不匹配度，会增加非法个体出现的概率。因多染色体遗传算法的个体含有多条染色体，可以较直观地表达多车辆的运行路径，交叉时能避免产生过多的非法解，所以本研究采用多链结构的遗传算法，即多染色体遗传算法。算法流程如图3所示。

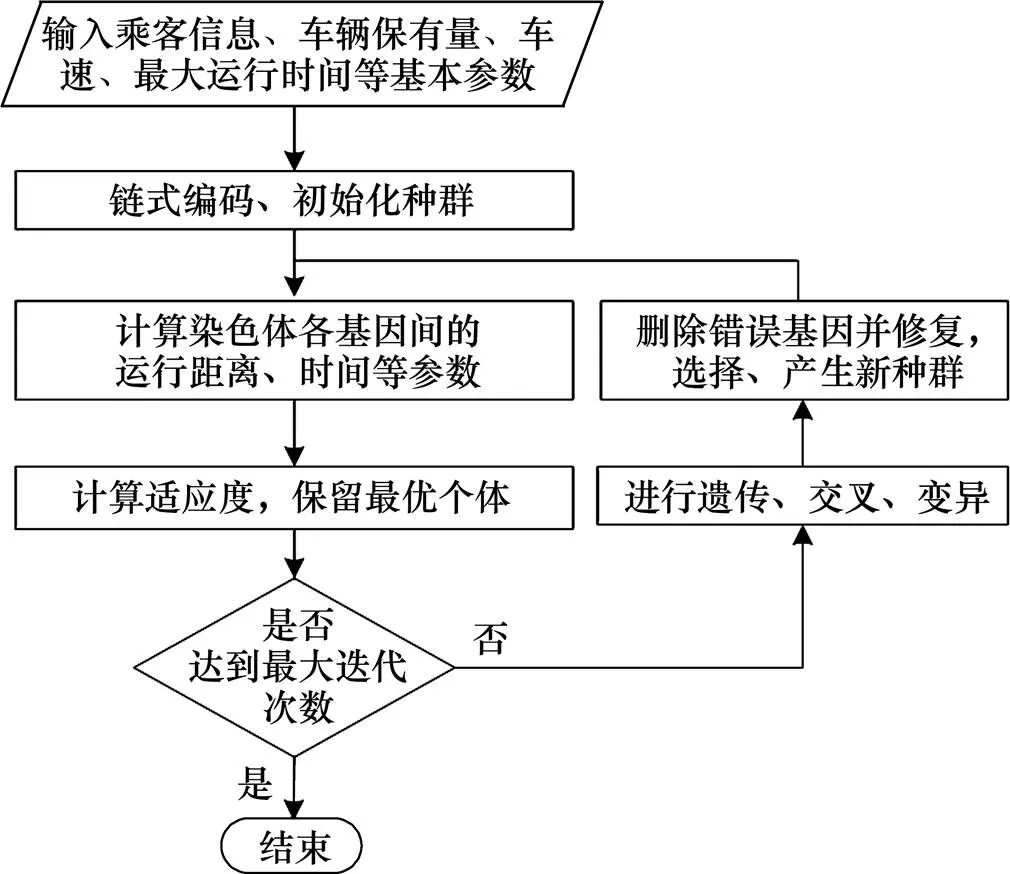
图3 计算流程

图4 编码方式

4 算例分析

4.1 参数说明

设系统中2个换乘站坐标分别为1(1.21, 2.61)、2(3.68, 2.47)；3个停车场的坐标分别为1(1.77, 4.55)、2(2.04, 1.84)、3(4.23, 3.82)；乘客预约需求及实时需求信息见表1、2，乘客目标换乘站信息见表3，其中目标换乘站o是乘客对换乘站没有要求。

为便于计算与对比，根据文献[13]，15分别取值为0.6元/min、0.6元/min、1.2元/min、0.6 元/min和1.2元/min；1和2分别取值为0.4和0.6；车辆最大运行时间max取值30 min，车辆行驶速度取为30 km/h。初始时刻3个车场均拥有1、2、3型号的车辆各2台，其中，1容量为10人，启动成本为5元，单位行驶成本为1元/km；2容量为15人，启动成本为10元，单位行驶成本为1.5元/km；3容量为20人，启动成本为15元，单位行驶成本为2元/km。其他费用在1 h的研究时段内取25元，实时需求被拒绝的单位惩罚费用为5元/人。设种群规模为100，最大迭代次数为100，交叉概率为0.4，变异概率为0.15，锦标赛个体数为5。

表1 预约需求信息

表2 实时需求信息

4.2 运营模式的比较

其他条件不变，按车场协同运营、独立运营分别进行协调优化，优化过程如图5所示，优化结果见表4～6。

表3 乘客目标换乘站信息

图5 收敛过程

由表4～6可知，与独立运营模式相比，协同运营模式的系统总费用减少了14.4%，总运行时间和发车次数分别减少了24.2%和3次，平均满载率增加了13.9%。因此，混合需求下多换乘站系统中，多车场的协同运营模式优于各车场的独立运行。系统协同运行时，因为54号实时需求被班次1拒绝插入，54号需求被当作班次2的预约需求进行重新优化。54号需求点3位乘客加入，班次2发车车型也由小车型1调整为2。多车场独立运行时，分别从车场1、2发出的班次2，乘车人数均为10，但因车场1车型的保有量限制，所以2个班次发出的车型均为2。

表4 多车场协同运营结果

4.3 车型比例对运行线路与调度的影响

其他条件不变时，各车场小车型1数量增加50%，车型3数量减少50%，车辆总数仍为18辆，分析车型比例的变化对多换乘站系统运行结果的影响。车场协同运营、独立运营的优化过程如图6所示，协同运营、独立运营结果见表7～9。

表5 多车场独立运营结果

表6 运营模式的比较

比较表7、8和表4、5可知，初始时刻各车场小型车1增加，有效解决了因1车型的紧缺导致启动成本与车辆行驶成本上升的问题。比较表6、9可知，由于启动成本与行驶成本较低的小型车增加且更合理地利用，独立运营模式与协同运营模式的系统总费用分别下降了7.3%、7.5%，运行时间分别减少了7.1%、2%，协同运营模式的平均满载率基本不变，而独立运营模式的平均满载率上升了6.4%。因此，车型比例的变化对系统产生显著影响。

图6 不同车型比例收敛过程

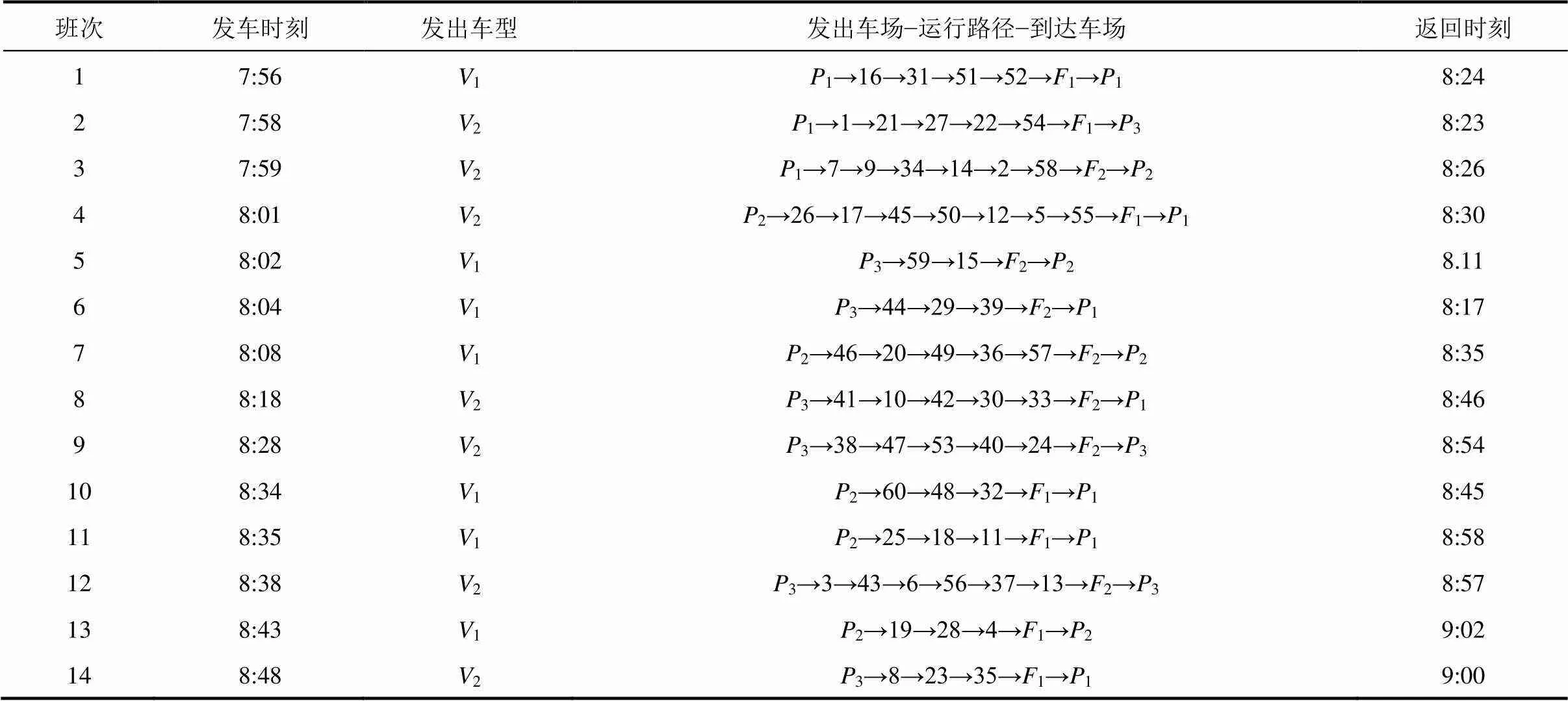
表7 增加车型V1同时减少车型V3后多车场协同运营结果

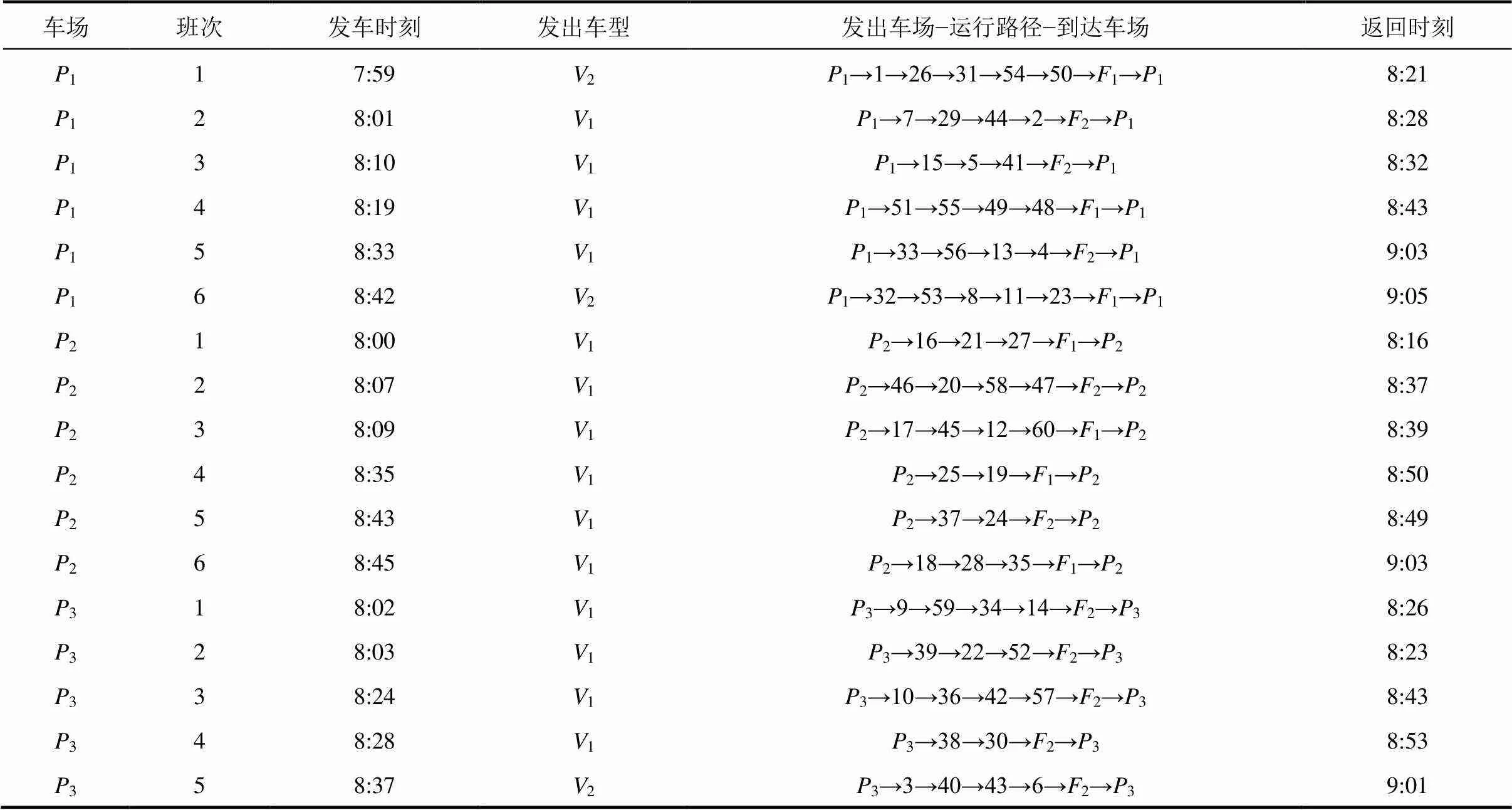
表8 增加车型V1同时减少车型V3后多车场独立运营结果

表9 增加车型V1同时减少车型V3后2种运营方式比较

5 结语

以系统总成本最小为目标，乘客时间窗、车辆容量、最大运行时间等为约束条件，构建了预约需求下多个换乘站、多个车场RFT系统运行路径与调度的协调优化模型，设计了求解算法。考虑了实时需求，构建了混合需求问题的两阶段法。通过算例，得到结论：

1) 利用该方法，能有效获取多换乘站、多车场RFT系统的运行路径和发车时间，验证了本模型的有效性。

2) 车场运营模式和车型比例均是系统运行性能的重要影响因素。

后续研究应考虑动态路网下的协调优化。

[1] Qiu F,Shen J X,Zhang X C,et al.Demi-flexible operating policies to promote the performance of public transit in low-demand areas[J].Transportation Research Part A: Policy and Practice,2015,80:215−230.

[2] Guo Q W,Chow J Y J,Schonfeld P.Stochastic dynamic switching in fixed and flexible transit services as market entry-exit real options[J].Transportation Research Part C: Emerging Technologies, 2018, 94: 288−306.

[3] Edwards D, Watkins K. Comparing fixed-route and demand-responsive feeder transit systems in real-world settings[J]. Transportation Research Record: Journal of the Transportation Research Board, 2013, 2352(1): 128− 135.

[4] Frei C,Hyland M,Mahmassani H S.Flexing service schedules: Assessing the potential for demand-adaptive hybrid transit via a stated preference approach[J]. Transportation Research Part C: Emerging Technologies, 2017, 76: 71−89.

[5] Ghannadpour S F,Noori S,Tavakkoli-Moghaddam R,et al. A multi-objective dynamic vehicle routing problem with fuzzy time windows: Model, solution and application[J]. Applied Soft Computing,2014,14:504−527.

[6] Pan S L,Yu J,Yang X F,et al.Designing a flexible feeder transit system serving irregularly shaped and gated communities: Determining service area and feeder route planning[J]. Journal of Urban Planning and Development, 2015,141(3):04014028.

[7] Lu X L,Yu J,Yang X F,et al.Flexible feeder transit route design to enhance service accessibility in urban area[J]. Journal of Advanced Transportation, 2016, 50(4): 507− 521.

[8] Chen P,Nie Y.Optimal design of demand adaptive paired-line hybrid transit: Case of radial route structure[J]. Transportation Research Part E: Logistics and Transportation Review,2018,110:71−89.

[9] Rahimi M,Amirgholy M,Gonzales E J.System modeling of demand responsive transportation services: Evaluating cost efficiency of service and coordinated taxi usage[J]. Transportation Research Part E:Logistics and Transportation Review,2018,112:66−83.

[10] Shen Y D,Wang S Q.Maximal synchronization of feeder buses to metro using particle swarm optimization[C]// Bio-Inspired Computing--Theories and Applications, 2015: 350−361.DOI:10.1007/978-3-662-49014-3_32.

[11] Engelen V,Matti,Cats O,et al.Enhancing flexible transport services with demand-anticipatory insertion heuristics[J]. Transportation Research Part E: Logistics and Transportation Review,2018,110:110−121.

[12] 邱丰,李文权,沈金星.可变线路式公交的两阶段车辆调度模型[J].东南大学学报(自然科学版),2014,44(5): 1078−1084. (QIU Feng, LI Wen-quan, SHEN Jin-xing. Two-stage model for flex-route transit scheduling[J]. Journal of Southeast University (Natural Science Edition), 2014,44(5):1078−1084.(in Chinese))

[13] 王正武,袁媛,高志波.高自由度响应公交分区路径与调度的协调优化[J].长沙理工大学学报(自然科学版),2018, 15(1):41−48.(WANG Zheng-wu, YUAN Yuan, GAO Zhi-bo.Coordination optimization for partition path and scheduling with high degree of freedom demand response transit[J].Journal of Changsha University of Science & Technology (Natural Science), 2018, 15(1): 41−48. (in Chinese))

[14] 王正武,陈涛,宋名群.同时接送模式下响应型接驳公交运行路径与调度的协调优化[J].交通运输工程学报, 2019, 19(5): 139−149. (WANG Zheng-wu, CHEN Tao, SONG Ming-qun. Coordinated optimization of operation routes and schedules for responsive feeder transit under simultaneous pick-up and delivery mode[J]. Journal of Traffic and Transportation Engineering, 2019, 19(5): 139−149.(in Chinese))

[15] 宋名群.混合需求下多换乘点响应接驳型公交运行线路的协调优化[D].长沙:长沙理工大学,2019.(SONG Ming-qun. Coordinated optimization of multiple transfer points responsive feeder transit operation route under mixed demand[D]. Changsha: Changsha University of Science & Technology,2019.(in Chinese))

[16] 葛显龙,王旭,邓蕾.基于联合配送的开放式动态车辆路径问题及算法研究[J].管理工程学报,2013,27(3):60−68. (GE Xian-long, WANG Xu, DENG Lei. Research on open and dynamic vehicle routing problems based on joint distribution[J]. Journal of Industrial Engineering and Engineering Management, 2013, 27(3): 60−68. (in Chinese))

[17] 王正武,易童翔,高志波.响应型接驳公交运行路径与车辆调度的协调优化[J].交通科学与工程,2018,34(1): 68−73.(WANG Zheng-wu, YI Tong-xiang, GAO Zhi-bo. Coordinated optimization of running route and vehicle scheduling for responsive feeder transit[J]. Journal of Transport Science and Engineering, 2018, 34(1): 68−73. (in Chinese))

Coordinated optimization of responsive feeder transit with multiple depot and transfer station

WANG Shun1, LIU Jie2, JIANG Ning-yu2, WANG Zheng-wu2

(1. Changsha Construction Project Quality and Safety Supervision Station, Changsha 410016, China;2. Hunan Key Laboratory of Smart Roadway and Cooperative Vehicle-Infrastructure Systems, Changsha University of Science & Technology, Changsha 410114, China)

In order to improve the operational efficiency of responsive feeder transit, an idea of method for responsive feeder transit system was proposed. Which consists of the coordinated operation of multiple depots and transfer stations, the coordinated design of running routes, and the vehicle scheduling. Considering the mixed demand of reservation and real-time, the two-stage model of responsive feeder transit system was built to coordinate the running routes and vehicle scheduling. The multi- chromosomes genetic algorithm was then designed. The results show that, under the same conditions of mixed demand, the total cost, the running time and the number of departures of the collaborative operation mode is reduced by 14.4%, 24.2%, and 3 times respectively, compared with the independent operation. By increasing the proportion of small vehicle to 50%, the total system cost of the independent operation and the collaborative operation is reduced by 7.3% and 7.5% respectively.

two-stage method; multi-depot; multiple transfer station; responsive feeder transit

U491.1

A

1674 − 599X(2021)02 − 0076 − 09

2020−07−23

国家自然科学基金(51678075)；湖南省重点领域研发计划项目(2019SK2171)

王顺(1972−)，男，长沙市建设工程质量安全监督站高级工程师。