可变勾股模糊VIKOR水资源系统韧性评价调控模型及应用

杨亚锋，王红瑞，巩书鑫，邓彩云

（1.北京师范大学 水科学研究院 城市水循环与海绵城市技术北京市重点实验室，北京 100875；2.华北理工大学 理学院，河北 唐山 063000）

1 研究背景

水资源是人类赖以生存和发展的基础，各种水问题频发促使人类思考更合理的水资源可持续利用策略［1-4］。作为研究热点之一，安全评价与风险管理是实现水资源系统可持续发展的重要途径［5-6］。近年来，韧性理念逐渐在城市水资源系统的研究中受到关注［7-9］。

韧性（Resilience）一词源自拉丁语中的“Resilio”，是“复位到原始状态”的意思。与风险分析相比，韧性研究更强调系统本体具备的应对外来冲击的能力。不同学者对水资源系统韧性有着不同理解：我国学者俞孔坚等［10］提出了水系统韧性的概念，认为水系统具备韧性的特征。Alessa 等［11］在已有水资源评价指数的基础上建立了水资源脆弱性指数，用以表达水资源系统韧性。Sandoval-Solis 等［12］以“赤字”为衡量值，从可靠性、恢复性和脆弱性三个方面建立了水资源可持续性指标。Yang 等［13］以尼泊尔河流域为研究对象，结合Sandoval-Solis 等的“赤字”概念，从稳定性、恢复性和脆弱性三个方面衡量水资源的可持续性。Huang 等［14］利用GIS 和ABM 模型对城市水系统韧性开展研究。在以上研究的基础上，作者认为水资源系统韧性指水资源系统及其基本功能在受到自然或人类活动干扰时，具备恢复原有水资源系统功能，并达到新的适应平衡的特性，这个恢复包含了自然和人工的调控作用。

水资源系统是一个复杂多因素系统，与经济、社会和生态环境等多个系统之间存在密切的耦合关系，其韧性评价必然面临多准则决策（Multiple-Criteria Decision Making，MCDM）问题［15］。多准则决策是指在具有相互冲突、不可公度性（Non-commensurable）的方案集中进行选择的决策，其主要目标是在考虑多个属性的情况下，选择最优方案或进行方案排序。综合考虑水资源系统的影响因素，对其韧性水平进行时空排序，进而分析其演化规律，开展水资源系统韧性的评价与调控，对于水资源系统的安全维护和可持续发展策略的制定具有重要的指导意义。

勾股模糊集方法是多准则决策过程中决策矩阵的重要获取途径之一。Yager等［16-17］研究了勾股模糊数（Pythagorean Fuzzy Numbers，PFNs）和复数之间的联系，讨论了一种决策方法，随后定义勾股聚类算子，并应用于新的MCDM 问题处理技术之中［18］。Zhang 等［19-20］提出了基于备择方案与理想解的相似性度量的PF（Pythagorean Fuzzy，PF）-MCDM 决策方法。Ma 等［21］构建了对称勾股模糊算子并应用于MCDM 问题中。Ren 等［22］开发了勾股模糊集用于交互式多准则决策的方法；李德清等［23］基于距离测度，结合排序函数构建了一种勾股模糊集多属性决策模型。

近年来，将勾股模糊集与VIKOR（Vlsekriterijumska Optimizacija I KOmpromisno Resenje，VIKOR）方法融合，结合正负理想点和距离测度进行排序与决策是一个前沿的研究方向。如：Muhammet Gul等［24］以矿山安全风险评价为例，将勾股模糊VIKOR 方法应用于职业风险评价，融合考虑职业健康安全专家在主观判断过程中感知的不确定性和模糊性，提出一种新的职业健康安全风险评估方法来确定风险等级；Liang 等［25］在传统VIKOR 方法的基础上，通过引入TODIM（an acronym in Portuguese for Interactive Multi-criteria Decision Making，TODIM）处理决策者的心理行为，定义勾股模糊熵和交叉熵测度，提出了一种折衷解决方案的新视角，并应用于加纳银行业网上银行网站质量的评价；Pratibha R 等［26］基于勾股模糊熵和散度将勾股模糊集VIKOR 方法应用于印度可再生能源技术的评价之中，等等。可见，勾股模糊集与VIKOR 方法的融合，已经在诸多领域取得了成功应用，但在以往研究中，勾股模糊决策数往往依据专家经验进而通过语言量表对应获得，相邻等级之间具有绝对分明的边界。而事实上，特定指标下某一待评对象的状态，往往在两个相邻等级之间模糊存在；若绝对地将其归为某一等级，则均会损失一定的客观性。以水资源系统韧性为例，若某一指标的值处在［20，30］为一级，对应勾股模糊数为［0.85，0.15］；处在［30，40］为二级，对应勾股模糊数为［0.75，0.25］，那么如果某一待评对象的该指标值为30，则需考虑如何确定其勾股模糊数。根据可变集相对隶属度的方法，该待评对象对于该指标应该在一级和二级之间对立统一，这符合人们的思维认知。

基于此，首先采用可变集相对隶属度的方法获取勾股模糊决策矩阵，构建一种可变勾股模糊VIKOR 多准则评价模型；其次从韧性视角出发，构建指标体系与等级标准，进一步将模型应用于长江经济带的水资源系统韧性评价，给出调控策略，为该区域的水资源安全和可持续发展提供支持。

2 主要方法

水资源系统是一个复杂系统，其韧性水平及影响因子往往具有模糊不确定性。模糊隶属函数是解决该类问题的有效手段之一。然而，由于水资源系统和人类思维的复杂性，传统的隶属度已不能满足实际决策需求。勾股模糊集、可变模糊集等几种新的工具应运而生。本文主要利用可变集中相对隶属度方法对勾股模糊集进行改进，进而与VIKOR多目标决策方法进行融合拓展研究。

2.1 勾股模糊集勾股模糊集（Pythagorean Fuzzy Sets，PFSs）放宽了直觉模糊集理论中隶属度与非隶属度之和小于等于1 这一条件，约定隶属度与非隶属度之和可以超过1，但其平方和不超过1。勾股模糊集中的隶属度和非隶属度对应勾股定理中的两个勾股数，故Yager 形象地称其为勾股模糊集［16］。对于水资源系统的抵抗性、恢复性和适应性水平，从隶属度和非隶属度两方面综合表达更符合人们的思维认知。

设论域X上的一个勾股模糊集PFSs指的是如下形式的一个集合：

其中uP:X→[0,1]，vP:X→[0,1]。若满足对于任意xi∈X，(uP(xi))2+(vP(xi))2≤1，则分别称uP和vP为xi对P的隶属度和非隶属度，称为xi对P的犹豫度或不确定度。

若将隶属度uP（xi）和非隶属度vP（xi）看作二维直角坐标系中横坐标轴和纵坐标轴上的向量，则视为隶属度与非隶属度向量的模，称为勾股模糊集P的自信度；自信度的作用效果与rP(xi)和uP(xi)所在方向的夹角有关。

设rP(xi)和uP(xi)所在方向的夹角为θP(xi)，Yager 定义了一个刻画自信度rP(xi)方向的量dP(xi)，称为自信度的方向［16］。 其中，dP(xi)∈[0,1]， 且vP(xi)=rP(xi)sin(θP(xi))。

Zhang 等［19］记p=（up，vp），称其为勾股模糊数（PFNs）。相应地称为p的自信度；为p的犹豫度。

2.2 勾股模糊熵与散度水资源系统是一个多因子耦合系统。确定各因子的权重，对于评价与调控至关重要。熵和散度是勾股模糊集理论中的重要概念，也是权重确定的主要工具。Pratibha-Rani等［26］在直觉模糊熵的基础上定义了勾股模糊集的PF 熵和PF 散度。在PF 熵和PF 散度的基础上给出勾股模糊数（PFNs）的熵和散度。

设勾股模糊数p=（up，vp），则其PF-熵为

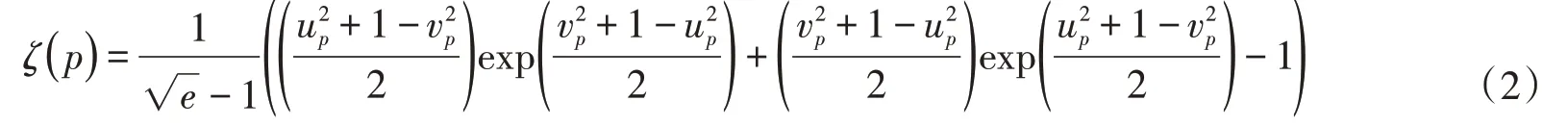
当up+vp=1时，上式可简化为

设有勾股模糊数p=（up，vp），t=（ut，vt），其散度可表示为

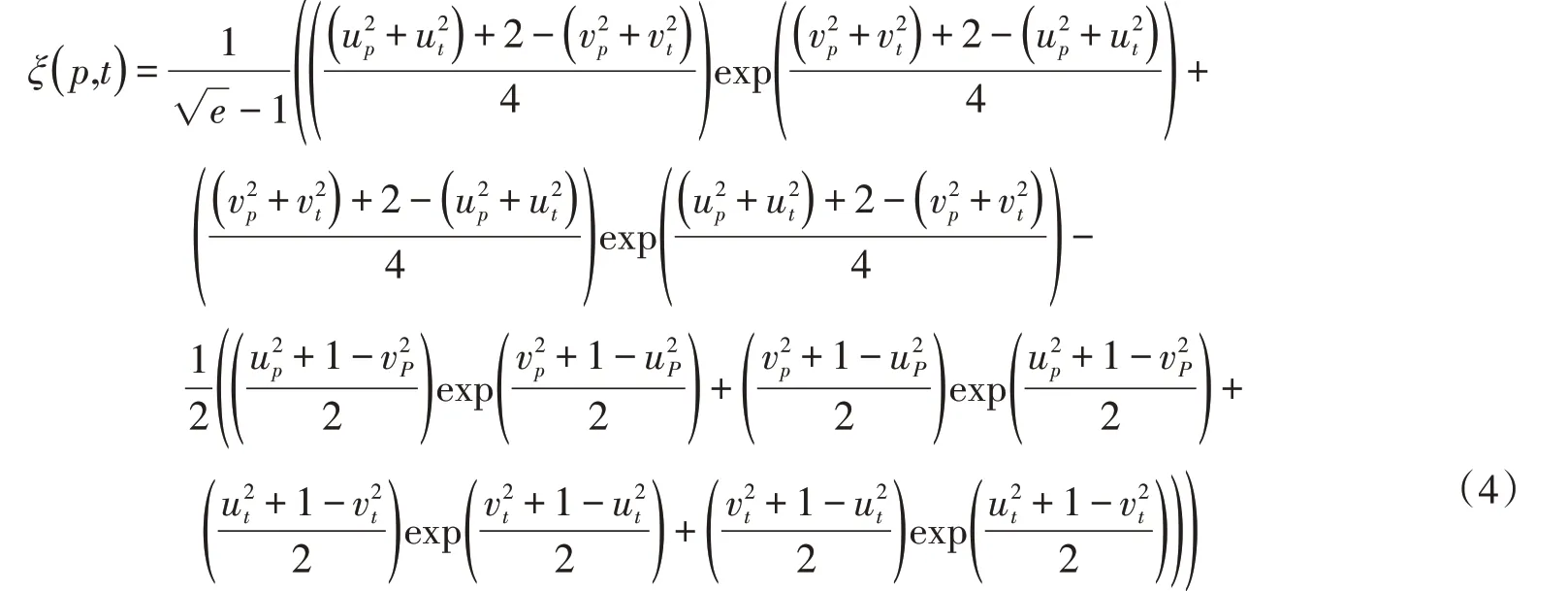
当uP+vP=1时，上式可简化为

2.3 可变集与相对隶属函数由于水资源系统韧性相邻等级之间没有明确的边界，评价对象关于某个指标的等级也具有模糊性，应该介于两个相邻等级之间，且满足对立统一性。陈守煜先生［27］于2005年提出的可变集方法是解决此类问题的有效手段。

可变集方法针对经典集合和模糊集合只研究静态事物、现象与概念的问题，考虑事物变化过程中呈现出“非此即彼”的清晰性与“亦此亦彼”的模糊性两者辩证对立统一的特性，提出了动态相对隶属度概念，是对模糊隶属度的一种拓展研究，已在水资源系统分析研究中得到了成功应用［27-29］。

可变集针对研究对象的对立清晰属性进行研究，在向对立面转化过程中，其隶属程度可用对立测度值来衡量，它们随时空条件的变化而变化，但其对立测度值之和恒为1。

设O为评价对象集合，o∈O，o的对立清晰属性记以A与Ac。映射

称为o对A与Ac的动态对立相对隶属函数。

设评价对象集为O={oi} (i=1,2,…,m)，Xij=(xij)为对象oi的各指标cj(j=1,2,…,n)的值。指标cj分为s个等级，s个等级的指标值区间矩阵为：

其中ajh、bjh为指标cj在h级别标准值区间的上下限。

根据可变集对立统一定理，在级别h值区间中必定存在指标cj的级别h与级别h+1 的渐变式质变点kjh，质变点两侧对应两级别相互对立。

由式（8）与矩阵I得矩阵K，K=[kjh，bjh]，若指标值xij在矩阵K相邻两级h与h+1区间，则xij对h级的相对隶属度计算方法如下：

对于小于h级，大于h+1级的指标cj的相对隶属度均为0，即：μj(h+1)(oi)=0。

2.4 VIKOR方法水资源系统韧性评价是一个多准则多目标的复杂决策问题。在获取各研究对象关于各指标的勾股模糊隶属度之后，需要综合考虑各指标之间的序关系及相互作用。作为多准则决策MCDM 的重要方法之一，VIKOR 方法于1998年由Opricovic 首次提出，其主要目的是根据Lq-度量挖掘出一个折衷解决方案，使其在排序过程中更加接近理想解［30-31］。根据散度的定义，评价对象oi(i=1,2,…,m)的Lq-度量公式为

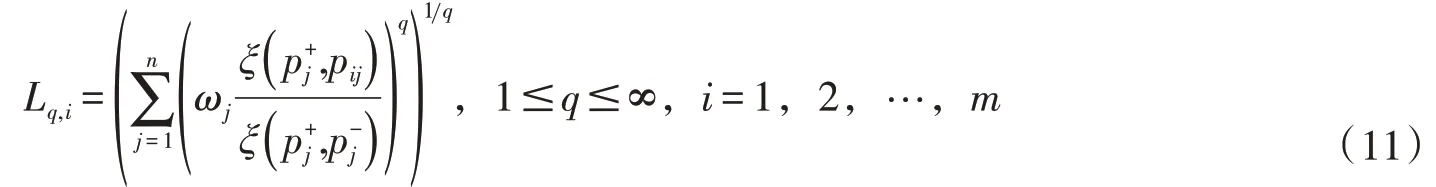
其中，ωj(j=1,2,…,n)是各指标对应的权重。和是第j个指标的正理想解和负理想解。Lq，i代表评价对象oi和理想解之间的距离。这种方法提供的折衷解决方案，满足最大群体效益和最小个体遗憾，其度量分别为L1，i和L∞，i。

3 可变勾股模糊VIKOR水资源系统韧性评价调控模型设计

水资源系统韧性评价是个多指标决策过程，实施态势评价与演化分析是韧性调控的前提。本文构建的模型算法设计如下：设有m个研究对象，记作o1，o2，…，om。评价与调控指标体系包含n个指标c1，c2，…，cn。对每个研究对象进行评判，进而所有对象进行优选排序；在评价排序的基础上，结合实际情况提出调控策略。下面给出基于可变勾股模糊VIKOR多指标评价的具体步骤。

步骤1。勾股模糊决策矩阵。在实际应用中，一个关键的问题是合理估计PF 集的隶属函数。目前，通过语言评分系统构建PF 数据的是普遍采用的一种勾股模糊的获取方法。结合对水资源系统韧性评价调控认知，这里采用五点语言评价量表及其对应的PF值［32］。见表1。

表1 勾股模糊语言变量与勾股模糊数、韧性等级的对应关系

根据研究对象的实际指标值，利用可变集方法计算关于5个等级的相对隶属度；若研究对象oi关于各个指标cj的相对隶属度为μjh(oi)和μjh+1(oi)，则其oi关于指标cj的勾股模糊隶属度期望值为pij=μjh(oi)ph+μjh+1(oi)ph+1，记作pij=。

步骤2。基于PF 熵和散度确定权重。设各指标的权重为ω1，ω1，…，ωn，且满足条件0≤ωj≤1，且基于PF熵式（3）和PF散度式（5）的指标权重计算公式［26］如下：

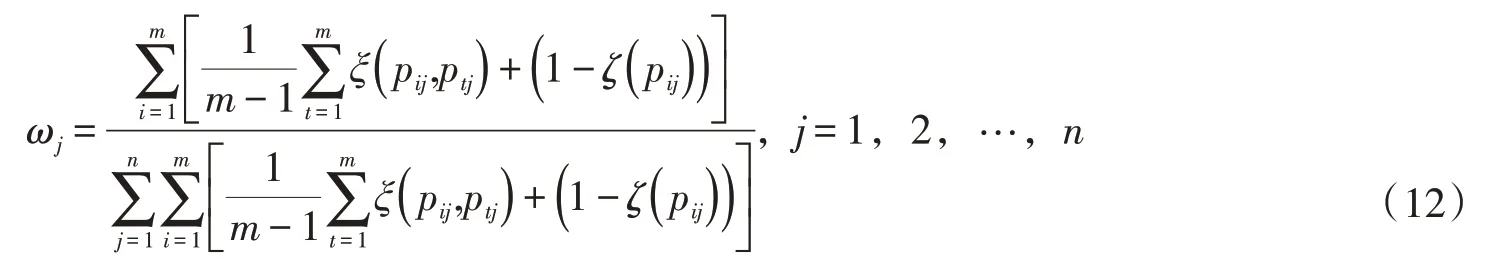
步骤3。确定正负理想点。比较所有研究对象o1，o2，…，om关于同一指标cj()j=1，2，…，n的勾股模糊数值pij=(i=1,2,…，m)，确定指标cj下的最优值和最劣值进而得到正理想指标值向量p+={p+1,p+2,…，p+n} 和负理想指标值向量

步骤4。计算利益比率。计算每个评价对象oi（i=1，2，…，m）的最大群体效益值Si、最小个体遗憾值Ii和利益比率值Qi，如下：

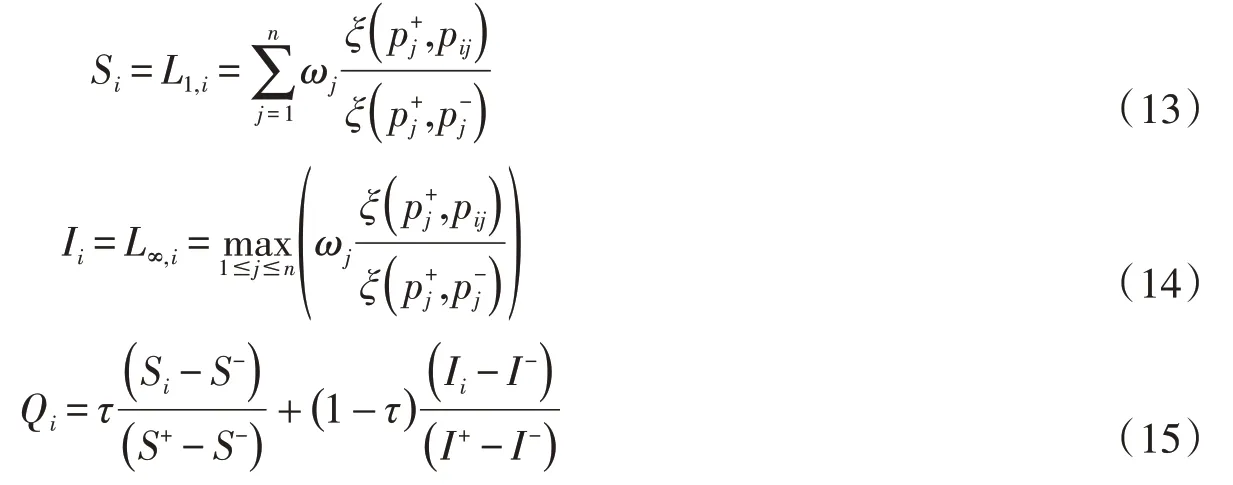
其中，S+=maxSi，S-=minSi，I+=maxIi，I-=minIi，τ∈[0,1]为决策系数。

步骤5。韧性水平排序。令Ri=1-Qi，称为韧性排序值，则有：Ri越大，韧性水平越高。

步骤6。调控指标挖掘。针对指标cj(j=1，2，…，n)分别重复步骤4—5。对象oi()i=1,2,…,m的排序值记为Rij。设定阈值θ，进行异常检测。若Rij<θ，则oi在cj下被判定为“劣”，否则为“优”。在指标cj下，若研究对象被判定为“劣”的个数则cj异常，为重点调控指标。

本文构建的水资源系统韧性评价模型流程图，见图1。

图1 算法流程图

4 实例分析

4.1 研究区选择及数据来源长江经济带是指沿长江附近的经济圈，东起上海，西到云南，幅员辽阔，覆盖上海、江苏、浙江、安徽、江西、湖北、湖南、重庆、贵州、四川、云南等11 个省市，面积约205.23 万km2，占全国的21.4%，人口和生产总值均超过全国的40%。近年来受人类活动和气候变化等影响，长江水环境恶化、水生态脆弱、水资源短缺与水旱灾害等问题日趋严重。因此，开展该区域水资源系统的韧性研究，制定相应的调控策略对长江经济带水资源可持续利用、生态优先与绿色发展可持续战略的实施有重要的意义。

本文所有数据均来源于上海等11 个省级行政区的地方统计年鉴（2009—2018年）、地方水资源公报（2009—2018年）以及中国统计年鉴（2009—2018年）。

4.2 指标体系构建韧性可以看作系统提升适应性并不断适应风险与扰动的这一循环过程。在这一过程中，系统经历了从风险冲击到冲击后维持自身稳定再到迅速恢复，甚至将危机转变为机遇，实现创新发展等的不同阶段。基于该理念，本研究结合以往水资源或水系统韧性研究［10］，将水资源韧性分为扰动前、扰动中和扰动后三个子过程，分别对应抵抗性、恢复性和适应性三个目标。水资源系统的韧性过程就可分解为：（1）受到干扰前，水资源系统能够抵御干扰的能力；（2）受到干扰时，水资源系统恢复快慢的反应能力；（3）受到干扰后，系统能够在此次干扰中习得的适应能力。

考虑水资源系统面临压力的多元性、复合性与吸收扰动的能力。水资源系统韧性取决于生态环境、地区空间结构、经济社会、人口以及管理制度等各子系统间的相互作用，从抵抗性、恢复性和适应性三个方面，结合科学性、合理性以及可获取性的原则来确定相应指标。

（1）抵抗性指标。抵抗性指标是指水资源系统在受到冲击时，能够抵御冲击的能力。在水资源系统中，其面临的潜在风险越大，受到的干扰就会越多，其抵抗性也就会相应越弱。当区域内洪涝、干旱等外生性因素越多，水资源系统遭受的冲击就会越大，系统抵抗风险的能力越弱，韧性在抵抗性过程中的表现就会越差。相应地，当区域内水资源压力、人口压力等内生性因素同样会导致水资源系统遭受巨大冲击，导致抵抗风险能力变弱。

（2）恢复性指标。恢复性指标是指水资源系统受到冲击后，恢复至受冲击前状态的能力。在水资源系统中，恢复的过程受到水环境、经济以及用水结构等内部因素影响，区域内部因素决定了系统恢复过程的快慢。从影响恢复性的主体看，可以分为环境、生态、经济、社会等几个方面：例如，污水的处理决定了水环境的承载能力；经济结构影响用水结构，经济发展水平影响用水效率，而农业、工业用水则远大于第三产业用水；不同的用水效率、能耗效率也会影响水资源的韧性水平等。

（3）适应性指标。适应性指标是指在水资源系统在受到冲击并恢复后，能够在其中学习到的适应能力。水资源系统的适应过程，主要受到区域内的创新因素、保障因素等影响。不同的适应水平决定了系统在下一次受冲击时，能够迁移到的新的初始状态水平。在水资源系统中，对适应性的影响主要集中在区域可持续发展以及水资源可持续利用等方面。

根据以上指标体系构建原则及范围，构建水资源系统韧性评价指标体系。参考相关文献及行业标准［33-36］，结合长江经济带实际情况，制定等级标准。具体见表2。

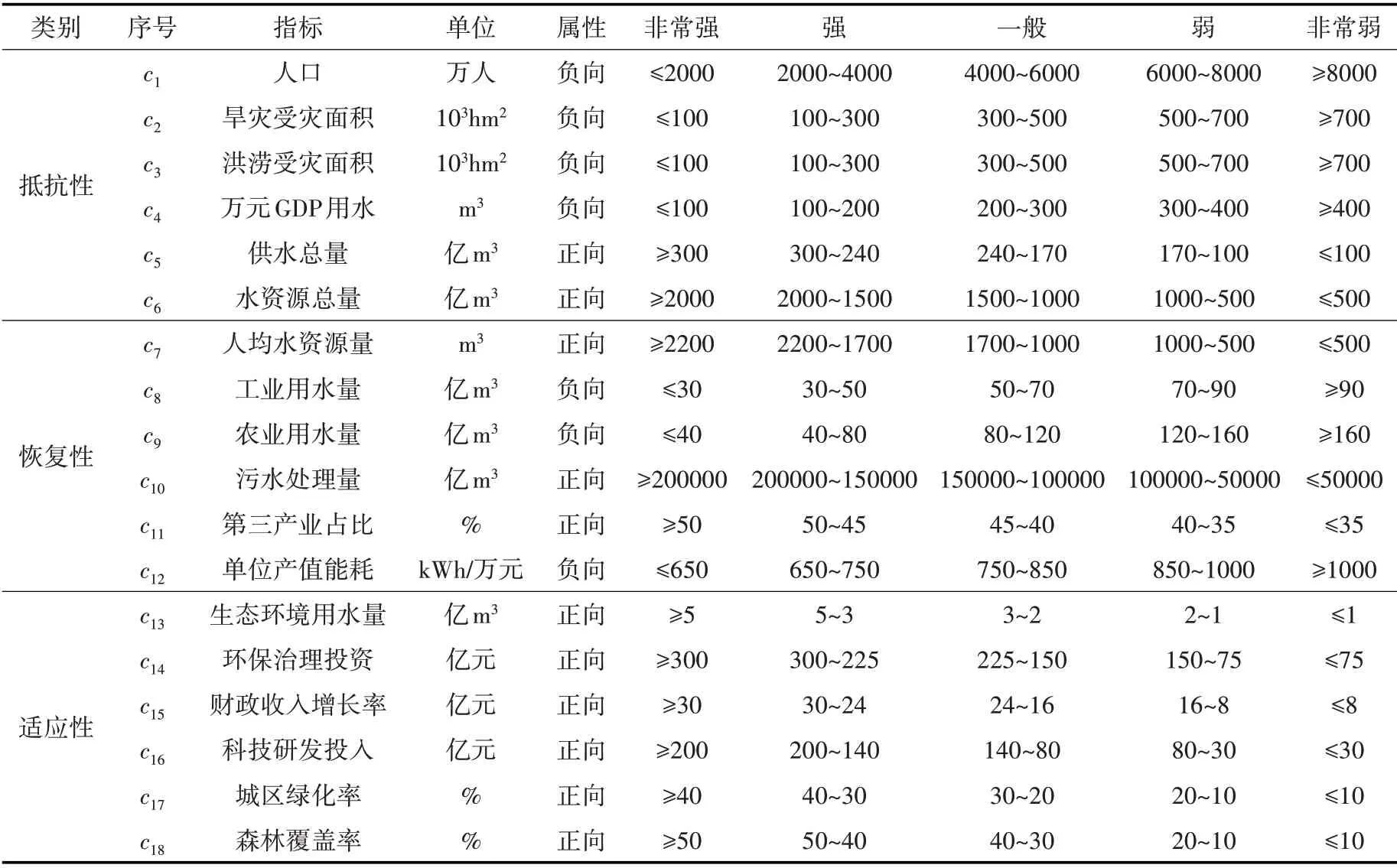
表2 长江经济带水资源系统韧性评价指标体系及等级标准

4.3 模型实施基于以上数据和标准，利用构建的韧性评价模型对长江经济带2008—2017年水资源系统韧性的时空演化过程与调控策略展开研究，具体步骤如下：

步骤1，根据11 个省级行政区各指标数据的平均值，利用可变集相对隶属度方法，结合PF 五级评分表，计算勾股模糊决策矩阵，见表3。

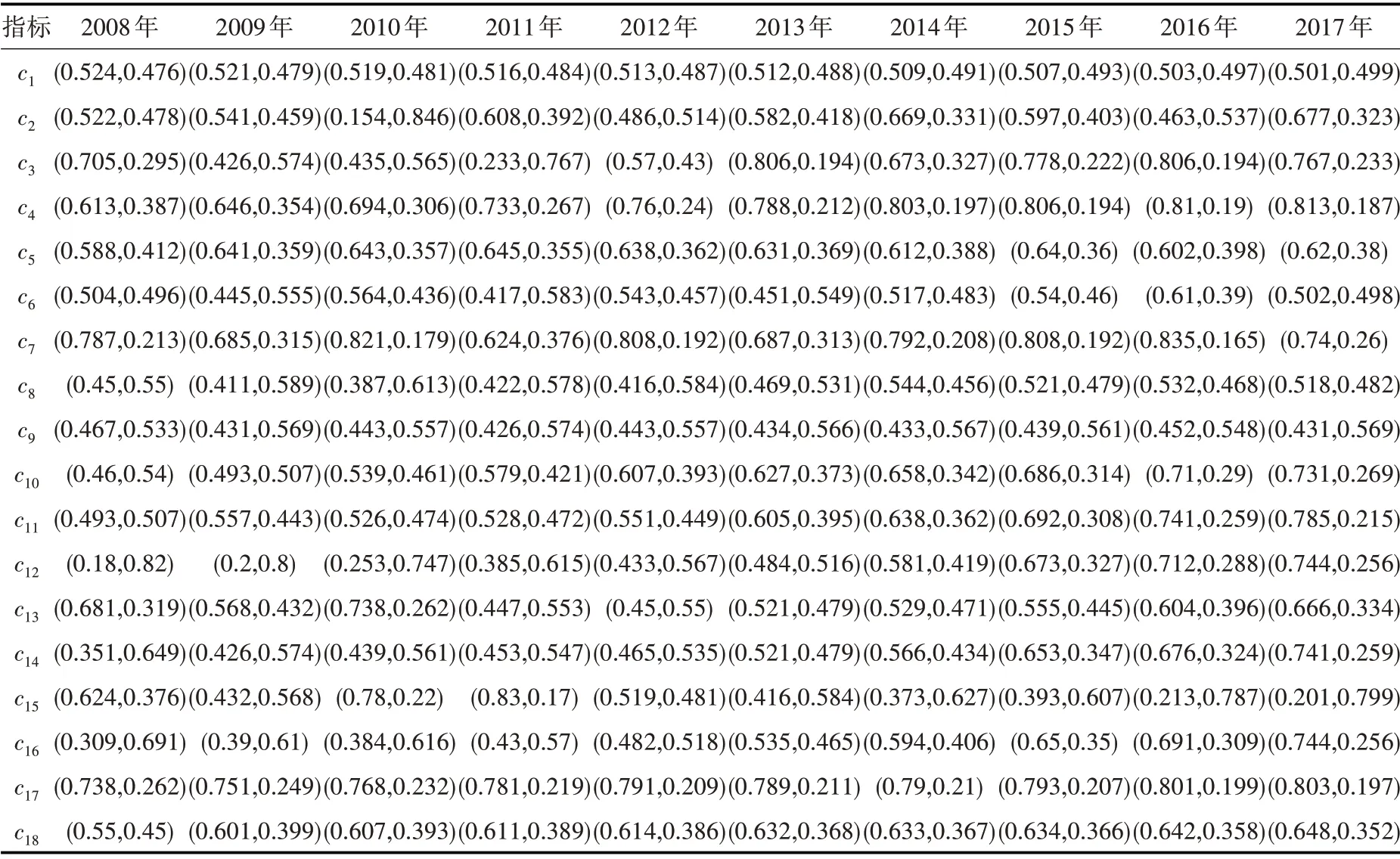
表3 长江经济带2008—2017年水资源韧性勾股模糊数

步骤2，基于11个省级行政区10年的总数据，利用式（12）计算各指标的权重，见表4。

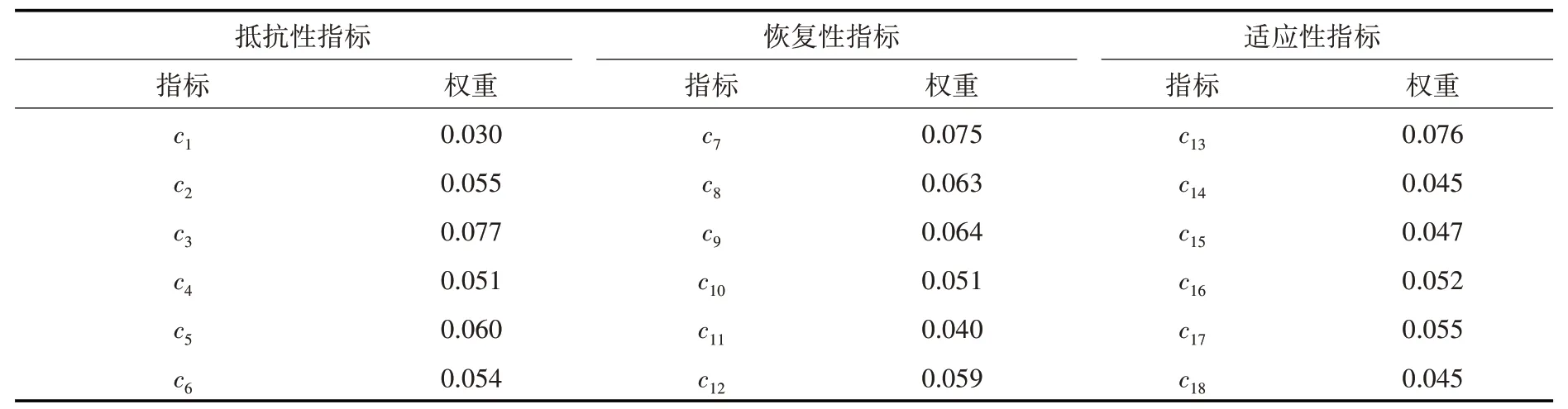
表4 长江经济带2008—2017水资源韧性指标权重

步骤3，计算各指标的正理想点和负理想点，见表5。

表5 长江经济带水资源韧性-各指标的正理想点和负理想点

步骤4，利用式（13）—（15）计算各年度的群体效益S、个体遗憾I和韧性排序值R。具体见表6。

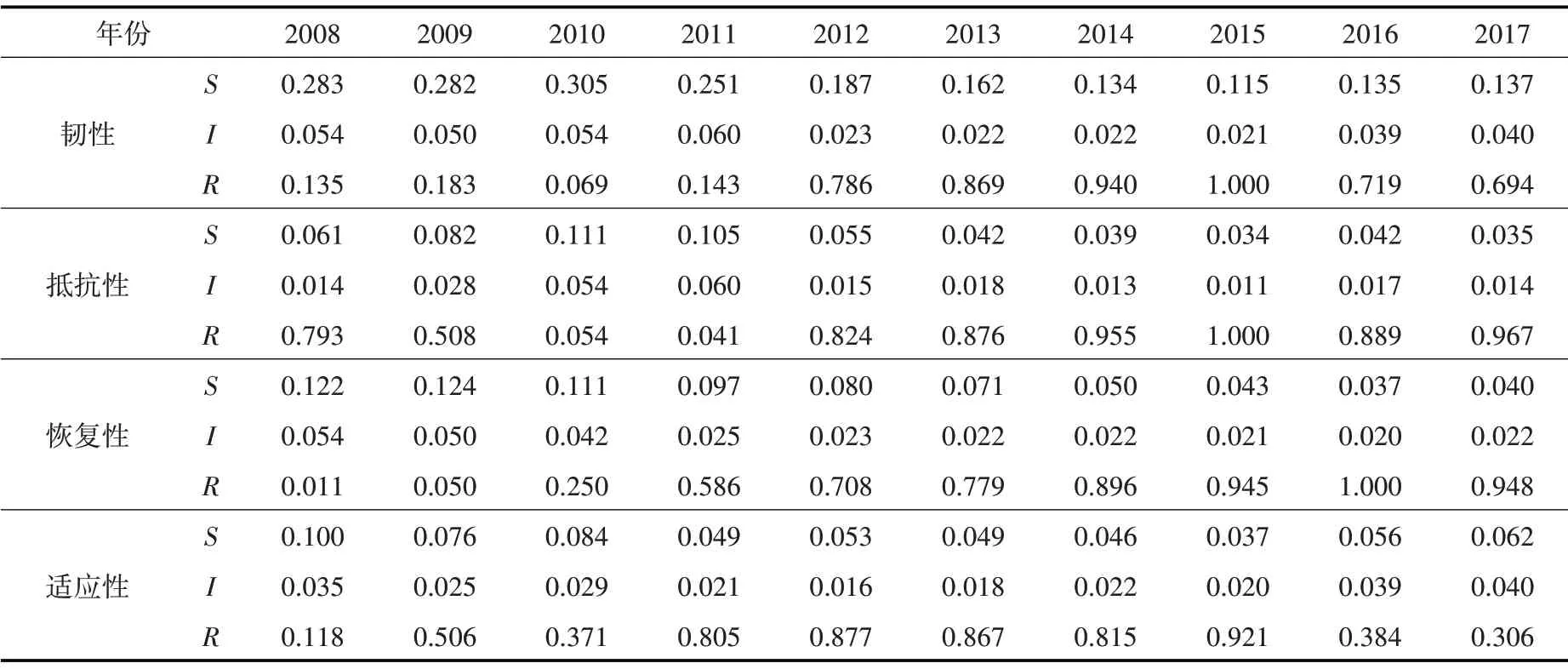
表6 长江经济带2008—2017年水资源韧性结果

步骤5，长江经济带各年度的韧性排序结果见图2。各省区韧性及各方向的时空演化见图3。

4.4 分析与讨论由图2可知：长江经济带2008—2017年水资源系统韧性总体上呈现逐年提升的态势。2008—2011年，韧性值稳定于较低水平，2010年出现最低值；2011年之后，长江经济带水资源系统韧性得到了明显的提升，在2015年出现峰值。随后适应性水平的大幅下滑，韧性开始出现了一定程度的降低，其主要原因是财政收入增长率放缓，由2015年的12.56%下降至2016年的5.04%，同比下降60%；该指标水平大幅降低，其他的适应性指标水平仍呈现缓慢上升。因此，总体来看，适应性子系统的韧性排序值从0.921骤降至0.384，形势严峻，是目前韧性的重点调控方向。

图2 长江经济带2008—2017年水资源系统韧性趋势

由图3（a）可知，长江经济带11 省的水资源系统韧性均处于逐年上升的态势，江苏等部分省份在从2015年开始出现不同程度的下降；根据图3（b），近年来，长江经济带水资源系统的抵抗性同样呈现逐年提升的趋势，但是上海、浙江和湖南等省区的抵抗性出现了严重的下降。其中上海市下滑最为严重，由于水资源禀赋较差，且人口密度持续增加，水资源系统抵抗性逐年下降。上海市人口的持续增长和工业化水平的日益提高，给水资源供需关系和水资源可持续利用等带来了冲击。图3（c）展示了恢复性的稳定增长态势，但江西等省区在2016—2017年出现了急剧下降，其中2017年人均水资源量同比下降了26%，但工业用水量却增加了52%；根据图3（d）可知，云南、贵州、安徽和湖南等省区的适应性水平得到了明显的提升，而江苏、上海和浙江等省区则处于较低水平。各省可根据自身实际情况，因地制宜，精准施策，制定相应的水资源系统韧性调控策略。

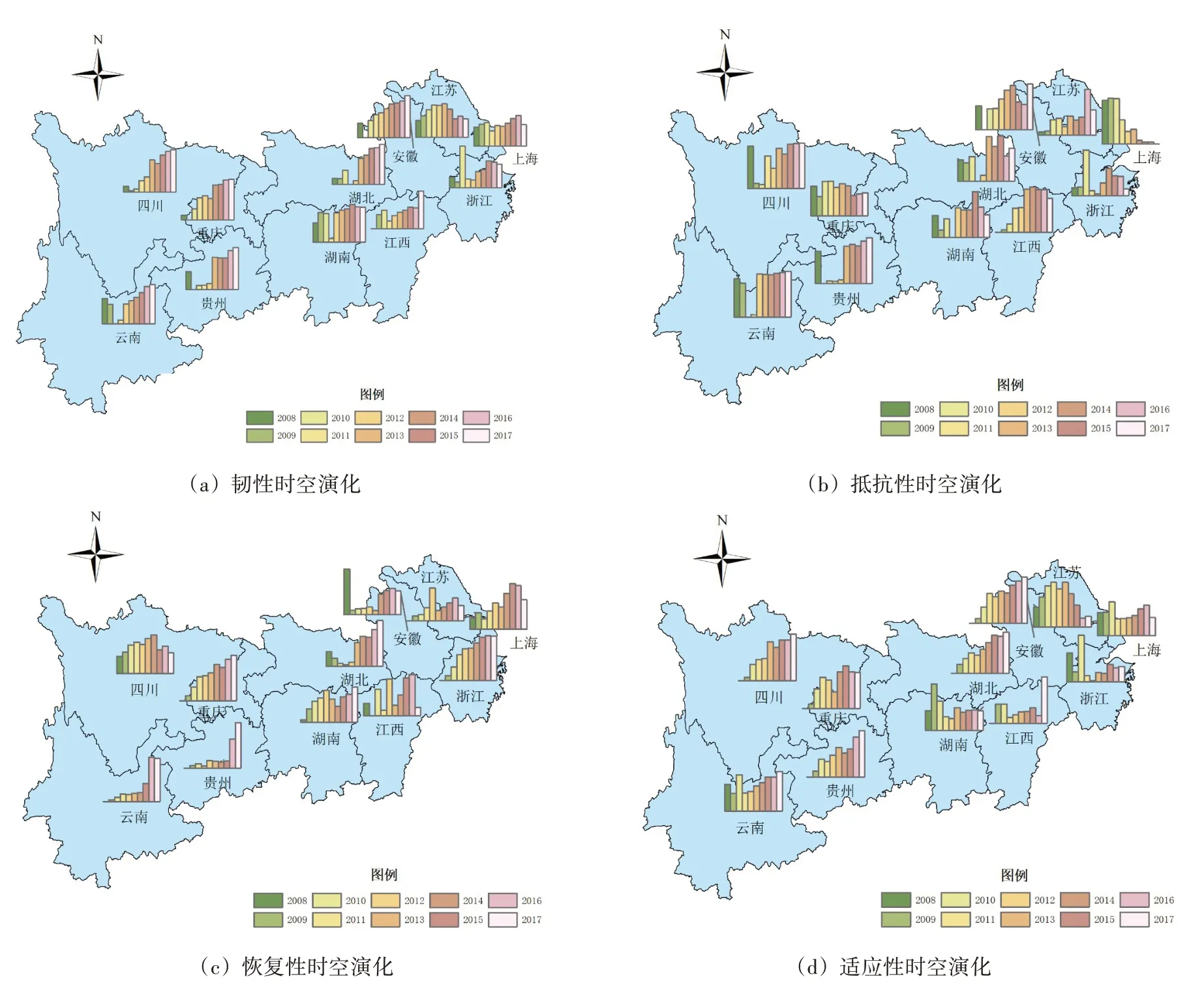
图3 长江经济带2008—2017年11省级行政区水资源系统韧性的时空演化

将长江经济带划分为东段（上海、江苏、浙江）、中段（安徽、江西、湖北、湖南）和西段（重庆、四川、云南、贵州），并从水资源系统韧性及抵抗性、恢复性和适应性等四个方面进行区域之间的横向对比，以期发现长江上中下游城市群的水资源韧性优势与短板。具体见图4。

根据图4（a），长江经济带2008—2017年的水资源系统韧性呈上升趋势；中西段韧性水平持续提升；东段相对稳定，无明显改善，且2013年以来，自身优势减弱，被中、西段超越。由图4（b）（c）（d）可以发现，东段的抵抗性明显弱于中、西两段；东、中、西三段的恢复性均为逐年提升的态势；适应性方面，东段区域近年来有一定程度的降低。

图4 长江经济带2008—2017年东、中、西水资源系统韧性横向比较

西段区域自然条件优越，水资源较为丰富，应进一步强化水源涵养、水土保持，合理开发利用水资源，促进水资源系统韧性；中段湖泊湿地众多，肩负着重要的调水功能，应加强协调江湖关系，保护水生生态系统，进一步优化和规范沿江产业发展，确保长江中游水资源系统韧性的稳步提升。东段区域人口密集，经济相对发达，工业化水平较高，产业同构化问题突出，水资源系统面临着巨大的压力，应进一步优化产业结构，提升用水效率，实现水资源的高效利用与可持续发展。

为精准挖掘韧性的重点调控指标，以2017年研究单元，对18项指标分别进行排序，进而对折衷韧性排序值进行异常检测（设θ=0.5），挖掘主要调控指标。统计发现，在11 个省级行政区各指标的排序值中，“小于0.5”出现5 次以上的指标共有6 个，即工业用水、农业用水、生态环境用水量、环境治理投资、财政收入增率和科技研发投入。在这些指标上，长江经济带各省级行政区之间悬殊较大且低水平地区相对较多，因此这6项指标是总体韧性水平的主要扰动因子。具体见图5。

由图5可知，江苏、江西、安徽等省份的工业用水量较大，同时江苏、湖南和四川等省份的农业用水量较大，因此就产业结构而言，建议对江苏、江西、安徽等工业用水量大地区的旧动能、落后产能进行产业升级，对等农业用水量大的地区发掘节水潜力；就环境治理以及水生态保护而言，安徽、浙江、四川、江西等地区的生态环境用水量较大，而贵州、江西及湖北地区治理水平相对较弱，需着力加强水源地、水功能区保护，抓好生态保护；在财政和科技投入方面，重庆和云南等地区相对较为滞后，建议当地相关部门深入研判当地水资源系统的韧性现状，制定有效的调控方案，同时加大对科技研发的政策和资金支持，提升当地产能水平，促进水资源系统的韧性提升和可持续发展。此外，就防灾减灾水平而言，湖北、安徽、四川、云南、贵州受到干旱影响较大，江西、湖南、湖北等地受洪灾影响较大，应采取相关措施对该区域的洪涝灾害进行重点防治；各区域还需建立多层次数据共享平台，为水资源系统韧性提升提供支撑保障。

图5 长江经济带2017年各省区6项重点韧性调控指标的等级排序分布

4.5 模型检验在本节中，通过调整决策系数τ()0 ≤τ≤1 值，检验韧性水平排序的改变情况，实现模型的灵敏性分析，结果见图6。

图6 不同τ值情况下长江经济带2008—2017年水资源系统韧性排序

图6表明，决策系数τ的不同取值对应不同的排序，从而对所评价结果产生影响，但韧性水平最高的年份没有改变，始终是2015年。韧性水平最低的年份，在τ≤0.3时为2011年，在τ≥0.4时为2010年，这符合人们的决策偏好模式。事实上，决策系数τ反映了群体效用最大化和个体遗憾最少化之间的折衷。因此，τ的差异性取值显示了决策者的主观偏好在决策中的作用。

将本文的可变勾股模糊VIKOR 模型与传统勾股模糊VIKOR 方法的进行比较，结果表明可变勾股模糊VIKOR方法的优势体现在：（1）利用可变集相对隶属度方法确定勾股模糊数，将决策矩阵中的勾股模糊数由原先的离散取值拓展至较为连续的模式，更好地刻画了等级之间的模糊对立统一；（2）勾股模糊决策矩阵的确定不依赖于专家经验，由客观数据与等级标准之间的隶属关系确定，一定程度上克服了现有勾股模糊VIKOR 方法的主观性问题；（3）由图7可知，本文提出的可变勾股模糊VIKOR 方法与现有勾股模糊VIKOR 方法的决策结果基本一致，但在各年度上均存在一定的正向或负向的差异，较好地弥补了由相邻等级之间边界过于绝对造成的某些指标的不可分辨问题。

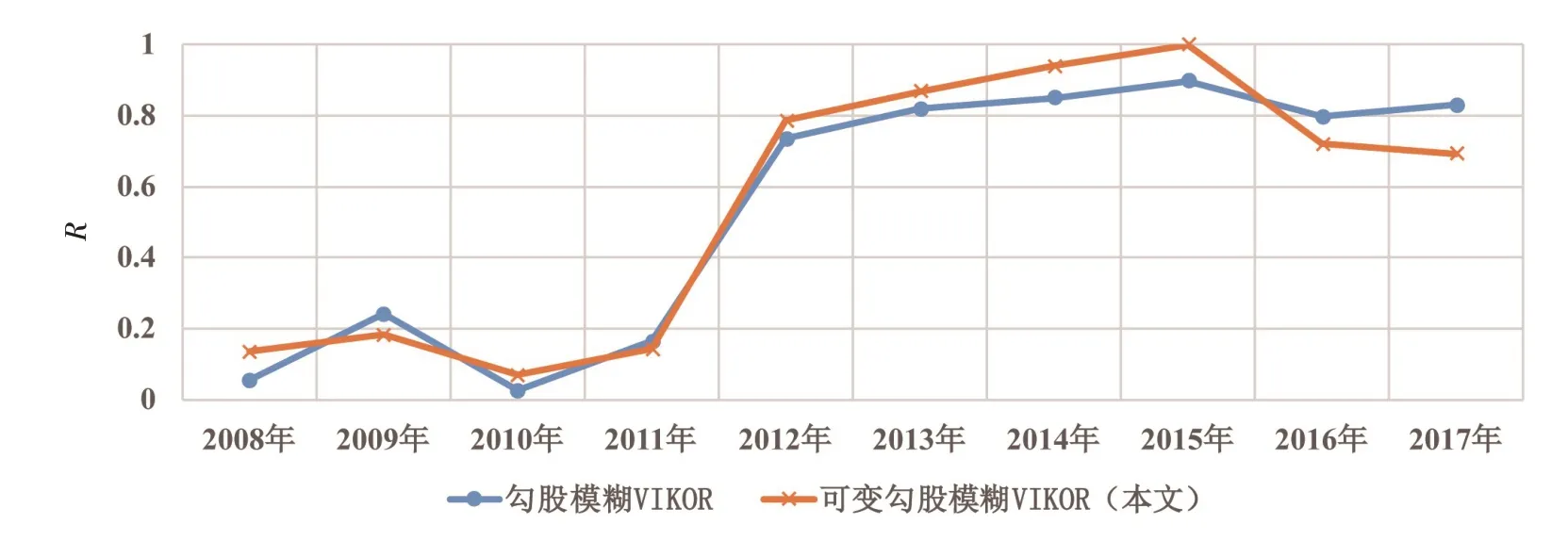
图7 本文方法与已有方法结果比较

5 结论

本研究提出了一种基于可变集和勾股模糊集的VIKOR 多指标决策模型，以期对水资源系统的韧性进行评价与调控。在该模型中，决策者的偏好仅在对群体效益和个体遗憾的折衷上有所体现，在一定程度上提升了勾股模糊VIKOR 模型的客观性。通过在长江经济带水资源韧性评价与调控中的应用，验证了可变勾股模糊VIKOR方法的适用性和可行性，并通过灵敏性分析，说明了不同决策系数τ的影响。此外，与现有勾股模糊VIKOR方法相比，本文提出的方法具有客观、连续等特点。

在水资源系统韧性的评价过程中，构建不同的指标体系可能会得到不同的评价结果，因此在评价结果的指示值上可能会存在一定的差异性，然而客观的水资源系统韧性状态及演化情况应基本趋于一致。本文依据科学性、合理性以及可获得性原则，从抵抗性、恢复性和适应性三个方面探索水资源系统韧性评估策略，构建了共含18 项指标的多级评价指标体系，以期较为全面地反映水资源系统的风险应对能力。研究结果表明，长江经济带2008—2017年水资源系统韧性总体上呈现逐年提升的态势。在2015年出现峰值，随后开始出现了一定程度的降低，其主要扰动因子在于适应性子系统，因此应通过调控适应性子系统的各项指标，实现水资源系统韧性的稳定提升。此外，长江经济带11个省区的水资源系统韧性具有时空分异特征。中西段韧性水平持续提升；东段相对稳定，无明显改善；东段的抵抗性明显弱于中、西两段；东段区域近年来适应性水平有一定程度的降低等。

由于水资源系统日益复杂，决策者很难将所有因素全部考虑，因此，采用可变勾股模糊VIKOR方法进行多指标决策，可以保证决策结果更加合理。勾股模糊集的其他重要研究途径是与前景理论、层次分析法和理想点法TOPSIS的耦合研究，可使得勾股模糊集在诸多领域更加适用。