基于ADAMS的无菌砖型包装机预成型机构动态仿真
何咸荣,潘 嘹,卢立新,林自东,厉夫满
(1.江南大学 机械工程学院,江苏无锡 214122;2.山东碧海包装材料有限公司,山东临沂 276600)
0 引言
无菌包装可减少食品在杀菌过程中营养成分和原有风味的损失,具有延长食品货架期等优点,其中纸塑铝复合材料包装占重要部分[1]。我国纸塑铝复合材料无菌包装市场巨大,但国内自主研制的无菌砖型包装机在生产速度、工作稳定性等方面与国外高水平同类装备还有差距。为此,开展设备动力学分析与优化成为研究重点之一。
目前国内外对无菌砖型包装机的研究关注点各有不同,如郭杰等[2]建立振动耦合方程通过MEWMARK-β法求解并分析影响预成型机构支撑杆振动响应规律的因素;杨振宇等[3]研究高速无菌灌装机对温度、压力、流量、机构运动等控制因素,设计以PLC为核心的多点控制系统;尚峰磊等[4]设计基于伺服驱动的预成型双滑块机构并用ADAMS进行仿真分析;石复习等[5]分析包装设备零件更换和工作条件历史数据,设计对设备零件剩余寿命预测的BP神经网络;CANOSA等[6]通过试验与仿真对比分析,建立可通过砖包机运行状态相关数据来评估各组件工作情况的虚拟样机模型;ARREOLA等[7]提出用于监测和评价过氧化氢气体在无菌灌装机中杀菌效果的组合生物传感器阵列。
无菌砖包机主要包括包材行进系统、杀菌系统、预成型系统、后成型系统等。其预成型系统中机构的工作稳定性直接影响砖包预成型质量。虚拟样机技术可对包装机械产品的设计进行有效检验[8-10],本文以预成型机构为研究对象,在ADAMS中通过对机构中凸轮与滚子分别设置几何相切约束与弹簧预压接触约束得到各个零件的运动学与动力学特性,对比分析机构动态失稳的原因,为预成型机构运动规律研究与结构参数优化提供有效依据。
1 预成型机构工作原理
预成型机构三维简图如图1所示。该机构由两相同结构的凸轮连杆组合机构组成。机构运动时外凸轮与滚子接触并且驱动下摆臂,下摆臂与固定块铰接并控制外立轴竖直方向的运动;内凸轮驱动上摆臂绕定点摆动,上摆臂控制内立轴在竖直方向的运动;下支撑件、固定轴套和轭架组成双滑块并联机构,下支撑件与内立轴刚性连接,固定轴套与外立轴刚性连接,两立轴带动轭架转动以及竖直方向的位移以控制执行机构末端的运动而实现砖包机预成型功能。
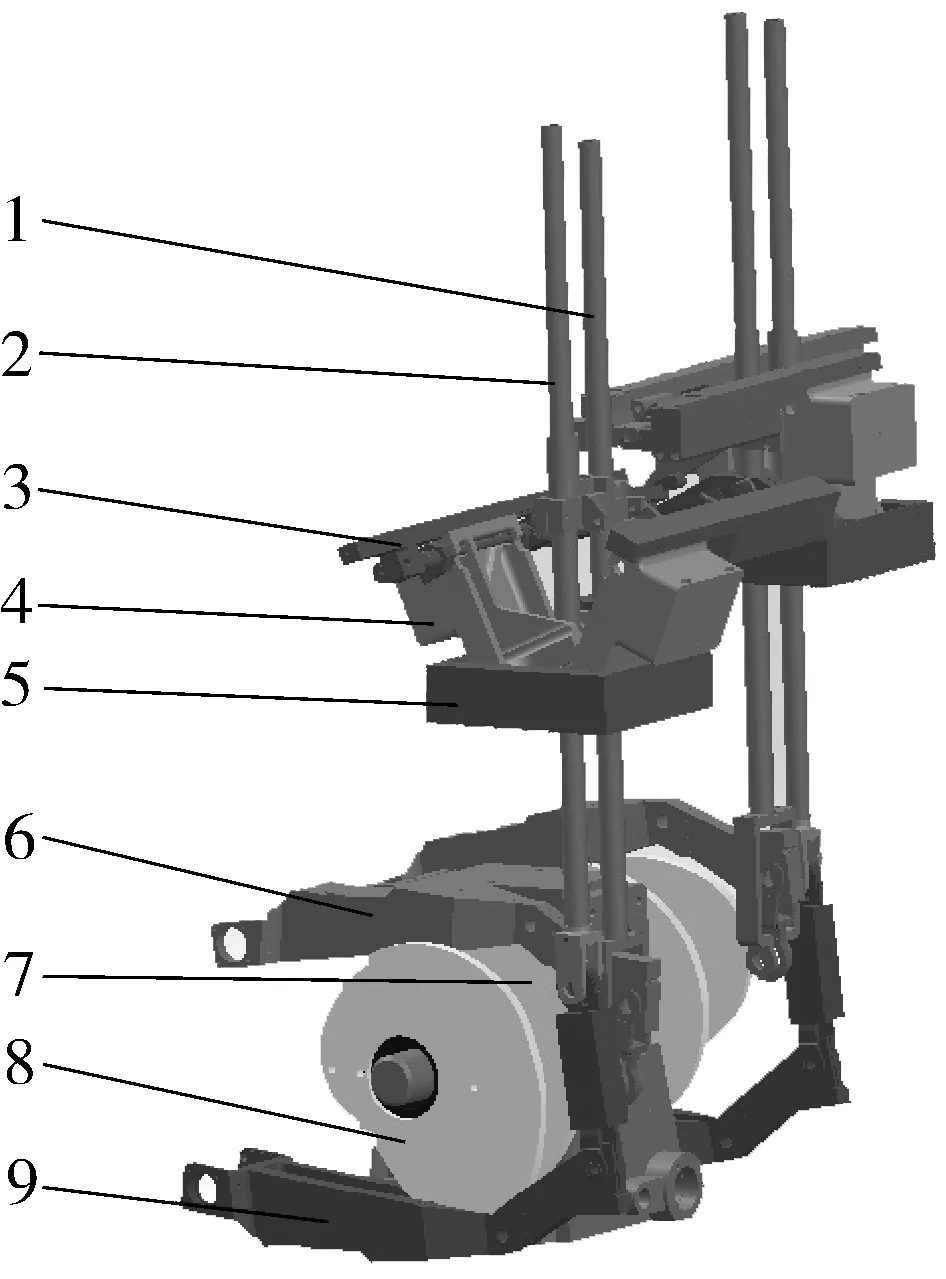
图1 预成型机构三维简图Fig.1 Three-dimensional diagram of preforming mechanism
运动过程中当一对夹爪拉动包材下移时,另一对夹爪沿竖直方向下移并闭合,两对夹爪都闭合后按先等速后差速的规则运动,更低位置夹爪的内置刀片切割包材并完成出包,最后夹爪空载回程完成一个周期运动,两对夹爪以往复开合的形式实现纸盒横封-折角压包-横切出包的复杂动作。
2 预成型机构动力学等效模型建立
在预成型机构实际运行中,其构件会发生的弹性变形会对整个机构的运动产生影响,建立动力学模型是研究机构动态特性一种有效方法。实际工程中,预成型机构中的凸轮-从动件系统可简化为单自由度或双自由度模型。根据零件变形势能守恒建立动力学等效模型,简化模型如图2所示。
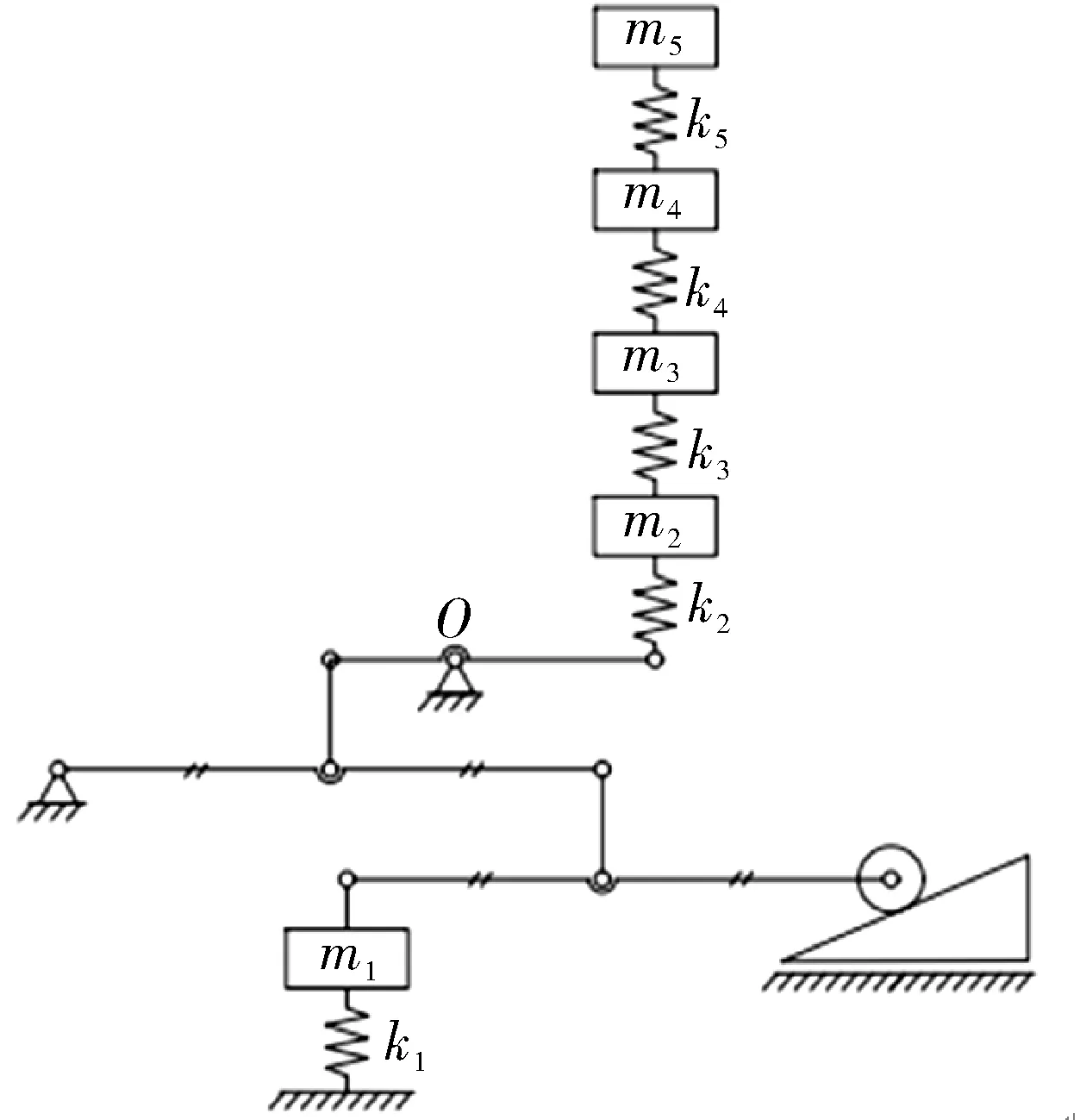
图2 等效简化模型图Fig.2 Simplified diagram of equivalent model
零件质量按集中质量等效,等效刚度以零件弹性变形势能守恒为原则进行代替。图中凸轮的等效质量为m1,轴的等效刚度为k1;k2、m2分别为摆臂的等效刚度和质量;k3、m3分别为摆臂连杆的等效刚度和质量;k4、m4分别为立轴的等效刚度和质量;k5、m5分别为夹爪的等效刚度和质量。
通过等效质量和等效刚度的转移将弹簧锁合型的凸轮-从动系统转化为单自由度系统。由牛顿第二运动定律建立动力学方程:
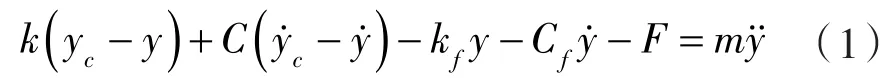
式中 k——等效刚度,N/mm;
m——等效质量,kg;
F——锁合弹簧预紧力与工作载荷的合力,N;
kf——锁合弹簧刚度,N/mm;
yc——激励当量运动位移参数,mm;
y——工作端实际位移,mm;
C——系统阻尼,N·s/m;
Cf——锁合弹簧阻尼,N·s/m。
为说明摆臂运动规律对夹爪响应的影响,略去系统阻尼 C、Cf[11],则动力学方程可改写为:

根据构件等效替代原则有:

式中 LOA,LOB——凸轮到轴两端的距离。
3 虚拟样机模型动力学仿真分析
3.1 模型简化与导入
导入两对结构相同的凸轮连杆组件的一对进行仿真分析。首先在Solidworks中分别对摆臂、夹爪等零件模型进行布尔操作以减少倒角、结构间隙等影响求解速度的因素,然后保存为相应格式并导入ADAMS。
3.2 材料属性设置
为提高仿真结果精确性,设置仿真模型材料属性与样机材料属性一致,各零部件材料属性见表1。
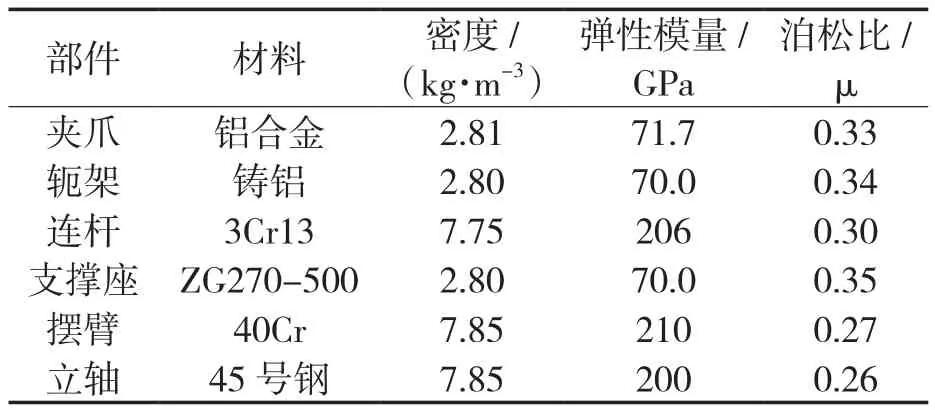
表1 各零件材料属性Tab.1 Material properties of each part
3.3 凸轮与滚子的两种约束定义
当预成型机构中凸轮的运转速度较高时,机械系统中运动构件的惯性力剧增会导致机构运动失稳,分别采用几何相切约束与弹簧预压接触约束定义凸轮与滚子的连接来分析机构运动失稳的原因,其他部件约束定义设置相同。凸轮滚子间使用Curve-Curve持续接触类型以保证滚子与凸轮不可分离;而实际约束下摆臂通过弹簧压力复位,因此在凸轮与滚子间设置Solid-Solid时断时续接触来模拟实际约束,在normal force选择Impact接触法计算接触力;其中设置弹簧副刚度为10.5 N/mm,设置弹簧预压力为800 N。
3.4 预成型机构仿真与结果分析
根据凸轮实际转速在凸轮轴心添旋转驱动并设置驱动函数-374.4 d*time。最后对模型系统进行验证,查看系统自由度、干涉等情况继而确保仿真的正确性。夹爪初始位置处于夹爪张开空载回程,在Simulation control对话框中将运动时间设置为1 s,步数设置为300。在Professor模块中对预成型机构的工作端进行位移、速度、加速度等参数测量并获取相应曲线。
摆臂角位移与立轴位移变化曲线如图3所示。摆臂随时间变化的角位移与立轴随时间变化的位移存在数值关系,而预成型机构复杂的动作是通过凸轮控制,这说明可通过摆臂角位移与夹爪角位移的变化来分析不同凸轮曲线对应夹爪的运动状态。

图3 摆臂角位移与立轴位移变化曲线Fig.3 Curves of angular displacement of swing arm and vertical axis displacement
图4(a)为几何相切约束下摆臂角位移与夹爪角度变化曲线,0.0~0.06 s内执行机构处于空载回程位置处并且夹爪张开角度持续增大,但此时两个夹爪已不会再发生干涉,即此阶段夹爪运动角度冗余;在0.25~0.76 s,夹爪角度基本不变,但在此阶段末端即出包时角度存在幅度较小波动,当驱动凸轮转速继续提升可能导致包装盒输出位置不稳定,从而使预成型纸盒受不同程度的冲击;0.76~1.0 s期间,夹爪处于快速空载回程阶段,摆臂角位移较平缓,运动较稳定。
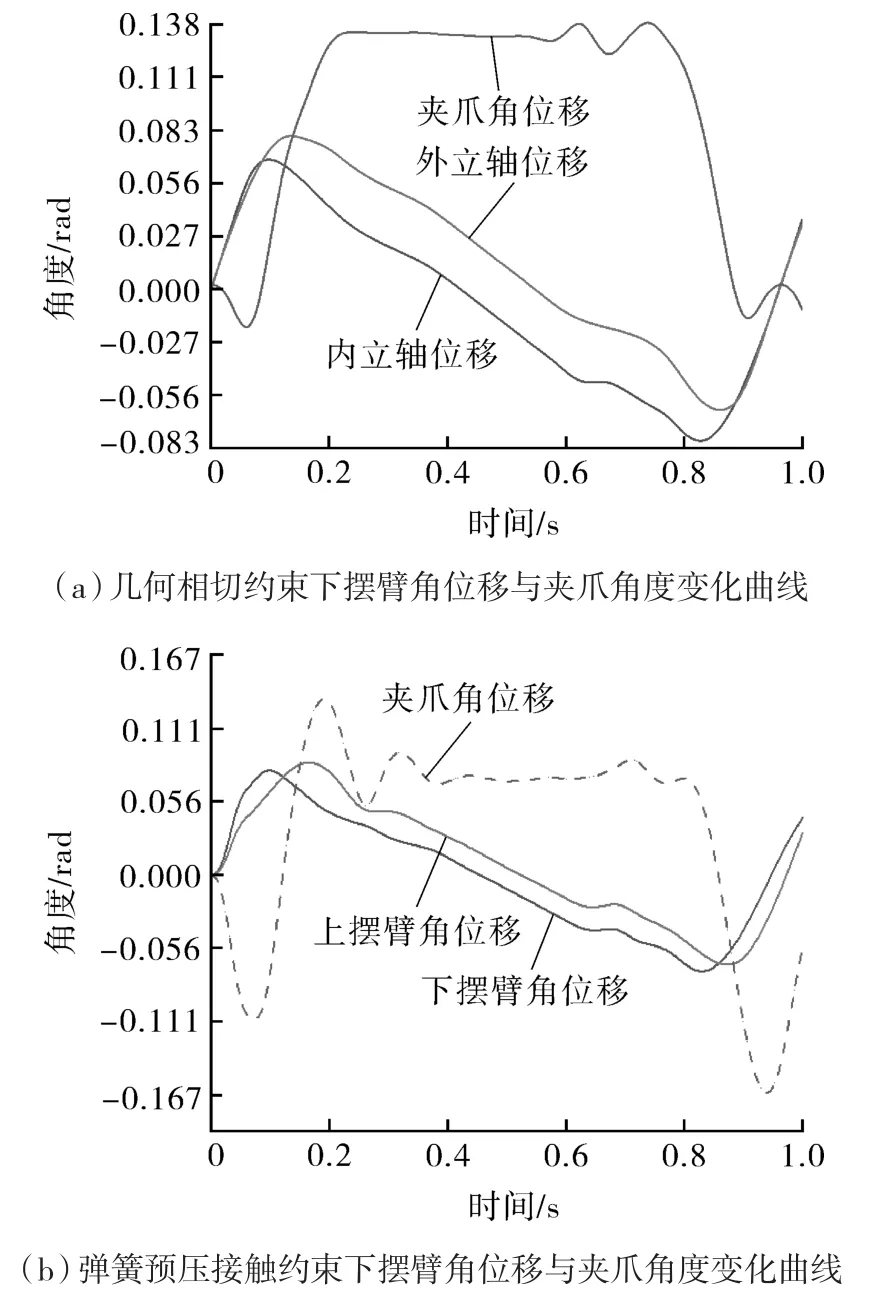
图4 两种约束下摆臂角位移与夹爪角度变化曲线Fig.4 Curves of the angular displacement of the swing arms and the angle of the gripper under two constraints
图4(b)为实际摇臂角度的变化以及对应夹爪角位移变化曲线,0.0~0.2 s内下摆臂对应凸轮轮廓的回程阶段,而弹簧预压接触下滚子与凸轮存在的微小间隙会导致摆臂的角位移相对理论角位移滞后0.01;而上摆臂此时间内对应凸轮轮廓的推程阶段,角位移曲线表明运动过程中滚子与凸轮存在跳腾,这导致瞬时高副失效从而引起机构运动失稳。两摆臂的运动误差共同导致夹爪的角位移大于几何相切约束下的角位移,进包位置处夹爪更大的角位移变化会增加夹爪闭合时的冲击,影响预热封位置精度与可靠性。0.2~0.8 s内夹爪角位移微小波动可能由摆臂上弹簧刚度不足或零件质量过大引起,因此部件结构参数对砖包预成型工艺可靠性有影响;0.8~1.0 s内,下摆臂的角位移与理论相似,但上摆臂的角位移存在滞后,这由凸轮轮廓曲率变化过大和在上摆臂上施加的弹簧力不足共同导致。
图5为滚子与凸轮接触力的变化曲线,0.04 s处下摆臂上的滚子与凸轮的接触力开始急剧减小又瞬速增大,此处高副失效时间很短,对夹爪轨迹影响很小;0.1~0.2 s滚子跳腾持续约0.04 s,使得夹爪在相撞时角位移产生较大的波动,接触力为0 N处,高副失效的具体位置。上摆臂滚子0.03s附近出现短时跳动,其他时间内均保持与凸轮的接触。上下摆臂出现不同程度的滚子腾跳,但下摆臂的运动相对更加不稳定对砖包预成型质量更为不利。

图5 滚子与凸轮接触力变化曲线Fig.5 Change curve of roller and cam contact force
图6(a)为摆臂的理论角加速度曲线,分别在0.1 s、0.9 s处,凸轮轮廓曲线对应运动规律变化导致摆臂存在幅度较大的角加速度变化,较高频率的加速度突变导致机构动态稳定性降低,滚子对凸轮造成较大柔性冲击也是导致运动失稳的原因,为避免冲击引起系统有害振动,需严格控制凸轮与滚子的间隙量,凸轮轮廓曲线仍需改进或者对接触元素施加足够的预压力。根据图6(b),0.2~0.8 s内摆臂加速度呈现较小的波动是运动规律变化导致的残余振动,在出包阶段摆臂角加速度呈现出比理论值更小的变化,弹簧接触约束下出包更稳定。
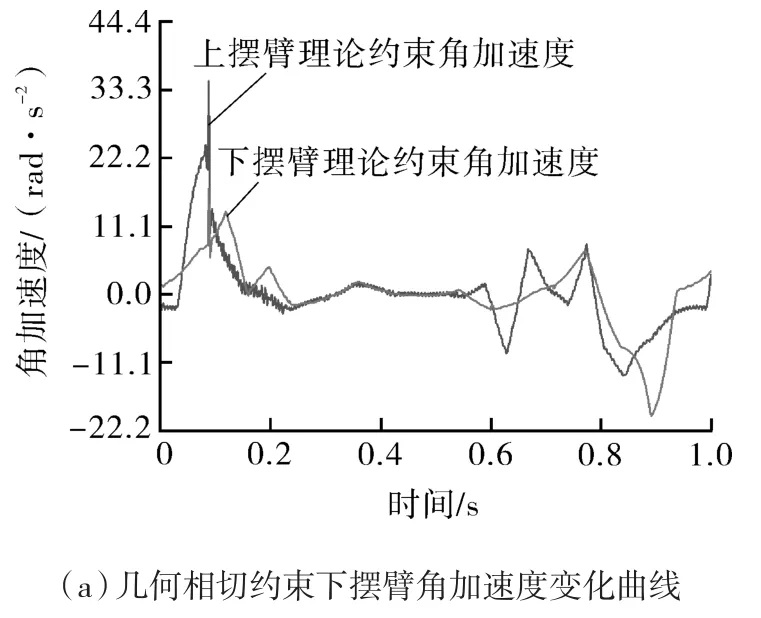
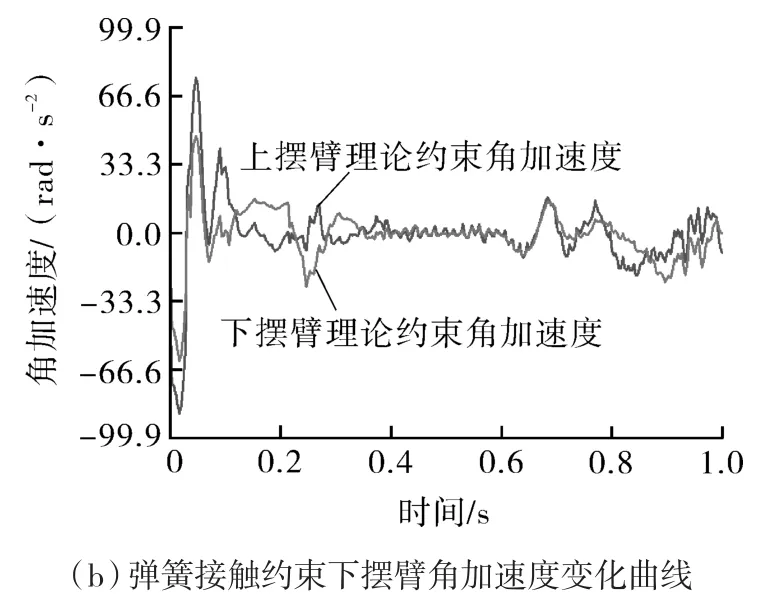
图6 两种约束下摆臂角加速度变化曲线Fig.6 Angular acceleration curve of the swing arm under two types of constraints
4 结语
本文先建立无菌砖包机预成型机构动力学模型,通过Adams仿真对预成型机构的运动学与动力学分析。结果表明,在高速运转时进包和出包位置出现运动失稳主要原因是瞬时高副失效,滚子跳腾会随着转速提高而增加。为保证机构运动稳定性需进一步改进凸轮轮廓曲线或增加弹簧预压力,从而减小凸轮与滚子间的柔性冲击。应用虚拟样机技术发现无菌砖型包装机预成型机构在运行时存在的问题与缺陷,为后续预成型机构运动规律优化提供有效依据。

