基于RD-PSO优化算法的自适应数据流分类

邹劲松 李 芳

1(重庆水利电力职业技术学院普天大数据产业学院 重庆 402160) 2(重庆大学计算机学院 重庆 400044)

0 引 言

由于无处不在的互联网和激增的移动设备，各种来源的数据流数量指数级增长，这样的流通常以高速和数据分布随时间的变化为特征[1]，非平稳数据流分类在机器学习和数据挖掘领域的重要性与日俱增。概念漂移分为多种类型，如突变式、渐进式和重现式等[2]。其中：突发式概念漂移指数据的分布突然被新的分布所取代；渐进式概念漂移是指传入数据的新分布比例会提高，而来自前一分布的数据的比例会随着时间的推移而下降；重现式概念漂移指相同的旧数据分布在经过一段时间后以不同的分布重新出现[3-4]。比较理想的非平稳数据流分类方法应能够在最小化计算复杂度的同时具有最小可能的误分类率，并可以快速适应可能的概念漂移。

集成学习技术使用投票机制创建并组合多个分类器，以建立单个类作为数据实例的输出[5-6]。由于其在训练和更新分类器方面的灵活性，集成技术对非平稳环境中的流分类有较好的性能。粒子群优化(Particle Swarm Optimisation, PSO)算法是通过模拟鸟群或鱼群中觅食行为而发展起来的一种基于群体协作的随机搜索算法[7-8]，它的主要目标是找到函数的全局最小值。PSO通过创建候选解的初始随机群来进行初始化，然后粒子以动态速度在搜索空间中适应性移动以找到最佳解决方案[9-10]。

近年来，有关非平稳数据流分类已取得若干成果。文献[11]提出了一种基于增量式半监督模糊聚类算法的数据流分类方法，用来处理不同类型的数据。它创建与类数量相同的群集，但是固定数量的群集可能无法充分捕获流数据的演变结构。文献[12]提出了基于规则的多标签分类方法和基于连续数据流的集成学习方法，该方法基于目标回归算法将类标签子集的规则专门化，而不是通常的局部(每个输出的单个模型)或全局(所有输出的一个模型)方法。文献[13]提出了一种用于进化数据流分类的自适应随机森林(Adaptive Random Forest, ARF)算法，它通过在原始数据的重新采样版本上对决策树进行训练和随机选择少量可在每个节点处检查以进行拆分的特征来生成决策树。该方法是一种使用机制检测概念漂移并立即作出反应的显式方法，其最大缺点在于对噪声比较敏感，导致准确性会因为错误检测到概念漂移而降低。

在研究了现有数据流分类的基础上，为了有效地适应最新的数据分布类型，本文提出一种基于复制动力学和粒子群优化(RD-PSO)的自适应数据流分类技术，RD-PSO通过从目标数据集的属性集合中随机选择特征生成三个不同分类类型的分类器集合，通过将复制动力学(Replicator Dynamics, RD)应用于集合的所有层来使所选择集合的每一层需要的分类类型的数量随着层中每种分类类型中的特征数量的增加而减少，从而实现无缝适应最新数据分布类型的目的，使用粒子群优化技术的非规范版本来确保快速适应不同的概念漂移。

1 基于RD-PSO的数据流分类

RD-PSO算法通过从目标数据集的属性集合中随机选择特征(子空间)生成的不同分类类型的三层次分类器集合，应用RD-PSO算法来优化所有层，以此来无缝且有效地适应最新的数据分布类型。

图1给出了三层的RD-PSO算法的示意图。左边三角形表示分类类型的范围及它们在每一层中所覆盖的特征，直角三角形表示每种分类类型向全局和局部最优移动的速度，分类类型越小(特征越少)，它们向最优方向移动的速度越快。

图1 三层RD-PSO算法描述

1.1 创建分层

本文算法使用每个层中特征的随机子空间创建三个不同的包含特定数量类型的层，每个分类类型覆盖来自预定义特征池的特定百分比的特征，每种类型中特征的百分比与每层中的类型数之间呈负线性相关。换言之，每种类型在同一层中需要覆盖的要素数量随着每一层内的类型数量的变大而减小，即：

(1)

式中：m表示类型的总数；n表示要为每种类型选择的特征总数；f表示目标数据流的特征总数。

每个层的参数一旦被指定，就从所有属性的集合中随机选择nl个特征(属性)，此步骤对每层重复ml次，l表示层号(l=1,2,3)。因此，在此步骤结束时每层都有ml个独立的类型。

1.2 复制动力学

对所创建集合的每一层，应用复制动力学(RD)选择每层中的分类类型和特征的数量，使得该层需要的分类类型的数量随着层中每种分类类型的特征数量的增高而降低。

(1) RD概述。RD是选择过程的显性模型，它将表现好于平均收益的类型规模增加，而那些表现比平均收益差的类型规模减少。该模型在离散时间进行选择，下一次选择中的每种类型群体作为该类型的收益及其在群体中的当前比例的函数，由式(2)给出。

(2)

式中：W表示游戏的正常形式的支付矩阵；(Wx)i表示个人的预期收益；xTWx表示人口状态x的平均收益。

在所设计的方法中，分类类型是目标数据流的特征总数的随机子空间，一种类型的收益是同一类型内部分类器的平均精度，而预期收益是所有现有分类器的平均精度。

(2) 初始训练。所有层被创建后，集合使用RD开始训练数据。在原始RD中，需要添加到子空间的树的数量分别为：

(3)

(4)

式中：Ta(i)表示要添加的树的数量；Tr(i)表示要移除的树的数量；a(ti)表示正在处理的子空间i的精度；m表示类型的总数；Tn(i)表示当前在子空间i内的树的总数。

当添加到子空间的树的数量大于1时，将使用引导聚合模型创建不同的树，此时输入数据用于测试和训练，而不能进行先验评估，因为在每个时间步骤中只能创建一棵树，但是因为投票目的给它分配更高的权重，因此权重为2的树在投票机制中有更高的影响。该策略中的移除机制基于分类器的性能，例如，当移除的树的数量为2时，在最后的数据块里从集合中移除两个最不准确的树。

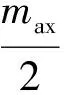
(3) 投票阶段。多数投票通过式(5)获得的权重来组合每一层的输出从而确定集合的输出。

Wi=Wi-1+α(Pi-1-Ai-1)

(5)

式中：Wi-1表示第(i-1)个数据块上的层的权重；Pi-1表示第(i-1)个数据块上同一层的精度；Ai-1表示第(i-1)个数据块上所有层的平均精度；α表示最近数据的系数，该系数是本文算法的任意参数(α>1)。

(4) 评估阶段。评估阶段通过计算其准确性对每个类型的决策树进行评估以对输入实例进行分类，每种类型的精确度是其组成决策树的平均精确度，整个集合的精确度可以用式(6)来确定。

(6)

式中：ci表示第i个数据块中正确分类的实例数量；db表示每个数据块中的实例总数。

式中：a(ti)表示第i种类型的精度；m表示类型的总数；grow表示添加新的分类器/类型；shrink表示去除性能差的分类器/类型。本文预期收益被设置为每一层中所有类型的平均精确度。

为了设置框架内分类器(决策树)数量的边界，为集合中的所有类型设置了max=10的任意上限，一旦超过了一种类型分类器的数量，就会移除相同类型的性能最差的决策树，从而为新构建的分类器腾出空间。为了防止类型被完全删除，将min=1作为下限分配给所有类型。

1.3 粒子群优化

粒子群优化通过创建候选解的初始随机群来进行初始化，然后粒子以动态速度在搜索空间中移动以找到最佳解决方案。粒子的运动由称为先前最佳(previous best, pbest)和全局最佳(global best, gbest)这两个极值来更新自己，pbest位置是整个历史中粒子本身的最优解，gbest位置是整个群体中所有粒子的最优解，在每次迭代时重复该过程以便发现令人满意的解决方案。粒子的速度(V)和位置(P)分别根据式(9)和式(10)更新。

Vi(t+1)=ωVi(t)+r1(pbest(i,t)-Pi(t))+r2(gbest(t)-Pi(t))

(9)

Pi(t+1)=Pi(t)+Vi(t+1)

(10)

式中：ω表示用于平衡全局和局部开发的惯性权重；r1和r2为加速度系数。

典型的PSO由于针对静态数据进行迭代导致只有一个可能的最优解。在数据流分类任务中数据以在线方式出现，最优解会随着时间而变化，因此本文使用非规范化的PSO来优化每层内部类型特征的组合。PSO将所有随机创建的类型作为其输入，并尝试在每次迭代(接收到新的数据块时)中以指定的速度将它们移动到全局最优和局部最优解决方案类型。“将粒子以一定速度移动到特定空间”是指将粒子特征的组合进行重组，使其类似于具有速度的特定特征子空间。

在本文算法中，对于第3层、第2层和第1层，常数β的值分别被任意分配为1、0.7和0.4，因此在每种类型中具有最少特征数的第3层中的最大速度被设置为100%，类似地，第2层和第1层的最大速度分别设置为70%和40%。

PSO在本文算法的每一层中单独执行，并在集合接收的每个数据块中迭代。结果集合的每一层内的粒子(类型)以指定的速度向同一层的全局最优和局部最优移动，该速度是基于它们在最后一个数据块上的性能计算的，其中它们的真实标签是已知的。注意，PSO的每次迭代仅在RD处理相同的数据块之后才开始。

2 实验与结果分析

为了验证本文算法的性能，本文在Intel Core i7-4702MQ CPU @2.20 GHz和8 GB RAM的机器上进行实验，所有测试均在大规模在线分析(Massive Online Analysis, MOA)平台上实现，MOA是一个基于WEKA用Java实现的数据流在线分类、聚类平台。选取模拟概念随时间漂移的合成数据流生成器SEA进行实验，SEA可以在三维空间生成随机点。数据块中的实例数为1 000，每个分类类型中分类器的数量为1到10，第1层到第3层的初始权重分别为1、2和4，最大速度阈值为x=2%。

图2给出了本文算法与自适应随机森林(ARF)算法[13]、动态加权多数(DWM)算法和OSBoost算法在所有数据集的即时和延迟设置中的总体平均精度。即时设置是指使用优先评估技术通过特定方法将所选数据集通过特定方法传递并立即访问实例的真实标签；延迟设置是指实例的真实标签在指定的延迟后显示给整体，本文延迟参数设置为1 000，即在传递1 000个实例后每个实例的实际标签都会显示给系统。

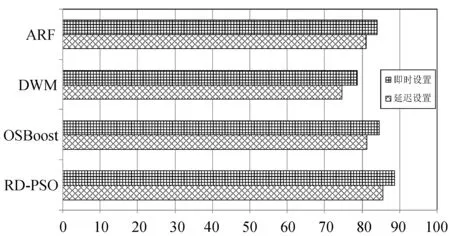
图2 各算法在即时和延迟设置中的总体平均准确度

可以看出本文算法在两种设置中都具有最佳的平均准确度，这是因为本文算法针对不同的环境和概念漂移采用不同的策略和使用不同的PSO优化层及其动态权重。

表1给出了各算法在即时设置中的评估时间。由于延迟设置中的评估时间类似于即时设置，本文仅给出即时设置的结果。可以看出，本文方法的总体评估时间不是最优，这是由于集合中分类器的数量随着目标数据流中的特征数量而增加，这些限制可以通过应用并行化独立处理来克服，这是未来研究的内容。

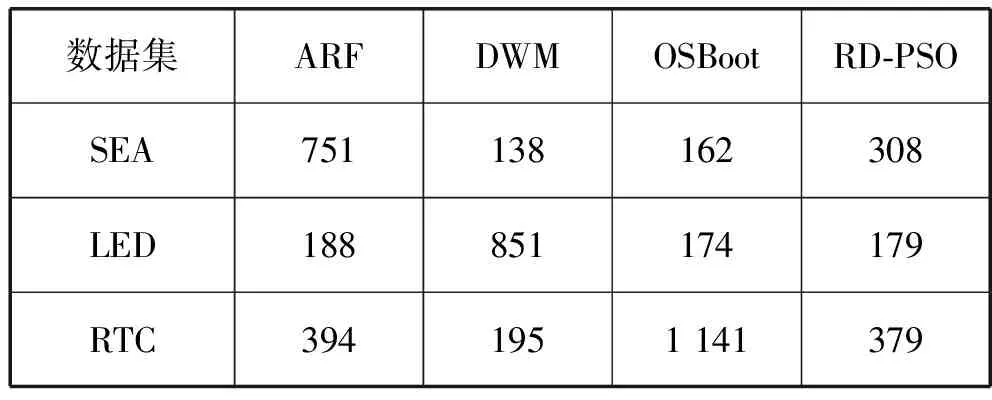
表1 即使设置中各算法的评估时间 s

图3到图6将不同类型的概念漂移添加到由SEA数据流生成器生成的数据集。其中：图3给出了本文算法与ARF算法、DWM算法和OSBoost算法在实例编号200k添加宽度为1的突变式漂移的适应情况；图4给出了各算法以10k的宽度添加渐变式漂移的适应情况；图5给出了各算法在实例编号600k处添加宽度为1的重现式漂移的适应情况；图6给出了各算法在实例编号为795k时以10k的宽度添加重现渐变式漂移的适应情况。

图3 各算法在实例编号200k时宽度为1的突变式漂移

图4 各算法以10k的宽度添加渐变式漂移

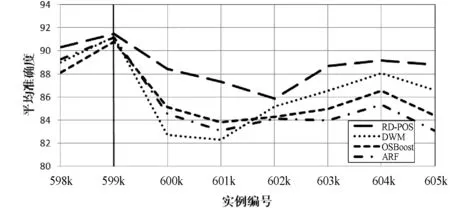
图5 各算法在实例编号600k处宽度为1k的重现式漂移

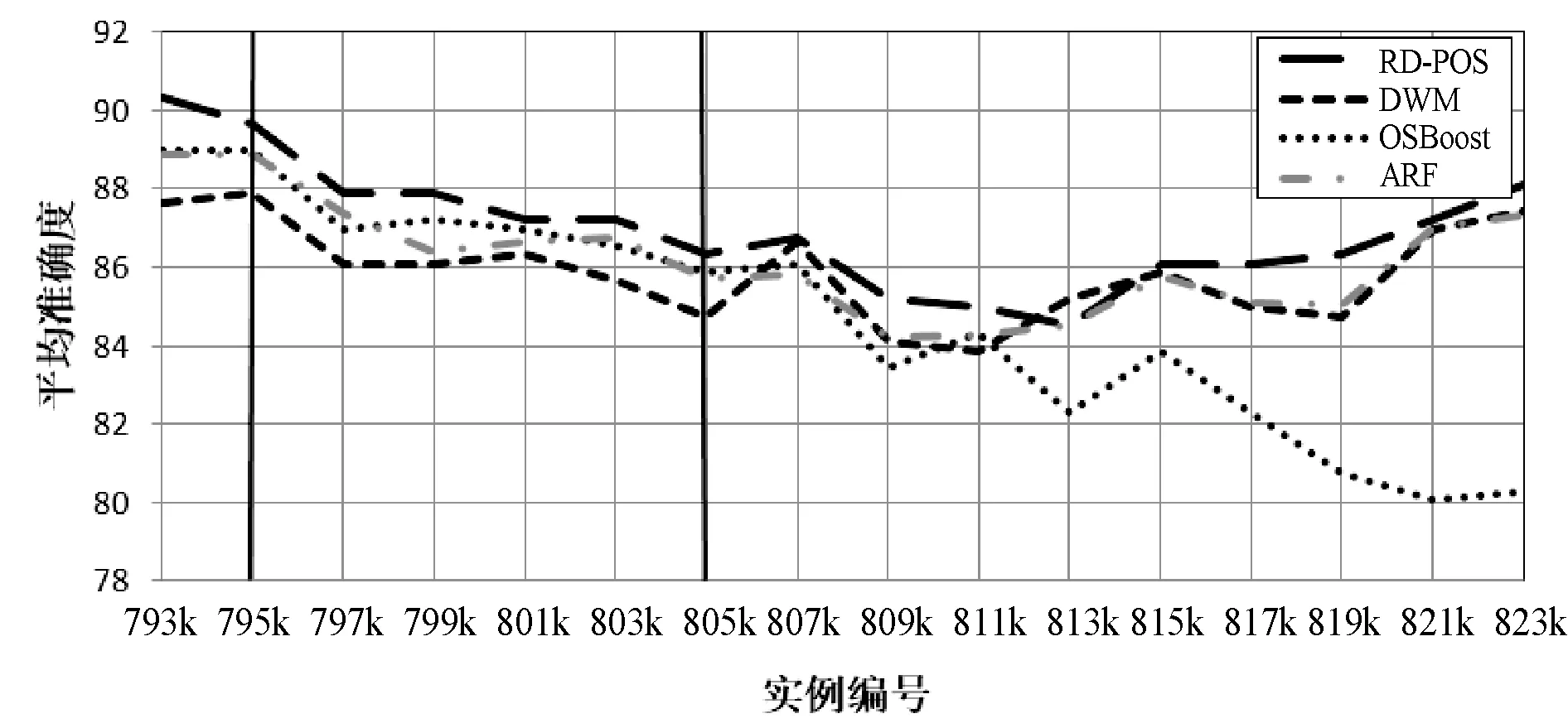
图6 各算法在实例编号795k处宽度为10k的重现渐变式漂移

可以看出，本文算法在突变式漂移和渐变式漂移以及重现式漂移中均可以快速地恢复，并且具有最高的精确度。这是因为本文算法使用改进的RD来无缝地不同的概念漂移，使用PSO技术的非规范版本对每一层进行优化，使每一层中的类型以指定的速度走向局部最优和全局最优。因此，本文算法比DWM和OSBoot有更好的准确性和鲁棒性。

3 结 语

为了使数据挖掘和优化技术适应概念漂移，本文提出一种基于复制动力学和粒子群优化的自适应数据流分类技术。该技术基于三层体系结构创建不同大小的分类类型，不同的分类类型通过从目标数据流的特征池中随机选择一定百分比的特征来创建，使用改进的RD通过增加表现好的类型规模和减少表现差类型的树的规模来无缝地适应不同的概念漂移，所有分类类型中的所选特征组合分别使用粒子群优化技术的非规范版本对每一层进行优化，使每一层中的类型以指定的速度走向局部最优和全局最优。实验表明，本文算法在准确性和鲁棒性方面均优于现有方法，但其总体评估时间不是最优。未来的工作是并行化独立操作的优化层来处理具有大量特征的目标数据流以减少评估时间，并设计一种方法来选择动态使用最大允许速度的阈值参数。