基于改进损耗分离模型的铁磁材料 损耗特性研究

赵志刚 徐 曼 胡鑫剑

（1. 省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学） 天津 300132 2. 河北工业大学河北省电磁场与电器可靠性重点实验室 天津 300132）

0 引言

随着电力电子技术的快速发展，电力变压器的应用越来越广泛[1-3]。变压器作为电力电子变换器的重要元件[4-5]，主要由绕组、铁心、绝缘装置等部分构成，其中，铁心通常采用铁磁材料叠压制成，为变压器提供磁回路。当铁磁材料工作于变化的磁场中时，将会产生磁损耗，并且工作于不同的谐波激励工况下，铁磁材料的磁性能也存在很大的差 异[6-8]，因此对于变压器设计者来说，研究变压器铁心铁磁材料的损耗特性，实现铁损的准确预测，是变压器优化设计的基础和必要环节[9-10]。

在实际的运行过程中，由于铁磁材料等非线性元件的使用，磁感应强度与磁场强度之间不再是线性关系，变压器激励信号也很少会是正弦波，这对变压器损耗模型的研究提出了新的要求[11]。值得注意的是，传统的损耗模型大多是基于正弦激励这一假设前提建立的，若用于计算谐波条件下的铁损，往往会出现较大的误差，模型的适用性降低。因此，如何实现谐波激励条件下损耗的准确计算受到了学者们的广泛关注，相关的研究文献也不胜枚举。

Bertotti损耗分离模型因物理意义明确，计算过程简单，被广泛应用于铁损的计算中[12-15]。随着损耗研究的发展，国内外学者在经典的Bertotti损耗分离模型基础之上进行了大量的改进，文献[16]基于损耗分离模型，考虑了静态、动态磁滞回线的区别，采用磁通密度多项式表征磁滞、剩余损耗系数，将高频高磁通密度条件下损耗计算误差降低到10%左右，但是该方法引入较多的未知参数，并且参数的辨析过程相当复杂。文献[17]基于损耗分离模型，建立了物理意义明确的动态Energetic模型，实现了正弦条件下铁磁材料磁滞回线的准确模拟，然而当磁滞回线中存在局部磁滞回环时该方法的有效性有待进一步验证。华中科技大学陈林认为，低频条件下，Bertotti损耗分离模型中的系数一般是恒定的，并基于常系数损耗模型实现了铁氧体材料损耗的准确计算[18]；然而D. M. Ionel等在其研究中指出，相比于常系数损耗模型，变系数模型具有计算精度更高、适用范围更广的优点[19]。文献[20]中，D. Eggers等考虑了趋肤效应以及材料非线性行为对铁损的影响，提出能够准确计算铁磁材料损耗的4参数表达式，但该模型不能用于谐波激励条件下损耗的计算。

为解决上述研究方法存在的问题，文中针对变压器铁心的铁磁材料——取向硅钢片B30P105的损耗特性展开研究，并基于损耗分离理论提出一种能够考虑材料非线性特征的铁损计算方法，实现了正弦及谐波条件下损耗的准确计算。

1 铁磁材料磁性能测试系统的搭建

1.1 实验测量装置

磁性能测试系统主要由激励源、测量电路、测量仪器三部分构成，其原理如图1所示。其中，激励源由信号发生器WF1974、功率放大器NF4520A构成，输出实验所需激励；测量电路由爱泼斯坦方圈构成，实验前，将称重后的24片牌号为B30P105的取向硅钢片依次搭接插入方圈的四边，构成磁回路，并在搭接处施加一定的压力，避免因空气漏磁通过大而增加测量结果的误差，表1为取向硅钢片B30P105的性能参数；测量仪器由功率分析仪LMG500构成，实验时缓慢调节信号发生器旋钮，注视功率分析仪示数调节到事先计算好的电压值，采集实验测量数据。

表1 取向硅钢片B30P105的性能参数Tab.1 Performance parameters of grain oriented silicon steel sheets B30P105

图1 磁性能测试系统原理Fig.1 Schematic diagram of magnetic performance testing system

1.2 激励的控制方法

实验时采用上述搭建的磁性能测试系统，通过 调节励磁电压的输出，控制铁磁材料上的磁通密 度为

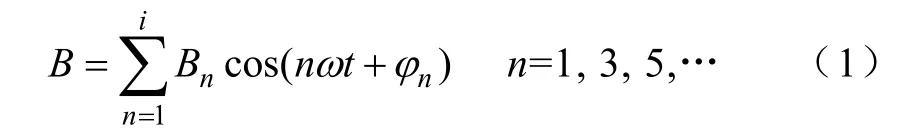
式中，Bn=1为基波磁通密度幅值，Bn=3,5,…为n次谐波磁通密度幅值（T）；φn=1为基波相位，实验中设定φ1=0°，φn=3,5,…为n次谐波相位；ω为角频率（rad/s）。

理想情况下，根据爱泼斯坦方圈的结构特征，忽略漏磁通的影响，通过电磁感应定律确定感应电压为

式中，u(t)为测量绕组的感应电压（V）；N为线圈匝数；S为铁心的横截面积（m2）。

谐波激励条件下，定义谐波含有量kn以及谐波相位差θn分别为

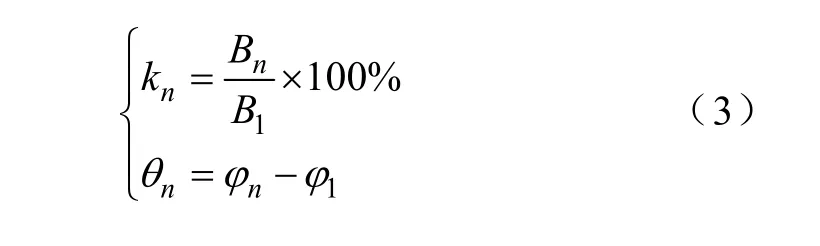
2 正弦条件下铁磁材料损耗的计算

铁磁材料损耗不仅取决于材料特性，与磁场中的激励频率以及磁通密度的大小也密切相关。因此对于取向硅钢片材料B30P105来说，在不同的激励工况下，损耗存在明显的差异。本节主要通过正弦激励作用时测量得到的铁损数据，确定损耗分离模型的表达式。

2.1 经典Bertotti损耗分离模型

意大利学者Bertotti基于磁畴理论，将铁磁材料损耗按形成机理分为磁滞损耗Ph、经典涡流损耗Pe和剩余损耗Pa三部分[21]。

根据Bertotti损耗分离理论，单位质量的铁磁材料在正弦激励（B=Bmcos(2πft)）作用的一个磁化周期内产生的铁损PBer可以表示为

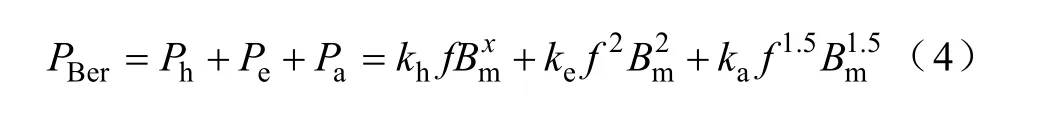
式中，kh、x为磁滞损耗系数；ke为经典涡流损耗系数；ka为剩余损耗系数；f为励磁电压频率（Hz）；Bm为磁通密度幅值（T）。

大量的实验研究结果表明，经典Bertotti损耗分离模型仅在Bm≤1.2T,f≤400Hz范围内能够准确模拟铁磁材料损耗的变化，超出此范围损耗模型的有效性大大降低[20]。

鉴于经典Bertotti损耗分离模型具有物理意义明确、计算方法简单等优势，本文旨在其基础上进行改进，推导建立一个能够准确计算较高频率以及较高磁通密度条件下铁磁材料损耗的改进损耗分离模型。

2.2 磁滞损耗

结合当前损耗计算的相关文献可以发现，磁滞损耗的计算大致采用两种方式：一是基于损耗分离理论，认为极低频率条件下测量得到的总损耗仅为磁滞损耗，然而该假设建立在忽略经典涡流损耗与剩余损耗的基础之上，并且实验激励很难控制在极低频；二是基于磁滞模型模拟磁滞回线的变化，认为磁滞回线包围的面积即为磁滞损耗值，需要指出的是，此假设仅适用于静态磁滞模型中，且计算过程较为繁杂，需要通过数值积分来实现，限制了其应用。为了避免上述两种方法的不足，在此提出一种计算磁滞损耗的新方法，即基于低频低磁通密度工况下二频率法计算得到的磁滞损耗值求解得磁滞损耗表达式。

在实验测量时，施加正弦激励信号，按照第1节所述的测量方法，测得低频低磁通密度条件下铁损的实验值，并根据二频率法求得磁滞损耗[22]，有

式中，Ph(f0)为频率为f0时对应的磁滞损耗（W/kg）；P(f1)为频率是f1时测量得到的铁磁材料损耗（W/kg）；P(f2)为频率是f2时测量得到的铁磁材料损耗（W/kg）。

频率较低的工况下，铁磁材料损耗主要为磁滞损耗与经典涡流损耗，易分离，因此采用低频5Hz、20Hz条件下测量得到的损耗数据，根据二频率法算得磁滞损耗数值。并按照式（4）第一项，实现未知参数的辨识。计算得kh=0.001 99,x=1.960 2。

2.3 经典涡流损耗

正弦激励条件下，经典涡流损耗表达式可以简化为式（4）第二项，其中，经典涡流损耗系数ke由Maxwell方程推导所得的宏观方程表示，主要由铁磁材料的性能参数决定，有

式中，σ为硅钢片电导率（S/m）；d为硅钢片厚度（m）；ρ为硅钢片密度（kg/m3）。

根据材料出厂时厂家提供的特性参数，求得取向硅钢片B30P105的经典涡流损耗系数ke值为0.000043。

2.4 剩余损耗

剩余损耗为铁磁材料总损耗中去掉磁滞损耗、经典涡流损耗后剩下的部分，与经典涡流损耗统称为动态损耗。

基于以上分析，按照式（4）第三项计算得剩余损耗系数ka与磁通密度以及与频率的变化关系曲线。图2为磁通密度恒定时，剩余损耗系数随频率的变化关系曲线，可以发现，随着频率的增加，ka先增大后减小，但磁通密度不同时，ka的变化趋势并不一致。图3为频率恒定时，磁通密度与ka的变化关系曲线，可以清晰地看出，对于不同的工作频率，ka随着磁通密度增加，整体上呈现递增趋势，但是很难找到一个具体的、简单的函数表达式，来表征ka与频率以及磁通密度之间的数量关系。因此，若想实现剩余损耗的计算，需得到一个能够同时反映剩余损耗与磁通密度幅值以及频率之间数量关系的函数。

图2 频率与ka关系曲线Fig.2 The relation curves between frequency and ka

图3 磁通密度与ka关系曲线Fig.3 The relation curves between flux density and ka

为了避开系数ka表达式求解的难题，本文基于经典Bertotti损耗分离模型，将动态损耗与经典涡流损耗的比值确定动态损耗因子，进而实现剩余损耗的求解，有

式中，D为动态损耗因子，应当是大于1的数值。通过式（7）可推导计算得到不同激励条件下，剩余损耗值=(D-1)×经典涡流损耗值。

根据学者J. Reiner等提出的MSE（modified steinmetz equation）公式可知，磁通密度随时间的变化率是关于磁通密度幅值与频率的函数，并且其对损耗的计算产生直接的影响。为此，文中采用磁通密度变化率dB/dt的有效值来确定动态损耗因子表达式，进而构建动态损耗因子与波形参数之间的函数关系。

对于正弦波形，磁通密度变化率dB/dt的有效值可以表示为

按照式（7）与式（8）计算得到的D与dB/dt的关系如图4所示（由频率为5～400Hz，Bm为0.1～1.2T工作点测量得到的取向硅钢片B30P105的铁损数据绘制而成），随着dB/dt数值的增加，D逐渐减小，这是因为，当频率增加到一定程度，经典涡流损耗数值急剧增加。通过曲线的变化趋势，清晰可见，D与dB/dt呈现出衰减的对数关系，由此采用数学拟合法，得到动态损耗系数D与磁通密度变化率dB/dt有效值之间的函数关系为

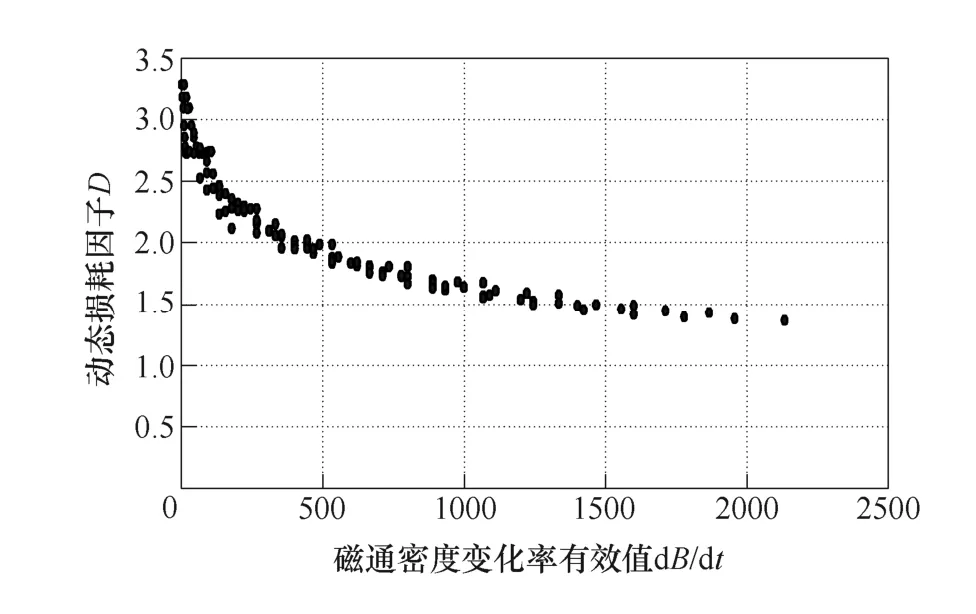
图4 磁通密度变化率有效值与动态损耗因子之间的关系Fig.4 The relationship between equivalent magnetic flux density variation and dynamic loss factor

当dB/dt的数值超过图示范围时，按照式（9）采用趋势外推法计算所需工况下的动态损耗因子D。但是当dB/dt＞5 426，根据式（9）计算得到的D＜1，进而计算得到负的剩余损耗，不符合实际的运行状态。据此文中假设当激励频率与磁通密度幅值均较高时，即dB/dt＞5 426，近似认为剩余损耗为0，动态损耗因子D=1。这是因为，在磁通密度接近饱和工作点时，剩余损耗系数减小为0，剩余损耗接近0[23]。

基于上述分析，可以建立正弦条件下的改进损耗分离模型为

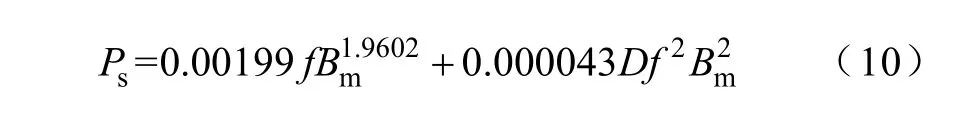
式中，Ps为正弦条件下得到的损耗值（W/kg）。

工程应用中，取向硅钢片材料一般工作在低频状态下，频率较高时，振动和温升急剧增大，为此，本节在频率小于1 000Hz之内的正弦激励条件下计算铁损，并与损耗测量结果进行对比，验证上述正弦条件下改进损耗分离模型的有效性。

图5给出了Bm=1.7T，激励频率分别为200Hz、400Hz、600Hz、800Hz、1 000Hz时，基于式（10）计算得到的损耗结果以及实验测量数据，图中数值为损耗的相对误差，有

图5 Bm=1.7T，不同频率下损耗计算值与测量值的对比Fig.5 Comparison of calculated and measured loss at different frequencies when Bm=1.7T

通过图5可以看出，在磁通密度幅值Bm=1.7T的工作点，基于损耗模型计算的数值与实际测量值的相对误差均大于10%，当频率为800Hz时，误差高达19.7%。

图6给出了f=800Hz，磁通密度为0.8T、1.2T、1.5T、1.6T、1.7T时铁损预测值与计算值对比，由图可知，随着磁通密度数值的增大（尤其是Bm＞1.2T时），基于损耗模型的预测结果较实际测量结果明显偏小，且相对误差随磁通密度的增加呈现明显的扩大趋势。这是因为，当磁通密度增加到接近饱和工作点时，硅钢片B30P105内部非线性特征格外突出，而正弦条件下建立的改进损耗分离模型未能体现出这一变化，导致损耗计算结果较小。因此需要着重研究较高磁通密度区域铁磁材料非线性对损耗的影响规律，解决当前损耗预测不准确的问题。

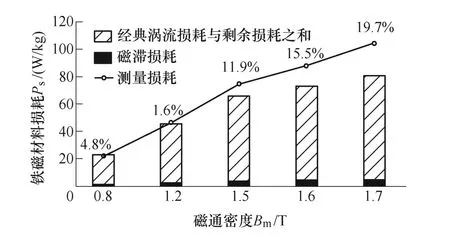
图6 f =800Hz，不同磁通密度下损耗计算值与 测量值的对比Fig.6 Comparison of calculated and measured loss at different flux densities when f =800Hz

3 建立考虑材料非线性特征的损耗模型

3.1 非线性修正项的确定

从铁磁材料的性质而言，在较强磁场作用下，材料内部呈现出很强的非线性特性。这时根据磁化线性区域确定的损耗计算模型未能对铁磁材料非线性特征做出描述，引起一定的计算误差[24]。本节在经典涡流损耗基础上引入磁通密度函数对损耗模型进行修正，以表征材料非线性对总损耗的影响，正弦条件下建立的考虑非线性修正项的改进损耗分离模型为

其中

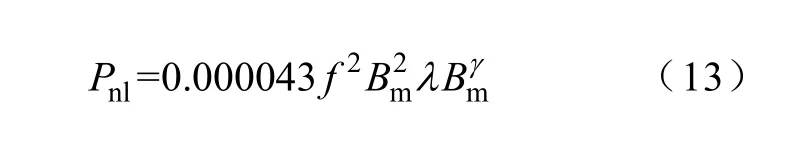
式中，Psin为铁损计算值（W/kg）；Ps由式（10）计算得到；Pnl为非线性修正项（W/kg）；λ、γ为表征材料非线性的未知参数，与材料特性有关。

简要分析式（10）在频率为5～1 000Hz正弦激励作用下的损耗计算结果，发现在各个磁化频率点，磁通密度较高时损耗的计算结果均明显低于测量结果，因此，根据Bm为1.2～1.7T的工作点测量得到的铁损数值求解式（13）中的未知参数。计算得，λ=0.004 8；γ=7.287 3。

3.2 损耗模型的验证

根据3.1节确定的正弦条件下考虑非线性修正项的改进损耗分离模型预测铁损，计算结果见表2。可以看出，在多种正弦激励信号的作用下，损耗相对误差基本保持在5%之内。

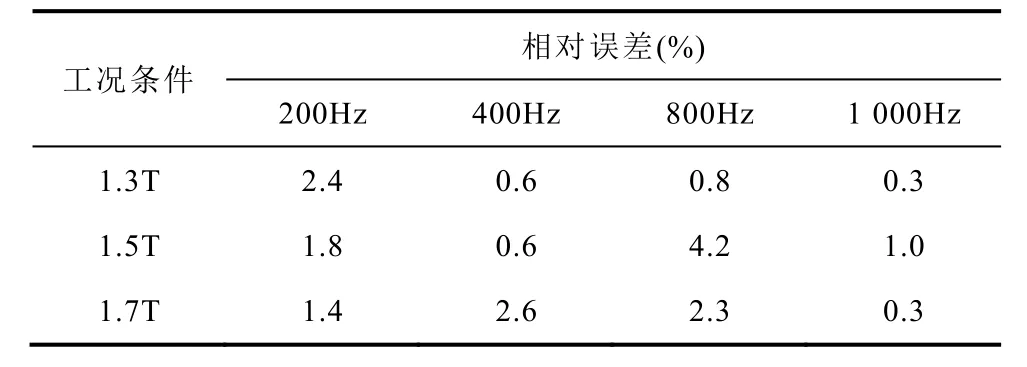
表2 正弦条件下损耗计算值与测量值的相对误差Tab.2 Error of calculated and measured loss under sinusoidal condition

对比分析图5、图6与表2的计算结果可以发现，引入非线性修正项后，损耗计算误差明显减小，由此可以认为，正弦条件下考虑非线性修正项的改进损耗分离模型能够明显提升较高磁通密度区域损耗的计算精度，具有更宽的磁通密度适用范围。

4 谐波条件下考虑非线性修正项的改进损耗分离模型的建立与验证

4.1 谐波条件下改进损耗分离模型的建立

在实际的运行过程中，铁磁材料的激励信号很少会是理想的正弦波，其中，谐波激励是极为常见的工作条件。为了实现谐波激励条件下铁损的准确计算，本文做出如下假设：当磁通密度较低（Bm≤1.2T）时，材料特性近似为线性变化，可采用叠加的方法实现损耗计算；在此基础上，当磁通密度较高（1.2T≤Bm≤1.7T）时，基于3.1节提出的非线性修正项来表征材料的非线性特征，建立改进损耗分离模型为

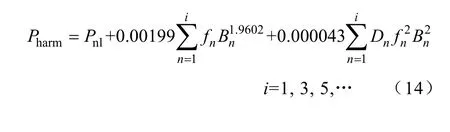
式中，Pharm为谐波激励条件下损耗预测值（W/kg）；fn=1为基波励磁频率，fn=3,5,…为n次谐波的励磁频率（Hz）；Dn=1为基波动态损耗因子，Dn=3,5,…为n次谐波的动态损耗因子。

4.2 谐波条件下改进损耗分离模型的验证

实验时根据变压器实际运行时可能遇到的激励条件设计了几种典型的谐波激励信号，部分激励信号如下所述：谐波激励信号1：基波叠加含量k7=30%的7次谐波，θ7=45°；谐波激励信号2：基波叠加含量k7=30%的7次谐波，θ7=0°；谐波激励信号3：基波叠加含量k5=20%的5次谐波，θ5=90°。需要指出的是，文中选取的谐波激励信号1、2、3是具有代表性的工况，体现出了基波与不同含量、不同相位、不同阶次的谐波的叠加。

基于以上谐波激励信号1、2、3，按照第1节搭建的磁性能测试系统测得损耗实验结果，并基于本文所提出的谐波条件下考虑非线性修正项的改进损耗分离模型计算铁损，将二者进行对比分析，进一步验证该损耗模型的准确性。

图7所示为谐波激励信号1工况下各部分损耗计算值与实验测量值对比，可以较为直观地看出各部分损耗之间的关系。图7中，在各个磁通密度工作点，左侧为磁滞损耗、动态损耗以及非线性修正项三部分表征的总损耗计算值，右侧为损耗测量值，可以发现，损耗计算值与测量值基本一致，例如，当Bm=1.7T时，损耗实测值为2.333 6W/kg，磁滞损耗值为0.282 1W/kg，经典涡流损耗与剩余损耗之和为1.895 1W/kg，非线性修正项为0.071 3W/kg，总损耗为2.248 5W/kg。

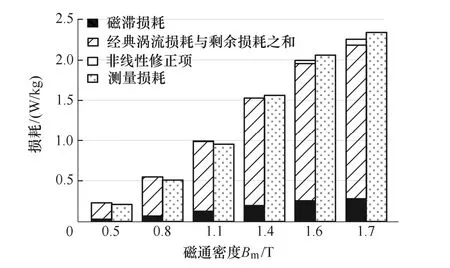
图7 谐波激励信号1工况下损耗计算值与 测量值的对比Fig.7 Comparison of calculated and measured loss under harmonic excitation signal 1

从图7还可以看出，随着磁通密度的增加，三种损耗均呈现出增加的趋势，并且在较高磁通密度区域经典涡流损耗所占的比重最大。相比之下，在低磁通密度区域非线性修正项数值最小，几乎可以忽略不计，但随着磁通密度的增加，逐渐明显，不可忽略。

类似地，激励信号2与激励信号3工况下损耗误差分析见表3和表4。分别列出了考虑非线性修正项与未考虑非线性修正项时铁损的计算结果以及相对误差。

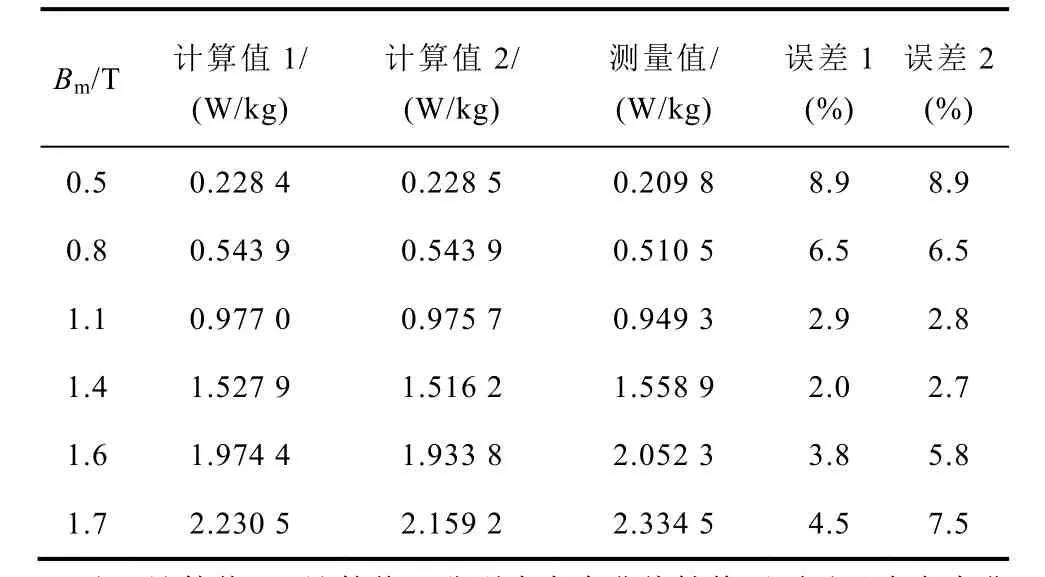
表3 谐波激励信号2工况下损耗计算值与 测量值的对比Tab.3 Comparison of calculated and measured loss under harmonic excitation signal 2

表4 谐波激励信号3工况下损耗计算值与 测量值的对比Tab.4 Comparison of calculated and measured loss under harmonic excitation signal 3

对比分析表3、表4中的误差1与误差2数据可以发现，虽然当磁通密度较低时，非线性修正项的引入对损耗计算结果的影响几乎可以忽略不计，但随着磁通密度的增加，当磁通密度达到1.4T及以上时，相比于未考虑非线性修正项时的损耗计算结果，引入非线性修正项明显降低了损耗的计算误差，例如，表3中，当磁通密度为1.7T时，损耗计算误差由7.5%降低为4.5%，表4中，损耗计算误差由10.7%降低为5.5%，并且在磁通密度较高的情况下，本文所建立的考虑非线性修正项的改进损耗分离模型均能较为准确地实现铁磁材料损耗的计算，验证了该模型的有效性以及可行性。

通过图7、表3、表4所示结果，可以认为该考虑非线性修正项的改进分离损耗模型可以考虑谐波含量、相位、阶次不同时的损耗变化，并且当存在局部磁滞回环时，亦能准确反映铁磁材料的损耗特征。

综上所述，本文建立的谐波激励条件下的改进损耗分离模型可以较为精确、快速地实现铁磁材料损耗的计算，能够作为一种解决损耗计算问题的工程应用新方法。

5 结论

文中按照国家标准搭建了磁通密度可控的实验测试平台，利用正弦条件下测量的损耗数据，建立了适用于谐波激励条件下铁磁材料损耗计算的改进损耗分离模型。重点工作总结如下：

1）根据实验测量数据，引入动态损耗因子计算剩余损耗，避免因剩余损耗系数求解不精确而导致计算误差加大。考虑到磁通密度较高时损耗计算结果明显小于测量结果这一问题，提出采用非线性修正项来弥补损耗计算误差，进而建立了改进的损耗分离模型。实验结果表明，无论是正弦较高频率还是谐波激励条件下铁损的计算，必须充分考虑材料非线性的影响。

2）本文建立的考虑非线性修正项的改进损耗分离模型具有物理意义明确、计算方法简单、计算结果准确等优点，为工程上铁磁材料损耗的计算提出新的思路。