紫外光通信散射信道模型分析与发展现状

袁仁智，王志峰，彭木根

（1.加拿大英属哥伦比亚大学奥肯纳根校区工程系，基隆拿 V1V1V7，加拿大； 2.北京邮电大学信息与通信工程学院，北京 100876）

1 引言

无线光通信技术具有容量大、速率高、抗干扰性强、组网机动灵活等优点，是未来6G通信[1-3]的重要实现方式之一。其中，与其他波段的光通信技术相比，近地面利用“日盲区”波段（200～280 nm）作为信息载体的紫外光通信技术具有极低的背景噪声，这是因为大气层尤其是臭氧层对太阳背景辐射中“日盲区”波段紫外光的强烈吸收和散射[4-5]。同时，近年来，紫外LED技术和紫外探测技术的飞速发展也使得开发小型化和商业化的紫外光通信系统成为可能，进而使紫外光通信逐渐成为光通信领域的研究热点之一。除了具有极低背景噪声的优势，大气颗粒和气溶胶对紫外光波的强烈吸收和散射也使紫外光通信具备局域保密通信和非视距通信的能力[6]。此外，在大雾或者强降雨等低能见度的恶劣天气状况下，其他波段的光通信系统性能将受到很大的影响，而建立在大气颗粒和气溶胶散射基础之上的紫外光通信系统在恶劣天气状况下仍能有效工作[7]。因此，紫外光通信在保密通信领域（如作战单位之间的通信、航母编队的内部通信等）和民用通信领域（如车联网安全通信、无人机在恶劣天气下的救援救灾等），都具有广泛的应用前景。

1.1 国内外紫外光通信研究现状

美国最早开展紫外光通信研究[8-9]，主要的科研单位有麻省理工学院、加州大学河滨分校、美国国防部高级研究计划局（Defense Advanced Research Projects Agency，DARPA）等，在紫外LED通信的理论和实验领域做了大量工作，目前已经可以实现短距离100 m内非视距紫外LED通信[10]。加拿大从事紫外光通信的研究机构主要有英属哥伦比亚大学和麦克马斯特大学。英属哥伦比亚大学在紫外信道建模和实验方面都展开了研究[11-12]，实现了100 m以上大仰角的非视距紫外LED通信。麦克马斯特大学以理论研究为主，在2011年首次将单次散射模型推广至任意收发几何情形[13]。沙特阿卜杜拉国王科技大学曾搭建通信速率为71 Mbit/s的LED紫外光通信验证实验，不过通信距离只有几厘米[14]。

国内在紫外LED通信领域的主要研究机构有北京邮电大学、清华大学、中国科学技术大学等研究单位。例如，北京邮电大学在紫外光通信信道建模领域做了大量研究[15]；清华大学在紫外光通信信道建模以及实验方面都进行了研究[16-17]，搭建100 m内紫外LED通信系统，实现了大仰角非视距紫外LED通信；中国科学技术大学近年来进行了大量短距离紫外LED通信验证实验[18]。

当前对紫外光通信的研究总体上仍处于点对点和短距离通信验证的阶段。未来为了实现紫外光通信的实用化和商业化，需要重点研究紫外组网通信和紫外长距离通信。紫外光通信是基于紫外光散射特性的通信方式，具有独特的信道模型，因而紫外组网通信和紫外长距离通信的研究具有与其他波段光通信不同的特点。因此在研究紫外组网通信和紫外长距离通信前，有必要先深入研究紫外光通信的信道模型。

1.2 紫外光通信的信道模型研究

典型的紫外光通信过程如图1所示。具有一定发射角度的紫外光从发射端发出，光子被大气中的颗粒分子和气溶胶等散射或者吸收一次或者多次，部分散射光子到达接收端探测器被接收。利用散射光进行通信，可以实现绕过障碍物的非视距通信。对紫外光通信散射信道模型的准确建模有助于提高对系统信道状态信息的估计精度，对后续接收信号的解调、多用户发射功率分配、系统收发端几何调整以及紫外光定位功能的实现等都具有重要意义。

图1 典型的紫外光通信过程

与其他波段光通信的信道建模不同，紫外光通信的信道模型需要考虑紫外光在大气中强散射特性导致的多阶散射影响，这给紫外光通信信道模型的研究带来了挑战。早期的信道模型研究集 中在单阶散射模型[8-9,15-16,19-20]，随着通信距离和通信性能要求的提高，近年来多阶散射信道模型的研究逐渐成为研究重点[11-12,21-23]。不同于以往将信道模型分为单阶散射模型和多阶散射模型[4-5]，本文将紫外光通信散射信道模型分为解析类信道模型和概率类信道模型。此分类依据是解析类信道模型的计算效率远远高于概率类信道模型的计算效率。本文分别介绍解析类信道模型中的单阶、两阶、三阶散射模型以及概率类信道模型中的蒙特卡洛仿真（Monte-Carlo simulation，MCS）模型[21]和蒙特卡洛积分（Monte-Carlo integration，MCI）模型[11-12,22]，并展望了这两类散射信道模型的未来发展方向。

2 解析类信道模型

解析类信道模型是将散射模型表示为一个能够用现有计算软件快速计算的多重（一般不超过三重）积分形式。目前的解析类信道模型主要有单阶散射模型[8-9,15-16,19-20]、两阶散射模型[17]和三阶散射模型[17]。这类模型的优点就是计算速度快，通常在秒级，缺点是应用场景受限，几乎无法推广到复杂应用场景。比如单阶散射积分模型通常只能估计100 m以内的信道损耗；现有的两阶和三阶解析模型只能计算小发射角情形下的信道损耗[17]。对于高于三阶的散射，100 m以上远距离、大发射角度或者更复杂场景（存在障碍物，反射边界等）情形，目前暂无合适的解析类信道模型。

2.1 单阶散射模型

单阶散射模型假设光子只经过一次散射即被接收端接收。图2为单阶散射模型的几何参数定义。ϕ1和θ1分别为发射端（Tx）的发射光束（Beam）的发散角和仰角，ϕ2和θ2分别为接收端（Rx）的接收视场（field of view，FOV）的发散角和仰角，r为收发端的直线距离，V表示FOV与Beam的公共区域。

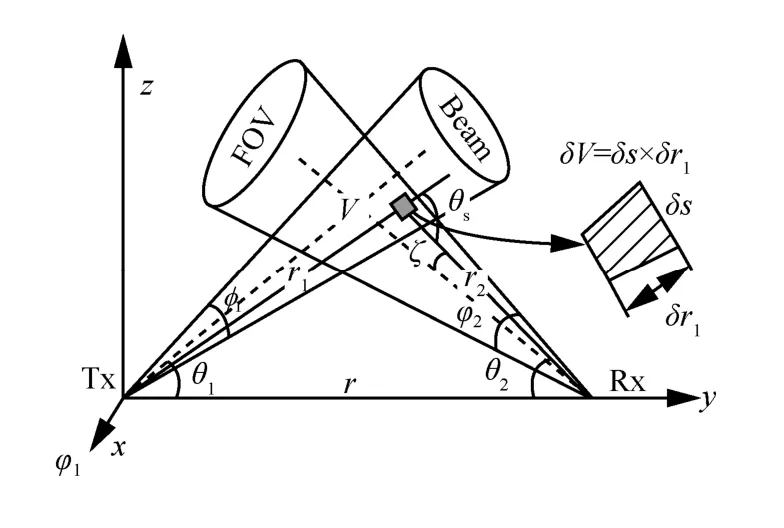
图2 单阶散射模型的几何参数定义

设δV为公共区域V中的任意一个微元体，r1为Tx到σV的距离，r2为δV到Rx的距离，θs为r1与r2的夹角，ζ为r2与FOV中轴线的夹角。则经由公共区域V内的所有微元体散射后被Rx接收的光功率可以表示为[8-9]：

其中，Pt为发射端发出的紫外光功率，Ar为接收端的接收面积，为发射端立体角，ks为大气散射系数，ka为吸收系数，为消散系数。为由瑞利散射和米氏散射共同确定的相散函数[12-13]。借助不同的坐标系，可以将式（1）写成不同的三重积分形式。

2.2 两阶散射模型

两阶散射假设光子经过两次散射到达接收端。图3为两阶散射模型的几何参数定义[17]，θT和βT分别为Tx端的天顶角和发散角，θR和βR分别为Rx端的天顶角和接收视场FOV角。

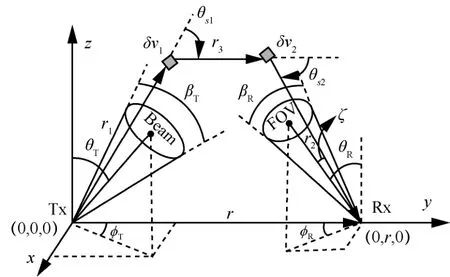
图3 两阶散射模型的几何参数定义[17]

设δv1和δv2分别为两次散射点的微元体，r1为Tx到δv1的距离，r2为δv2到Rx的距离，r3为到δv2的距离。θs1为r1与r3的夹角，θs2为r3与r2的夹角。则两阶散射接收端的接收功率可以表示为[17]：

其中，V1和V2分别为整个Beam区域和整个FOV视场区。需要指出的是，因为式（2）包含两个体积分，在具体的坐标系中则为六重积分，因此目前的数值积分工具难以精确计算式（2）。与单阶散射模型类似，可以考虑某些特殊收发几何情形下的近似计算方法。

例如，当假设发射端Beam角和接收端FOV角比较小时，可用两个球冠薄层取代δv1和δv2，则此时可将式（2）简化为[17]：

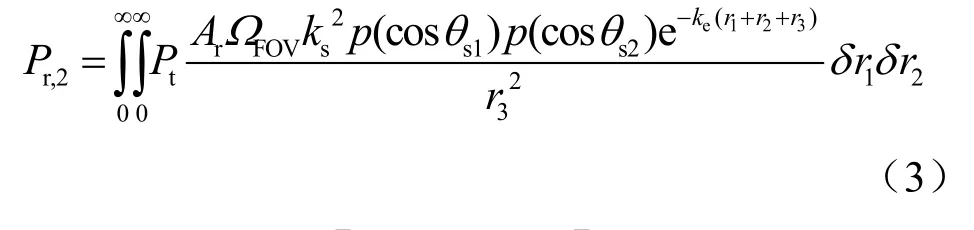
2.3 三阶散射模型

三阶散射假设光子经过3次散射到达接收端。图4为三阶散射模型的几何参数定义[17]，光子从Tx端出射后，依次被δv1、δv3和δv2散射，最后被Rx接收。三阶散射信道的接收功率可以表示为[17]：

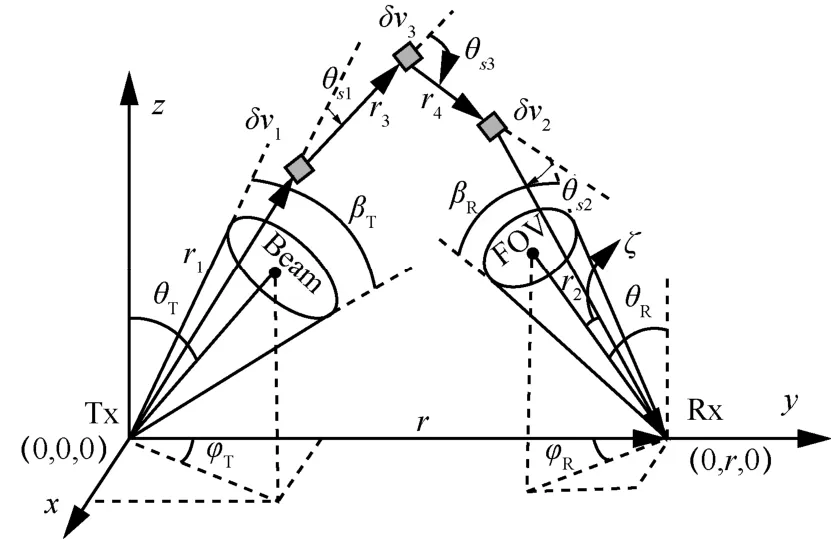
图4 三阶散射模型的几何参数定义[17]

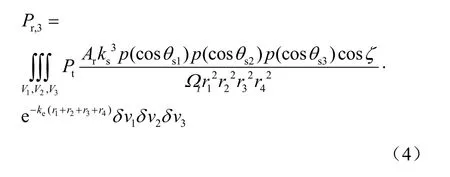
其中，积分区域V1和V2分别为整个出光光束区域和整个接收视场区域，V3为全空间。

与两阶散射模型类似，可以考虑发射端Beam角和接收端FOV比较小时的近似计算方法。参考文献[17]采用移动的椭球坐标系推导了各向同性相散函数情形，即时的三阶散射在小发散角度的近似公式[17]：

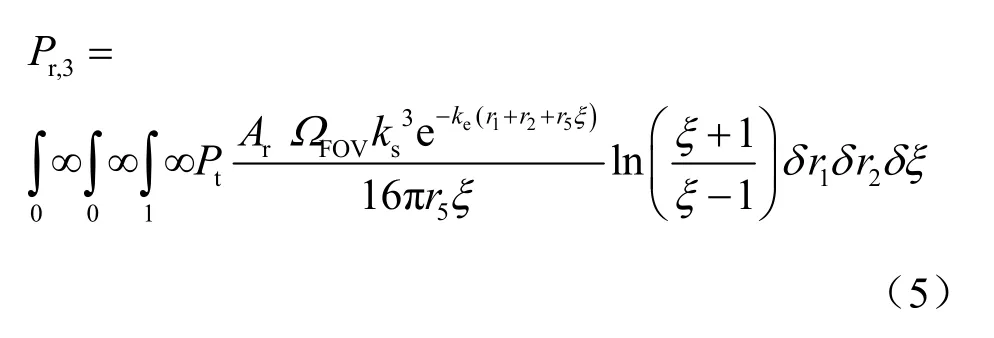
其中，r5表示散射点δv1到散射点δv2的距离。

2.4 解析类信道模型的发展和展望

解析类信道模型是最早出现的紫外光通信信道模型，其中单阶散射模型是最早出现、最多被研究的解析类信道模型。首个单阶散射模型由Reilly基于椭球坐标系建立[8]，并在1991年由Luettgen完善[9]。2011年，Elshimy等人[13]基于椭球坐标系推导了任意收发几何情形下精确的单次散射模型。椭球坐标系可以方便地求取系统单位脉冲效应，因为散射点在同一椭球面上的任意两条光子传输路径长度相同，从而具有相同的接收时间。2012年，Zuo等人[15]基于球面坐标系推导了任意收发几何情形下精确的单次散射模型。球面坐标系的三角法不需要进行复杂的坐标变换，但是球面坐标系不便于计算系统的单位脉冲响应。除了精确的单阶散射模型，为了简化计算难度，各种近似的单阶散射模型被相继提出[16,19-20]。比如：2010年，Yin等人[19]推导了当积分区域V具有各向同性时接收功率的计算式；2011年，Wang等人[20]推导了收发端公共散射体V很小时接收功率的近似计算式； 2019年，Wu等人[16]利用球冠近似方法推导了窄Beam角时单散射接收功率的计算式。参考文献[17]最早研究两阶散射和三阶散射的解析类模型，并提出了小发散角情形下的近似模型。参考文献[23]根据空间光子出现的概率大小提出了一种利用典型点代替其周围微元体的方式，简化了两阶散射接收功率的计算方法。其计算逻辑是先将积分体划分为很多个单元格，然后用单元格中心点的散射功率取代单元格的散射功率，最后将所有单元格的散射功率相加即可。但这种方法目前只能用于计算单阶散射和两阶散射情形。

尽管目前单阶散射模型的研究已趋于完善，但由于其假设光子只经一次散射，因此单阶散射模型只能用于分析短距离（通常小于100 m）的情形，对于更长距离的紫外光通信，需要考虑多阶散射的影响。此外，在紫外光通信的准备阶段或者紫外光定位场景中，往往初始时的发射端Beam角与接收端FOV并没有公共区域，此时单阶散射的接收功率为0，而两阶及两阶以上散射成为主要的接收功率来源。紫外光定位等应用场景要求在发射端Beam角与接收端FOV没有公共区域时也能快速估计信道损耗，而概率类信道模型往往计算效率低下，这促使研究人员重新重视紫外光通信中多阶散射的解析类信道模型，尤其是两阶散射的解析类模型。例如参考文献[17]提出的小发散角模型有望推广至四阶及以上阶次的散射信道；参考文献[23]提出的单元格方法有望推广至三阶及以上阶次的散射信道，且关于单元格的形状、大小、范围等要素仍有继续深入研究的必要。可以预见，未来对多阶散射的解析类信道模型的研究将成为新的研究热点。

3 概率类信道模型

概率类信道模型是利用概率论方法模拟光子的发射、传输、散射、接收过程并利用蒙特卡洛方法计算光子的最终平均接收概率。目前的概率类信道模型主要分为MCS模型[21]和MCI模型[11-12,22]。这类模型的优点是可以对远距离、任意收发几何以及复杂场景进行建模。但概率模型的缺点是计算效率低，因为蒙特卡洛方法需要对大量光子（通常在106量级以上）的仿真结果进行平均。因此，如何提高概率类信道模型的计算效率一直是概率类信道模型的研究重点和难点。

3.1 蒙特卡洛仿真（MCS）模型

蒙特卡洛仿真模型是从数理统计的角度出发，为光子的发射、传输、散射和接收等各个过程建立相应的概率模型或随机过程，然后利用大量光子重复整个随机过程，统计出每个光子接收概率并计算相应的接收时间，前者可用于求取紫外光通信的路径损耗，后者可用于求取系统的脉冲响应。

图5是MCS模型的几何参数定义[21]。为了方便接收概率的计算，将接收端置于坐标原点，发射端位于坐标(0,r, 0)处。设 (θ0,φ0)表示光子从发射端发出时的天顶角和方位角。假设光源为均匀分布，则光子的初始发射方向由式（6）、式（7）产生[21]：

图5 MCS模型的几何参数定义[21]

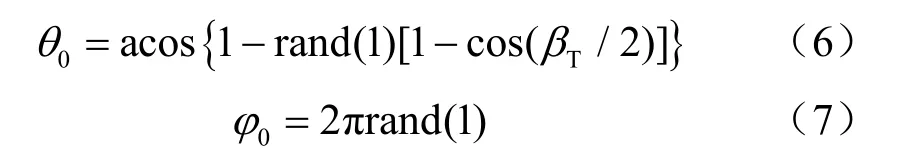
其中，rand(1)为随机产生一个[0,1]内的数。光子每次离开发射端或者散射体后的行进距离服从指数分布，则光子离开第i个散射体（其中i= 0对应光子离开发射端）后的传输距离由式（8）产生[21]：

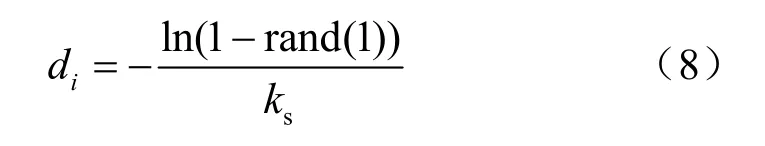
光子被散射体散射后的方向发生了改变，设(θi,ϕi)表示第i次散射后光子偏离原来行进方向的 角 度(θi,ϕi) 满 足 概 率 密 度 函 数f(θi,ϕi)=P(θi,ϕi) sinα，其中P(θi,ϕi)为相散函数[21]。则(θi,ϕi)可由式（9）、式（10）产生[21]：

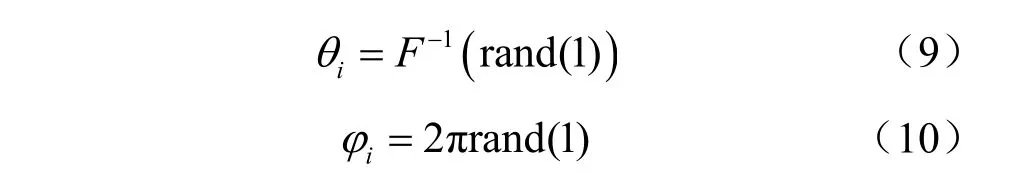
其中，F(θi)为f(θi,ϕi)关于θi,的边缘概率分布函数。

光子在每次散射后，若位于接收视场FOV内，则计算光子被探测器接收的接收概率。假设第i个散射点与接收面形成的立体角为Ωi，散射点的坐标向量为ri，光子原行进方向与ri的夹角为θri，则光子此时的i阶散射接收概率为[21]：

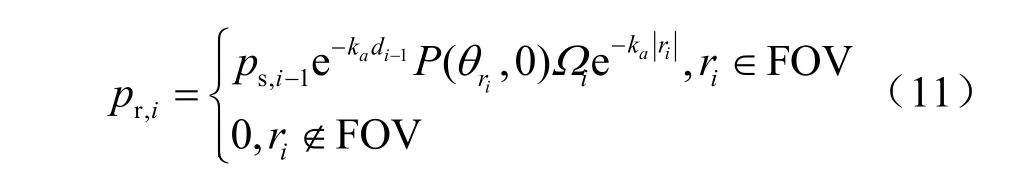
其中，ps,i-1为第i次散射前的存活概率。每次接收判断之后更新光子存活概率为[21]：

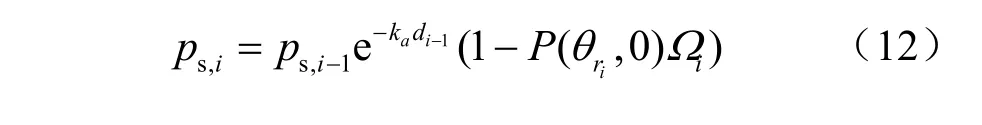
单个光子的蒙特卡洛过程如图6所示。预先为每个光子设定一个散射阶次上限以及最小存活概率，作为判决光子是否消失的条件。首先，初始化散射阶次i= 0和光子序号k=1；然后，根据不同的采样函数依次对光子距离d、散射角θ和方位角ϕ进行采样；然后更新光子的位置和光子存活概率，并对光子位置进行判断，如果光子位于接收视场内，则计算光子的接收概率和接收时间。用大量光子重复上述过程，记录所有光子各个阶次的接收概率，则光子的接收概率可以用所有光子的平均接收概率来估计。由于过程中能够方便得到每个接收概率对应的总行进距离，除以光速即可得光子的接收时间，将所有接收概率按接收时间统计，即得到系统的脉冲响应函数。

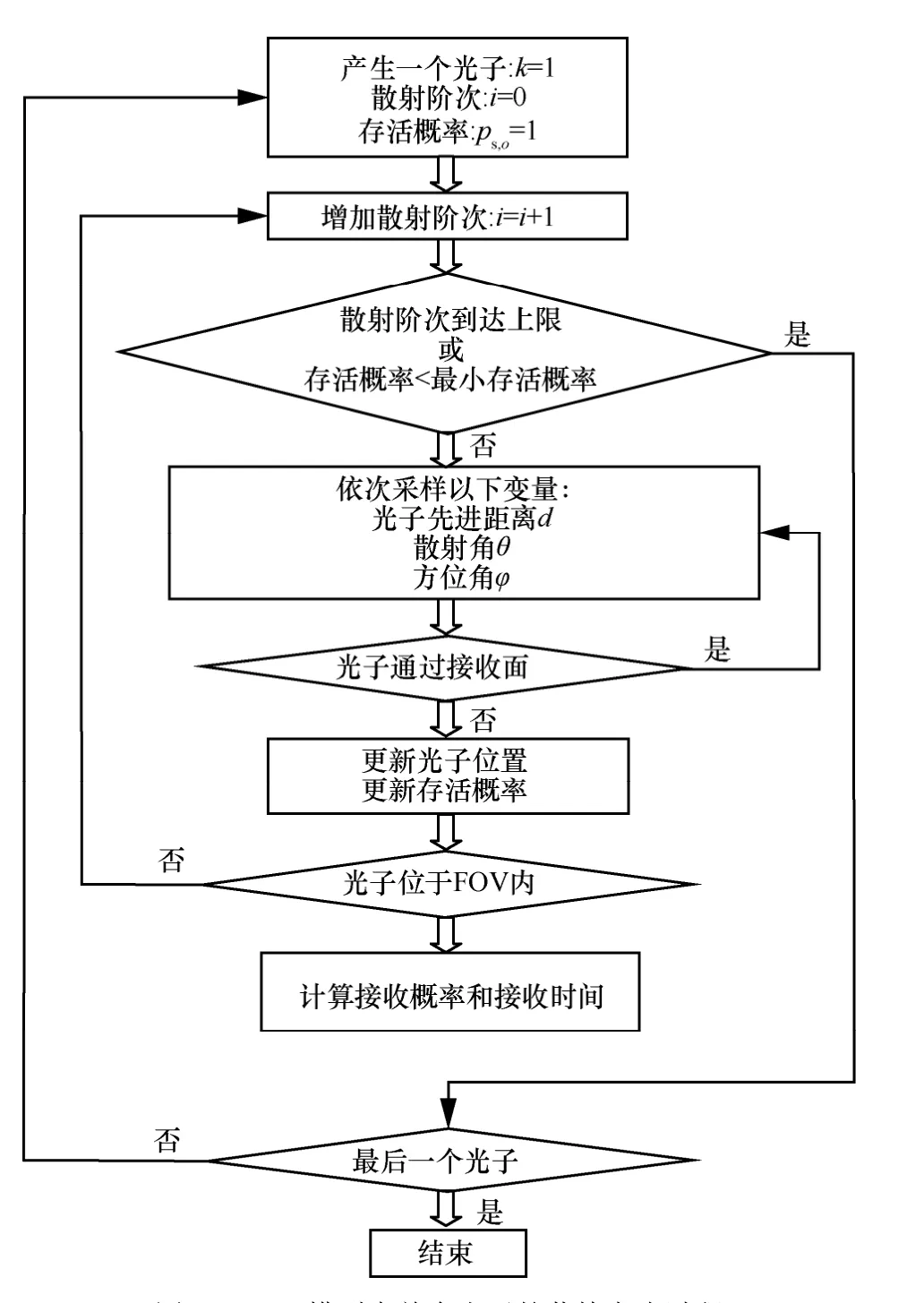
图6 MCS模型中单个光子的蒙特卡洛过程

3.2 蒙特卡洛积分（MCI）模型

MCI模型是一种概率积分方法，它首先将接收功率表示为一个关于光子传输参数的概率积分，然后采用蒙特卡罗积分技术求取此概率积分[22]。MCI模型已被证明同样可以用于计算系统脉冲响应函数[12]，与MCS模型相比，MCI模型的计算逻辑更清楚，计算结构更简单，且MCI模型的计算效率可以通过采取不同的采样函数进行优化，因此MCI模型在近年成为概率类信道模型的研究热点。

3.2.1 多阶散射信道的概率积分

图7显示多阶散射过程的参数定义，μT和μR分别为发射端Beam和接收端FOV中心轴线的方向向量。假设光子初始出射过程为零阶散射过程，di、θi和ϕi分别表示第i阶散射的光子传输距离、散射天顶角和散射方位角；第i个散射点的坐标向量为ri，第i阶散射后光子行进的方向向量为μi。

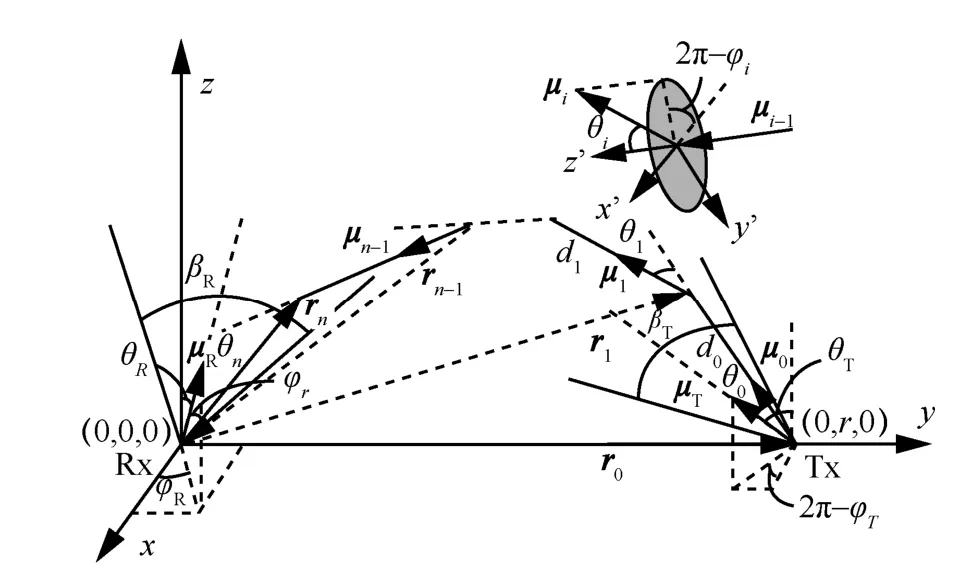
图7 多阶散射参数定义

对于第i阶散射，散射后光子传输方向位于微元立体角dΩi= sinθidθidϕi内且传输距离位于(di,di+ ddi)内的概率为[12]：

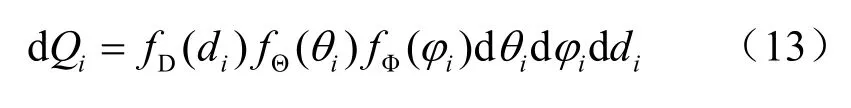
其中 ，fD(di)=为传输距离di的概率密度函数（probability density function，PDF），为散射方位角ϕi的PDF，fΘ(θi)为散射天顶角的PDF，且。对于i＞ 0，fΘ(θi)由瑞利散射和米散射的相散函数加权得到：

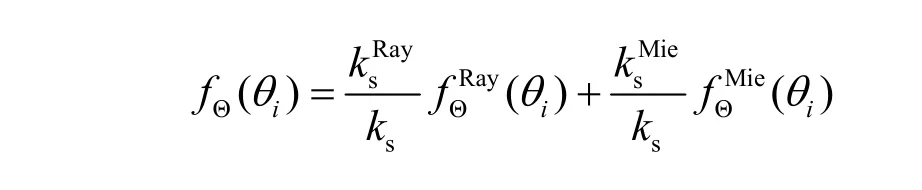
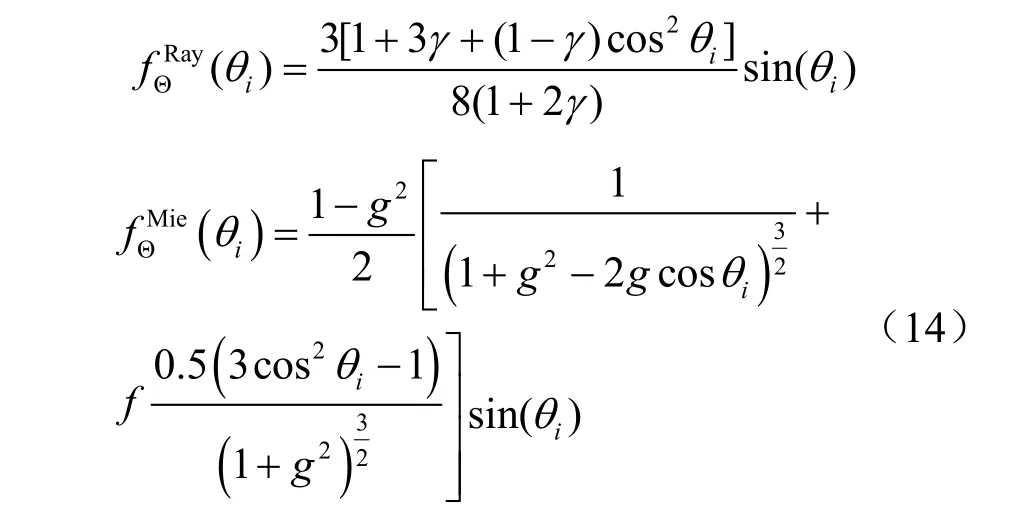
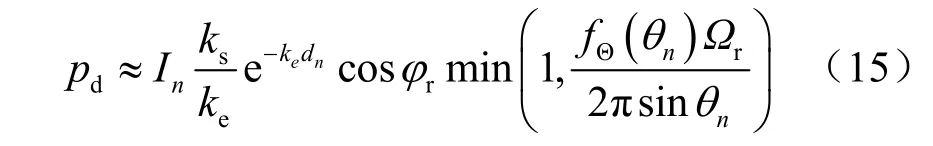
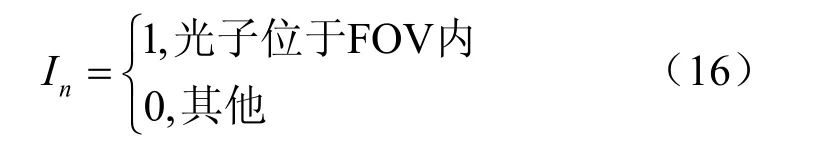
于是光子从发射端出射，经过n阶散射后被接收端接收的概率为[12]：

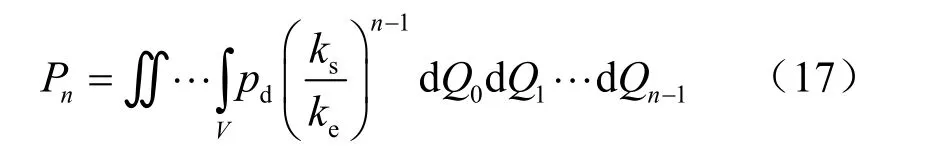
其中，V为维的积分区域。

3.2.2 蒙特卡洛积分方法的引入

式（18）是一个没有闭式解的超越积分，只能采用数值积分的方法计算，这里引入蒙特卡洛积分方法。先将式（17）写成[12]：

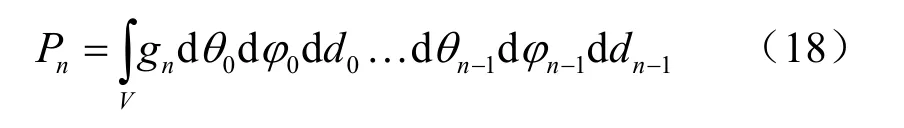
其中：

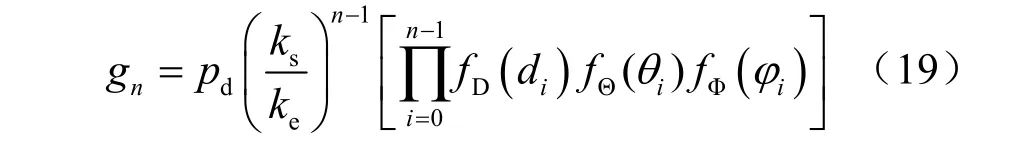
然后再在积分空间V上选择一个概率密度函数fn≠ 0，并引入一个目标函数：

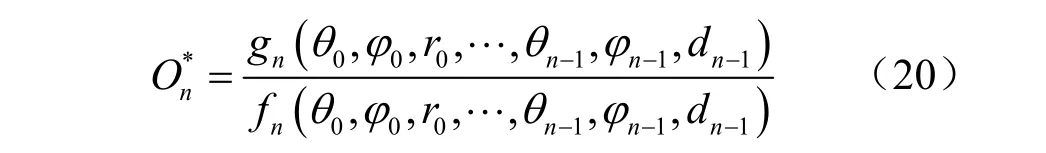
则式（18）可以改写成：

式（21）表示，n阶散射信道的接收功率Pn等于用采样函数fn进行采样时目标函数的数学期望。如果在积分空间内随机采样N个采样点(x1,x2,…,xN)，其中：

则对每个xi都可以计算一个相应的目标函数值。根据大数定律，所有目标函数值的平均值可以作为目标函数数学期望的估计，即：

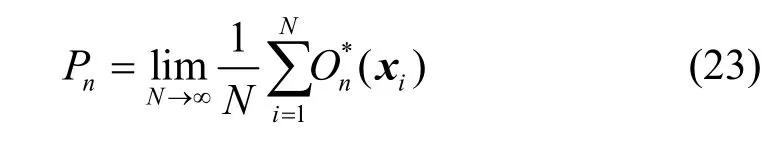
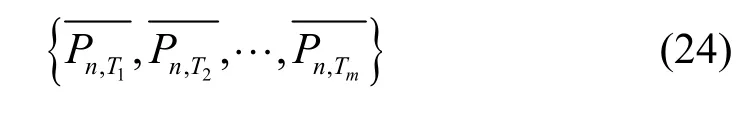
将此序列按照时间间隔接收面积归一化，即得到系统的脉冲响应函数。

3.2.3 基于部分重要性采样的MCI模型（MCI-PIS）

尽管在MCI方法中，采样函数fn的选择可以是任意的一个定义在积分空间上的概率密度函数，但是不同的fn将影响模型的收敛速度，这里介绍一种基于部分重要性采样的MC（IMCI based on partial importance sampling，MCI-PIS）模型。注意n阶散射信道的接收概率的大小主要取决于光子总路径的长短，因此影响MCI模型收敛性的主要因素为对光子行进距离d的采样方式。因此考虑如下部分重要性采样函数fn，其中只对光子行进距离采用重要性采样方法，而对散射天顶角和散射方位角采用均匀采样方法[12]：

MCI-PIS模型综合考虑了采样速度和收敛速度的优化，是目前已知的计算效率最高的MCI模型。图8显示了MCI过程的计算流程，在运行MCI过程前，先设定光子的最高散射阶次和最大采样光子数作为停机条件。首先，初始化散射阶次i= 0和光子序号k=1；然后，根据设定的采样函数依次对光子传输距离d、散射天顶角θ和散射方位角ϕ进行采样；最后，更新光子的位置，并对光子位置进行判断，如果光子位于接收视场内，则计算光子的接收概率接收时间。对比图6中的MCS过程，可以看到MCS过程额外引入了一个中间变量光子存活概率ps，并且对光子的传播路径增加了几何条件限制（光子在两个散射点之间传播时不能穿过接收区域）[12]。额外的存活概率计算和光子路径判断使得MCS过程相比于MCI过程更加复杂。需要指出的是，由于MCS模型是仿真光子在物理空间中的传播和散射过程，MCS模型中的几何限制是有意义的；但是MCI模型中的对每个随机变量的采样是在数学空间中进行的，因此可以将这些几何限制去掉而几乎不影响MCI的计算精度[12]。

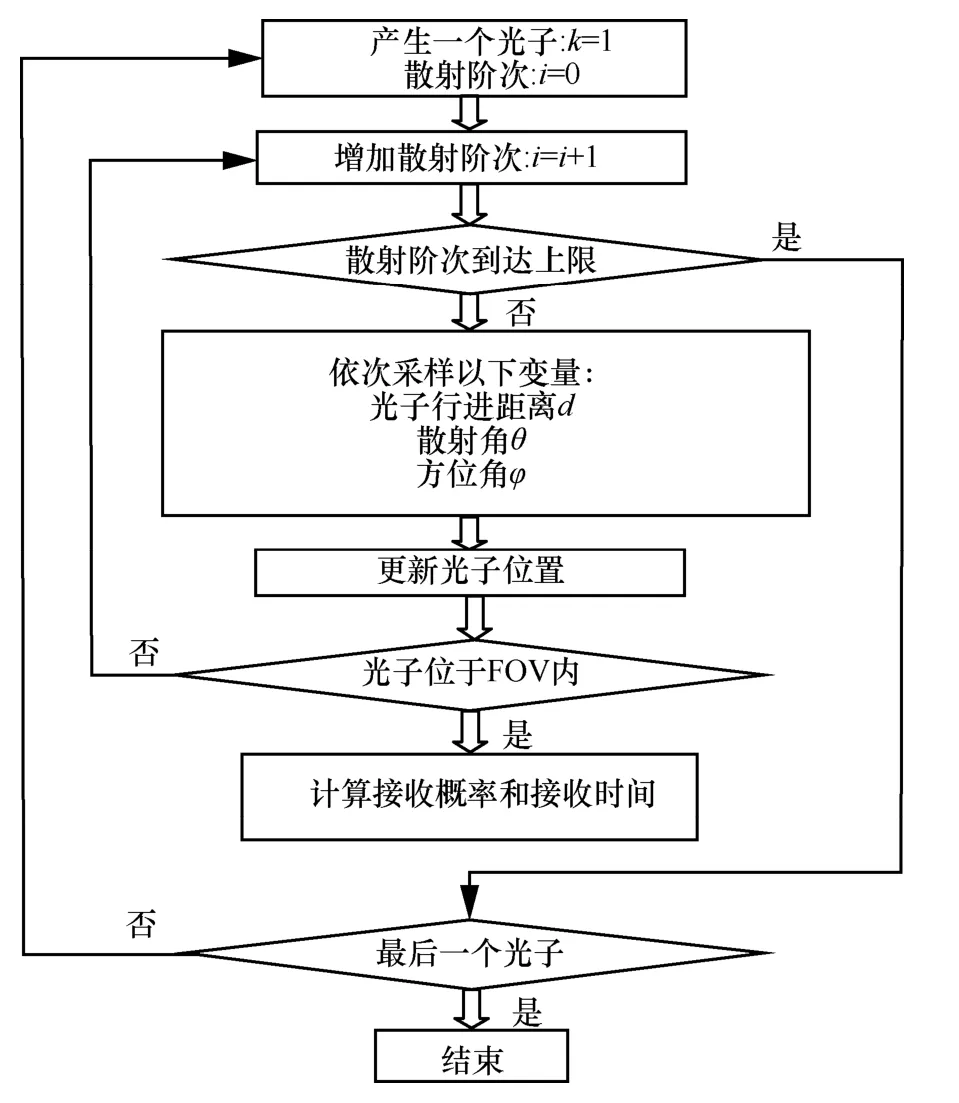
图8 MCI模型中单个光子的蒙特卡洛过程

3.3 概率类信道模型的发展和展望

最早应用于紫外光通信的概率类信道模型是MCS模型，早期的MCS模型通过统计到达接收端的光子数来估计光子探测概率，这种计数方法需要的仿真光子数十分巨大，模型效率低下。2011年，Drost 等人[21]通过计算每个光子的到达概率以及优化光子传输距离的采用方式大大降低了仿真所需的光子数。但对于长远距离的仿真使用MCS模型仍然困难，如何提高概率类信道模型的计算效率一直是紫外光通信多阶散射信道建模的重要课题。2010年，Ding等人[22]提出了首个MCI模型，但是首个MCI模型中所有变量都采用均匀采样，大大降低了MCI模型的采样效率，且模型未能解决脉冲响应函数的计算问题。2020年，Yuan等人[11-12]系统地改进了MCI方法，提出了基于重要性采样的MCI-IS模型[11]和基于部分重要性采样方法的MCI-PIS模型[12]，其中后者的计算效率比原始MCI模型高出一个数量级，是MCS模型计算效率的5.6倍，大大提高了概率类信道模型的计算效率[12]。

现有的概率类信道模型仍有诸多改进空间，例如在光源分布和接收模型的处理上需要更加贴近实际情形。同时，对于有障碍物环境下的建模以及对障碍物表面的反射或吸收性质的处理也需要进一步研究。而且，概率类信道模型多用于远距离紫外光通信的信道估计，因此信道建模还需考虑大气湍流的影响，这方面虽有一些初步的探索[24-25]，但是离实用的湍流信道模型仍有很大的改进空间。最后，将概率类信道模型与解析类信道模型相结合的信道建模方法有望兼备两者的优点，在提升计算效率的同时，满足复杂场景的建模需要，这也会是未来紫外光通信信道建模的研究方向之一。

4 结束语

紫外光通信由于其局域保密性、低背景噪声、非视距通信等特点，在保密通信和民用车联网安全通信领域都有广泛应用场景，近年来已成为光通信中的研究热点之一。对紫外光通信性能的分析离不开信道模型对信道状态信息的估计。大气对紫外光的强散射特性，使得对紫外光通信信道建模的研究需要考虑多阶散射的影响，这给紫外光通信信道建模增加了难度。本文回顾和总结了紫外光通信散射信道模型的发展和现状，将散射信道模型按照计算效率分为解析类信道模型和概率类信道模型，分别介绍了解析类信道模型中的前三阶散射模型和概率类信道模型中的MCS和MCI模型，并展望了这两类信道模型的未来研究方向。