基于生成对抗网络的MIMO信道估计方法

华郁秀，李荣鹏，赵志峰,2，吴建军，张宏纲

（1.浙江大学信息与电子工程学院，浙江 杭州 310027；2.之江实验室，浙江 杭州 311121；3.华为技术有限公司，上海 200120）

1 引言

为应对移动互联网和物联网爆炸式发展带来的千倍业务流量增长和海量设备连接，5G已经成为国内外移动通信领域的研究热点。业界普遍认为，5G 应该具备超高的能量效率和频谱效率，与4G 相比在传输速率、时延和用户体验方面也要有较大的性能提升。为实现5G 网络的关键性能指标，大规模多输入多输出（multiple input multiple output，MIMO）系统已经成为一项起基础支撑作用的关键技术。大规模MIMO 系统在基站或接入点上部署大量天线（可达数百个），提升了多个用户之间的复用能力，从而在不需要增加基站密度和带宽的条件下大幅度提高频谱效率。研究表明未来的6G为了实现太赫兹通信将会使用超大规模MIMO系统，收/发端会部署密集的天线阵列[1]，例如，为1 THz传输设计的超大规模MIMO收/发端的天线数量均为1 024[2]。未来社会很有可能是数据驱动的，6G网络将会是内生智能的[1]，因此学习高维信道数据分布并由此进行信道估计的生成对抗网络方法具有巨大的发挥空间。

大规模MIMO 依赖于空间多路复用，而空间多路复用又依赖于基站在上行和下行链路上都拥有准确的信道状态信息（channel state information，CSI）。上行链路获取CSI 比较容易实现，终端发送导频信号给基站，基站根据接收到的导频信号估计信道即可获取CSI。在下行链路中，CSI 的获取则较为复杂。一般来说，利用时分双工（time-division duplex，TDD）模式上下行的互易性可以获取下行链路信道的CSI。当然不排除频分双工（frequency-division duplex，FDD）模式适用于某些特定场景。后面的部分针对TDD 模型下的信道估计进行介绍。

信道估计方案大致可以归为非盲信道估计和盲信道估计。非盲信道估计（即基于导频的信道估计）需要借助收/发端都知道的参考信号（即导频），接收端通过接收到的导频信号进行信道估计。传统的基于导频的信道估计算法有最小二乘（least square，LS）和最小均方误差（minimum mean square error，MMSE）算法。使用导频进行信道估计会占用额外的时隙资源，有效的解决办法是通过尽量短的导频序列准确地估计信道。此外，通信环境中的高斯加性白噪声也会影响信道估计质量，因此如何在接收端减少接收到的导频信号中的噪声也是本文的研究内容。

2 相关研究

在关于大规模MIMO 系统中信道估计问题的研究中，基于导频的信道估计方法大多假设导频序列的长度Np大于或等于发射天线的数量Nt。如果不考虑TDD 模式的互易性，在对下行链路进行信道估计时导频序列的长度需要大于或等于基站的天线数量，对于大规模MIMO 系统中动辄几百的天线数量，所用的导频序列会大大占用无线资源，导致频谱效率降低。如果没有Np≥Nt这个假设，参考文献[3]证明了线性最小均方误差（linear MMSE，LMMSE）估计器的性能会大打折扣。而目前很多信道估计的方法是基于LMMSE 的[4-6]，所以Np≥Nt这个假设对于很多信道估计方法都是很有利的。但是在大规模MIMO 系统中，保证Np≥Nt这个假设成立是比较困难的，主要原因有3个。首先，为了确保Np≥Nt，大量的时间资源被用来发送导频，这将导致发送数据可以使用的时间资源有所减少，会进一步导致频谱效率降低。其次，信道估计方法的计算复杂度会随着Np的增加而增加。最后，Np≥Nt可能根本就不能实现，因为Np不能大于信道的相干时间（coherence time），这点通常是无法控制的。因此，在大规模MIMO 系统中，设计一种针对Np＜Nt的信道估计方案是非常有必要的。

近年来，深度学习在通信领域得到了广泛的关注，原因在于数据驱动的深度学习算法以其强大的函数拟合能力为很多缺乏有效模型的通信问题提供了潜在的解决方案[7-12]。针对上述的情况，近两年有研究工作利用深度学习算法设计信道估计器以解决这个问题。参考文献[13]采用编码器-解码器的结构进行信道估计，编码器包含一个双层神经网络，输入真实信道，输出接收端导频的估计，其中编码器的权重矩阵即导频矩阵。解码器由一个深度神经网络构成，负责从编码器的输出估计信道。参考文献[14]使用条件生成对抗网络（conditional generative adversarial network，CGAN）进行信道估计，其中生成器从基站接收到的导频信号中估计信道。该方法不仅可以处理Np＜Nt的情况，而且不需要特别设计导频序列。

另一方面，环境中的高斯白噪声也是影响信道估计质量的因素之一，因此在进行信道估计之前对接收端的导频信号进行去噪也可以提高估计质量。得益于卷积神经网络（convolutional neural network，CNN）在图像处理领域的优秀表现，越来越多的研究将基于CNN 的图像去噪算法应用到信道估计方法的设计中。这类的研究通常将接收端的导频矩阵和信道矩阵看作图片，其实数部分和虚数部分分别对应图片的两个通道。参考文献[8]使用DnCNN（denoising CNN）[15]通过监督学习的方式让神经网络从包含噪声的信道中学习到残差噪声，然后将粗估计得到的信道输入训练好的DnCNN 中得到残差噪声，最后将粗估计信道减去残差噪声就得到了更加精确的估计结果。类似地，参考文献[9]也使用了DnCNN 作为去噪网络对粗估计的信道进行处理，得到更加精准的估计。参考文献[16]也采用两个阶段进行信道估计，第一阶段通过DIP（deep image prior）[17]方法训练神经网络以实现对接收到的导频信号进行去噪；第二阶段将经过第一阶段去噪的接收端导频信号用于LS 估计器得到最终的信道估计结果。

总结来看，图像去噪技术用于信道估计主要有以下两种：在对信道进行粗估计后使用去噪网络；在信道估计前对接收到的导频信号进行去噪。前者用得比较多主要是因为有真实信道作为去噪网络的训练目标，基于监督学习的去噪算法（如DnCNN）可以达到很好的去噪效果，因而显著提高了估计信道的质量。而后者由于缺乏真实数据作为训练目标，因此很难使用DnCNN 这样的监督算法对接收端的导频信号进行去噪。参考文献[16]中使用的DIP算法是一种无监督学习的去噪算法，其主要利用了神经网络在学习含噪图像时先学会如何复制一张没有噪声的图像，然后才逐渐学会添加噪声。所以人为打断神经网络学习含噪图像的训练过程，就可以得到没有噪声的图像。因此参考文献[16]使用DIP 算法对接收端的导频信号进行去噪时就不需要使用额外的没有噪声的导频信号。但是DIP 算法没有给出关于中止训练的判断准则，这使得参考文献[16]的工作难以复现。

3 系统模型

大规模MIMO 系统的信道估计框架如图1所示，考虑单基站多用户场景下大规模MIMO 系统的上行信道估计问题。该场景中，基站上配备均匀线性阵列（uniform linear array，ULA），其中天线数量为M，基站覆盖的小区内分布着若干持有单天线设备的用户，数量为U。采用DeepMIMO 框架[18]生成基站和用户之间的信道数据。DeepMIMO 是专门为在毫米波和大规模MIMO 系统中使用机器/深度学习算法生成数据集的框架，其方便了研究人员对算法进行测试以及与其他算法进行比较（基于相同数据集）。DeepMIMO 是根据精确的光线追踪数据构建的，这些数据来自Remcom开发的光线追踪模拟器——Wireless InSite[19]。

图1 大规模MIMO系统的信道估计框架

具体地，在本文考虑的场景下，针对用户u和基站之间的第l条传输路径，光线追踪模拟器会计算以下信道参数：（1）基站侧的方位角和发射仰角（angles of departure，AoD）；（2）用户侧的方位角和到达仰角（angles of arrival，AoA）；（3）接收功率；（4）相位；（5）传输时延。这样就可以通过式（1）计算用户u和基站之间的信道向量：

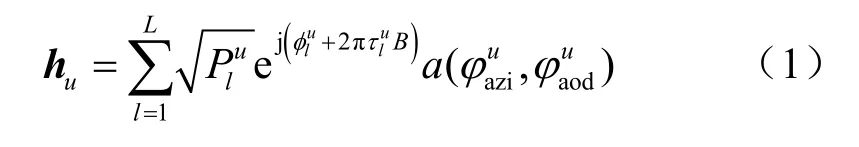
其中，L是传输路径的数量，B是系统带宽，表示基站的阵列响应向量，数学表达式为：

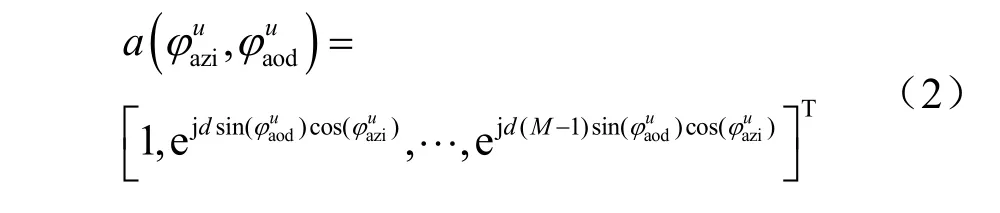
其中，d表示天线之间的距离。最后可以得到所有用户和基站之间的信道矩阵H∈CM×U为：

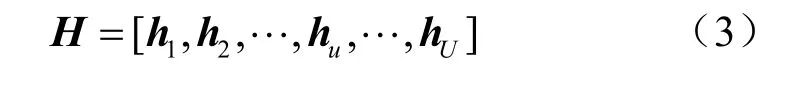
通过用户发送的导频信号在基站侧进行信道估计。假设U个用户同时发送长度为Np的导频序列给基站，本文定义Yc为接收端不含噪声的导频序列，数学表达式为：

其中 ，Φ∈CU×Np表示U个用户发送的导频序列构成导频矩阵，在这里考虑Np＜U的情况，所以无法保证导频矩阵行正交（即用户发送的导频序列两两正交）。此外，每个用户发送的导频序列是随意分配的，无须复杂的设计规则。通过Yc就可以得到基站接收到的导频信号Y∈CM×Np：

其中，N∈CM×Np表示采样自高斯分布的噪声矩阵。

基于导频的信道估计的目标就是最小化根据Y估计出来的信道矩阵与真实的信道矩阵H之间的误差。本文的方法会用到Yc和Y，为了简单起见，称Yc为“干净导频”，Y为“含噪导频”。此外，由于本文的信道估计方法不能处理复数变量，因此在后续描述算法时，将本节中出现的复数变量转化为图像。举例来说，Y∈CM×Np变成大小为M×Np×2的图像，其中，Y实数部分和虚数部分分别对应图像的两个通道。通过这样的变换，就可以用CNN处理这些数据，下一节将详细介绍N2N-GAN 信道估计方法。

4 基于GAN的两级信道估计模型

4.1 相关背景知识

（1）N2N去噪

图像去噪的目标是将含噪图像x = y + n中对图像质量有影响的噪声n去除，从而得到高质量的图像y。近些年来，CNN 被广泛用于图像去噪任务，但是这些基于CNN 的去噪算法在训练时通常需要含噪图像和对应的干净图像组成的成对数据。然而，当没有含噪图像对应的干净图像时，这些算法中的CNN 就没法得到训练，从而失去作用。针对这个问题，参考文献[20]提出了一个优雅的解决方案，那就是N2N去噪。不同于大多数去噪算法训练CNN学习含噪图像x到干净图像y的映射，N2N去噪只需要干净图像对应的包含独立噪声的含噪图像组成训练数据，即(y +n,y +n′)，然后训练CNN学习其中一张含噪图像到另一张含噪图像的映射。显然，由于噪声n和n′是相互独立的，N2N去噪不可能完美学习到含噪图片之间的映射关系。在这个不可能完成的任务上训练出来的神经网络可以得到与传统去噪算法采用干净图像训练出来的神经网络相同的去噪效果[20]。因此，在无法获得干净图像的情况下，N2N 只需要干净图像对应的包含独立噪声的含噪图像，即可训练神经网络达到很好的去噪效果。

（2）条件生成对抗网络

相较于其他生成模型，Goodfellow 提出的GAN[21]采用生成器和判别器博弈的方式学习到真实数据的分布。GAN 不要求预先假设真实数据的分布，这是GAN 最大的优势，同时也使得GAN 生成出来的样本太过自由。比如在手写数字数据集上训练好GAN，然后给生成器输入噪声，生成器就可以产生以假乱真的手写数字，但是生成器产生的数字是随机的，没办法控制。如果只想生成数字“1”，GAN 就无能为力了。为了解决GAN太过自由这个问题，研究人员提出了CGAN[22]。CGAN 在生成器和判别器的建模中均引入条件变量y，使用额外信息y对模型增加条件，可以指导数据生成过程。所以如果只想生成数字“1”，只要将手写数字图片的标签当作条件变量一同参与CGAN 的训练，在生成图片的时候设定条件变量为“1”，这样生成的图片就都是手写数字“1”。

在CGAN的生成器中，噪声z和条件信息y联合组成了输入。在判别器中，输入是真实数据x和条件信息y的联合或者生成器输出的合成数据G (z,y)。因此，CGAN 的目标函数如下：

（3）U-Net

在N2N-GAN 中，去噪网络和生成网络都用到了如图2所示的U-Net结构[23]。U-Net结构可以分为下采样和上采样，网络结构中只有卷积层和池化层，没有全连接层。在图2所示的U-Net结构中，左边从上到下为捕获上下文信息的收缩路径，右边从下到上为允许精确定位的对称拓展路径。U-Net 可以使用非常少的数据完成端到端的训练（即左边输入一张图像，右边输出一张图像）并获得很好的效果。U-Net的上采样阶段与下采样阶段采用了相同数量的卷积操作，且使用跳跃连接结构（图2中“复制”箭头）将下采样层与上采样层相连，使得下采样层提取到的特征可以直接传递到上采样层。

图2 U-Net结构示意图

4.2 N2N-GAN

N2N-GAN结构如图3所示，如前文所描述的，N2N-GAN信道估计方法包含两个阶段：阶段1负责对基站接收到的含噪导频图像进行去噪，阶段2利用去噪后的干净导频图像估计信道图像。

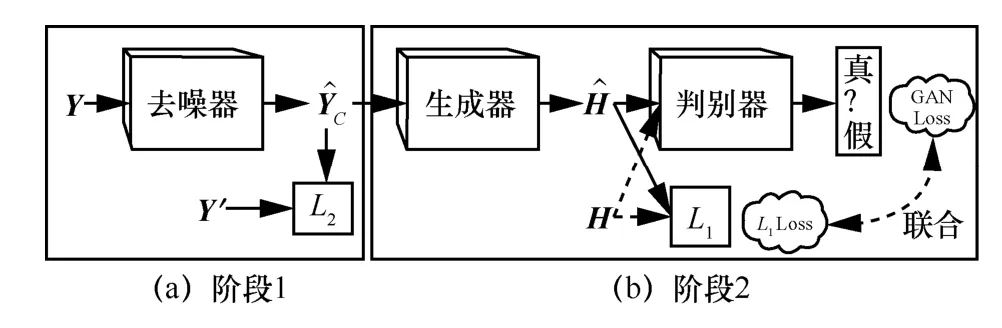
图3 N2N-GAN结构示意图

在阶段1中，部署了如图2所示的U-Net 作为去噪器，并采用N2N算法，即只用含噪导频图像进行训练。由于本文的训练数据集中包含一部分真实信道，因此定义了用户发送的导频矩阵，就可以使用式（4）构造接收端的干净导频信号，并将其作为训练数据集的一部分。在对去噪器的每一轮训练中，从训练数据集中随机选取一张干净导频图像（实际训练时采取批训练的方法，这里仅以批大小为1 举例说明），然后独立地采样两个与干净导频图像大小相同的高斯白噪声（噪声功率可以来自不同SNR 的情况）分别加到导频图像上，构成两张含噪导频图像Y和Y′。除了以上方法构造两张来自同一干净导频图像的含噪图像，在实际场景下，也可以在相干时间内（此时信道不变）多次发送导频信号，基站接收到的导频可视作来自同一干净导频的多个独立的含噪版本。有了两张含噪图像之后，将Y输入去噪器，得到Dnθ(Y)，其中，Dnθ(·)表示参数为θ的去噪器。为了训练去噪器，本文使用2 范数作为损失函数，可以表示为：

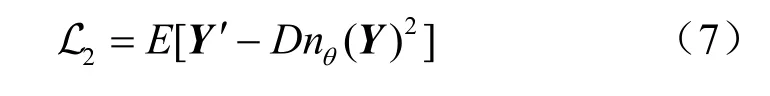
最后使用Adam 算法[24]训练去噪器。当训练完成之后，将测试数据集中的含噪导频图像输入去噪器，去噪器就会输出对应的去噪结果。

在阶段2的CGAN 中，生成器使用U-Net，判别器使用CNN。在训练阶段，生成器负责根据干净导频图像估计信道图像，判别器负责区分输入的是真实信道图像还是生成器产生的信道图像。在每一轮的训练中，从训练数据集中随机选取一张干净导频图像Yc输入生成器，生成器输出Gψ(Yc)，其中，Gψ(·)表示参数为ψ的生成器。然后将生成Yc的信道H和Gψ(Yc)输入参数为ω的判别器Dω(·)，判别器的输出表示输入是否为真实信道图像。该方法参考了图像处理领域很有影响力的pix2pix 算法[25]，与原始的CGAN有两点不同之处。首先Yc作为条件信息，在被输入生成器时没有加入噪声；其次，判别器在输入真实信道图像H时，没有同时输入条件信息Yc。此外，与参考文献[25]中的做法一样，为了让生成图像和真实图像在像素点上有所对应，还使用了1范数损失。因此，CGAN的损失函数包含以下两部分：

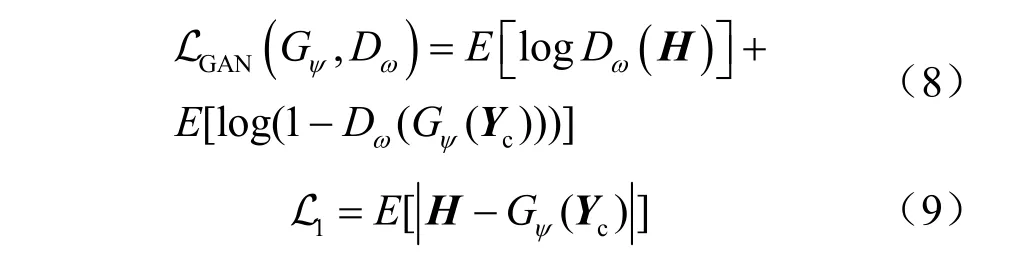
最终，得到CGAN的目标函数为：

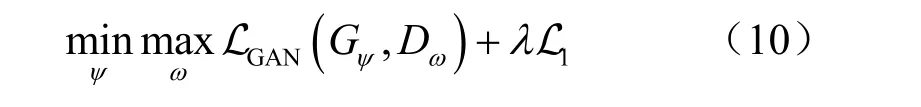
其中，λ为L1损失的重要性系数。当训练完成之后，将阶段1得到的去噪后的导频输入生成器，生成器就会输出对应信道的估计结果。

总的来说，阶段1和阶段2在训练时可以分开来并行训练，在部署使用时，基站收到的导频信号先被转化为图像，然后输入阶段1中的去噪器，接着去噪器将其输出馈送到阶段2的生成器，生成器输出估计的信道图像，最后将其转化成复数，得到估计信道。接下来通过仿真实验验证N2N-GAN的性能。

5 仿真验证

本节通过仿真验证N2N-GAN 在不同场景设定下的信道估计表现。参考文献[14]通过实验证明在直接由含噪导频估计信道的方法中CGAN 的准确度高于U-Net 和CNN，而且该工作也是考虑导频序列长度小于发射端天线数量的情况，具有一定的可比性。为了表述方便，将参考文献[14]中的信道估计方法称为端到端的CGAN 方法。本节主要考查N2N-GAN 两级信道估计方法和端到端的CGAN 估计方法以及传统的LS、MMSE信道估计算法之间的性能比较。

5.1 仿真数据与评估标准

首先，使用DeepMIMO 产生仿真所用的数据。光线追踪的场景为室内大规模MIMO场景，该场景为一个面积为10 m×10 m 的房间，房间内有两张桌子。天线均匀排布在天花板的一部分区域内，距离地面2.5 m。用户分布在房间一部分区域内，高度均为1 m。具体的仿真参数见表1。DeepMIMO 根据这些参数生成每个用户和天线阵列之间信道向量。用户发送的导频符号为，这些符号自由组合构成U个导频序列，这样就得到了U×Np的导频矩阵Ф。

表1 室内大规模MIMO 场景参数

随机选取32 个用户，将他们和天线阵列之间的信道向量拼接成矩阵。重复以上操作10 000次，就得到了真实信道的数据集。然后使用z-score 标准化方法处理数据集，处理后的数据集均值为0，标准差为1，更有利于神经网络的训练。接着利用式（4）和标准化处理后的真实信道数据生成干净导频，再通过叠加给定信噪比下的独立的高斯白噪声得到含噪导频。这样就得到了干净导频数据集以及含噪导频数据集。最后将3个数据集中的复数数据变成双通道的图像数据，再按照4:1的比例划分成训练集和测试集。仿真过程中使用干净信号叠加-10 dB到10 dB的SNR下的高斯白噪声生成多个含噪信号，由于它们都来源于同一个干净信号，所以可以将它们自由组合为成对数据，作为阶段1中的去噪网络的训练数据。阶段2中的CGAN直接使用干净信号作为生成器的输入，真实信道数据作为生成器所要学习的对象。通过这种方法，两个阶段的训练可以同时进行。作为对比的端到端的CGAN方法，使用含噪导频数据作为生成器的输入，生成器的学习对象同样是真实信道数据。

在仿真中，使用归一化均方误差（normalized mean square error，NMSE）为衡量估计信道Hˆ与H之间差异的评估标准，可以表达为：

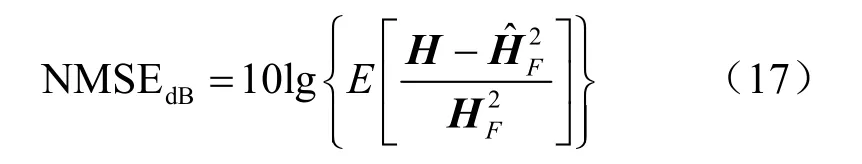
其中，||· ||F表示矩阵的F范数。为了方便观察仿真结果，将NMSE 转化为单位为dB的形式。

5.2 仿真结果分析

在定义了评估标准之后，首先比较不同SNR下N2N-GAN和端到端的CGAN以及传统的LS、MMSE算法之间的性能。由于LS和MMSE方法需要用户导频序列相互正交，所以此时设定导频序列长度和用户数量相等，且不同用户的导频序列保持正交。仿真结果如图4所示，图4中展示了信噪比从-10 dB变化到10 dB的过程中4种方法进行信道估计得到的MMSE值。从图4中可以看到，无论SNR和导频序列长度怎么变化，N2N-GAN的估计误差都小于端到端的CGAN。值得注意的是，当导频长度为8或16 以及SNR 较低的情况下，N2N-GAN的估计误差明显低于CGAN。此外，从图4可以看出，当导频长度减小时，两种方法的估计误差都会变大，N2N-GAN 的性能变化相对更加明显，并且N2N-GAN 在导频序列长度为4 时的性能和CGAN 在导频序列长度为16 时的性能相当。最后，从图4中可以看到传统的LS方法性能最差，MMSE方法的性能在 SNR 很高的情况下可以超越N2N-GAN，但在SNR较低时甚至比不上端到端的CGAN估计方法。

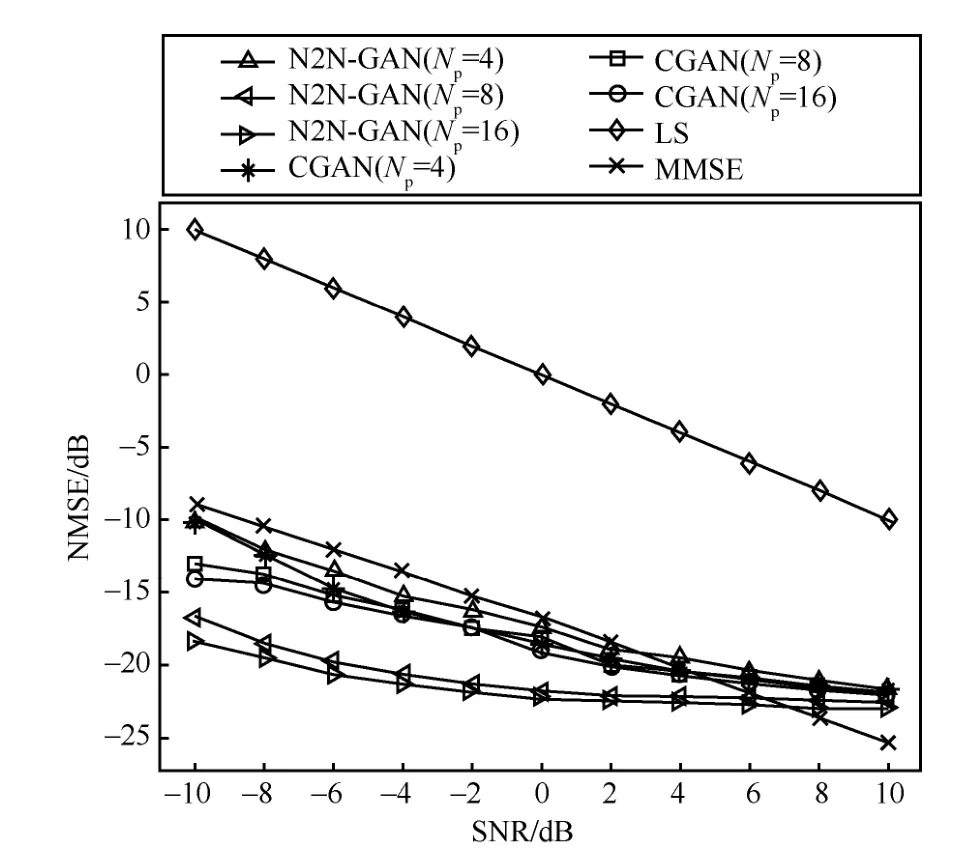
图4 不同SNR的情况下N2N-GAN和其他算法的性能比较

接下来考查N2N-GAN 在基站部署不同数量天线的情况下的估计性能，仿真结果如图5所示。在这个仿真中，设定SNR为0 dB。从图5中可以观察到随着基站天线数量的增加，N2N-GAN的估计误差不断减小，而基于CGAN 的估计方法则恰恰相反。基站天数数量的增加意味着信道矩阵的规模会变大，对于CGAN 而言，估计目标变得复杂，学习难度也相应增加，因此性能有所下降。而对于N2N-GAN 来说，阶段2的信道估计由于是无噪声估计的，性能几乎不会受输入输出规模的影响，但阶段1的去噪器却因为引入了更多的噪声信息从而学习到更好的去噪方式，所以N2N-GAN 的性能随着天线数量增加而有所提高。传统的LS方法的估计误差几乎不随天线数量的变化而变化，MMSE方法的性能随着天线数量的增加而降低。从图4和图5中可以看出，当导频序列长度从4增加到8时，N2N-GAN 的性能有明显的改善，但当导频长度从8增加到16时，性能增益并不明显。

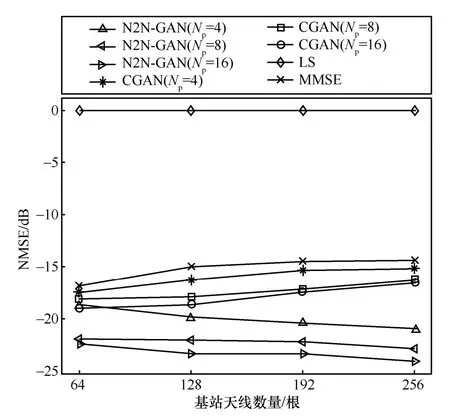
图5 不同算法的性能随基站天线数量变化的情况

6 结束语

在大规模MIMO 中，信道估计的准确率会直接影响通信系统的性能。本文着重研究导频序列长度小于发射天线数量情况下的信道估计问题，并通过去噪环节介绍接收到导频中的高斯白噪声。具体地，本文提出了基于生成对抗网络的两级信道估计方法，即N2N-GAN，其中阶段1负责对含噪导频进行去噪，阶段2根据去噪后导频信号估计信道。最后通过室内大规模MIMO 场景下的信道估计问题考查N2N-GAN的性能。仿真结果表明N2N-GAN 的估计误差随着SNR的增加而降低，且低于其他方法的估计误差。另外，随着导频序列长度的增加，N2N-GAN的性能也变得更好。当基站部署的天线数量增加时，N2N-GAN的估计误差有所降低，而其他方法的估计误差则呈相反的变化趋势。