模糊PID算法在婴儿培养箱解耦控制中的应用*

朱远帆， 杨海仕， 俞永伟， 王 琪， 胡燕海

(1.宁波大学 机械工程与力学学院，浙江 宁波 315211;2.宁波戴维医疗器械股份有限公司，浙江 宁波 315712)

0 引 言

婴儿培养箱为婴儿创造了一个类子宫的温湿度适宜的优良环境[1]，其中婴儿培养箱运行过程中对箱内温度及相对湿度的控制为核心环节。目前婴儿培养箱温湿度控制系统的研究动态中，传统的比例—积分—微分(proportional-integral-differential，PID)控制技术应用较为广泛，但对于像婴儿培养箱这种非线性、时变性[2]以及强耦合性的温湿度控制系统。

在控制发展的初步时期，研究人员将参考模型与多变量系统相结合的方式对对变量耦合系统进行解耦[3～5]。Garrido J等人在原多变量工业控制系统中加入设计好的解耦补偿器，把一个耦合多变量系统转换为多个无耦合的单变量子系统，一定程度上加强了控制器的相互适应能力从而提高了控制稳定性，但该方案所设计的解耦补偿器对于被控对象的数学模型精度极其依赖，对于非线性时变系统来说，控制精度难以保证。针对这一不足，Cheng W 等人[4]提出了一种融合了模糊控制和专家控制的控制方案，李爽[5]将神经元控制方法与模型参考方法相结合，但上述的方法没有利用解耦参考模型进行深度解耦，其本质只是增强单变量系统的自适应程度。文献[6]针对婴儿培养箱温湿度系统强耦合的问题，在传统PID控制的基础上，提出了前馈解耦方法，使控制稳定性及精度得到了较大提高。但根据婴儿培养箱安全专业要求GB11243—2008，湿度回路处于阶跃的状况下，温度回路的超调量必须小于标准范围。

为了解决该问题，本文提出将模糊PID控制器与解耦回路相结合的方法，采用专家系统对PID控制参数进行在线调整的优点，快速响应控制变量的变化，从而达到加强系统控制鲁棒性、自适应性并提高控制精度的目的。

1 婴儿培养箱温湿度控制系统建模

1.1 温湿度机理分析

图1为婴儿培养箱回风处理过程[7]。以加湿加温为例，外风W与内风N混合至C点，先经过加湿器加湿至L点，再由加温器加温至O点，后经鼓风电机传入婴儿小生境房内，从而使小生境房内的温湿度达到设定值。但其中加热器和加湿器主要执行设备运作过程中会同时对温度和湿度产生影响，如加湿器执行CL段加湿出理时，会产生加湿且降温作用，从而最终影响双回路控制精度，即温湿度耦合效应。

图1 婴儿培养箱回风处理过程

实际工程应用中，为了应对温湿度耦合效应，常采用限幅的工作方式应对，因存在着偶然性的因素，往往控制效果不够理想。

1.2 温湿度解耦控制模式设计

研究采用前馈解耦的控制思想，在控制器与被控对象之间加入一种校正装置，即前馈补偿数学模型[8]，从图2可以看出，控制与解耦由两个不同的控制器以对角传输的方式进行，从而从静态和动态上解决温湿度控制回路的耦合性。

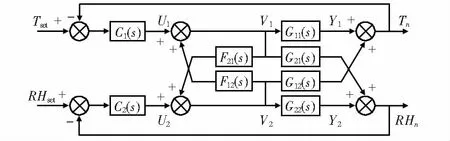
图2 婴儿培养箱温湿度前馈解耦模型原理

图2中，G(s)为传递矩阵，表示的是加热管加湿管分别对应温湿度的传递函数;F(s)为解耦补偿矩阵；C(s)为控制矩阵,则有

由原理图可得

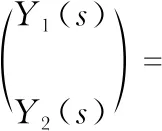
(1)

本文控制系统前馈解耦的目的就是温度不受加湿管的作用，湿度不受加热管的作用，因此要将系统模型部分更改成

(2)

将式(2)代入式(1)得解耦补偿器为

(3)

(4)

将补偿器模型代入式(2)得

W11(s)=G11(s)+F21(s)G12(s)

(5)

W22(s)=G22(s)+F12(s)G21(s)

(6)

控制器C1对温度回路产生影响的同时会对湿度产生一定干扰，若G21(s)传递函数效果较强，则对湿度控制的精度产生较大影响，甚至无法在短时间内到达稳态，同样控制器C2会对温度的精度产生较大影响。因此，本文引入解耦补偿矩阵F(s)，在传递矩阵前加入两个解耦补偿矩阵，使得耦合系统转换为两个相互独立的单回路系统，排除温湿度控制系统间的耦合性。

1.3 温湿度耦合控制对象模型建立

采用经典辨识方法取得模型参数，即对被控对象控制器施加一阶跃扰动信号，由传感器得到响应输出曲线后，根据实验得到的相关数据并借助线性拟合[9]的方式，求出各回路传递函数模型。

实验过程中采取如下措施：施加扰动信号前，将被控对象的初始工况调整在长期平稳运行阶段，从而得到稳定的被控对象运行状态；适当加大扰动次数，以减少随机干扰对测试产生的影响；3)适当减小扰动幅频，以避免控制对象非线性因素的增大。

首先取得较为稳定的外部环境，培养箱外室温为24 ℃，箱内的初始温湿度分别为28 ℃,60 %，并在较长时间内稳定不变。然后在加湿管断电情况下对加热管进行信号输入，将加热管的输出功率由20 %上升至50 %，直至培养箱内温度到达下一个稳定温度环境状态，全程收取传感器得到的温度数据，温度响应曲线由图3所示。

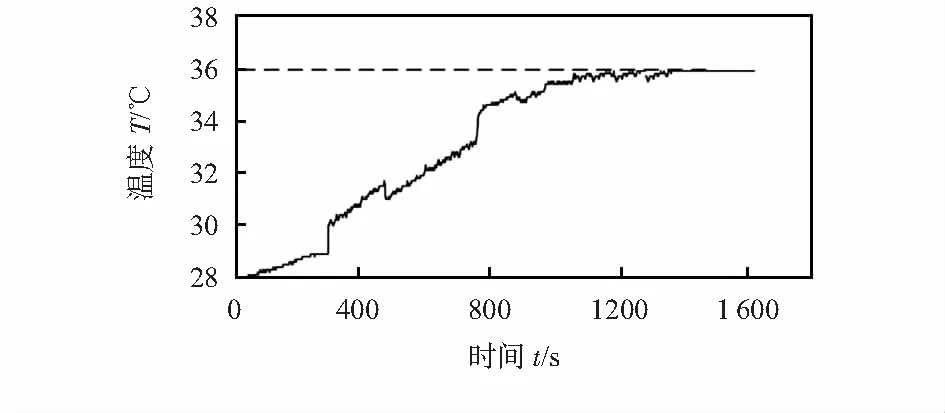
图3 加热管温度响应曲线

温度被控对象具有大时滞性、大惯性的特点，响应曲线表现为一条S形的非周期形曲线，其传递函数可用一个时滞环节和一个惯性环节串联的形式进行描述，如下式

(7)

由图3可知，温度从28.0 ℃开始，于36.1 ℃趋于稳定。根据一阶系统的阶跃响应两点法[10]求出放大倍数B如下

(8)

式中 ΔQ为加热比例增值30%。

代入两个不同时间点t1,t2，求出y*(t)所对应的值，即

1)当y*(t1)=0.4时，t1=1 035 s，y(t1)=31.16 ℃；

2)当y*(t2)=0.8时，t2=1 692 s，y(t2)=34.32 ℃。

将所求的两点t1,t2代入响应公式得T=598,τ=730。

整合以上阶跃响应参数，得到的加热管—温度的回路传递函数为

(9)

同理，利用以上阶跃响应两点法求得加热管—湿度回路、加湿管—温度回路、加湿管—湿度回路的三个独立传递函数为

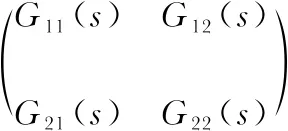
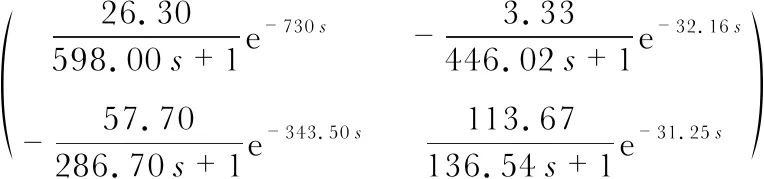
(10)

2 模糊PID控制器设计

模糊PID控制器结合了传统PID控制[11]和模糊控制，主要由模糊化处理、模糊推理及解模糊三部分组成[12]，如图4所示，模糊PID控制器在初始化参数kp0,ki0,kd0的基础上，通过计算实时系统误差e及误差变化率ec，通过专家经验和知识构建模糊控制规则表，并结合模糊论域对PID控制器的Δkp,Δki,Δkd从而形成模糊规律。

图4 模糊PID控制原理图

本文结合婴儿培养箱温湿度控制系统的而实际工作情况，以温度回路为例将输入变量和输出变量的模糊子集设定的七个级别为{负大、负中、负小、零、正小、正中、正大}，记{NB,NM,NS,ZO,PS,PM,PB}。

考虑到论域的鲁棒性、控制精度、计算灵敏度等因素，选用三角形隶属函数[13]为主隶属函数，表1为温度控制变量的基本论域、模糊子集、比例因子参数合集。

表1 温度回路模糊参数表

系统误差e及误差变化率ec对系统的影响通过固定其中一个值从而改变另一个值对婴儿培养箱温湿度系统的影响，通过实验，得到系统误差e及误差变化率ec的影响因素：1)增大e值，系统惯性越小，导致曲线变化速率越快;2)当e小于一定范围时，系统响应曲线上升减缓，收敛速度下降;3)当e超过一定范围时，系统响应曲线上升过快，超调量加大;4)增大ec值，系统的收敛速度降低，稳定性提高;5)当ec低于一定范围时，系统输出速率增大，出现超调或振荡;6) 当ec超过一定范围时，系统输出速率过慢，过渡时间增加。

根据e和ec对婴儿培养箱温湿度控制系统的温度回路影响分析，结合专家控制经验和Mandani推理方法[13]得到的温度回路模糊控制规则如表2所示。

表2 温度回路模糊控制规则表

3 仿真实验

为了验证本文采用的模糊PID控制器对于加入了前馈解耦的婴儿培养箱温湿度控制系统的运行效果，首先将传统PID算法引入到前馈解耦环节中，并将其与传统经典非解耦算法进行比较，观察解耦与非解耦的实际效果，然后再将改进的模糊PID算法加入到解耦系统中，最终对控制结果进行分析对比。

验证加入前馈解耦的控制效果的实验中，由于PID控制器调参因素对控制质量影响的重要性，研究通过Z—N调参与解耦矩阵相结合的调参方式，经过多次迭代后得到最良好的响应曲线，温湿度回路的控制参数Kp0，Ki0，Kd0分别为1.432 0，0.000 881，133.646 2及0.247 5，0.000 979,15.659 4。本研究针对非解耦回路采用的调参方法为传统临界比例调参[14]，得到的控制初始化参数Kp0，Ti0，Td0分别为1.764 7，320，80及0.4211，220，55。根据婴儿培养箱安全专业要求GB11243—2008[15]并考虑到婴儿培养箱在医院的工作环境因素，将温度回路的初始温度设定为32 ℃，初始湿度设定为60 %，两参数均为30 s采样一次，总仿真时间为10 000 s，其中在5 000 s时间时将湿度上升至80 %，在8 000 s时间时将温度上升至36 ℃。得到的控制过程响应曲线如图5所示。

图5 仿真曲线

表3结果为三者性能比较。

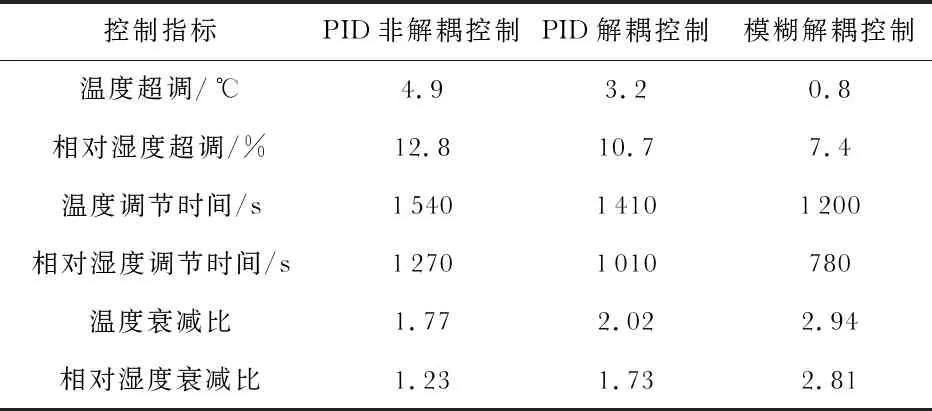
表3 温湿度控制系统仿真性能比较

从非解耦条件下的温湿度仿真曲线图5可以看出，由于温湿度耦合的作用，传统的调参方式无法取消两个回路间的影响。当5 000 s左右和8 000 s左右，给控制器施加响应信号后，温度调节时间达到了1 540 s，相对湿度调节时间达到了1 270 s，超调量也超出了婴儿培养箱的校准范围，出现耦合特性后的系统控制效果不够理想。为了消除温湿度间耦合关系，本文研究采用加入前馈解耦控制结果如图5(b)所示，从结果可以看出，稳定状态下，双回路间的影响基本得到解决，调节时间和超调有所减少，系统动态响应有所改善。

从图5(c)本文提出的基于模糊PID的解耦仿真曲线图可得，与文献[6]所提出的将前馈补偿器与传统的PID控制器相结合的控制方式相比，温度和湿度的超调分别减小到0.8 ℃和7.4 %，温湿度调节时间减小了190 s和230 s，平均下降比约为18 %，从而证明了模糊PID控制器能够更好地完成婴儿培养箱温度和相对湿度地解耦，并在调节时间和调节量等控制指标方面均有所改善。

4 结 论

采用阶跃响应法进行温湿度双回路的模型分析;针对加入了前馈解耦的双回路自适应度不足的问题，结合模糊PID控制的在先调整能力强的优点，使温湿度耦合回路智能化;最终实现婴儿培养箱温湿度控制系统的动态解耦。

对仿真结果进行进一步分析表明：本文建立的模糊PID控制器在双回路解耦系统中的动态响应、稳定性及控制精度均优于传统PID控制器，前者在调节时间及超调量等控制指标方面均有所改善。基于前馈解耦的模糊PID控制系统的温湿度回路超调分别为0.8 ℃，7.4 %，温度回路的调节时间为1 200 s，相对湿度回路的调节时间为780 s。当箱内温度或相对湿度突然阶跃时，基于前馈解耦的模糊PID控制系统具有较强的稳定性及适应性。因此，本文研究的解耦控制方法对婴儿培养箱温湿度控制具有一定的应用价值。