基于双通道卷积神经网络的交通标志识别算法*

孔月瑶， 严 群， 姚剑敏， 林志贤

(福州大学 物理与信息工程学院，福建 福州 350108)

0 引 言

交通标志识别与先进驾驶辅助系统(advanced driver assistance system,ADAS)和无人驾驶紧密相关，该领域一直是国内外专家研究的热门课题[1]。然而计算机在对自然场景下交通标志图像的采集过程中会受到很多因素的干扰，导致采集到的图像不清晰甚至变形从而影响识别。同时，交通识别系统必须快速识别并及时反馈给驾驶员，否则不但起不到辅助作用还会造成危险。因此，如何在复杂的自然场景下快速并准确地识别交通标志非常重要。

随着深度学习算法发展，卷积神经网络(convliutional neural network,CNN)已成为人工智能领域中用于对象分类和模式识别应用的突破性技术[2]，如车型识别[3]，语音识别[4]等。越来越多研究学者将其用于交通标志识别系统。Ciresan D等人提出使用多列CNN进行组合[5]，获得99.46 %的准确率，但需要4块图形处理单元(graphics processing unit,GPU)训练37 h。文献[6]提出将分割出的交通标志感兴趣区域(region of interest,RoI)输入到CNN进行识别，虽然减小了天气等因素的影响，但稳定性较差。文献[7]提出使用逐层贪婪预训练和支持向量机(support vector machine,SVM)作为分类器来优化CNN，但是不能保证其泛化性能。

针对上述算法的不足，本文提出一种新的网络模型，结合单通道卷积神经网络中特征单一及梯度弥散的问题，提出采用非对称双通道作为输入，两通道采用不同的网络结构来获取丰富的特征；同时在上层通路采用跃层连接，将浅层和深层特征进行融合，防止信息丢失；最后在全连接层将两通道的输出特征进行融合。实验结果表明，本文算法能有效减少训练时间并提高准确率。

1 CNN

CNN本质上是一个多层感知机[8]，可以通过某种方式将输入的非线性可分数据映射到高维空间，再使用线性分类器完成分类。它采用局部连接和共享权值的方式，一方面减少权值的数量使网络更易于优化，另一方面降低了网络的复杂度。CNN包括卷积层、池化层和全连接层。

卷积层主要用来进行特征提取。卷积层通过可训练的卷积核K，对输入的二维图像I进行卷积操作，并通过激活函数得到该层的输出特征图S。对图像进行卷积操作的数学表达式为

S(i,j)=(I×K)(i,j)=∑∑I(m,n)K(i-m,j-n)

(1)

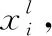
(2)

式中p为池化窗口大小，s为步长。全连接层在卷积网络中起到分类器的作用，卷积层和池化层等操作将多维的低级特征组合成高级特征，并映射到隐层特征空间后，全连接层将学到的分布式特征表示映射到样本标记空间，最后对这些特征进行分类，以达到对图像分类的效果。

2 交通标志识别算法

2.1 图像增强

由于自然场景下的交通标志极易受到天气、光照和环境等影响，因此，采用合适的图像增强算法来突出图像的特征信息是非常必要的，本文采用直方图均衡化对图像进行增强。首先对图像中像素灰度级ri进行归一化处理,则0≤ri≤1,i=0, 1, 2, …,n-1，其中ri=0时表示黑,ri=1时表示白。每个像素值在[0，1]的灰度级是随机的，用P(ri)来表示图像灰度级的分布情况，则第i个灰度级出现的概率为P(ri)=ni/n，其中ni为图像中灰度为ri的像素数，n为图像的像素总数，图像进行直方图均衡化的函数表达式为

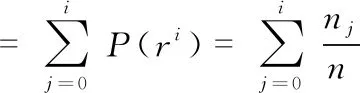
0≤ri≤1,i=0, 1, …,n-1

(3)

由此可见，si在其定义域范围内的概率密度是均匀分布的，即图像经增强后可达到均衡。

2.2 非对称双通道CNN

在CNN中，较浅的卷积层通常学到的是图像局部边缘特征，如边缘和颜色等，有助于在复杂背景下区分出目标，而更深的卷积层则捕获更高级的抽象特征，这些抽象特征对目标分类非常有利。在网络中，提取的浅层特征信息在经过多个卷积层和池化层后，逐层映射为深层特征信息，但部分浅层特征信息丢失，仅使用这些抽象特征进行分类，构造的不是最优的分类器；另外，随着网络层数的加深，神经网络易产生梯度弥散问题，导致网络训练困难[9]。针对上述单通道CNN的问题，本文提出非对称双通道CNN结构，可以避免梯度弥散问题，并加入DenseNet[10]中跃层连接的方式，对底层得到的浅层特征进行复用。两通路最后得到的特征在全连接层进行融合，并通过SoftMax分类器进行分类。图1为非对称双通道CNN结构。其中,C代表卷积层，p代表池化层。

图1 非对称双通道CNN结构

通路1主要用来提取图像的浅层特征，大卷积核可以提取更具全局特性的特征，避免重要的边缘、颜色等特征信息丢失，通路1输出一维特征向量：P2=[1，A2×A2×M2]，并且通路1中的p1层的连接方式与其他层不同，它继续进行卷积计算的同时也将提取的特征信息展开为一维向量P1=[1，A1×A1×M1]，并使用跃层连接的方式，跨越中间层直接输入到全连接层，使其提取的浅层特征与fv层输出的深层特征在全连接层进行融合，防止浅层信息丢失。

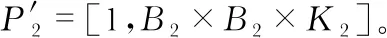
此外，本文采用LReLUs(Leak ReLUs)代替常用的ReLU激活函数。虽然使用ReLU进行训练比tanh或Sigmoid单位更快，但ReLU很脆弱，在训练期间可能会死亡。由图2(a)可知，对于小于0的值，这个神经元的梯度一直是0，如果学习率很大时，很可能会造成网络中较多的神经元‘dead’。而LReLUs正可以修复这个的问题。LReLUs的数学表达式如(4)所示，这里α是一个很小的常数，这样保留了一些负轴的值，使负轴的信息不会全部丢失。文献[11]也证明了在CNN中使用LReLUs的性能优于ReLU。实验结果发现，使用LReLUs在GTSRB数据集上实现了比ReLU约高2 %的准确度。图2显示了ReLU和LReLUs的功能公式(4)如下

图2 ReLU和LReLUs的功能

y=max(0,x)+αmin(0,x)

(4)

3 实 验

3.1 数据集准备

本实验使用德国交通标志识别基准(German Traffic Sign Recognition Benchmark，GTSRB)，该数据集包括43类交通标志，其中训练集图片39 209张，测试集图片12 630张。图3为GTSRB中随机抽取每类的图片。通过研究数据集的特性，选择不同的数据增强方式，对数量少的类别采用旋转(-15°,15°)及左右平移的方式，数量多的类别仅进行旋转，使所有的类别在增加数量的同时达到平衡。使用数据增强后，训练集达到100 469张，测试集保持不变。

图3 GTSRB中随机抽取每类的图片

3.2 实验结果与分析

实验使用的计算机配置为i5—8500U处理器，GTX 1080显卡，内存16 G。使用TensorFlow训练网络，其中优化器采用Adam Optimizer，学习率设为0.000 1，最大迭代次数设为200。

为了验证本文提出的网络结构在交通标志识别上的性能，本文设置了4组实验进行分析：

1)选取输入网络的最佳尺寸。GTSRB数据集中的图片大小不一，但是对于神经网络来说，输入节点个数是固定的，因此，需要将图片统一尺寸后再输入到网络中。为了确定输入的最佳尺寸，实验保持其他参数不变，并使用4个不同尺寸的GTSRB数据集对网络进行训练及测试，最后通过对比分析，确定输入网络的最佳尺寸为48×48。实验结果如表1所示。

表1 不同输入尺寸的准确率

2)验证使用激活函数LReLUs是否能有效提高准确率。主要将其与ReLU在训练时间及准确率方面进行对比。表2表明，LReLUs代替ReLU激活函数能有效的提高交通标志识别准确率。

表2 ReLU与LReLUs的效果

3)验证双通道网络模型在GTSRB上的效果。首先，通过对训练过程中的精度和损失曲线可视化，分析其训练的动态过程。图4分别表示单通道网络模型(参数一致)和双通道网络模型在训练过程中对应的识别率和损失曲线。两组模型的最大迭代次数都为200，由图4可看出，两组模型都在迭代一定次数后趋于平稳，其中单通道网络模型在迭代120～130次达到平稳状态，此时损失值接近0，准确率约为96 %；而提出的模型在迭代70～80次后损失值接近0，准确率趋近1，网络达到平稳。由此可以看出提出的模型收敛速度更快，并且达到更高的准确率。

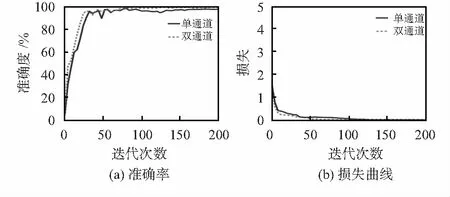
图4 准确率和损失曲线对比

表3列举了不同算法在GTSRB数据集上的训练时间及准确率。由表3可知，本文提出的算法比人工神经网络(artificial neural network,ANN)、AlexNet算法的识别率都要高，训练时间也大大减少，虽然识别率比文献[7]略低，但是其识别单张图片的时间是它的0.1倍左右。本文提出的算法准确率达到97.89 %，且识别单张图片只要14 ms，相比其他算法有一定的优势。

表3 不同算法在GTSRB上的效果对比

4)验证本文算法在实际情况下的识别效果。选取实际场景中质量差的交通标志图像进行测试。本文通过复现

AlexNet网络和文献[12]提出的改进CNN算法，对下面4种情况下的图片进行测试，并与本文提出的算法进行对比,实验结果如表4所示

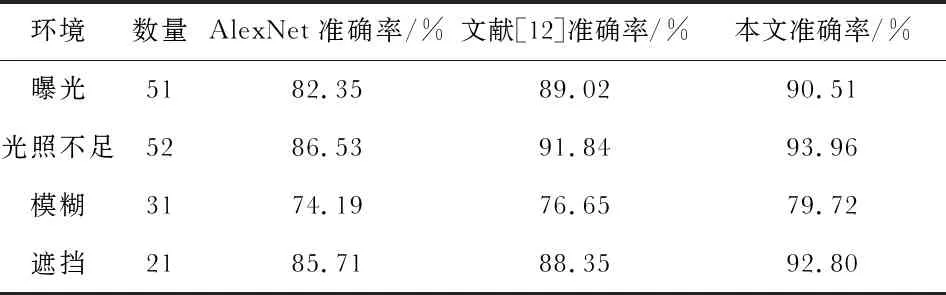
表4 不同算法在复杂环境下的识别率

由表4的测试结果可以看出，在这四种实际的复杂环境下，本文提出的算法的识别准确率比另外两种算法的表现都要好，且能达到较高的识别水平，其中，在光照不足条件下表现的最佳，但对模糊的图像识别能力略差，还有待提高。总体来说，该算法具有良好的分类能力。

4 结束语

本文设计并实现了基于双通道CNN的交通标志识别算法，主要通过两个不同的网络通道来提取不同的特征，并在全连接层进行融合以提取更丰富的特征信息，同时在提取边缘信息的上层通道添加跃层连接避免浅层特征丢失，最后使用LReLUs代替ReLU，提高准确率。

多次实验结果表明：本文算法在GTSRB上和实际环境下都能取得较好的识别率，具有一定的鲁棒性；算法在保证准确率的同时提高了训练速度，符合交通标志识别系统的准确性和实时性。