高斯色噪声下基于2q阶嵌套MIMO阵列的DOA估计算法*

吴 琼， 李兆展， 林艳红， 胡国平， 周 豪

(1.中国人民解放军93861部队，陕西 三原 713800；2.空军工程大学 防空反导学院， 陕西 西安 710051)

0 引 言

波达方向(direction of arrival, DOA)估计在雷达、声纳以及通信等领域有着广泛的应用，学者们相继提出了多重信号分类(multiple signal classification,MUSIC)算法和基于旋转不变技术估计信号参数(estimating signal parameters via rotational invariance techniques，ESPRIT)算法等经典的DOA估计算法。为便于研究，经典的DOA估计算法常假设接收的噪声是高斯白噪声[1,2]，但这在现实的电磁环境中难以满足，实际接收的噪声可能是高斯色噪声，此时经典DOA估计算法的性能将下降甚至失效[3]。针对这一问题，先后提出了空间差分算法、预白化算法、高阶累积量算法等。其中，文献[4,5]针对相干和独立信源在高斯色噪声下的DOA估计问题，利用噪声协方差矩阵满足Toeplitz矩阵结构的特点，通过空间差分算法消除色噪声的影响。然而，空间差分算法只适用于相干和独立信源共存的条件下，当仅存在独立信源时，算法将失效。文献[6]基于仅含色噪声的采样数据对阵列接收信号进行预白化，使色噪声变为白噪声，以便后续的DOA估计。但在实际测向时，仅含色噪声的数据难以取得，因此该算法的实用性不够强。高斯噪声的四阶以上累积量为零，利用这一特性可有效消除高斯色噪声的影响。文献[7]提出一种基于四阶累积量的Toeplitz矩阵重构算法，在高斯色噪声和弱信噪比条件下仍然具有较高的估计精度。文献[8]利用多输入多输出(multi-input multi-output,MIMO)雷达的旋转不变性构造四阶累积量矩阵来消除高斯色噪声，并利用PM算法估计DOA。文献[9]提出了具有高分辨率的2qMUSIC算法。然而，这些算法均基于均匀密布线阵，阵元有效自由度仍有提升空间。针对上述问题，Pal等人将高阶累积量与嵌套阵相结合，提出基于高阶累积量的2q阶嵌套阵[10]，在显著扩展阵列有效自由度(degree of freedom,DOF)的同时抑制了高斯色噪声，实现了色噪声条件下的高精度DOA估计。然而，其2q阶嵌套阵对应的“差联合阵列”存在一定的孔洞，当应用MUSIC等算法时，仅能使用其中连续阵元，而离散的阵元被浪费。

对此，本文利用MIMO雷达能够形成“和差联合阵列”的特点，提出一种基于高阶累积量的2q阶嵌套MIMO阵列，提高了有效自由度，从而实现更高精度的DOA估计。

1 高阶累积量

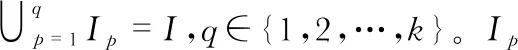
(1)

式中cx(I)为随机变量x1,x2,…,xk的r阶累积量，mx(Ip)为其符号集为Ip的矩。

若x1,x2,…,xk均为零均值随机变量，则式(1)将大为简化。以四阶累积量为例，根据式(1)有

c4x(x1,…,x4)=E{x1x2x3x4}-E{x1x2}E{x3x4}-

E{x1x3}E{x2x4}-E{x1x4}E{x2x3}

(2)

对于零均值的高斯随机过程，其二阶累积量和二阶矩均等于其方差σ2，其高阶(三阶及三阶以上)累积量恒为零。因此，当信源为非高斯分布而噪声为高斯分布时，可利用高阶累积量算法来消除高斯噪声[9～12]。

2 基于高阶累积量的2q阶嵌套MIMO阵列

文献[11]提出一种基于高阶累积量的2q阶嵌套阵，通过计算高阶累积量矩阵并矢量化构造虚拟2q阶“差联合阵列”，从而实现自由度的扩展。以N=8的四阶嵌套阵(q=2)为例，其物理阵元位置如图1(a)所示，为[0,1,2,5,8,17,26,53]，对应的虚拟阵列阵元位置如图1(b)所示。可见2q阶嵌套阵列能够用较少的阵元实现较高的自由度，相应的角度估计性能也将得到提高。然而，从图1(b1)也可看到，虚拟阵列并非是连续的，在82,83,86,91,92,94,95等处存在间断，而常用的MUSIC,ESPRIT等算法均要求阵列为连续阵，因此,正半轴间断点81右边的这些有效自由度难以利用，造成了有效自由度的浪费。

由图1(b)分析可知，2q阶嵌套阵利用构造高阶累积量和矢量化形成虚拟的“差联合阵列”，使自由度得到了扩展。然而，其仅仅是针对接收阵进行了优化，并未将自由度扩展的潜力充分发挥出来。

图1 8阵元四阶嵌套阵物理位置及其对应的虚拟阵列示意

MIMO雷达能够发射正交波形，并在接收端通过匹配滤波形成“和联合阵列”，从而扩展接收阵虚拟孔径[13]。受到这一启发，提出一种2q阶嵌套MIMO阵列。首先利用MIMO雷达匹配滤波特性将自由度加以扩展，随后再对接收数据构造高阶累积量协方差矩阵并矢量化，形成2q阶“和差联合阵列”，从而进一步扩展有效自由度。

设2q阶嵌套MIMO阵列的阵元数为N，由于接收阵列原点处需要放置一个参考阵元，因此，只需考虑对余下的N0=N-1个阵元的位置进行优化即可。而根据文献[11]，仅考虑接收的情况下，可将N0个阵元划分为2q阶子阵，各阶子阵的阵元个数为

(3)

式中m和n分别为N0+2q-1除以2q所得的除数和余数，即

N0+2q-1=2qm+n0≤n≤2q-1

(4)

对于第一阶至第2q-1阶子阵，各子阵中阵元的坐标位置为

(5)

而第2q阶子阵的阵元位置为

(6)

由于MIMO雷达能够通过接收端的匹配滤波形成“和联合阵列”，在第二步计算高阶累积量并矢量化过程中能形成“差联合阵列”，因此，为了使最终的“和差联合阵列”自由度尽可能大，应使式(5)和式(6)中的阵元之和最大，且形成的连续虚拟阵元尽可能多。为此，将N0中前N0-1个阵元按照式(5)和式(6)计算出的位置置于发射阵列，将最后一个阵元按第2q阶子阵中最后一个阵元的位置，放置在接收阵中。以8阵元的四阶(q=2)嵌套MIMO阵列为例，发射阵和接收阵的结构如图2所示，其中发射阵元的位置为[0,1,2,5,8,17]，接收阵元的位置为[0,35]。对应的虚拟“和差联合阵列”的阵元位置如图3所示。

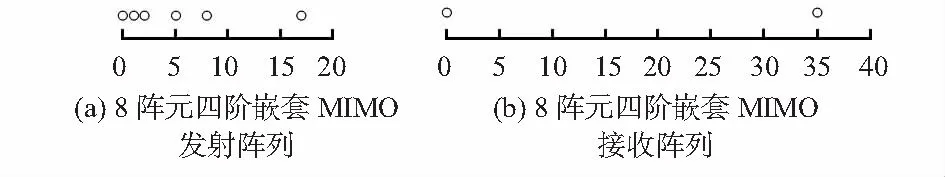
图2 8阵元四阶(q=2)嵌套MIMO物理阵元位置

图3 8阵元四阶(q=2)嵌套MIMO阵列对应的虚拟阵列示意

通过对比图1(b)和图3可发现，8阵元的四阶嵌套MIMO阵列将形成更多的连续阵元；此外，8阵元四阶嵌套阵的总自由度为197，而8阵元四阶嵌套MIMO阵的总自由度为209。因此，无论从连续阵元数还是总自由度来看，8阵元四阶嵌套MIMO阵列都更有优势，能够实现更高精度的DOA估计。

3 基于空间平滑的MUSIC算法

2q阶嵌套MIMO阵列匹配滤波后的信号为

y(t)=[ar(θ1)⊗at(θ1),…,ar(θk)⊗at(θk)]s(t)+w(t)

=(Ar∘At)s(t)+w(t)

=As(t)+w(t)

(7)

式中Ar∘At为Ar和At的Khatri-Rao积，w(t)为匹配滤波后的噪声，s(t)为目标反射系数组成的向量

s(t)=[ξ1(t),ξ2(t),…，ξk(t)]T

(8)

A=Ar∘At=[a(θ1),a(θ2),…,a(θk)]

(9)

其中,接收到的目标反射信号ξk(t)(k=1,2,…，K)假设为非高斯分布，且噪声w(t)为高斯色噪声。A为匹配滤波后形成的虚拟导向矢量矩阵，相当于发射阵列和接收阵列的“和联合阵列”

atr(θk)=[ejdtr1πsin θk,ejdtr2πsin θk,…，ejdtrMNπsin θk]T

(10)

式中dtr((n-1)M+m)=dtm+drn由于接收阵元间距足够大，MN个虚拟阵元的位置dtr((n-1)M+m)各不相同。

利用式(2)计算y(t)中元素的高阶累积量并排列为一个(MN)q×(MN)q的2q阶Hermitian矩阵。当q≥2时，该矩阵的排列方式不止一种，用C2q,y(l)(0≤l≤q-1)代表不同排列方式的累积量矩阵，则有

[atr(θk)⊗ l⊗atr(θk)*⊗(q-l)]H+

(11)

(12)

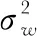
cvec=vec[C2q,y(l)]

(13)

(14)

(15)

(16)

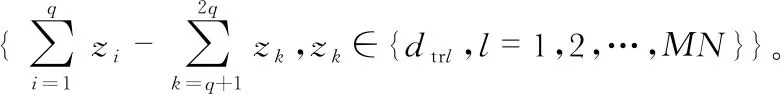
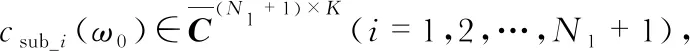
利用式(17)计算协方差矩阵并求平均可得

(17)

最后，基于C′可采用MUSIC,ESPRIT等算法来估计DOA。

4 仿真实验

通过Monte Carlo仿真验证所提算法的有效性。设总阵元数为8，Monte Carlo仿真次数为500。为便于计算分析，仿真中取q=2。

仿真一多目标性能

首先分析多目标条件下的DOA估计性能，设K=15个目标以10°为间隔分布在-70°到70°的空域，SNR=10 dB，快拍数L=300，图4所示为2q阶MUSIC算法(记为2qMUSIC)、基于2q阶嵌套阵的DOA算法(记为2qNA)和基于2q阶嵌套MIMO阵列的DOA算法(记为2qNA MIMO)对应的空间谱。而空间差分MUSIC算法和最基本的MUSIC算法由于最多只能估计N-1个目标，因而在这种条件下失效，故不再在图4中进行展示。由图4可见，只有基于2q阶嵌套MIMO阵列的DOA算法能够准确估计出所有15个目标的角度，从而证明与2q阶嵌套阵相比，2q阶嵌套MIMO阵列的自由度得到了提高。

图4 不同算法对15个目标角度估计

仿真二邻近目标性能

随后分析各算法对邻近目标的角度估计性能，设K=2个目标的角度分别为10°和10.2°，SNR=10 dB，快拍数L=300，图5所示为2q阶MUSIC算法、基于2q阶嵌套阵的DOA算法和基于2q阶嵌套MIMO阵列的DOA算法对应的空间谱。由图5可见，只有基于2q阶嵌套MIMO阵列的DOA算法能够准确将两个邻近目标区分开，而基于2q阶嵌套阵的DOA算法和2q阶MUSIC算法均失效，从而进一步证明了2q阶嵌套MIMO阵列自由度得到了提高。

图5 不同算法对两个邻近目标角度估计

仿真三高斯色噪声下性能

仿真三是为了研究2q阶MUSIC算法、基于2q阶嵌套阵的DOA算法和基于2q阶嵌套MIMO阵列的DOA算法在不同快拍数和不同信噪比下的测向性能。为此定义均方根误差(root mean square error,RMSE)为

(18)

图6(a)所示为不同算法的RMSE随信噪比的变化关系，其中快拍数L=300，K=4个目标的角度分别为[10°,20°,30°,40°]。由图6(a)可见，在快拍数一定的情况下，不同算法的RMSE均随着SNR的增大而降低，其中基于2q阶嵌套MIMO阵列的DOA算法的估计精度最高，这是因为，一方面其采用了高阶累积量消除了高斯色噪声的影响，另一方面通过将2q阶嵌套阵与MIMO相结合实现了有效自由度的提高。

随后研究不同算法的RMSE随快拍数的变化关系，其中信噪比设为10 dB，K=4个目标的角度分别为[10°,20°,30°,40°]。由图6(b)可见，在信噪比一定的条件下，不同算法的RMSE均随着快拍数的增大而降低，其中2q阶嵌套MIMO阵列的估计精度最高，而MUSIC算法由于没有针对色噪声采取有效抑制，因而其估计精度最低。

图6 不同算法RMSE随信噪比和快拍数变化情况

5 结 论

本文针对高斯色噪声下2q阶嵌套阵的虚拟中存在孔洞，自由度利用不充分的问题，将2q阶嵌套阵与MIMO体制相结合，构造2q阶嵌套MIMO阵列，从而有效提高了形成的虚拟阵列中连续阵元的个数，且能够有效消除高斯色噪声的不利影响。仿真表明:与2q阶MUSIC算法和基于2q阶嵌套阵的DOA算法相比，基于2q阶嵌套MIMO阵列的DOA算法的多目标分辨力、邻近目标分辨力均有所提高，在相同信噪比或相同快拍数下的估计精度也高于2q阶MUSIC算法和基于2q阶嵌套阵的DOA算法。