结合混沌的长相关锂电池寿命预测方法
王海洋, 宋万清
(上海工程技术大学 电子电气工程学院,上海 201600)
0 引 言
锂电池的剩余寿命预测一直是其可靠性分析和健康状态预测中一个重要的研究方向[1]。更加准确的锂电池预测对于其使用的安全性、可靠性以及减少经济损耗等都有着十分重要的作用[2]。在过去的几十年里,各种RUL预测方法被提出,例如:物理原理法、实验法、数据驱动法以及混合法[3]、基于自回归滑动平均(auto-regressive moving average,ARMA)时间序列的预测模型法。陶耀东等人[4]利用Box-Jenkins ARIMA 模型模拟锂电池退化过程从而进行锂电池的RUL预测研究。而王巍等人[5]则提出了新的高斯过程回归方法提升训练和预测的速度。基于人工神经网络的锂电池RUL预测也是目前研究的热点。文献[6]在进行的锂电池RUL预测研究时则提出一种利用重采样来对前馈神经网络进行输入选择的新思路。陈雄姿等人[7]便提出了一种基于贝叶斯最小二乘—支持向量回归(least square support vector regression,LS-SVR)的锂电池剩余寿命在线概率性预测方法。而王春雷等人[8]则利用改进的相关向量机方法进行锂电池RUL预测。
本文结合混沌理论得到锂电池最大预测时间尺度,再利用具有长相关性的FARIMA 模型应用于锂电池剩余使用寿命预测,通过计算Hurst指数建立起预测模型,并给出RUL预测具体的步骤与其概率密度函数计算公式。最终通过实际的美国NASA Amse数据库中的锂电池退化数据进行实际的RUL预测实验,并选择多种误差标准量化其预测结果。
1 混沌理论
混沌理论属于非线性学科的一种,科学界认为万物皆是混沌构成。因此对于混沌的研究方面设计自然与人文科学的各个方面[9]。混沌理论的发展主要归功于1963年洛伦兹的论文发表。本文结合混沌动力学理论,通过计算Lyapunov指数给出的可预测剩余寿命的最大尺度,从而优化RUL预测过程,获得更好的预测结果。计算Lyapunov指数的方法有:定义法、Wolf法、Jacobian方法、P—范数法、小数据量法等。本文选在实际应用中比较有效的Jacobian法,其具体计算步骤如下:
考虑下列微分方程系统为
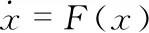
(1)
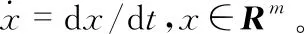
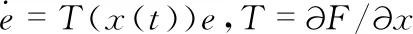
(2)
式中T为F的Jacobian矩阵。方程(2)可以表示为
e(t)=U(t,e(0))
(3)
其中,U:e(0)→e(t)线性算子映射。这个映射U的渐进行可以用指数表示为
(4)
所以,式(1)的Lyapunov指数为上述过程的平均数
(5)
通过Jacobian法计算得出的Lyapunov指数最终再代入退化过程数据得出最大预测尺度。
2 FARIMA模型
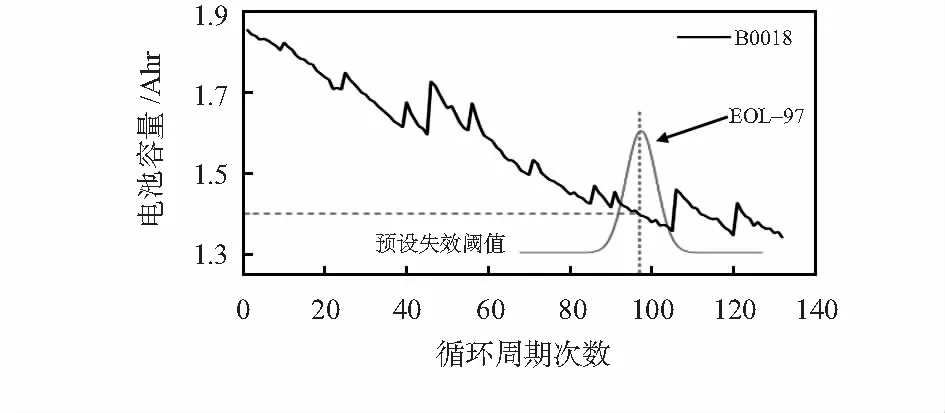
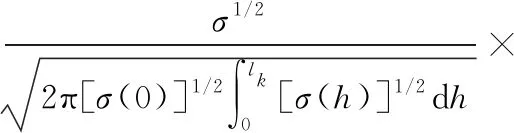
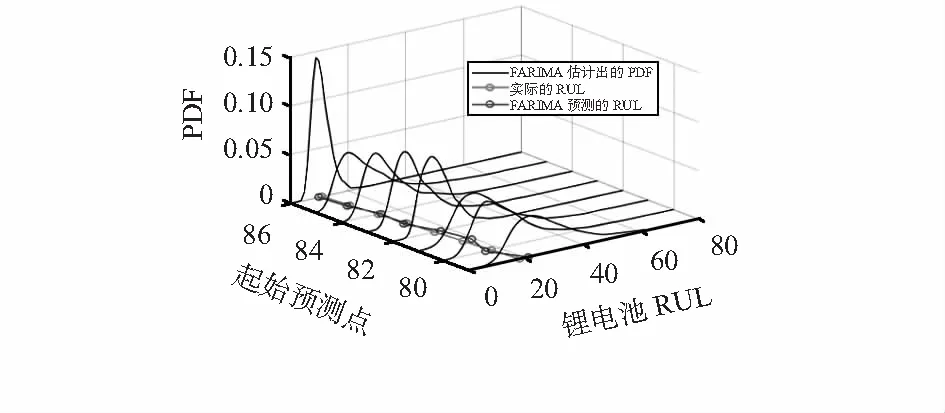
分数自回归求和滑动平均模型通常表示为FARIMA(p,q,d)。这里的参数p,q,d分别表示自回归阶数、滑动平均阶数和差分阶数。FARIMA模型同时具有长相关性与短相关性。因此,为了将FARIMA模型应用于预测,需要先对预测序列的相关性进行研究。据此给出了判断序列相关性的基本指数:Hurst指数(H)。当0 给定一个随机的时间序列{Xi},将其长度t划分为k个相邻的长度为n的子区间,其中t=kn。每个子区间的每个点与区间平均值之差的和组成一个新的序列Yi,有 (6) (7) 当n→∞时,R/S法函数曲线看起来与cnH相似,其中,c为常数,它独立于n。将上式取对数并画出对数图,其拟合曲线斜率则为Hurst估计值。 计算完Hurst指数,给出FARIMA模型定义为:如果{Xt}为平稳时间序列且满足差分方程 Φ(B)ΔdXt=θ(B)at (8) 式中 {at}为白噪声序列,Φ(B)为自回归项的p阶多项式,B为满足等式BXt=Xt-1的后移算子,θ(B)为滑动平均项的q阶多项式。Φ(B)和θ(B)的具体表达式为 Φ(B)=1-Φ1(B)-Φ2(B)2-…-Φp(B)p (9) θ(B)=1-θ1(B)-θ2(B)2-…-θq(B)q (10) 由于|B|≤1,Φ(B)和θ(B)都不为零。令Δ=(1-B)为差分算子,进而Δd表示分数差分算子为 (11) (12) 式中Γ为伽马函数。而这里的参数d与Hurst指数之间有这样的关系:d=H-0.5。因此,可以通过计算Hurst指数从而建立起FARIMA预测模型。 为了进行锂电池剩余寿命的预测估计,通常将寿命定义为退化过程第一次超过故障阈值,而这个阈值根据国际标准一般设定为锂电池剩余容量的80 %左右。这里将第一次超过这个阈值的时间点设为寿命终结点(end of life,EOL),如图1所示的来自NASA’s Ames Research Center预测数据库的锂电池开源数据集中的B0018组锂电池数据,根据所设置的阈值,B0018的EOL=97。 图1 B0018组锂电池退化过程 根据上面所测量出的EOL,退化系统的寿命T可以形式上定义为 T=inf{t∶X(t)≥ω|X(0)<ω} (13) 这里T的概率密度函数(probability density function,PDF)可以描述为fT(t)(如图1中所示的概率密度分布图),ω则为根据不同退化模型所须性能决定的预设恒定故障阈值水平。 Lk=inf{lk>0∶X(lk+tk)≥ω} (14) 同理,它的PDF为fLk(lk)。 对于阈值为ω的退化模型与之相匹配的PDF为 (15) 基于fLk(lk)的定义式可以看出,其由退化过程的漂移系数μ和扩散系数σ,及故障阈值ω和系统状态共同决定。 将利用B0018组的锂电池数据案例,以证明所提出的锂电池RUL预测模型。利用Jacobian法计算锂电池的Lyapunov指数,得到最大预测尺度为10。将电池退化数据代入计算其Hurst指数的值判断其相关性。本文采用R/S分析法来计算B0018组锂电池的Hurst指数值,最终的结果H=0.564 9。 根据已经建立好的FARIMA模型,可以对具体的锂电池退化数据进行RUL预测分析。根据上面的计算的最大尺度选择从B0018锂电池组中选择8个起始预测观察点进行RUL预测实验,并且每个起始预测时间点的时间间隔都为1个循环周期。图2为8个预测时间点分别预测出的RUL的PDF分布图。 图2 B0018组锂电池RUL预测结果 对于B0018组锂电池RUL预测最终结果,提出通过计算实际的RUL与预测得出的RUL之间的绝对误差(absolute error,AE)与相对误差(relative error,RE)来对上述预测结果进行数值分析。其计算公式为 (16) 表1 B0018组锂电池RUL预测结果及误差分析 本文介绍了一种结合混沌理论的FARIMA模型的预测锂电池的RUL的方法。根据混沌理论计算锂电池的Lyapunov指数给出其剩余寿命的最大可预测时间尺度。介绍了具有长相关性的FARIMA模型的基本形式及其原理,同时给出了判断长相关性的Hurst指数拟合方法。然后详细介绍对于锂电池退化数据的RUL的预测过程,并将建立好的模型代入进行预测。通过实际的电池退化数据利用FARIMA模型的RUL预测实验,结合实验预测效果仿真图以及误差评估指标计算的数据,证明本文提出的结合混沌理论的FARIMA模型在预测锂电池RUL时的优越性。


3 RUL预测过程
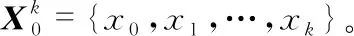
4 实验与数据分析
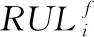

5 结 论

