基于JRNB的网络入侵检测算法*

侯占伟, 李建鹏, 王 辉

(河南理工大学 计算机科学与技术学院,河南 焦作 454000)

0 引 言

目前，在大数据环境下基于数据挖掘的算法在入侵检测中的应用逐渐成为研究的热点[1]。其中常用的算法有决策树算法C4.5[2]、极限学习机(extreme learning machine,ELM)[3]、人工神经网络(artificial neural network,ANN)[4]、朴素贝叶斯(naïve Bayesian,NB)[5]、支持向量机(support vector machine,SVM)[6]等。NB分类模型以贝叶斯定理为基础，并假设特征条件独立，即用于分类的各个特征在类别确定的情况下都是条件独立的。这一假设使得NB分类模型具有容易实现、训练学习时间较短、预测效率稳定的特点，但同时该假设也带来了局限性[6]，它使属性间的依赖关系无法体现，这与互联网中数据具有的复杂关系并不相符，因而在一定程度上牺牲了分类的准确率，表现出对网络行为预测能力较差的缺点。因此众多学者针对这一算法缺陷对其进行各种方式的改进，以改善分类效果。

Chen Z G等人[7]提出利用决策树扩展NB的入侵检测算法，并结合特征简化技术来获得极大后验概率，提高了分类的准确率。但该算法在校验数据的过程中会产生大量伪数据，具有对分类产生干扰的缺点。Koc L等人[8]在入侵检测中利用隐朴素贝叶斯(hidden naive Bayesian,HNB)算法，在NB的基础之上对每一个属性节点添加一个隐藏的父节点，以此来体现属性间的关联关系，减少属性间独立性假设带来的影响，进而提高了分类精度。但在关系网络具有多重属性时，此算法的分类效率表现较低。董立岩等人[9]提出一种半监督式学习的NB(semi-supervised naive Bayesian,SNB)算法，该算法通过利用置信度来选取取无标签训练集中的子集，再结合带标签的样本，不断迭代直至完成训练。实验结果显示，相较于传统NB算法预测准确率得到了明显提高，但算法在数据量较小时仍然需得到置信度列表，增加了算法的耗时。王双成等人[10]提出了一种动态完全NB分类算法，利用多元高斯核函数来计算属性的条件联合密度，并使用平滑参数优化方法，有效地结合了属性间的依赖关系，但在大数据环境下，算法的效率有所降低。

本文在前人的研究基础之上，提出一种利用JS散度和反类别频率(reverse class frequency,RCF)改进NB算法，即JRNB算法的入侵检测方法。方法在传统NB算法中引入权重因子来计算每个特征权值，权重因子通过JS散度和RCF计算获得，使得检测率和检测精度都有了提高，误检率也相应降低。

1 JRNB分类模型

1.1 NB分类器

给定一个训练样本集U={X1，X2，…,Xn}，其中,元素Xi={a1，a2，…,am|ai∈Ai}表示每条数据记录，ai表示这条数据记录的第i个特征，Ai表示样本集的第i个属性变量，可以是离散值或是连续值。设有类别集合C={c1，c2，…,ck|k≤n}，映射函数f∶Xi→ci表示将任意一条数据记录归类为集合C中的一个类别标签ci。现考虑一个待分类的测试样本集T={Y1，Y2，…,Yr}，计算测试实例Yi属于类别cj(∀j=1,2,…，k)的概率情况，得到计算结果集P={p1，p2，…,pk}，进一步得到集合P中的最大元素pt，最终将测试实例归类为ct。计算步骤如下：

1) 计算样本集U中类别c出现的概率

(1)

式中ci为样本Xi所属类别，n为U中元素的个数。

2)计算集合U中样本类别为c的情况下特征aj出现的条件概率，若属性Aj为离散值

(2)

式中aij为训练样本实例Xi的第j个特征。若属性Aj为连续值，有

(3)

3)计算样本集U中特征aj出现的概率

(4)

4)计算Y′属于类别ci的概率

(5)

式中Y′为待测样本实例，m为样本属性的个数。

5)由式(5)可以计算出待测样本Y′属于∀ci(1≤i≤k)的概率，得P={p1，p2，…,pk}，对k个概率值进行归一化，排序可得样本Y′属于每个类别的相似度，得出最大后验概率MP

(6)

6)由上述结果可给出NB分类器的定义

Classifier(T={Y1,Y2,…,Yr})=

(7)

1.2 特征加权

本文使用一种特征加权算法，依情况赋予不同特征项对应的权值，以提高分类准确率。

定义1 称weight(i,j)为类别ci中特征aj的权值，即衡量特征aj在分类过程中对类别ci的重要程度。

以此对NB公式进行改进

(8)

1)KL散度

欲进一步量化特征aj对类别ci的重要程度，可以考虑ci在样本集中的概率分布与在具有特征aj的样本集中的概率分布两者之间的差别。差别越大，则特征aj对类别ci越重要;反之，则对类别ci的代表性越差。根据文献[11],可以利用KL散度(Kullback-Leibler divergence)描述两种概率分布之间差异，再利用计算出来的差值来表示特征在分类过程中的重要程度，计算公式如下

(9)

2)JS散度

由KL散度计算式(9)可以看到其局限性，其用来表示两个概率分布之间的距离差，但不具有对称性，因此,不能算作是真正意义上的度量;其次，其结果范围也没有界限。本文通过引入JS散度(Jensen-Shannon divergence)的方法来对其进行改进，以弥补上述的不足。文献[12]已给出结论，JS散度具有对称性，是真正意义上的距离度量。另外它的取值范围在0～1之间，用来进行相似度的判断更加确切方便。因此,可以将JS散度引入到NB分类算法当中，并利用它比较两种概率情况的距离差来赋予特征项相应的权值，计算公式如下

(10)

定义2称WJS(i,j)为类别ci中特征aj的JS权重因子。

将式(9)代入式(10)可以得出WJS(i,j)的计算方法。由式(11)可以看出，特征aj在样本集中的分布越分散，则对于类别ci的JS权重因子越小，若特征分布较为集中于类别ci，则JS权重因子越大

(11)

3)反类别频率

引入JS散度的特征加权方法,注重的是类别内具有特征项的样本在不同类别间的比例上，体现的是类别间的聚集程度，而没有考虑类频率对样本分类的影响。文献[13]证明，含有特征项的类别数与总的类别数之间的比例也是对特征项重要程度的一条判断依据。由于对特定类别具有代表性的特征项出现于少数类中，因此，可利用RCF来对其做进一步改进。

定义3称WRCF(j)为特征aj的RCF权重因子。计算公式如下

(12)

式中NC为总类别数。

1.3 算法描述

通过结合上述权重因子WJS和WRCF来计算特征权值weight

weight(i,j)=WJS(i,j)×WRCF(j)

(13)

基于PCA构造属性集及上述特征加权方法，本文提出JRNB分类算法，具体实现如下：

算法1JRNB算法

Input：训练样本集U，待分类样本实例Y={a1,a2,…,am}，类别标签C={c1,c2,…,ck}

Output：样本Y所属类别cY

1)k=类别数量

2)∥获得先验概率P(ci)

3) for eachiink

4)n=0

5)s=0

6) for eachXinU

7)n=n+1

8) if(X∈ci)

9)s=s+1

10) end for

11)P(ci)=s/n

12)end for

13)∥记录样本Y属于各个类别的概率

14)P={p1,p2,…,pk}

15) for eachiink

16)P(Y|ci)=1

德国建立了与市场经济相适应的城市垃圾处理管理体系，形成了良性循环的发展机制。政府对行政管辖区范围内及运至服务区范围内的垃圾进行合理的规划和管理，制定合理的实施计划，强化监管，鼓励先进的、有利于垃圾减量和资源回收利用技术的应用和发展。市场机制贯穿于垃圾收运处理的全过程，公私合营的PPP模式运转良好。尽管不同城市有不同的运行机制，但都以垃圾收费作为基础，选择合格的私人企业服务商代替政府经营，私人企业服务商的服务需要满足公众、机构、工业和商业等的综合要求。政府购买服务模式，既提高了效率，又保证了服务质量，体现出垃圾处理的公益性。

17) for eachjinm

18)weight(i,j)=WJS(i,j)*WRCF(j)

19)P(Y|ci)=P(Y|ci)*P(aj|ci)*weight(i,j)

20) end for

21)pi=P(ci)*P(Y|ci)

22)end for

23)cY=(ci|pi=max{p1,p2,…,pk})

1.4 JRNB入侵检测模型

将JRNB算法用于入侵检测模型之中，通过对相应的网络流量数据进行一系列过程处理，最后，获得网络事件的分类结果。入侵检测模型流程如图1所示。

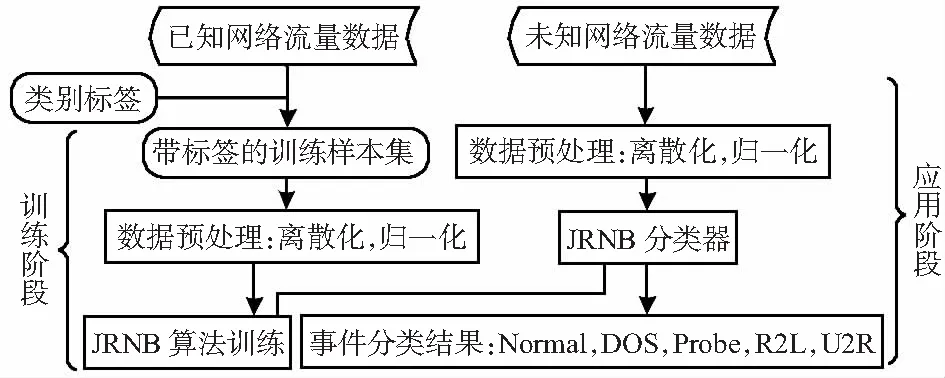
图1 基于JRNB算法的入侵检测模型

2 仿真实验结果与分析

仿真实验所搭建的环境平台使用的操作系统为Windows 7，CPU频率为2.4 GHz，内存为4 G，硬盘存储空间为500 G，编程语言采用Python 3.6。入侵检测数据集采用NSL-KDD，它是对KDD 99的改进，解决了KDD99中存在的固有问题，作为当前入侵检测领域的标准数据集，已被广泛使用。该数据集有41个特征，攻击类型分为4大类。对于实验中各种方法性能的对比，采用下列指标进行评估

(14)

(15)

(16)

在入侵检测中，漏报带来的危害往往比误报更大，因此，对检测率的要求更受到人们重视。由表1看出，JRNB算法相较于NB算法不仅检测率有了明显的提升，同时也保证了较高的检测精度与较低的误检率。由此说明，引入JS散度和RCF特征加权方法改进NB的方法是可行的。

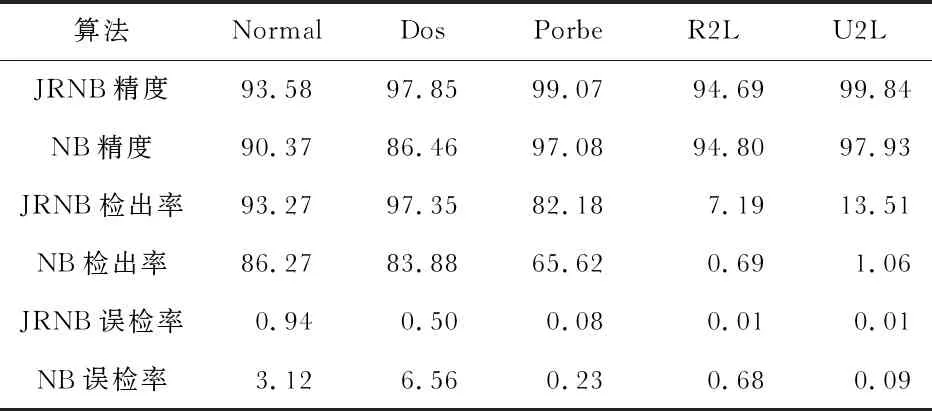
表1 算法改进前后检测性能对比 %

将JRNB算法与其他分类算法(SVM，C4.5)及改进的NB(HNB，SNB)算法在入侵检测方面做比较，并利用检测精度、检出率和误检率对结果进行衡量。由图2(a)看出，新算法对Normal，Dos，R2L的检测精度有较为明显的提高；从图2(b)中看出，在检测率方面，除了对Dos的检测率稍低于SNB方法外，对其他各种入侵类型的检测率都有了一定的提升；图2(c)说明，除了Probe和U2R以外，新算法相较于其他各入侵类型的误检率都有了显著的降低。由以上各类实验结果说明了JRNB算法能够在保证检测精度及检测率提高的同时，对误检率也有所降低，以满足实际需求。

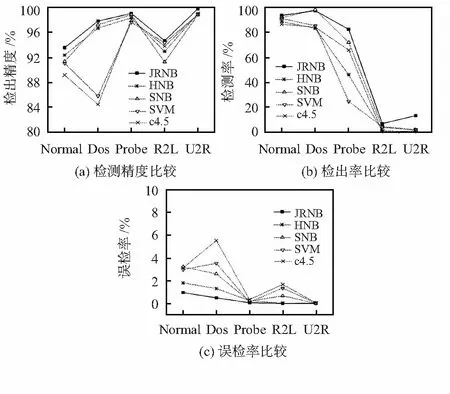
图2 各分类算法性能比较

3 结束语

本文使用了NB相关理论知识，并提出改进的JRNB算法。通过JS散度和RCF为每个特征项引入权重因子来减小NB的条件独立性假设的局限性。通过仿真实验表明:本文提出的基于JRNB的网络入侵检测算法相比于传统NB算法及其他流行分类算法在检测性能上有了一定的改善。下一步工作研究如何更有效地对数据进行预处理的方法，以提高JRNB算法的稳定性及适应性。