基于图像形态学运算的周期错位校正方法研究*

张啟航， 张秋菊， 贾君慧， 荆泽成

(1.江南大学 机械工程学院，江苏 无锡 214000;2.华中科技大学无锡研究院 机器人中心，江苏 无锡 214000)

0 引 言

作为人工智能的重要元素,机器视觉已经被广泛地应用在工业机器人、目标识别、视觉检测与三维(3D)测量等领域，并不断地推进产业智能化的转型[1]。结构光三维测量因为其具有处理速度快、硬件成本低和测量结果精度高等优点，在机器视觉三维非接触测量领域具有广阔的应用前景[2～4]。结构光三维测量是通过投射设备向待测物体投射预先编码好的图像，并由一个或多个相机进行图像的采集。基于相机采集的图像进行解码操作，进而对匹配点进行三角测量法计算，求解出目标物体表面采样点三维坐标。该方法在缩短测量时间，提高测量效率方面优势尤为突出[5]。

目前基于结构光编码与解码的方法研究有很多，其中,格雷编码因其相邻两个值最多只存在一位误码以及抗干扰能力强等优点，在结构光应用中最为广泛[6]。Zheng D L等人[7]提出了一种使用自适应中值滤波器的方法，有效地消除了图像噪声所产生的格雷码解码误差。黄治凡等人[8]介绍了一种基于双目单视面和结构光的三维复原方法。雷震[9]提出了一种直接格雷码编码的结构光测量方法，但提高了视觉系统搭建的难度。崔海华等人[10]采用了一种基于格雷码—相移的组合光编码技术对目标物体进行三维测量，实现了相机视场的无极细分，提高了编码的分辨率与稳定性,但未考虑周期错位现象可能带来的误差影响。尹丽萍等人[11]在研究茶壶的三维测量过程中，引入了格雷码和相移结合的编码方式，分析了解码过程中存在的格雷码和相移结果周期错位的问题，提出了一种以相移周期为基准的格雷码周期调节方法，该方法有效地规避了物体表面出现不连续或者陡峭的解码误差。林焕等人[12]针对格雷码—相移解码过程中存在的周期错位问题，提出了一种新的校正方法，并对人眼石膏模型进行三维测量；该方法基于相移解码结果对格雷码解码过程添加三个约束条件，进而对目标点的主相位值进行插值求解。文献[11]和文献[12]均对三维测量中周期错位现象进行校正，但其方法的处理精度受图像噪声和外界光环境影响较大，当采集的图像中被测物体边缘处有较多的图像噪声时，此方法处理结果无法取得一个很好的周期错位校正结果。

本文基于格雷码—相移组合结构光解码过程中出现周期错位现象的原理，分析了单个周期内所有可能出现的周期错位现象，并提出了一种新的基于图像形态学运算原理的周期错位校正方法，该方法能有效地消除组合结构光解码过程中绝对相位的求解误差。最后通过搭建双目结构光测量系统，完成对三维实体模型的点云重构实验，对比分析未校正的结果和校正后的结果，验证了该方法的有效性和可靠性。

1 格雷码与相移结合的解码原理

1.1 格雷码解码原理

在格雷码解码过程中，首先需要对图像进行二值处理，实现格雷码模式的二值化，再将每个像素点对应的格雷码数值转化为二进制数值，最终再转换为与之对应的十进制数值，此时的十进制数值就是该像素点所对应的格雷码数值即该像素点所在的周期数[13]。

1.2 相移解码原理

为了在格雷码解码结果的基础上对像素点周期进行进一步的细分，需要对投影仪投射的四副相移图像进行解码操作，求出对应像素点的相对相位[14]。投影仪投射的四幅相移图像中第i幅相移图像中每一个像素对应的光强为

Ii(x,y)=130+100×cos[2×π×(x+21)+0.5×i×π]

(1)

式中Ii(x,y)为该像素点对应的光强，i为对应的相移图像编号(1≤i≤4)，(x,y)对应像素点坐标。

求取相对相位时，将四幅相移图像对应的各个像素点光强I1，I2，I3，I4分别代入到式(2)中，根据相移图像光强变化规律以及反正切函数性质可知，相对相位φ(x,y)在(0，2π)之间周期线性变化

(2)

式中φ(x,y)为该像素点对应的相对相位。

为了获得目标图像连续单值的测量空间划分，必须保证格雷码解码周期与相移解码周期完全吻合，格雷码和相移解码效果如图1所示。

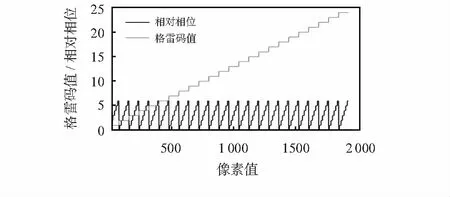
图1 格雷码—相移解码结果

1.3 绝对相位求解原理

在双目结构光三维测量系统中，双目相机的像素点匹配精度取决于绝对相位求取的准确性。分别将求解出的格雷码值和对应的相对相位值分别代入式(3)中求解绝对相位[15]

φ(x,y)=2×π×Z(x,y)+φ(x,y)

(3)

式中φ(x,y)为该像素点的绝对相位，Z(x,y)为像素点对应的格雷码值，φ(x,y)为像素点对应的相对相位。

2 周期错位调整

2.1 周期错位现象

在实际测量过程中，由于环境光照强度不同、图像噪声、光栅投影精度以及格雷码解码与相移解码结果误差等影响，可能会导致格雷码突变周期与相移周期产生错位现象，从而导致绝对相位的平滑曲线中出现突变三角形，实际绝对相位图像如图2(a)所示。例如在相移解码结果中,φ(x,y)=2π，与其相邻的像素点相对相位φ(x+1,y)=0，此时相对相位产生突变，从2π突变到0，而与之对应的实际格雷码值未满足Z(x+1,y)=Z(x,y)+1的突变条件，因此,在绝对相位的结果中，φ(x+1,y)处会产生一个向下的突变，实际效果如图2(a)中明显的灰白色条纹部分，此时绝对相位曲线中出现凹错位台阶现象(如图2(b)中向下突起的部分)，进而无法达到对目标图像进行连续单值的测量空间划分的目的，称此现象为周期错位，周期错位能否得到有效的校正是格雷码—相移结构光解码技术的关键。

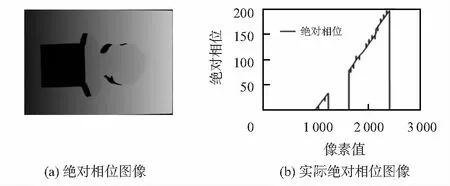
图2 实际绝对相位结果

2.2 周期错位分析

本文采用以相移周期为准，对格雷码周期进行校正，在校正之前，需对可能出现的周期错位情况进行分析。取一完整的相移周期如图3中相移参考标准周期所示，此时，在当前周期内，格雷码解码结果应如图3中正确格雷码周期部分所示，格雷码周期应与相移周期保持完全一致。在实际解码过程中，所有可能出现的周期错位现象如图3中错位格雷码周期部分所示，共有6种情况，故周期错位校正方法必须保证图示6种情况得到正确的校正。

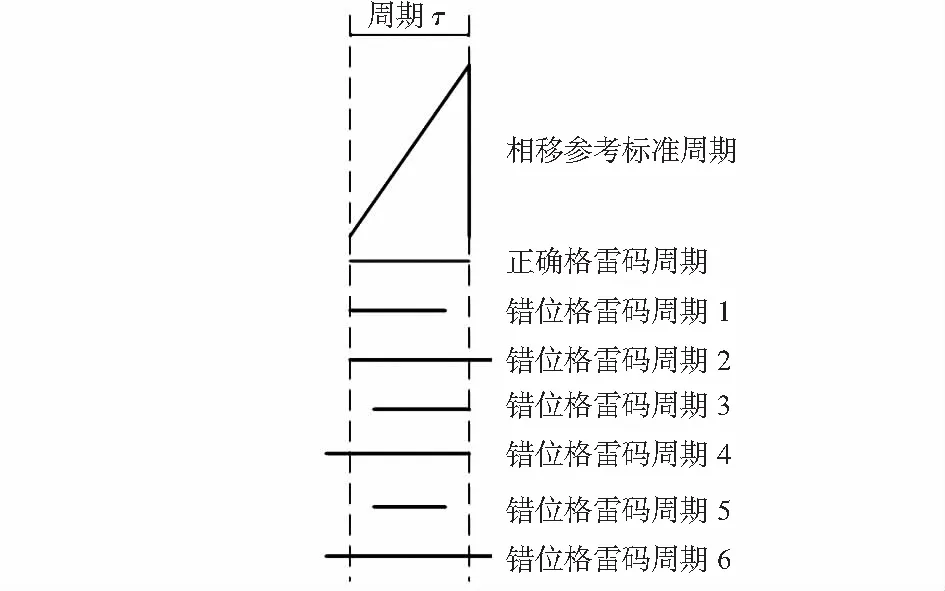
图3 周期错位分析

2.3 周期错位调整

针对上述的周期错位问题，本文提出了一种新的基于图像形态学运算原理的周期错位校正方法。以相对相位的突变周期为准校正格雷码数值，对格雷码解码结果进行膨胀、腐蚀和卷积等图像形态学运算操作，保证其周期与相移突变周期保持严格一致，从而解决格雷码—相移解码周期错位问题。

为了直观地观察周期错位校正效果，以左相机采集的图像中第1 000行像素点处理过程为例，取相移解码图像中每个周期内像素点灰度值中值为阈值，对相移解码结果进行二值化处理，生成两幅二值图像。

提取出格雷码解码图像中灰度值为第一周期对应值的所有像素点，将其余像素点的灰度值均改为0。此时，其图像灰度值结果如图4(a)所示。对图4(a)对应的图像进行膨胀操作，将预先测试好的核和对应图像代入式(4)中进行卷积。膨胀后图像分别与相移二值化图像进行卷积，完成对上述周期错位现象1、现象3和现象5对应周期内缺失的部分第一次填充处理。卷积后的结果如图4(b)所示。式(4)如下

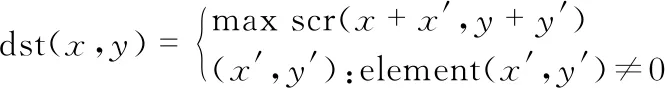
(4)

式中 dst(x,y)为膨胀后图像，element(x′，y′)为与处理图像卷积计算的核，scr(x，y)为处理前的图像。

基于膨胀后的图像进行腐蚀操作，将对应的核和膨胀后图像分别代入式(5)中进行卷积，得到对应的腐蚀后图像结果，完成对上述周期错位现象2、现象4和现象6对应周期外的部分进行有效的处理。腐蚀后进行第二次膨胀处理，将腐蚀结果代入上式(4)中，获得第二次膨胀后图像如图4(c)，此时得到的图像再分别与相移二值化图像进行卷积，卷积后的图像相加，进而保证所有周期错位现象均可得到校正，得到第一周期内格雷码校正后结果，如图4(d)所示。式(5)如下

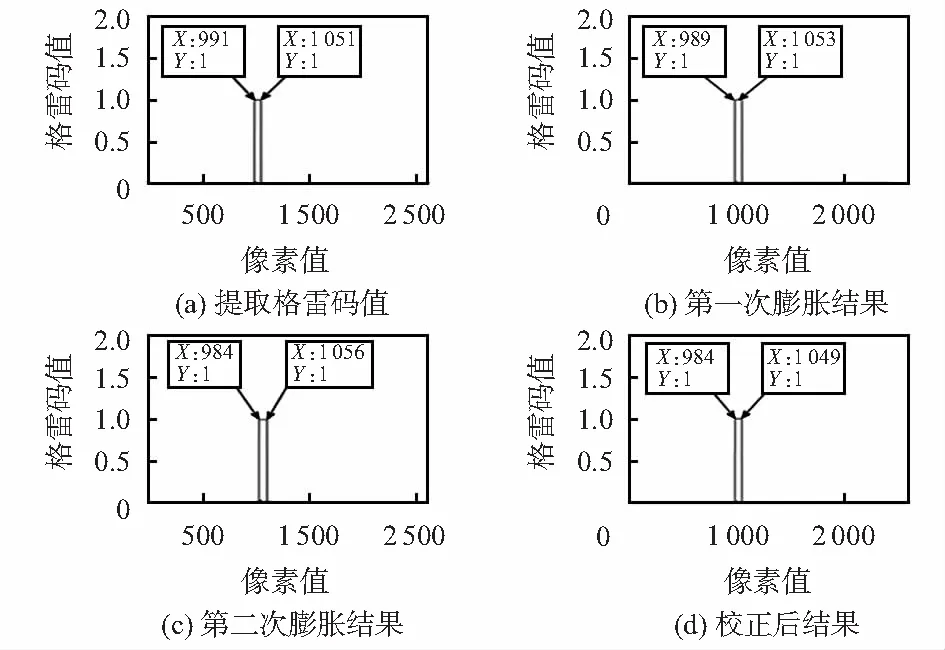
图4 第一周期格雷码校正过程

(5)

式中 dst(x,y)为腐蚀处理后图像，element(x′，y′)为与处理图像卷积计算的核，scr(x，y)为处理前的图像。

重复以上操作，完成格雷码所有周期的校正操作，校正后的格雷码值周期与相移周期保持完全一致，如图5所示，此方法有效地消除了周期错位现象。

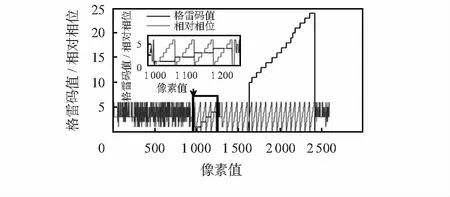
图5 周期校正后格雷码结果与相移解码结果

3 实验结果与分析

实际搭建了格雷码—相移结合的光栅结构光双目视觉系统，如图6所示，该系统由工业相机、投影仪、计算机、标定板和石膏娃娃组成。

图6 结构光双目视觉系统

首先由两个工业相机对标定板进行图像采集，计算机处理采集的图像完成对相机的标定。然后再通过计算机控制投影仪依次向石膏娃娃投射预先编译好的格雷码—相移图像，并控制两个工业相机实时进行图像采集，运用上述解码方法分别对左右两个相机采集的所有图像进行格雷码解码和相移解码操作，再以相移解码结果为基准按照上述周期错位校正方法对格雷码解码结果进行周期错位校准，消除左右图像中像素点匹配的周期错位误差，求取图像中各像素点的绝对相位。最后基于绝对相位的结果进行左右两个相机各个像素点的匹配，将左右两幅图像中像素点绝对相位相等或最接近的点进行匹配，完成对石膏娃娃的点云重构操作。

通过上述流程完成对格雷码和相移编码的解码工作，并按照本文提出的方法进行周期错位校正。在MATLAB软件中提取处理结果中的第1 000行像素点，以每一个像素点所对应的绝对相位值生成曲线，将未进行周期校正的实验结果、按照文献[11]和文献[12]提出的周期错位校正方法校正后的实验结果以及按照本文提出的方法处理后的结果进行对比分析，如图7所示，通过曲线可明显比较出周期错位校正效果。

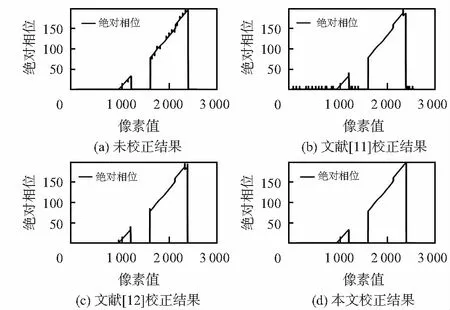
图7 程序处理结果

未进行错位校正的结果中，目标物体上绝对相位中有很多突变位置，此现象会导致像素点匹配过程中产生误差。按照文献[11]中的周期错位校正方法能消除目标物体上大多数的周期错位现象，但此方法受图像噪声和环境光照影响较大，从图7(b)上可以看出，该方法在降低周期错位误差的同时在目标物体外界背景中产生了新的错位现象，虽不影响目标物体的点云匹配，但在点云重构结果中，目标物体外界会产生少量的噪点。按照文献[12]的校正方法在降低图像噪声影响的方面较文献[11]有较大改善，但仍会在物体边缘处会出现误判的情况，其校正后效果如图7(c)所示。从图7(d)上可以明显看出，按照本文提出的方法对解码结果进行周期错位校正，可以有效地消除周期错位现象且并不会受环境光等外界因素影响，保证了解码结果的准确性，提高了后续像素点匹配精度，验证了本文提出的周期错位校正方法的有效性和稳定性。

基于正确的像素点绝对相位结果，完成双目相机像素点匹配步骤从而达到对实际石膏娃娃点云重构的目的，三维重构结果如图8所示。

图8 石膏娃娃点云重构

4 结束语

本文基于格雷码—相移组合结构光解码过程中出现周期错位现象的原理，分析了单个周期内所有可能出现的周期错位现象，提出了一种新的基于图像形态学运算原理的周期错位校正方法，并对三维实体模型进行三维重构实验，对比未周期校正的结果、按照文献[11]和文献[12]方法校正的结果和按照本文的方法校正后的结果，体现出本文周期错位校正方法在消除周期错位误差和规避外界光环境影响方面的显著优势，验证了本文校正方法的有效性和可靠性。