白垩系冻结砂岩动态统计损伤本构关系研究

秦 越，王 磊，苏宏明，陈世官

(西安科技大学建筑与土木工程学院，西安 710054)

我国西部地区煤矿多为侏罗系煤层，其上覆巨厚白垩系基岩，矿井建设中为了降低地下水对井壁质量和施工作业环境的影响，冻结法成为白垩系弱胶结软岩地层立井施工最佳方案。在井筒开挖掘砌过程中，立井周边冻结围岩由于承受来自爆破与机械凿岩等动载作用，会产生不同程度的损伤。因此非常有必要对该类岩石在冲击载荷作用下动力学特性展开研究，并对其本构关系进行表征，为相关工程开展提供理论依据。

岩石本构理论的发展对实际工程开展的指导义重大，国内外学者对此类岩石动、静态本构关系的研究取得了一系列有价值的成果。在静态本构关系研究方面，田斌等[1]通过偏应力与孔隙坍塌理论对高孔隙砂岩破坏机理进行分析，建立了描述高孔隙砂岩流体饱和时力学特性的盖帽型本构模型。刘建等[2]通过改进的Duncan模型描述砂岩在不同水溶液作用下的水物理化学作用效应。朱杰兵等[3]在分析砂岩三轴卸荷流变试验结果的基础上，提出考虑损伤的Burgers流变模型，能较好描述卸荷条件下砂岩的衰减蠕变阶段和稳定流变特性。姜立春等[4]对酸性溶液蚀化下砂岩开展单轴压缩试验，依据Weibull函数与Lemaitre应变等效原理建立了损伤本构模型。邓华锋等[5]对经历水岩作用的砂岩开展三轴压缩试验，根据应力-应变曲线、连续损伤力学与统计理论，建立考虑损伤效应的损伤统计本构模型。郑广辉等[6]根据不同饱和度砂岩静态压缩试验数据，在宏观唯象损伤力学与Lemairte损伤模型的基础上拟合得到分段式水软化-应变损伤本构关系。单仁亮等[7]建立的三维蠕变模型可准确反映处于三轴压缩状态的冻结层状红砂岩的轴向与径向蠕变全过程。魏尧等[8]对白垩系饱和冻结砂岩开展不同围压的三轴蠕变试验，基于现有黏弹塑性模型提出考虑温度及损伤效应的蠕变本构模型。在动态本构关系研究方面，赵光明等[9]考虑软岩的应变硬化与塑形流动等动力学特性，将现有朱-王-唐模型中的非弹性弹簧用损伤体替代，构建了能较好描述软岩材料动力学特性的黏弹性动态统计损伤模型。蔡灿等[10]在分析中低应变率冲击对岩石动力学特性影响的基础上，依据元件组合理论将Maxwell体、Bingham体及损伤体并联，提出了描述中低应变率情况下岩石动态损伤的本构模型。江雅勤等[11]根据单轴冲击试验中砂岩的应变率效应和损伤软化效应，通过元件型建模方式提出考虑损伤的砂岩本构模型。Wang Lei等[12]以现有黏弹性本构模型为基础进行改进，考虑应变率效应和温度效应，建立了非线性体(线性体)、Maxwell体和损伤体并联的黏弹性动态本构模型。

由上述研究成果可知，目前有关饱和冻结砂岩动态本构关系的研究相对较少。根据SHPB冲击试验获得冻结砂岩在不同应变率下的动态应力-应变曲线，在分析岩石动力学特性的基础上，建立基于Weibull统计分布、D-P破坏准则及等效应变原理研究冻结砂岩强度型动态统计损伤本构关系，通过线性回归法确定模型参数后，将理论曲线与实测数据进行比较，证明了模型的准确性和适用性，为西部矿区立井建设中冻结爆破凿井工程提供理论指导。

1 饱和冻结砂岩SHPB试验

1.1 SHPB装置及工作原理

动态冲击试验在西安科技大学岩石类材料动力实验室进行，所用SHPB系统结构组成如图1所示。装置主要由加载驱动系统、压杆系统、能量吸收系统、信号采集系统以及信号处理系统等组成。杆系由高强度合金钢制成，其中子弹长300 mm，入射杆长3 700 mm，透射杆长2 500 mm，弹性模量E=210 GPa，密度ρ=7 800 kg/m3，理论波速C=5 172 m/s。

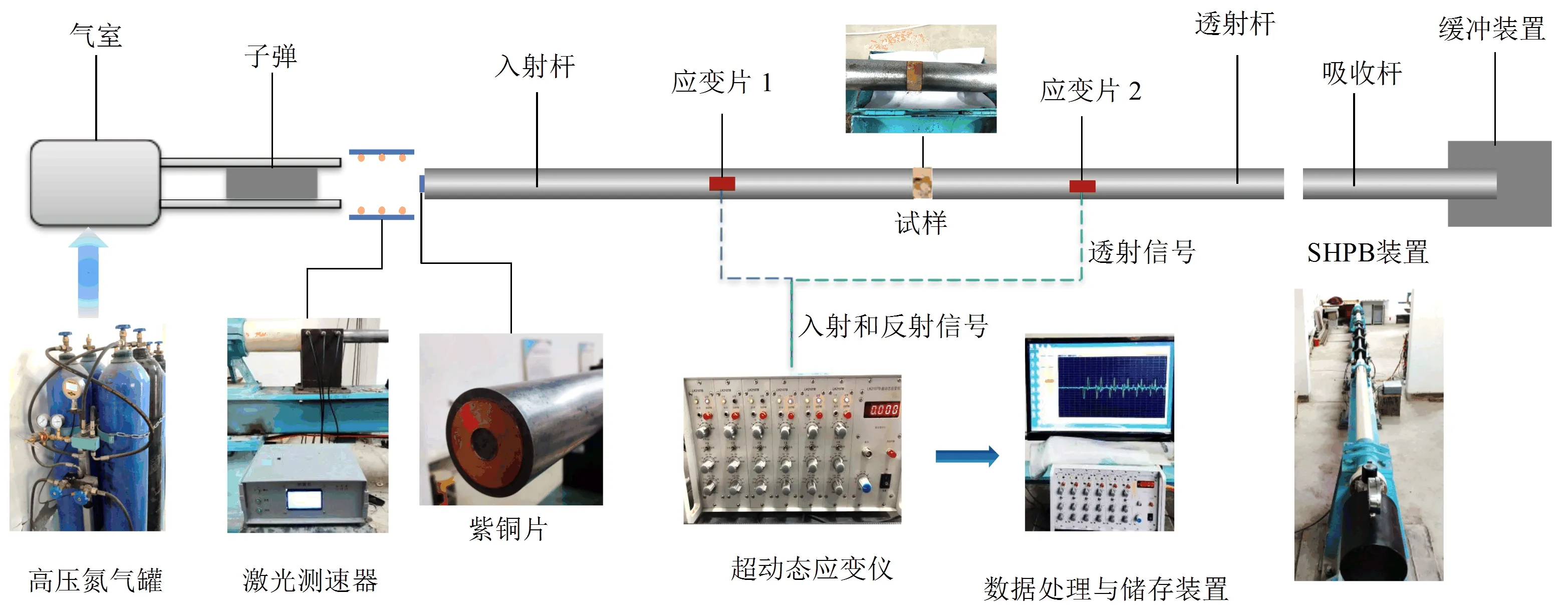
图1 SHPB系统结构Fig.1 Structure of SHPB system

弹性应力波传播理论是SHPB系统的基本工作原理，立足如下假设：①压杆中应力波为一维状态；②试样中应力均匀；③压杆应力波为平面应力波；④杆系在试验过程中为线弹性状态。采集的信号可通过三波法公式(1)计算得到试样的动态力学参数。

(1)

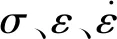
1.2 试验过程

依托甘肃省五举煤矿，选取冻结凿井过程中穿越的白垩系富水弱胶结红砂岩为研究对象，其基本物理力学参数平均值如表1所示。借助烘箱和超声波测速仪筛选出干密度与波速相近的试样后，利用真空饱和装置与低温控温箱获得-30 ℃饱和冻结砂岩试样进行试验。

表1 砂岩物理力学参数平均值Table 1 Average physical and mechanical parameters of sandstone

试验共分为5组，每组至少3个试件，对试样进行不同冲击气压的单轴冲击试验，加载应变率范围110～220 s-1。试验结果在剔除离散性较大的个别数据后取均值，动态力学参数如表2所示。

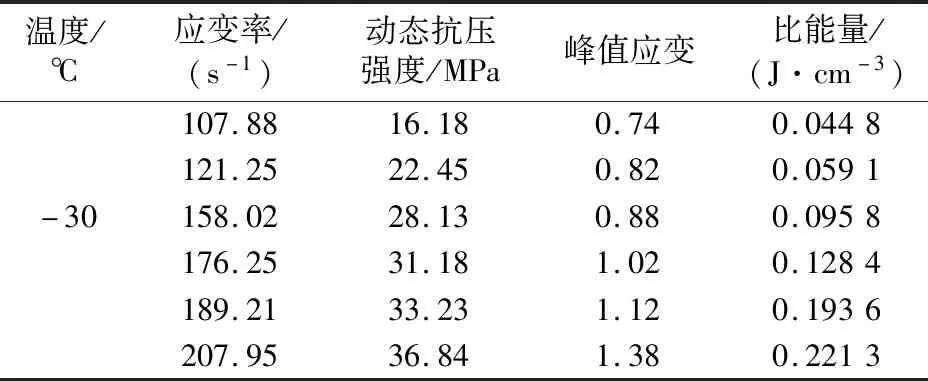
表2 饱水冻结红砂岩动态力学参数Table 2 Dynamic mechanical parameters of saturated frozen sandstone

2 动力学特性分析

2.1 强度与变形的应变率效应

-30 ℃饱和冻结砂岩在不同加载应变率下的动态应力应变曲线如图2所示。

图2 不同应变率下-30 ℃砂岩应力应变Fig.2 Stress-strain of sandstone at -30 ℃ under different strain rates

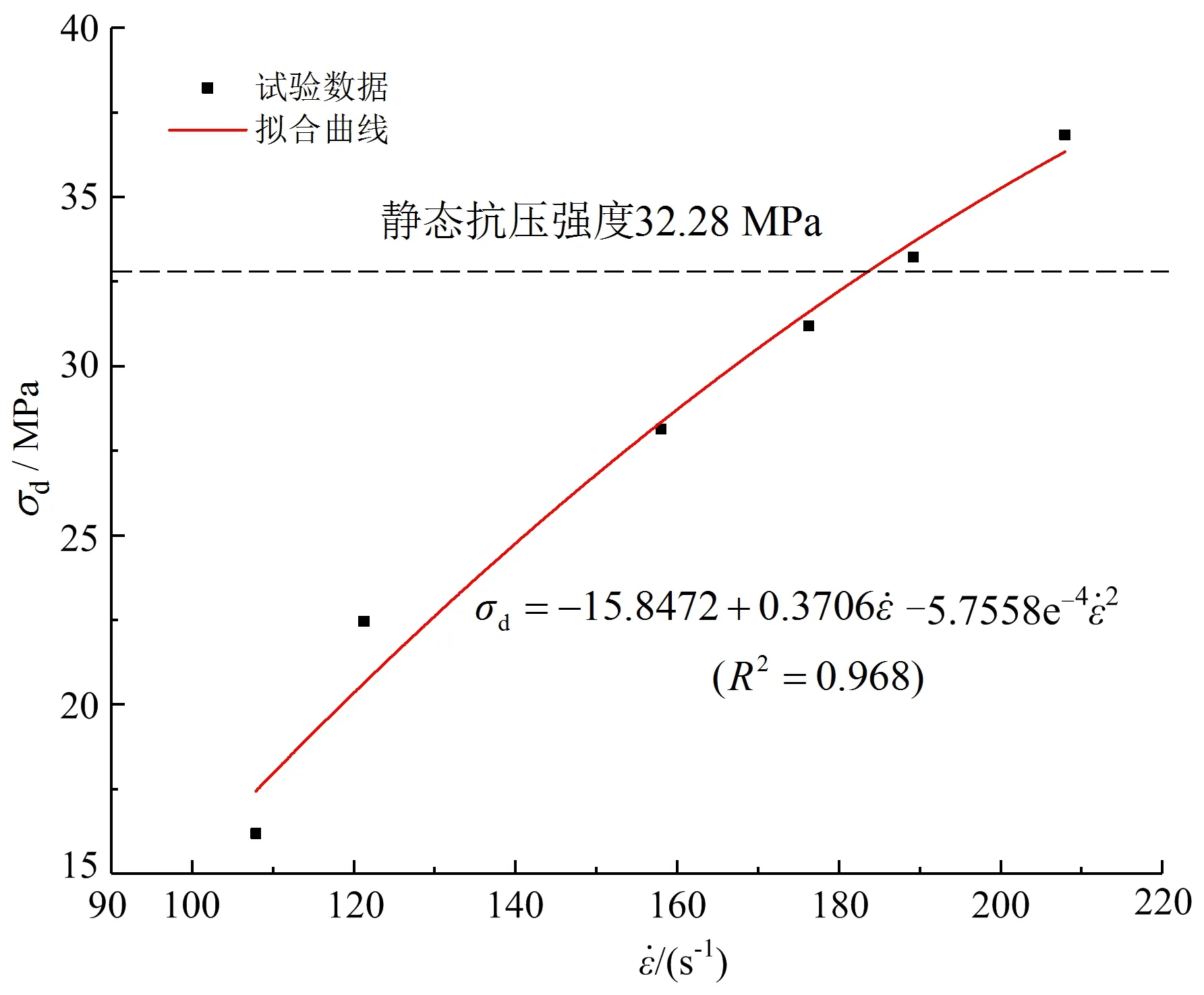
图3 动态抗压强度与应变率的关系Fig.3 Relationship between σd and

试样峰值应变与应变率关系如图4所示。由指数函数拟合曲线变化趋势可知：试样峰值应变同样具有应变率效应，且应变率越高，应变增长幅度越大，即-30 ℃时饱和冻结砂岩属于率相关性较强的材料。

图4 峰值应变与应变率的关系Fig.4 Relationship between εd and

2.2 能量吸收的应变率效应

为了反映岩石在冲击过程中的能量吸收情况，消除试样尺寸的影响，从能量角度解释应变率效应，采用比能量吸收值SEA来表征能量消耗情况，按下式(2)计算：

(2)

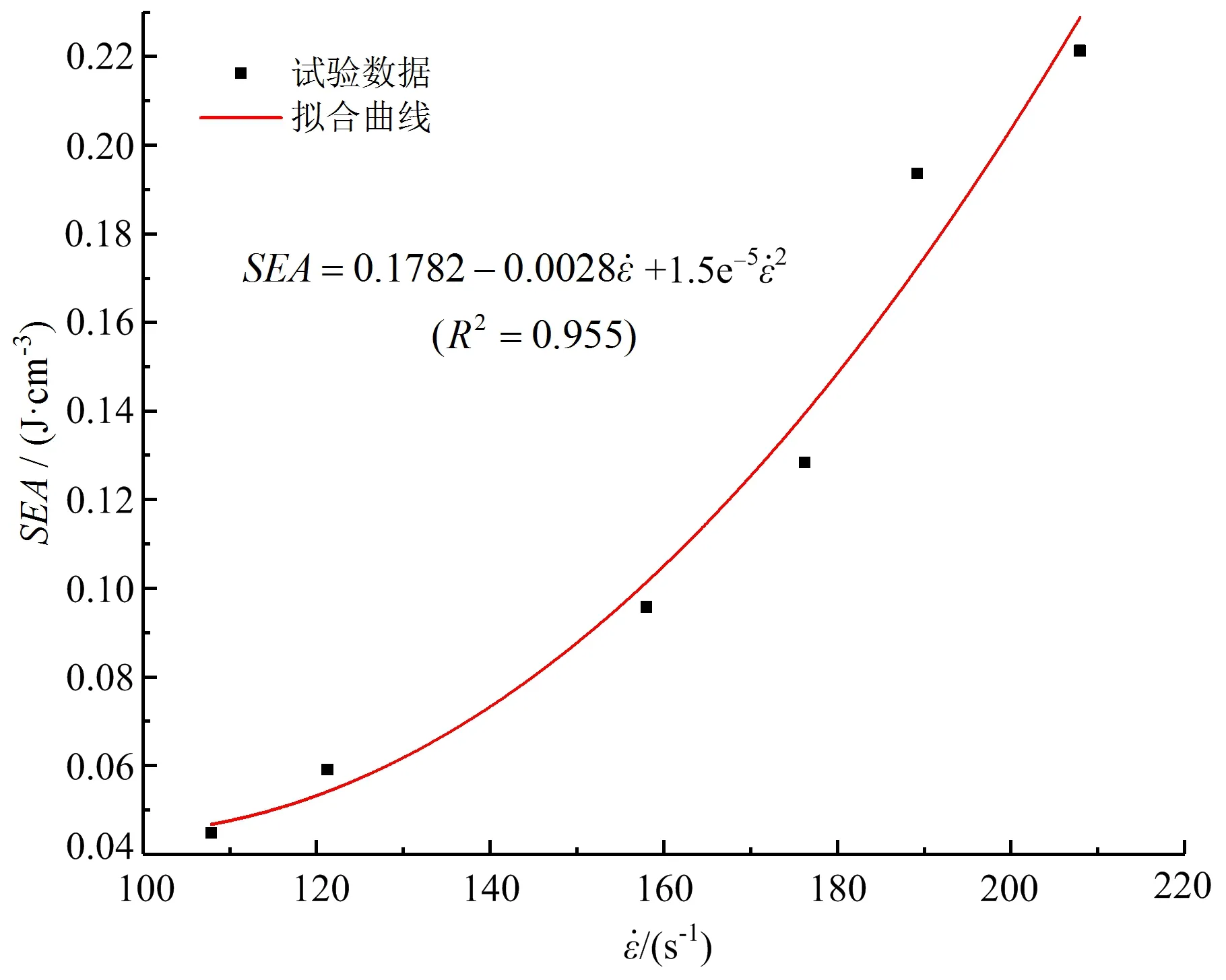
图5 比能量吸收值与应变率的关系Fig.5 Relationship between SEA and

(R2=0.955)

(3)

从能量吸收角度分析试样动力学参数的应变率效应可知：西部白垩系弱胶结砂岩内部随机分布大量孔隙、裂纹等微缺陷[12]，试件在冲击载荷下的破坏过程伴随着裂纹的产生、扩展和贯通，并且裂纹衍生所需的能量高于裂纹扩展[13]。应变率较低时，弹性杆中入射能较小，基本转化成反射能和透射能，试样吸收的能量很低，只有需要较少能量的裂纹扩展；随着应变率逐渐升高，弹性杆中的应力波会携带更多的能量作用在试样上，导致岩石内部用于裂隙衍生和扩展的能量随之变大，参与破坏过程的裂隙增多，宏观上表现出动态抗压强度、峰值应变及比能量吸收值的应变率相关性明显。

3 强度型动态统计损伤本构关系

3.1 统计损伤演化方程

岩石材料在冲击载荷下损伤来源于局部微元体的非线性渐进破坏，材料与微元体具有如下性质：

①砂岩属于各向异性的损伤体，初始损伤和在加载过程中产生的次生缺陷导致其发生破坏；

②微元体符合尺寸二重性要求，即宏观上充分小，可视作连续损伤力学中的质点；细观上充分大，足够包含相应微缺陷。则细观上微元体在破坏前服从胡克定律，但破坏后丧失承载能力；

③微元弹性体强度服从Weibull统计分布，相应的概率密度函数为

(4)

式中：F为表征微元体强度的分布变量；m、F0为反映岩石材料力学性质的Weibull分布参数，m反映岩石脆性，F0则表示岩石的宏观平均强度；P(F)是岩石强度为F时微元体的破坏概率密度函数。

冲击荷载作用下不断增长的破坏微元体数目是岩石发生破坏的主要原因，基于损伤力学理论，定义统计损伤变量D如下：

(5)

式中：n为已破坏的微元数目；N为岩石材料中总微元数目。

在任意区间[F,F+dF]内发生破坏的微元体数目为NP(x)dx，当冲击载荷为F，即x∈[0,F]时，对应的破坏微元数目为

(6)

联立式(5)与式(6)，由微元体破坏概率定义统计损伤变量D可得岩石在外载荷作用下的统计损伤演化方程：

(7)

由式(7)可知，统计损伤变量D与微元体强度F呈正比，而岩石强度变化与应力状态的改变密切相关。因此，需要进一步通过表征微元体强度来反映饱水冻结砂岩在冲击载荷下的损伤演化规律。

3.2 微元体强度的表征

基于岩石的破坏准则通式，考虑Drucker-Prager(D-P)破坏准则同时兼顾中间主应力与静水压力的影响，具有参数构成简单、适用于岩石介质等优点[14]，则微元弹性体强度分布变量的表达式可描述为

(8)

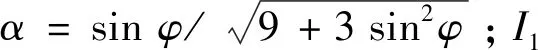
(9)

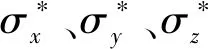
事不宜迟，胖子，你去附近找几个劳力，组织一班人挖树，组织一班人修个通道，三天内我们把树搞出去，我们今年一年的开销就够了，对村民不要说这是什么树，就说树形好，林业部门要依法移植到城市搞绿化，造福更多的人。何泽吩咐道。

根据Lemaitre等效应变假设，即同种有损与无损材料在有效应力作用下产生的应变等价，基本关系式为

{σ*}={σ}/(1-D)=[C]{ε}/(1-D)

(10)

式中：{σ*}为有效应力矢量；{σ}为名义应力矢量；[C]为材料弹性矩阵；{ε}为应变矢量。

鉴于西部白垩系弱胶结砂岩存在大量初始微缺陷，以及各向异性与不均匀性显著的特点，引入初始损伤系数δ(0<δ<1)进行表征，则损伤体有效应力修正表达式为

{σ*}={σ}/(1-δD)=[C]{ε}/(1-δD)

(11)

由式(11)可确定损伤体有效应力与名义应力的关系为

(12)

微元体破坏前服从胡克定律，试样的轴向应变满足下列关系式：

(13)

将式(12)代入式(13)化简得：

(14)

(15)

则式(9)求解得

(16)

岩石材料受单轴冲击时，由于σy=σz=0，则

(17)

微元体强度可表征如下：

(18)

3.3 强度型动态统计损伤本构关系

损伤体Da在发生损伤前处于线弹性状态，根据等效应变原理与式(14)可知三轴条件下损伤体的动态本构关系为

σx=Eεx(1-δD)+μ(σy+σz)

(19)

单轴冲击时，由于σy=σz=0，则

σx=Eεx(1-δD)

(20)

将式(7)、式(18)代入式(20)化简可得单轴冲击条件下损伤体Da的动态本构关系式：

(21)

式(21)即为基于Weibull统计分布、D-P破坏准则及等效应变原理得到的白垩系冻结砂岩强度型动态统计损伤本构关系。

4 本构关系的验证

4.1 基本参数确定

求解上述强度型动态统计损伤本构关系式需要确定εx、E、δ、φ、α、F0、m等7个参数。根据冲击试验获得的应力-应变曲线可知,应变εx用实测数据代入；参数E表示试样初始弹性模量，取应力应变曲线初始上升阶段的斜率；初始损伤系数δ的取值范围为0.95～0.98[16]，可选取不同的δ值进行拟合，根据曲线相关系数R2确定最佳值；内摩擦角φ通过三轴压缩试验确定[18]，-30 ℃时白垩系饱和冻结砂岩内摩擦角φ=31.67°，对应的α=0.17；Weibull分布参数F0和m通过线性回归法拟合确定。

4.2 最佳初始损伤系数

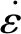
图6 不同δ在不同下的应力应变Fig.6 Stress strain of different δ under different

综合比较可知，选取适当的δ值对理论拟合结果具有显著影响，拟合效果差异主要体现在试样的弹塑性变形阶段，表明δ能够反映白垩系饱和冻结砂岩在动态冲击作用时的弹塑性变形特征。最佳初始损伤系数δ=0.95，理论拟合曲线与试验结果均良好吻合。

4.3 本构模型参数确定

根据确定的参数值，式(21)可进一步化简为适用于本文研究对象的动态本构关系式，其他类型岩石在应用时代入自身相应参数即可：

(22)

表3 模型参数取值Table 3 The value of model parameters

5 结论

1)-30 ℃饱和冻结砂岩动态应力应变曲线可划分为线弹性、弹塑性及塑形软化等3个阶段；动态抗压强度与峰值应变随应变率变化呈指数增长，应变率强化效应显著，砂岩属于率相关性较强材料。

2)裂纹衍生消耗的能量高于裂纹扩展，岩石用于内部微缺陷衍生和扩展的能量随应变率的升高逐渐变大，参与破坏过程的裂隙增多，宏观上表现出动态抗压强度、峰值应变及比能量吸收值的应变率相关性明显。

3)基于微元体强度服从Weibull统计分布假设和连续损伤理论，利用微元体破坏概率定义统计损伤变量D；根据Drucker-Prager破坏准则表征微元体强度分布变量，引入初始损伤系数δ修正损伤体有效应力表达式，推导出强度型动态统计损伤本构关系式。δ能够反映试样在冲击作用时的弹塑性变形特征，最佳初始损伤系数δ=0.95。

4)对比不同应变率下理论拟合曲线与试验实测曲线可知：曲线拟合精度高，引入初始损伤系数δ建立的强度型动态统计损伤本构关系能够较好地反映冲击载荷作用下应力-应变曲线峰前阶段的特征，即线弹性和弹塑性阶段的强度分布。