动载下矿岩-充填体能量传递规律及破坏特性

李祥龙，袁芝斌，王建国，冷智高，段应明，范天林

(1.昆明理工大学国土资源工程学院，昆明 650093;2.云南省中—德蓝色矿山与特殊地下空间开发利用重点实验室，昆明 650093；3.福建马坑矿业股份有限公司，福建 龙岩 364000；4.玉溪矿业有限公司，云南 玉溪 653100)

嗣后充填采矿法是目前地下开采运用较广的采矿方法，在回采矿体时，通常将采区分为矿房和矿柱两个步骤回采，先采矿房，再采矿柱[1]。II步回采矿柱时，在爆破荷载作用下，通常会对两侧充填体造成不同程度的破坏，严重影响回采时的工作安全，而爆破荷载下，矿岩破坏、充填体破坏都涉及复杂的动态力学过程[2]。

对于岩石及矿石的动力学特性，国内外众多学者通过SHPB装置进行了大量研究。李夕兵等[3]研究了动静组合下粉砂岩力学特性；周宗红等[4]通过改良的三维SHPB动静组合加载装置，探讨了白云岩动静组合加载下的应变率效应；李晓峰等[5]利用冲击实验对灰岩、白云岩、砂岩进行了动态力学特性及破裂特征研究；甘德清等[6]分析不同冲击气压下，磁铁矿石破碎能耗特征；王梦想等[7]研究了不同冲击气压下煤岩、泥岩的动态力学性能和破裂破碎特征；刘锦等[8]利用SHPB实验和数值模拟手段研究煤岩动态破坏特征。对于充填体的动力学特性研究，张钦礼等[9-10]通过观察不同应变率下高密度全尾砂胶结充填体破坏特征，来评判高应变率下充填体的稳定性；王建国等[11]通过SHPB冲击实验，对含软夹层的砂浆试件在不同速度下的动态响应、能量传递规律和损伤破坏特性展开研究；曹帅[12]通过不同加载速率下的胶结充填体动力学特性实验，揭示了胶结充填体峰值抗压强度与动力学特性之间的函数关系；Mohamma等[13]通过SHPB实验，对不同配比的混凝土进行了全面分析；朱鹏瑞等[14]研究了不同应变率下的胶结充填体力学特性及其破坏过程机理，并通过数值模拟手段验证了结论的准确性。

对于组合试件的动力学特性研究，杨仁树等[15]利用SHPB实验系统，对波阻抗较大的红砂岩和灰砂岩拼接的复合岩体试样进行不同冲击速度下的冲击实验，研究了复合岩体应力波传播特征、动态应力-应变关系及能力耗散规律；陆菜平等[16-20]都先后对岩-煤-岩组合体进行动力学特性及破坏特性等研究，但是对矿岩-充填体组合试件的动力学分析及能量传递特性方面研究较少。因此矿岩-充填体组合试件的动力学实验分析，对矿柱回采爆破参数优化，及研究爆破应力波对胶结充填体的破坏影响具有重要意义。

1 矿岩-充填体试件冲击实验

1.1 矿岩-充填体组合试件制作

充填体强度主要由水泥含量决定，依据大红山铜矿胶结充填资料，充填体浓度为72%，遂浇筑水泥含量分别为180、250、330 kg/m3的尾砂胶结充填体模型，矿岩选取大红山铜矿东矿段385中段48-54线矿岩，岩性为含铜磁铁变纳质凝灰岩，静力学参数如表1所示。待充填体浇筑完成于自然条件下养护28 d后利用SW-200自动取芯机钻取充填体的芯体及矿岩岩芯，直径为50 mm,长径比建议为1∶1，即矿岩-充填体总高度为50 mm。然后利用SCQ-4A自动切石机切割矿岩与充填体，长度均为25 mm，再在自动双面磨平机上打磨芯体的两个端面，使其不平行度和不垂直度都小于0.02 mm。制作组合试件时，利用环氧树脂将矿岩与胶结充填体进行粘结，制作矿岩-充填体组合试件(后文分别以ZH180、ZH250、ZH330代替)，加工完成试件如图1所示。

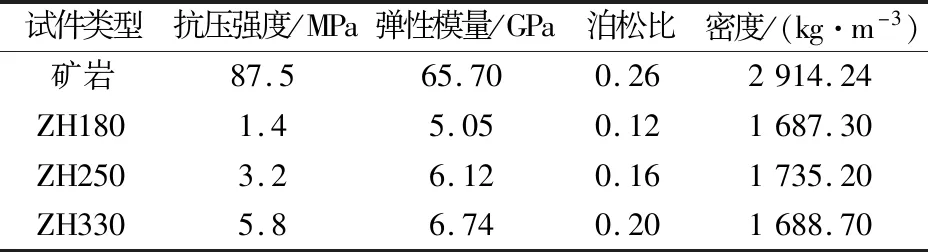
表1 矿岩与充填体静力学参数Table 1 Static parameters of ore rock and backfill

图1 加工完成后组合试件Fig.1 Combine test pieces after processing

1.2 实验设备

实验装置为50 mm的霍普金森动静组合实验系统(见图2)。实验过程中，以组合试件矿岩一端为入射端，组合试件充填体一端为透射端，为保证矿岩-充填体组合试件与加载杆件两端面保持良好接触，在试件两端面涂抹适量黄油[18]。

图2 SHPB实验系统Fig.2 SHPB experimental system

1.3 实验数据处理

(1)

式中：A0为压杆横截面积；E0为压杆系统弹性模量；Ac为组合试件横截面积；L为组合试件长度；C0为压杆中弹性波速；εI(c)为实验测得入射波应变；εR(c)为反射波应变；εT(c)为透射波应变。

根据应力波传播理论和能量守恒定律[22]知：

(2)

式中：WI、WR、WT、WD分别为实验过程的入射能、反射能和透射能以及使试件破坏的吸收能。

WD=WI-WR-WT

(3)

吸收能用于对组合试件做功，致使组合试件内部裂隙扩展直至组合试件破裂，分析不同应变率下，吸能密度，从而更准确表征组合试件能量吸收规律。利用式(4)计算[23]：

(4)

式中：ρ为吸收破碎能密度，也称平均吸能密度，J/cm3；V为组合试件的总体积，cm3。

1.4 实验结果

此次实验分别以0.35、0.40、0.45 MPa冲击气压对组合试件进行冲击实验，实验时以矿岩一端为入射杆端。当冲击气压为0.45 MPa 时，ZH180充填体完全粉碎，分析没有意义，遂剔除。通过对实验系统采集到的其他8组数据，利用式(1)～式(4)计算3种冲击气压下的实验数据，实验结果统计如表2所示。

表2 组合试件冲击试验数据Table 2 Impact test data of combined test piece

2 能量传递规律

2.1 波动性

3种充填体配比组合试件在加载冲击气压下电压与时间变化规律相似，以ZH330原始电压-时间(见图3)进行分析，可以看出在加载气压0.35、0.40、0.45 MPa下，入射波与反射波波峰值不断递增，透射波波峰变化相对较小。在3种加载气压下，ZH330原始波形变化具有一定的相似特征，说明组合试件单轴冲击实验数据具有一定的可靠性。

图3 3种冲击气压下ZH330电压-时间Fig.3 ZH330 voltage-time under 3 kinds of impact air pressure

2.2 能量分配

(5)

式中：WI为入射能；WX为反射能、透射能和吸收能。

由不同应变率下试件能量分配比率(见表3)可以看出，在几组实验中，反射能比率均大于80%，产生这种现象的原因是因为组合试件波阻抗与SHPB杆件波阻抗相差太大，大部分能量以反射波形式消散。

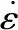
表3 不同应变率下能量分配比率Table 3 Energy distribution ratio under different

2.3 吸能密度与应变率

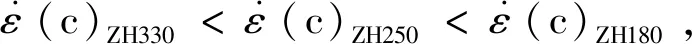
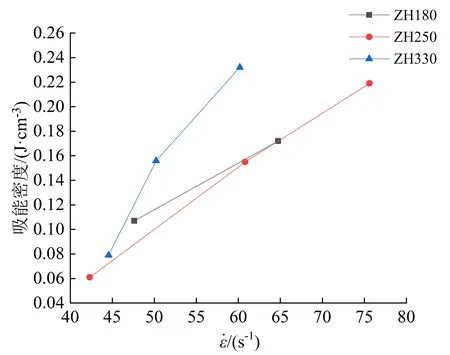
图4 吸能密度与应变率关系Fig.4 Relationship between energy

3 组合试件破坏特性

3.1 破坏形态

图5 组合试件冲击实验效果Fig.5 Effect of combined specimen impact experiment

3.2 充填体破碎平均粒径

为了进一步分析组合试件充填体破坏后粒径分布情况，利用平均粒径ds来表示冲击实验后组合试件充填体破碎程度,计算式如下：

(6)

式中：ds为充填体平均粒径；di为不同孔径下充填体粒径尺寸；ri为粒径为di时，对应粒径质量分数。

对破坏后组合试件充填体碎块度进行粒径筛分，得到不同应变率下充填体碎块筛分质量分数和平均粒径如表4所示。

表4 充填体碎块对应尺寸范围质量分数和平均粒径Table 4 Mass fraction and average particle size of the corresponding size range of the filling body fragments

由平均粒径与应变率关系(见图6)可以看出，随应变率增大，平均粒径减小。同一应变率下平均粒径ds ZH330>ds ZH250>ds ZH180，水泥含量越低，充填体内部尾砂胶结越差，内部孔隙越多，破碎后粒径越小。

图6 平均粒径与应变率关系Fig.6 Relationship between average particle size and

3.3 充填体破碎分形维数

为了更好表征组合试件破坏后充填体粒径分布情况，目前国内外应用较多的是利用分形维数D表示。将统计好的碎块质量-等效边长尺寸按下式进行计算[24]：

D=3-b

(7)

其中，

(8)

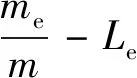
利用式(7)、式(8)，将筛分后不同粒径质量，计算不同配比组合试件充填体在不同应变率下分形维数，计算结果如图7所示。

图7 3种配比块度分形维数与应变率关系Fig.7 Relationship between D and of 3 kinds proportions

由图7可以看出，分形维数随应变率之间具有一定相关性，表现为分形维数随应变率的增加而增加。同等应变率程度下，分形维数DZH180>DZH250>DZH330，而分形维数越大，表示破碎后充填体碎块更多，体积更小[25]，说明同等应变率条件下，水泥含量越低，充填体破坏程度越高。

由分形维数与平均粒径关系(见图8)可知，平均粒径增大，分形维数减小。结合图6可以发现，充填体应变率越大，平均粒径越小，分形维数越大，充填体破坏程度越高，粒径小于0.6 mm质量分数越大，粒径大于10 mm质量分数越小；充填体应变率越小，平均粒径越大，分形维数越小，充填体破坏程度越低，粒径小于0.6 mm质量分数越小，粒径大10 mm质量分数越大。而对3种不同水泥含量充填体和矿岩组合试件单轴冲击荷载下可以发现，分形维数与平均粒径关系非常接近，表明分形维数与平均粒径之间关系不受充填体水泥含量影响。

图8 分形维数与平均粒径的关系Fig.8 Relationship between D and average particle size

4 结论

1)不同配比充填体与矿岩组合试件反射能比率均大于80%，大部分能量以反射波形式消散。

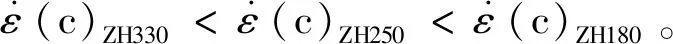
3)由于矿岩充填体强度相差较大，冲击荷载下矿岩破碎形态呈简单块状。充填体破碎情况为，随应变率增加，呈块状分布减少，呈粉末状增多。当应变率在60 s-1左右时，ZH330较ZH250与ZH180相比，充填体破碎形态粉末状明显减少。

4)计算充填体平均粒径与分形维数发现，随应变率增大，平均粒径减小，分形维数增加。同等应变率下平均粒径ds ZH330>ds ZH250>ds ZH180，分形维数DZH180>DZH250>DZH330。