动载下胶结充填体的力学特性试验研究

韩 亮，刘健修

(中国爆破行业协会，北京 100070)

充填采矿法在控制地压、提高回采率以及环境保护方面具有显著的优势，在国内外各大地下矿山的应用日益增加[1-2]。在地下开采中，充填体是维护采场安全，控制围岩移动的关键部分，其处于复杂的应力环境中[3-4]，不仅承受静态荷载，还会受到爆破开挖、地震等造成的冲击荷载(应变率高于10 s-1)。霍普金森压杆(SHPB)是研究材料在高应变率(10～103s-1)下动力学特性的常用设备[5-6]。

自SHPB装置引入岩石动力学特性测试后，国内外学者在岩石动力学领域取得了丰富的成果。CHOCRON S等[7]研究发现大部分岩石的动态抗压强度具有明显的应变率效应，但动态弹性模量，峰值应变等与应变率的关系尚无结论。Frew D J等[8]提出放置薄铜片可以获得近似正弦波，能够确保在冲击过程的持续加载时间内具有恒定的应变速率，随着应变率的增加，石灰岩的抗压强度逐渐增加。许金余等[9]研究了高温后大理岩的冲击力学特性，发现峰值应力、峰值应变均有显著的应变率强化效应，但800 ℃之后，这种强化效应逐渐减弱。刘石等[10]运用分形几何理论对冲击破碎后岩样的破碎块度进行了分析，定量描述了动态抗压强度、能耗密度与分形维数的关系。李夕兵等[11-12]通过混凝土的多次冲击试验得出损伤度与入射能呈指数关系，峰值损伤与龄期呈对数关系降低。龄期7 d以前，混凝土抗冲击荷载能力较差。

相对于岩石、混凝土等强度较大材料的动力学特性研究取得的丰富成果，关于胶结充填体的研究主要集中于静力学，M Fall等[13]从胶凝材料、温度、养护龄期等多种角度探讨了胶结充填体强度的影响因素。杨伟等[14-15]利用SHPB装置测试了充填体的动态力学性能，得到了动态抗压强度与平均应变率之间的关系，但应变率相差较大。因此，笔者通过霍普金森试验系统对冲击载荷作用下充填体动力学特性展开研究，分析动态抗压强度、强度增长因子等力学参数与应变率之间的关系，探讨不同应变率下充填体的变形特征,为矿山开采过程中充填体稳定性研究提供理论依据。

1 充填体动态冲击试验

1.1 SHPB试验装置与原理

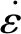
σ(t)=[σI(t)-σR(t)+σT(t)]Ae/(2As)

(1)

(2)

(3)

式中：σI(t)、σR(t)和σT(t)分别为t时刻的入射应力，反射应力和透射应力；Ae为压杆截面积;As为试样截面积;Ls为试样长度。

1.2 充填体试样制备

制备充填体试样的骨料为冀东地区某铁矿全尾砂，水泥为32.5号矿渣硅酸盐水泥，制浆水为自来水。充填料浆的灰砂比为1∶4，质量浓度70%，模具选用规格为φ50×26 mm的自制有机玻璃管模具。所有原料精确称量后倒入JJ-15行星式砂浆搅拌机，将混合物料搅拌均匀，浇筑到自制模具中，24 h后脱模放入标准养护箱(温度20±1 ℃，湿度>90%)养护28 d。达到养护龄期后，对试样两端进行打磨，确保不平整度小于0.02 mm。静态基本物理力学参数如表1所示。

表1 充填体试样物理力学参数Table 1 Physical and mechanical parameters of backfill specimens

1.3 试验方案与结果

由于SHPB试验系统本身的特点，单纯的控制冲击气压得到的冲击速度和应变率跨度太大，因此采取联合调节冲击气压和冲头位置来控制冲击速度小跨度变化。以SHPB系统中冲头能够冲出的最小速度为试验冲击速度最小取值，以导致充填体试样完全碎裂，丧失承载能力并产生粉末的冲击速度为最大速度取值，冲击速度范围约为3～9 m/s，共设计16次充填体试样的冲击试验。每次试验前在充填体两端均匀涂抹黄油，减少端部效应。共得到有效数据16组，试验结果如表2所示。

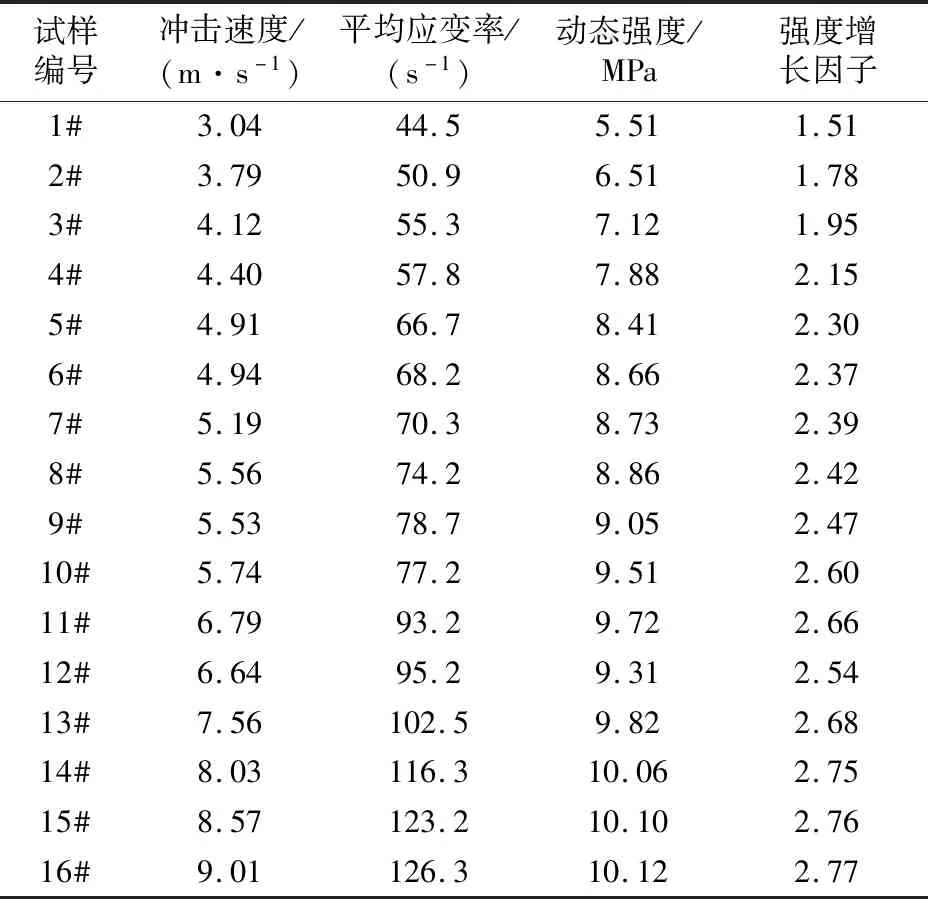
表2 充填体试样冲击压缩试验结果Table 2 Impact compression test results of backfill specimens

2 试验结果分析

2.1 充填体冲击试验典型波形图分析

在霍普金森压杆试验中，应力脉冲信号是通过超动态应变仪对粘贴在压杆表面的动态应变片感应到入射杆和透射杆中的信号进行记录。由6#试样在冲击压缩过程中的典型波形(见图1)可以看出，入射波和反射波方向相反，幅值相近，透射波幅值较小。这是由于充填体试样致密性较差，内部含有大量原始孔隙和微裂隙，波速较低，波阻抗较小。因为试样与压杆之间的波阻抗存在量级上的差异，应力波传播到试样与入射杆接触的界面时，界面前方试样的波阻抗较小，反射波与入射波幅度大小相近，符号相反，透射波很小，表现在波形图上就是透射波幅值很低。通过对波形进行平移，叠加效果如图2所示，试样入射端应力为入射波加反射波，透射端应力为透射波，通过平移叠加可以得到试样两端压杆中应力与时间的关系。从图2中可以看出，叠加波与透射波幅值几乎相等，波形基本重叠，说明充填体试样两端达到了应力平衡[17]。

图1 6#试样所采集到的原始波形Fig.1 Original waveform for specimen 6#

图2 6#试样两端入射杆和透射杆中应力情况Fig.2 Stress on the incident and transmitted bars for specimen 6#

2.2 平均应变率与冲击速度

在SHPB冲击试验中，通过联合调节冲击气压和冲头位置来控制冲击速度，按照试验方案使入射应力和平均应变率均匀的递增。试验过程中最小的冲击速度约为3 m/s，对应的平均应变率为45 s-1左右；最大的冲击速度为9 m/s，对应的平均应变率为130 s-1左右。由平均应变率与冲击速度的关系(见图3)可以看出，平均应变率与冲击速度呈明显的线性正相关。利用线性拟合得到关系式：

图3 平均应变率与冲击速度关系Fig.3 Relationship between average strain rate and impact velocity

(4)

2.3 冲击荷载下充填体试样动态强度特征

由充填体试样动态抗压强度与应变率之间的关系(见图4)可知，当应变率为45 s-1时，试样的动态抗压强度为5.51 MPa，当应变率为126 s-1时，试样动态抗压强度为10.12 MPa。随着应变率的增大，动态强度增加了约84%。引入动态强度增长因子定量表达试样动态抗压强度相对于静态抗压强度的增幅:

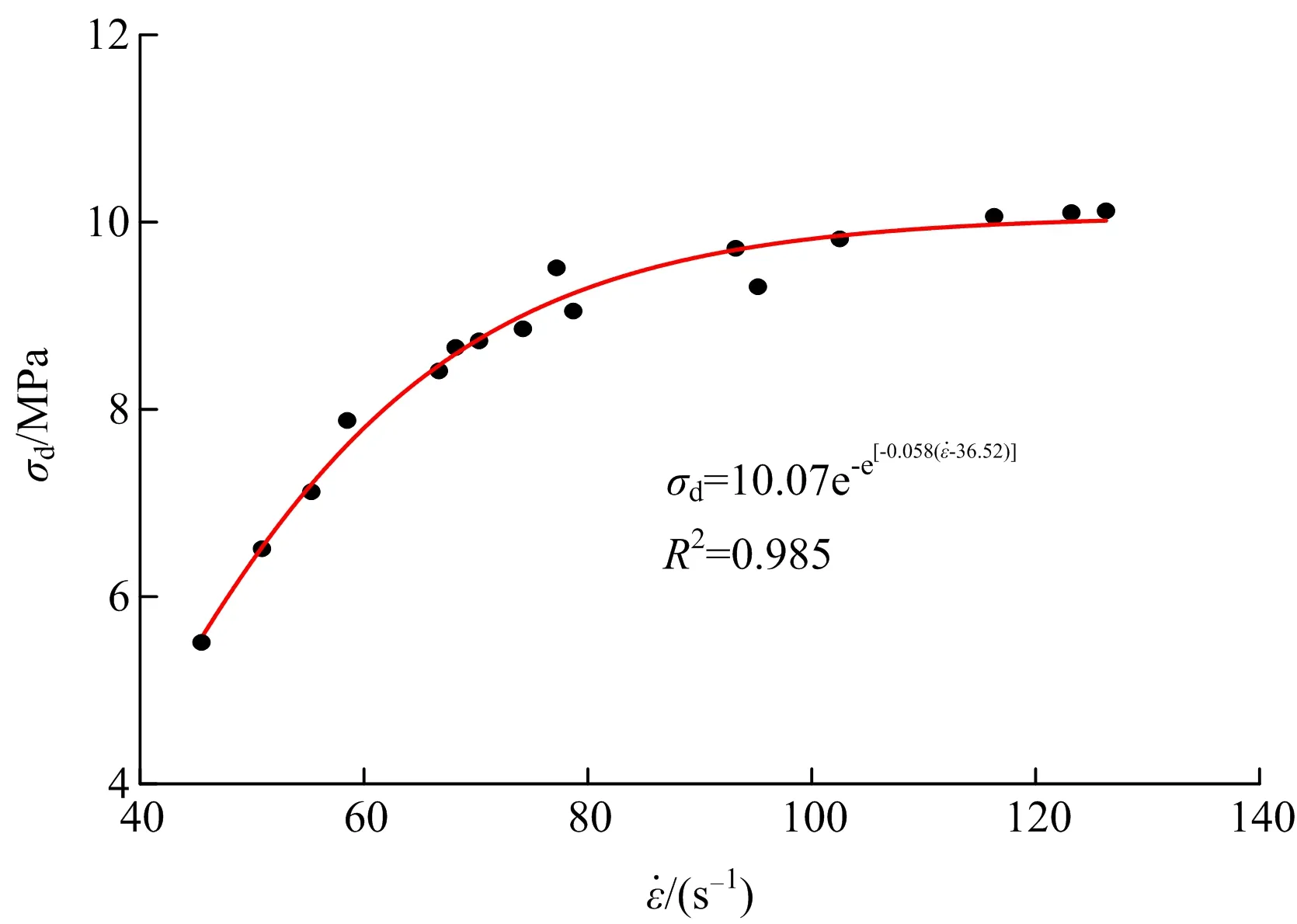
图4 动态抗压强度与平均应变率关系Fig.4 Relationship between dynamic compressive strength and average strain rate

K=σd/σc

(5)

式中：K为动态强度增长因子;σd为动态抗压强度;σc为静态抗压强度。

计算可得充填体动载压缩试验中，当平均应变率范围为45～130 s-1时，K的范围为1.5～3。与其他学者研究结论基本一致。相对于岩石动态强度增长因子来说，充填体试样的K值上限略高，这是因为充填体本身是一种强度较低，致密性较差的材料，内部含有大量的原始孔隙和微裂隙。当充填体试样处于静态加载过程时，持续加载时间充足，原始缺陷充分发育形成贯通面进而大幅度降低了充填体自身承载能力，所表现出的静载抗压强度较低；在动荷载加载过程中，冲击速度较大，冲击荷载作用时间又极短，试样本身没有足够的时间积累能量，根据功能原理，可以依靠提高应力来抵消部分入射能，因此试样的动态强度随平均应变率的提高而增大。

从图4中看出，当应变率小于80 s-1时，试样的动态强度增速较快，应变率从45 s-1到78 s-1，增加了73%，强度从5.51 MPa到9.51 MPa，增幅也达到了73%；当应变率大于80 s-1时，试样的动态抗压强度增长幅度较小，趋于平稳，应变率从80 s-1到126 s-1，增加了58%，动态抗压强度从9.51 MPa增加到10.12 MPa，增幅仅为6%。从试样动态强度增幅与平均应变率增幅的关系可知，当应变率小于80 s-1时，充填体试样的应变率效应明显，当应变率大于80 s-1时，充填体试样基本达到冲击荷载的承载极限，动态强度趋于平稳。引入Gompertz模型[21]表达充填体动态抗压强度与平均应变率之间的关系，拟合效果良好。

(6)

Gompertz模型最初是一种用于描述S型增长的种群生长模型。在充填体动载试验中，随着应变率的增加充填体动态抗压强度先大幅增加后缓慢变化，这一趋势符合Gompertz模型增长趋势；当应变率从中高应变率范围降低至低应变率范围即充填体静载试验范围内时，充填体静载强度也必将趋于某个抗压强度值，初步认为该段符合Gompertz模型开始的平稳阶段。所以综合认为运用Gompertz模型表达充填体动载强度与平均应变率的变化关系是合理的。

结合其他学者的研究结论使用其他模型对于试验结果进行了拟合(见图5)。

图5 动态抗压强度与平均应变率关系Fig.5 Relationship between dynamic compressive strength and average strain rate

由图5知，若采用线性拟合或指数拟合，效果不佳，并且决定系数只有0.7～0.8左右。若采用多项式拟合，在本次试样的应变率范围内尚可，决定系数也超过了0.9，但是从图形中可以看出，当应变率超过80 s-1以后，动态强度趋于稳定，并没有减小，而采用二项式随着应变率增大，动态强度将会有减小的趋势。同样，当应变率减小时，曲线也将会趋于零，而充填体在静荷载作用下，强度也会趋于某个定值，因此采用多项式拟合，数学关系较符合但与实际情况不符。因此认为采用Gompertz模型能最好的表达动态抗压强度与应变率之间的关系。

3 冲击荷载下充填体试样变形特征分析

由不同应变率下充填体应力应变(见图6)可以看出应力应变大致可以分为3个阶段，线弹性阶段、非线性屈服阶段和破坏阶段。与静载下充填体应力应变曲线明显不同的是动载下应力应变曲线刚开始几乎没有下凹，即没有压密阶段，因为冲击荷载的试验过程非常迅速，整个加载过程以微秒计，充填体试样在几微秒的时间就被压密，因此在应力应变曲线中没有体现出压密段而直接进入线弹性阶段。应力应变曲线中弹性阶段应力与应变基本呈线性关系，试样吸收的能量以应变能的形式积聚在试样内部，平均应变率越高，动态抗压强度越大，弹性阶段表现更加明显。弹性阶段过后，曲线开始偏离直线段，进入屈服阶段，试样内部的原始孔隙和新生裂纹进一步发育，试样内部的损伤不断积累，逐渐达到动态强度极值。随着加载过程的持续，试样内部的微裂纹发育扩展形成贯通面，试样进入破坏阶段，表面产生宏观主裂纹，应变率越高，微裂纹越多，相互交叉连通，导致充填体发生碎裂破坏。

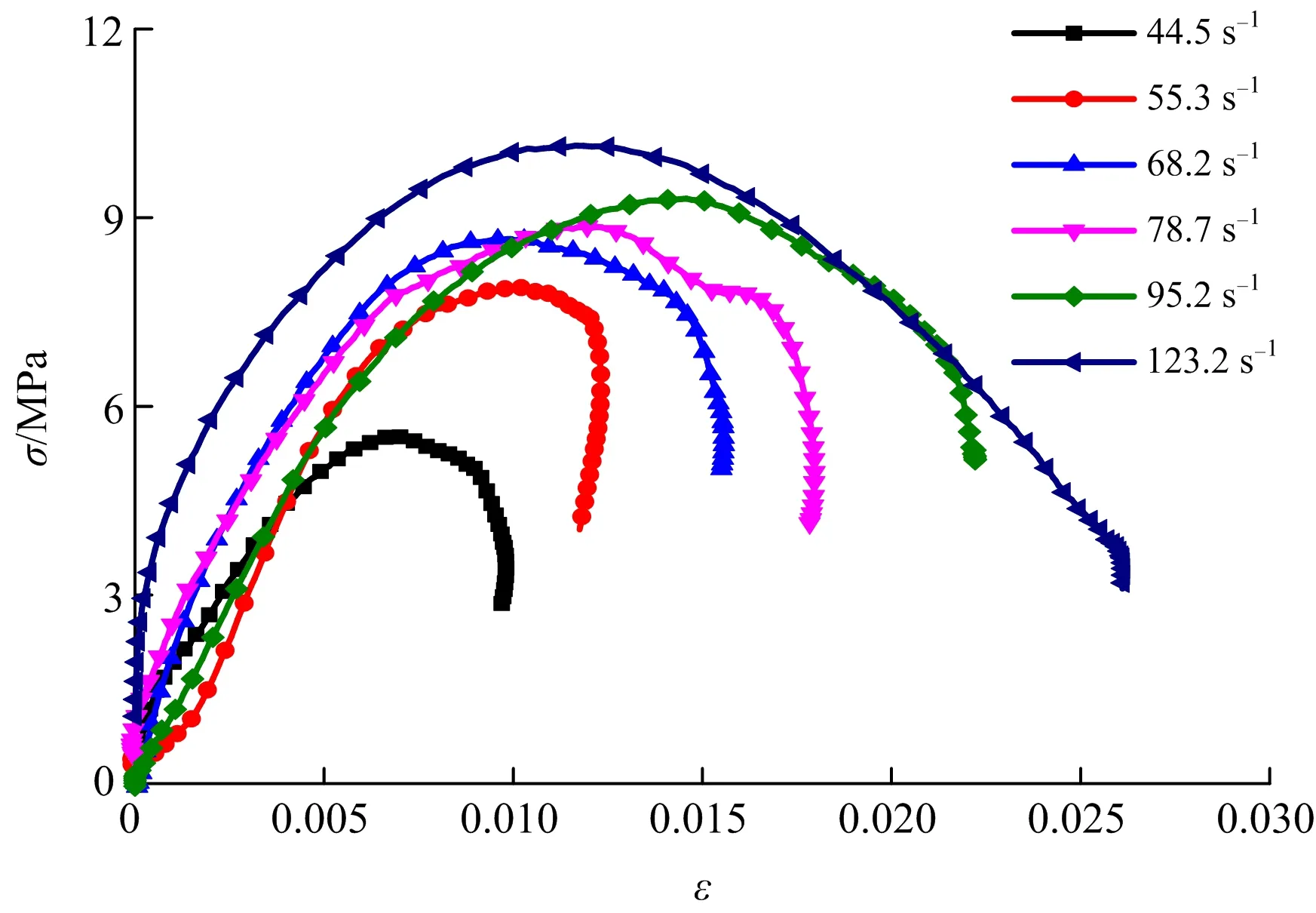
图6 不同应变率下试样的应力应变Fig.6 Stress strain of specimens at different strain rates

从图6可以看出，随着应变率的增加，充填体应力应变曲线的峰后阶段有显著区别。当应变率小于60 s-1，出现“应变回弹”现象，因为在加载过程中充填体内部积聚了一定的弹性能，较低应变率作用下试样内部可能产生了微破裂导致试样失稳，试样整体基本破坏，但仍具有部分承载能力。加载过程中储存在试样内部的弹性应变能使试件没有出现整体破坏，试样仍然具有承载能力，到达试样峰值强度后，应力开始下降，此时积聚在试样内部的弹性能又被释放出来，被压缩的充填体试样恢复形变，应力应变曲线上出现应变回弹现象。

当应变率大于80 s-1时，峰后曲线破坏呈现出“峰后塑性”，充填体试样在外力作用下不断发生变形直至整体丧失承载能力。由于较高的应变率导致加载过程中试样迅速产生大量裂纹并形成宏观破裂面，使试样发生压倒性粉碎破坏，峰前试样内部存储的弹性应变能已经不能使破裂的试样恢复形变，相反弹性应变能的释放加速了裂纹的扩展演化。在外力作用下，应力逐渐减小，应变逐渐增大。

当应变率介于60～80 s-1之间时，峰后曲线类型为“应力跌落”，即应变基本不变，应力迅速跌落；认为是平均应变率处于此范围时，试样已经发生宏观破坏，但还有部分承载能力，加载过程中并没有使试样发生压倒性粉碎破坏，到达峰值强度后，试样产生宏观裂纹，已经无法恢复形变，因此应力迅速跌落至残余强度，应变基本不变[18]。

4 结论

1)在SHPB试样中，通过联合调节冲击气压和冲头位置的方法可以有效控制冲击速度小梯度改变，得到近似等幅变化的平均应变率。

2)胶结充填体动态抗压强度远大于静载强度，当平均应变率范围为45～130 s-1时，动态强度增长因子K的范围为1.5～3；利用Gompertz模型能较好的表达充填体动态抗压强度随平均应变率的增大先迅速增加后趋于稳定的变化趋势。

3)冲击荷载下充填体应力应变曲线的峰后阶段随着平均应变率的增大分为3种类型，当应变率小于60 s-1，表现为“应变回弹”，当应变率大于80 s-1，表现为“峰后塑性”，应变率介于60～80 s-1之间时，表现为“应力跌落”。